人教版数学九年级上册 21.2.2公式法 课件(共20张PPT)
文档属性
| 名称 | 人教版数学九年级上册 21.2.2公式法 课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 431.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 21:13:47 | ||
图片预览








文档简介
(共20张PPT)
人教版数学九年级上册
第二十一章
二元一次方程
21.2.2
公式法
学习目标
1.理解一元二次方程求根公式的推导过程,会用b2-4ac的值判断一元二次方程根的情况,会运用公式法解一元二次方程。
2.通过对求根公式的发现和探索过程,提高观察能力、分析能力和逻辑思维能力。
3.发展独立思考,勇于探索的创新精神,渗透转化思想,使其感受数学的内在美。
同学们,用直接开平方法和配方法解一元二次方程,计算比较麻烦,能否研究出一种更好的方法,迅速求得一元二次方程的实数根呢?
导入新知
你能用配方法解方程
ax2+bx+c=0(a≠0)
吗?
1.化1:
把二次项系数化为1
3.配方:
方程两边都加上一次项系数的一半的平方
2.移项:
把常数项移到方程的右边
4.变形:
方程左边分解因式,右边合并
?
?
?
?
合作探究
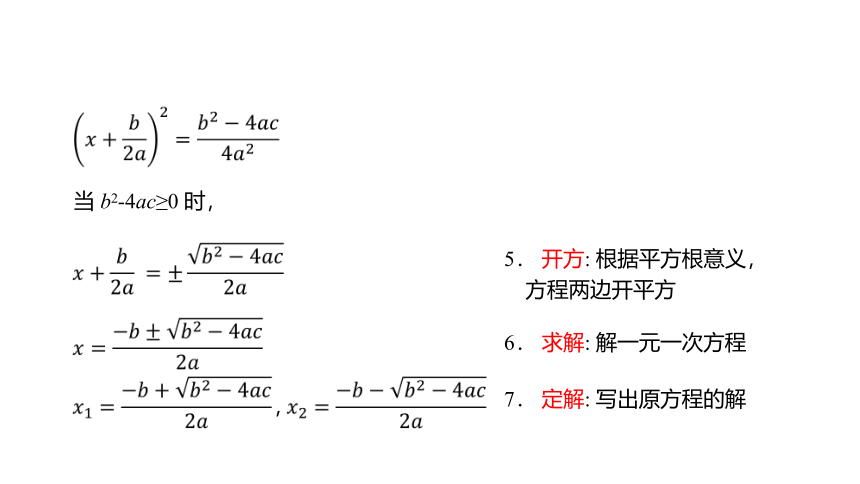
5.
开方:
根据平方根意义,
方程两边开平方
6.
求解:
解一元一次方程
7.
定解:
写出原方程的解
?
当
b2-4ac≥0
时,
?
?
?
?
,
一般地,对于一元二次方程
ax2+bx+c=0(a≠0),
当
b2-4ac≥0
时,它的根是:
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法.
?
用公式法解一元二次方程的前提:
1.
必须化为一般形式的一元二次方程:ax2+bx+c=0(a≠0).
2.
b2?4ac≥0.
一元二次方程
3x2-x=4
中,b2-4ac
的值应是( )
A.49
B.-49
C.47
D.-47
A
典型例题
用公式法解一元二次方程的步骤:
1.整理方程:将方程整理为
ax2+bx+c=0(a≠0)
的形式,找到公式中的
a,b,c,要注意
a,b,c
的符号.
2.计算根的判别式:将
a,b,c
的值代入
Δ=b2-4ac
计算,并判断
Δ
的符号.
3.求根:当
b2-4ac>0
时,方程有两个不相等的实数根,即
当
b2-4ac=0
时,方程有两个相等的实数根,即
.
当
b2-4ac<0
时,方程无实数根.
?
?
?
, .
合作探究
注意:使用公式法时,必须先将一元二次方程化成一般形式,再确定根的判别式非负,最后才能代入求根公式.
例
用公式法解方程:
?
(1)a=1,b=-4,c=-7.
Δ=b2-4ac=(-4)2-4×1×(-7)=44>0,方程有两个不相等的实数根.
解:
即
1.确定系数
2.计算
Δ
3.代入
4.定根
?
?
?
?
,
.
.
例
用公式法解方程:
?
?
解:
.
?
例
用公式法解方程:
(3)方程化为5x2-4x-1=0.
a=5,b=-4,c=-1.
Δ=b2-4ac=(-4)2-4×5×(-1)=36>0.
方程有两个不相等的实数根,
即
,
.
解:
?
?
?
.
?
例
用公式法解方程:
(4)方程化为x2-8x+17=0.
a=1,b=-8,c=17.
Δ=b2-4ac=(-8)2-4×1×17=-4<0.
方程无实数根.
解:
?
用公式法解方程
3x2+5x+1=0,正确的是(
)
?
A
典型例题
1.一元二次方程
3x2=4-2x
的解是
.
?
?
,
解:化为一般式为3x2+2x-4=0,
则
b2-4ac=4-4×3×(-4)=52>0,
?
?
课堂练习
2.已知
α
是一元二次方程
x2-x-1=0
较大的根,则下列对
α
的值估计正确的是(
)
A.2<α<3
B.
1.5<α<2
C.
1<α<1.5
D.
0<α<1
B
?
?
?
?
故选B.
?
A.2x2+4x+1=0
B.2x2-4x+1=0
C.2x2-4x-1=0
D.2x2+4x-1=0
A
?
4.当
a<0
时,方程x|x|+|x|-x-a=0
的解为
.
?
再
见
人教版数学九年级上册
第二十一章
二元一次方程
21.2.2
公式法
学习目标
1.理解一元二次方程求根公式的推导过程,会用b2-4ac的值判断一元二次方程根的情况,会运用公式法解一元二次方程。
2.通过对求根公式的发现和探索过程,提高观察能力、分析能力和逻辑思维能力。
3.发展独立思考,勇于探索的创新精神,渗透转化思想,使其感受数学的内在美。
同学们,用直接开平方法和配方法解一元二次方程,计算比较麻烦,能否研究出一种更好的方法,迅速求得一元二次方程的实数根呢?
导入新知
你能用配方法解方程
ax2+bx+c=0(a≠0)
吗?
1.化1:
把二次项系数化为1
3.配方:
方程两边都加上一次项系数的一半的平方
2.移项:
把常数项移到方程的右边
4.变形:
方程左边分解因式,右边合并
?
?
?
?
合作探究
5.
开方:
根据平方根意义,
方程两边开平方
6.
求解:
解一元一次方程
7.
定解:
写出原方程的解
?
当
b2-4ac≥0
时,
?
?
?
?
,
一般地,对于一元二次方程
ax2+bx+c=0(a≠0),
当
b2-4ac≥0
时,它的根是:
上面这个式子称为一元二次方程的求根公式.
用求根公式解一元二次方程的方法称为公式法.
?
用公式法解一元二次方程的前提:
1.
必须化为一般形式的一元二次方程:ax2+bx+c=0(a≠0).
2.
b2?4ac≥0.
一元二次方程
3x2-x=4
中,b2-4ac
的值应是( )
A.49
B.-49
C.47
D.-47
A
典型例题
用公式法解一元二次方程的步骤:
1.整理方程:将方程整理为
ax2+bx+c=0(a≠0)
的形式,找到公式中的
a,b,c,要注意
a,b,c
的符号.
2.计算根的判别式:将
a,b,c
的值代入
Δ=b2-4ac
计算,并判断
Δ
的符号.
3.求根:当
b2-4ac>0
时,方程有两个不相等的实数根,即
当
b2-4ac=0
时,方程有两个相等的实数根,即
.
当
b2-4ac<0
时,方程无实数根.
?
?
?
, .
合作探究
注意:使用公式法时,必须先将一元二次方程化成一般形式,再确定根的判别式非负,最后才能代入求根公式.
例
用公式法解方程:
?
(1)a=1,b=-4,c=-7.
Δ=b2-4ac=(-4)2-4×1×(-7)=44>0,方程有两个不相等的实数根.
解:
即
1.确定系数
2.计算
Δ
3.代入
4.定根
?
?
?
?
,
.
.
例
用公式法解方程:
?
?
解:
.
?
例
用公式法解方程:
(3)方程化为5x2-4x-1=0.
a=5,b=-4,c=-1.
Δ=b2-4ac=(-4)2-4×5×(-1)=36>0.
方程有两个不相等的实数根,
即
,
.
解:
?
?
?
.
?
例
用公式法解方程:
(4)方程化为x2-8x+17=0.
a=1,b=-8,c=17.
Δ=b2-4ac=(-8)2-4×1×17=-4<0.
方程无实数根.
解:
?
用公式法解方程
3x2+5x+1=0,正确的是(
)
?
A
典型例题
1.一元二次方程
3x2=4-2x
的解是
.
?
?
,
解:化为一般式为3x2+2x-4=0,
则
b2-4ac=4-4×3×(-4)=52>0,
?
?
课堂练习
2.已知
α
是一元二次方程
x2-x-1=0
较大的根,则下列对
α
的值估计正确的是(
)
A.2<α<3
B.
1.5<α<2
C.
1<α<1.5
D.
0<α<1
B
?
?
?
?
故选B.
?
A.2x2+4x+1=0
B.2x2-4x+1=0
C.2x2-4x-1=0
D.2x2+4x-1=0
A
?
4.当
a<0
时,方程x|x|+|x|-x-a=0
的解为
.
?
再
见
同课章节目录
