初中数学最值问题19大模型(pdf版)
图片预览

文档简介
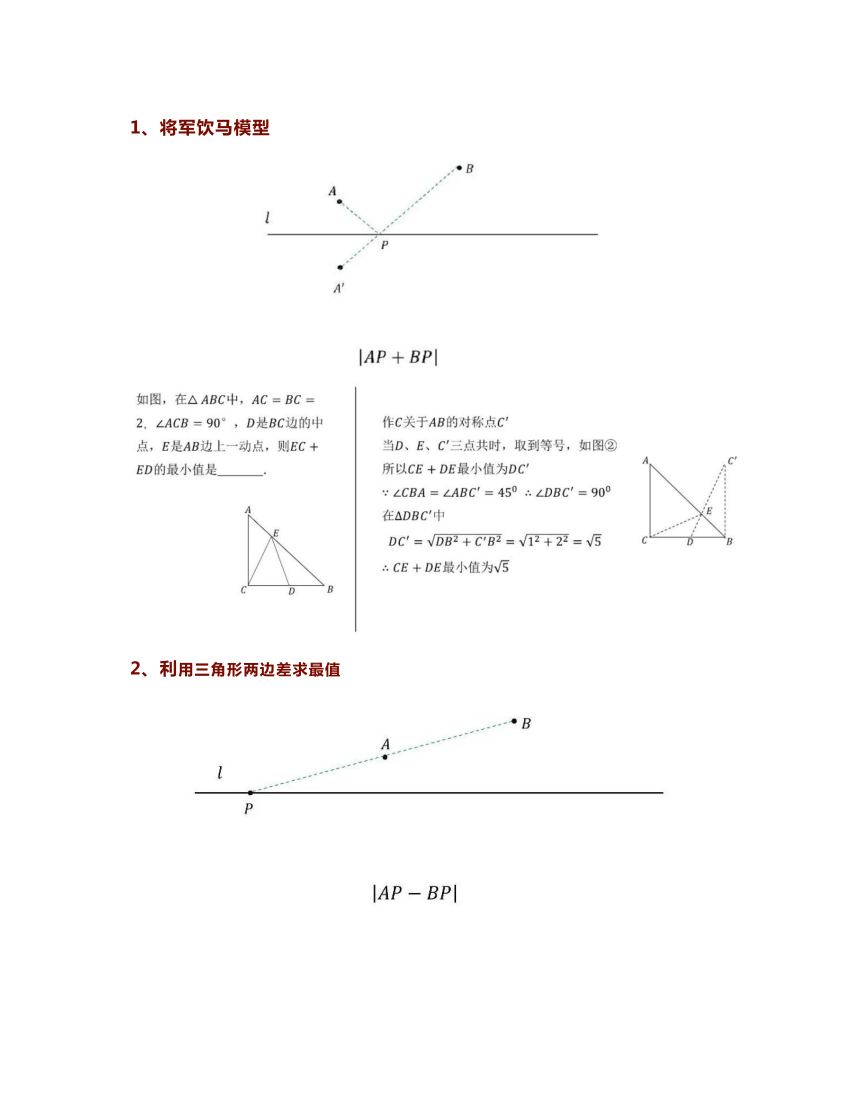
将军饮马模
lAP+BP
如图,在△ABC中,AC=BC
2.∠ACB=90°,D是BC边的中
作C关于AB的对称点C
点,E是AB边上一动点,则EC+
当D、E、C′三点共时,取到等号,如图②
ED的最小值是
所以CE+DE最小值为D
∠CBA=∠ABC′=450∴∠DBC′=900
DC′=√DB2+C'Bz=√12+22=
CE+DE最小值为y5
A
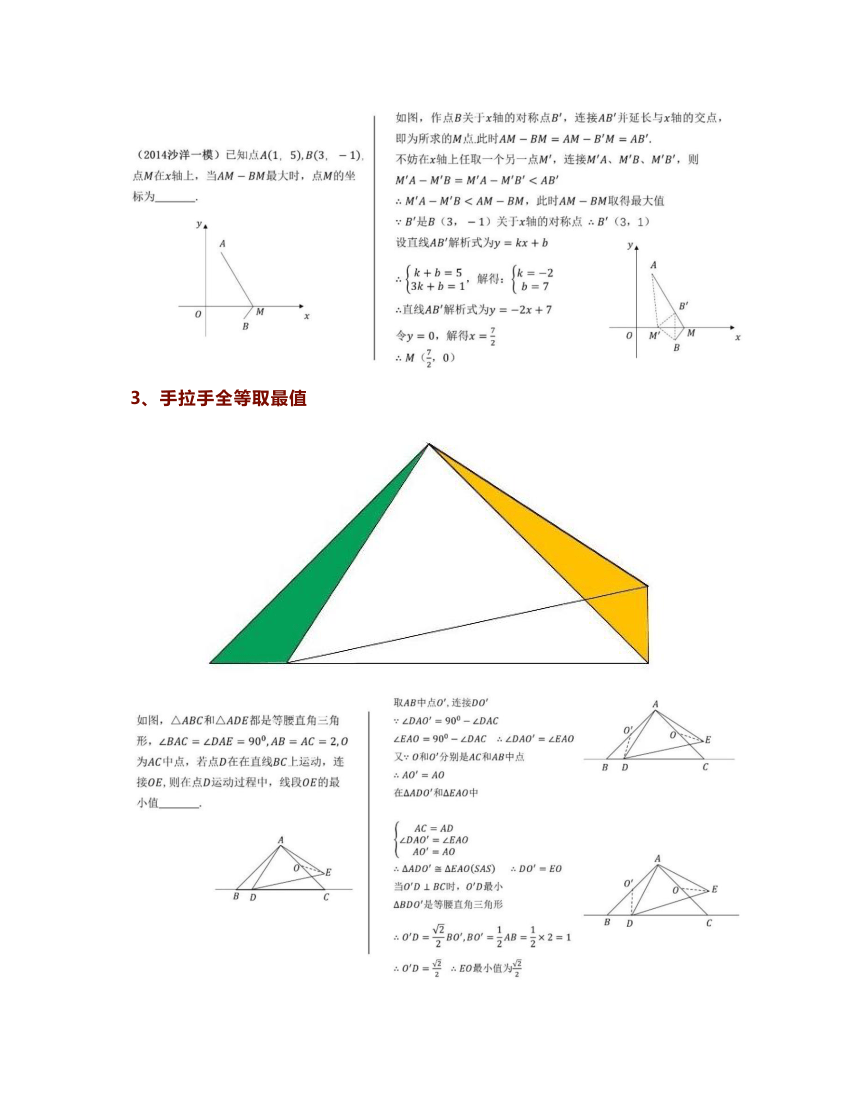
JAP-BP
如图,作点B关于x轴的对称点B,连接AB并延长与x轴的交点
即为所求的M点此时AM
4沙洋一模)已知点A(1,5),B(3,-1)
不妨在x轴上任取一个另一
连接M'A、M'B、M'B',则
点M在x轴上,当AM一BM最大时,点M的坐
M'A-MBEM'A-MB标为
∴M'A-MBB是B(3,-1)关于x轴的对称点∴B’(3,1)
设直线AB解析式为y=kx+b
+b=1,解斜:(=-2
∴直线AB'解析式为y=-2x+7
令y=0,解得x=
取AB中点O,连接D
如图,△ABC和△ADE都是等腰直角三角
形,∠BAC=∠DAE=909,AB=AC=2,O
∠EAO=900-∠DAC∴∠DAO=∠EAO
为AC中点,若点D在在直线BC上运动,连
又:O和O分别是AC和AB中点
接OE,则在点D运动过程中,线段OE的最
在△ADO和△EAO中
△ADO=△EAO(SA):D0mEO
当O'D⊥BC时,O'D最小
oD=¥2B0,BO=1AB
∴.DD
为2
4、手拉手相似取最值
如图,连接CE
如图,△ABC∽△ADE,∠BAC=∠DAE
∵△ABC∽△ADE
90°,AB=6,AC=8,F为DE中点,若
∠ACD=∠AEG
点D在直线BC上运动,连接CF,则在点D
又∵∠AGE=∠DGC
运动过程中,线段CF的最小值是
△AGE∽△DGC
又∵∠AGD=∠EGC
△AGD一△EGC
∠ADG=∠ECG
又∵Rt△ADE中,∠ADG+∠AEG=90°
∠ECG+∠ACD=90°,即∠DCE=90°
F是DE的中点,∴CF=DE,
当AD⊥BC时,AD最短,此时DE最短
当AD⊥BC时,AD=
4.8,
DE
=8,.CF
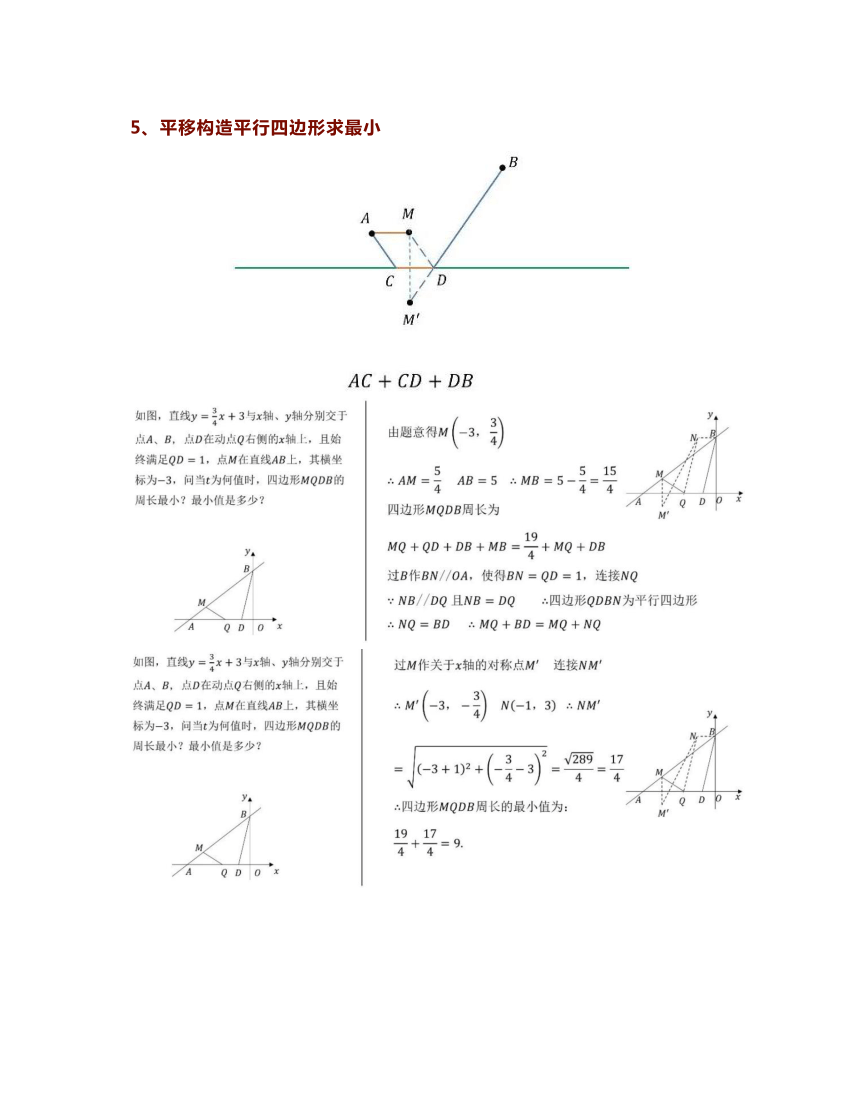
移构造平行四边形求最
AC+CD+
DB
如图,直线y=2x+3与x轴、y轴分别交于
点A、B,点D在动点Q右侧的x轴上,且始
由题意得M(-3,
终满足QD=1,点M在直线AB上,其横坐
为-3,问当t为何值时,四边形MQDB的
AB=5∴MB=5
周长最小?最小值是多少?
四边形MQDB周长为
MQ+QD+DB+
MB
过B作BNOA,使得BN=QD=1,连接NQ
NB/DQ且NB=DQ
边形QDBN为平行四边形
NQ=BD∴MQ+BD=MQ+NQ
如图,直线y=x+3与x轴、y轴分别交于
过M作关于x轴的对称点M连接NM
点A、B,点D在动点Q右侧的x轴上,且始
终满足QD=1,点M在直线AB上,其横坐
M(-3,-d)N(-1,3)NM
标为-3,问当t为何值时,四边形MQDB的
周长最小?最小值是多少
四边形MQDB周长的最小值为
1917
lAP+BP
如图,在△ABC中,AC=BC
2.∠ACB=90°,D是BC边的中
作C关于AB的对称点C
点,E是AB边上一动点,则EC+
当D、E、C′三点共时,取到等号,如图②
ED的最小值是
所以CE+DE最小值为D
∠CBA=∠ABC′=450∴∠DBC′=900
DC′=√DB2+C'Bz=√12+22=
CE+DE最小值为y5
A
JAP-BP
如图,作点B关于x轴的对称点B,连接AB并延长与x轴的交点
即为所求的M点此时AM
4沙洋一模)已知点A(1,5),B(3,-1)
不妨在x轴上任取一个另一
连接M'A、M'B、M'B',则
点M在x轴上,当AM一BM最大时,点M的坐
M'A-MBEM'A-MB
∴M'A-MB
设直线AB解析式为y=kx+b
+b=1,解斜:(=-2
∴直线AB'解析式为y=-2x+7
令y=0,解得x=
取AB中点O,连接D
如图,△ABC和△ADE都是等腰直角三角
形,∠BAC=∠DAE=909,AB=AC=2,O
∠EAO=900-∠DAC∴∠DAO=∠EAO
为AC中点,若点D在在直线BC上运动,连
又:O和O分别是AC和AB中点
接OE,则在点D运动过程中,线段OE的最
在△ADO和△EAO中
△ADO=△EAO(SA):D0mEO
当O'D⊥BC时,O'D最小
oD=¥2B0,BO=1AB
∴.DD
为2
4、手拉手相似取最值
如图,连接CE
如图,△ABC∽△ADE,∠BAC=∠DAE
∵△ABC∽△ADE
90°,AB=6,AC=8,F为DE中点,若
∠ACD=∠AEG
点D在直线BC上运动,连接CF,则在点D
又∵∠AGE=∠DGC
运动过程中,线段CF的最小值是
△AGE∽△DGC
又∵∠AGD=∠EGC
△AGD一△EGC
∠ADG=∠ECG
又∵Rt△ADE中,∠ADG+∠AEG=90°
∠ECG+∠ACD=90°,即∠DCE=90°
F是DE的中点,∴CF=DE,
当AD⊥BC时,AD最短,此时DE最短
当AD⊥BC时,AD=
4.8,
DE
=8,.CF
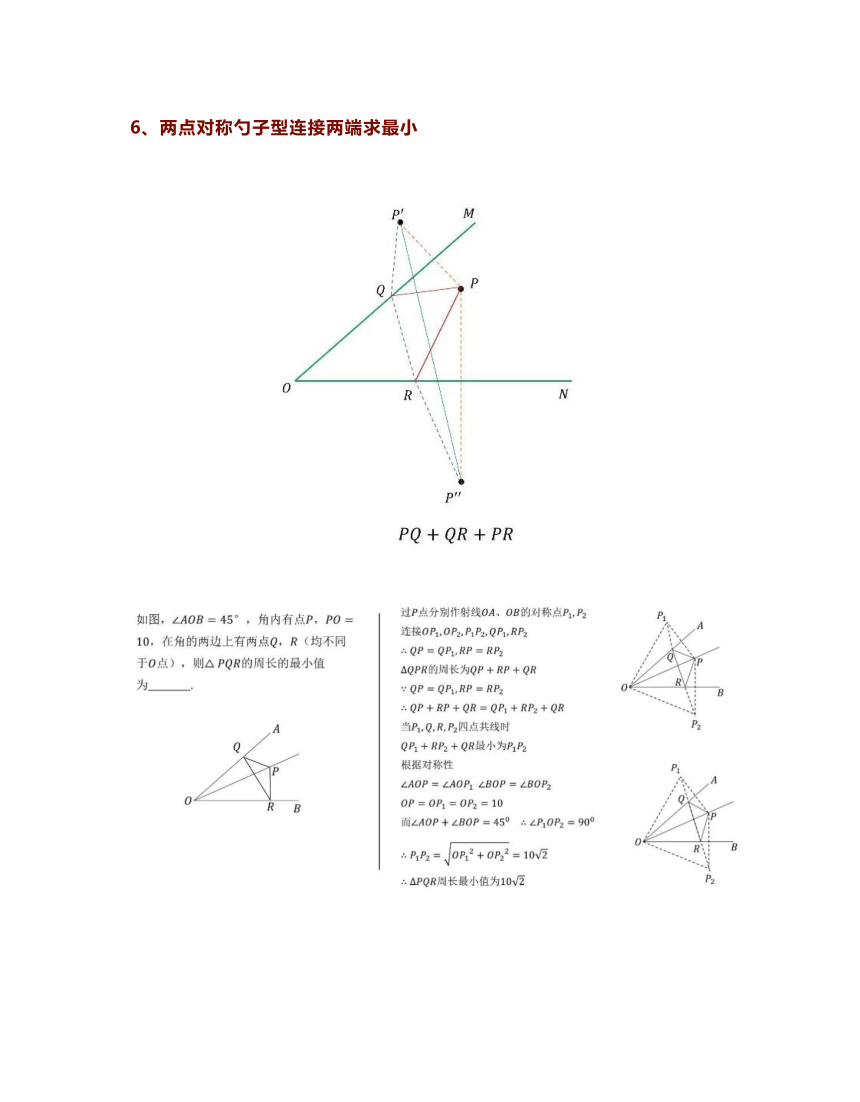
移构造平行四边形求最
AC+CD+
DB
如图,直线y=2x+3与x轴、y轴分别交于
点A、B,点D在动点Q右侧的x轴上,且始
由题意得M(-3,
终满足QD=1,点M在直线AB上,其横坐
为-3,问当t为何值时,四边形MQDB的
AB=5∴MB=5
周长最小?最小值是多少?
四边形MQDB周长为
MQ+QD+DB+
MB
过B作BNOA,使得BN=QD=1,连接NQ
NB/DQ且NB=DQ
边形QDBN为平行四边形
NQ=BD∴MQ+BD=MQ+NQ
如图,直线y=x+3与x轴、y轴分别交于
过M作关于x轴的对称点M连接NM
点A、B,点D在动点Q右侧的x轴上,且始
终满足QD=1,点M在直线AB上,其横坐
M(-3,-d)N(-1,3)NM
标为-3,问当t为何值时,四边形MQDB的
周长最小?最小值是多少
四边形MQDB周长的最小值为
1917
同课章节目录
