初中数学相似三角形模型（pdf版）

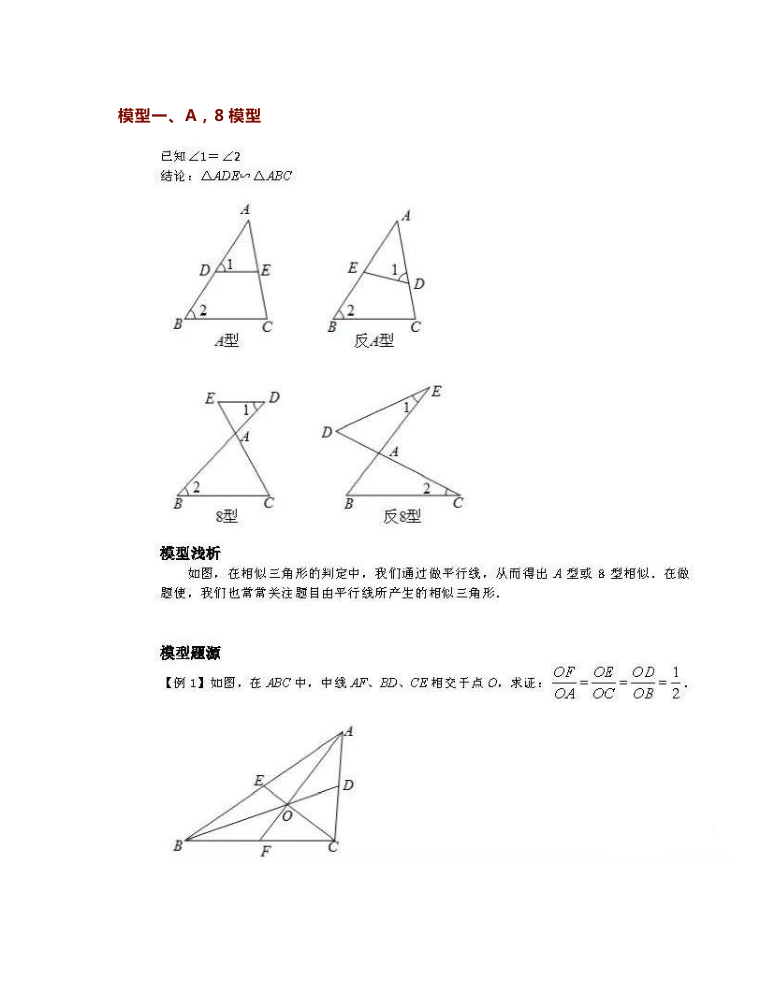
已知∠1=∠2
结论:△ADE∽△ABC
D
理型
反理型
E
反8型
模型浅析
如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.在做
题使,我们也常常关注题目由平行线所产生的相似三角形
棋型题源
OF
O
OD
【例1】如图,在ABC中,中线A、B、CE相交于点O,求证:
OA
OC
B
2
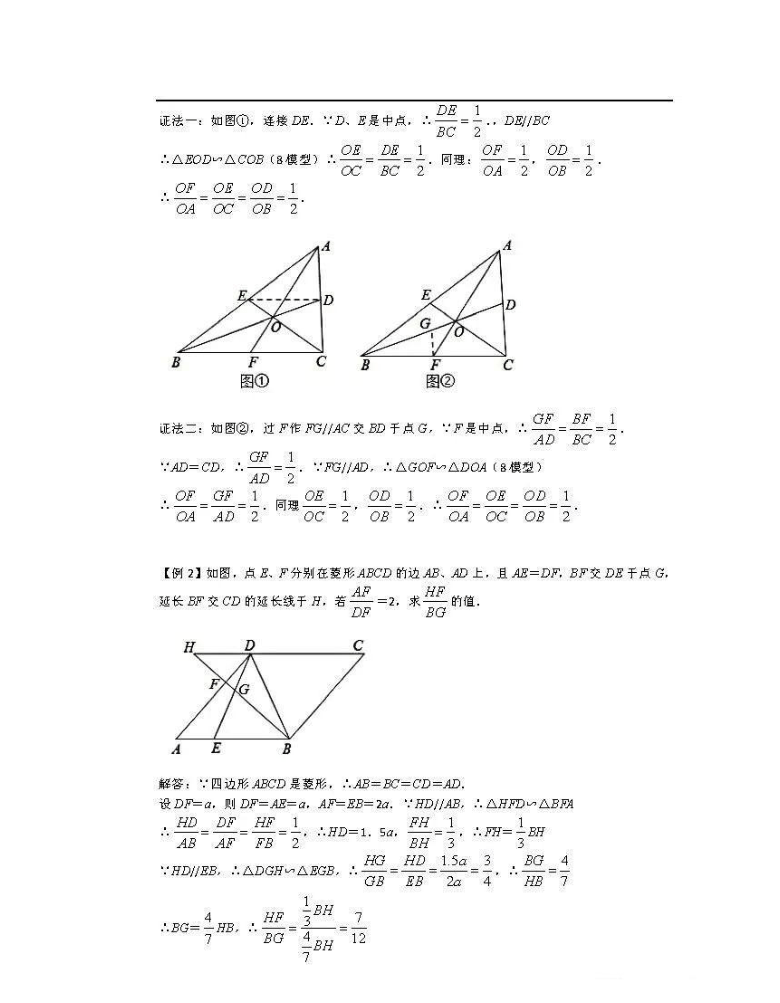
证法一:如图①,连接
∵D、E是中点,∴DE
△BOD△cOB(B模型):E_DE=1,同理:OA2OB=2
OE
OD
DA
CC
OB
D
图①
证法二:如图②,过F作∥A交BD于点G,∵四是中点,:
AD
△GOP∽△DOA〔8模型
OF
GF
1
oD
1
OA
AD
2
同理
oC
2
OB
2
OA
OC
OB
2
【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G,
AF
延长B交CD的延长线于B,若DF=2,求g∈的值
H
解答:∵四边形ABCD是菱形,∴AB=BC=CD=AD.
设DF=a,则
HD
DF
2F
于D/EB,∴△DG∽△BGB,∴一==
-=,
1.如图,D、E分别是△ABC的边AB、BC上的点,且DAC,A、CD相交于点O,若
S△DCg:Sca4=1:25.则SBDE与ScDg的比是
解答::DEAC,∴△DOE△CDA.又50m:8cak=1:12,:D=1
BE
DE
1
BE
1
EC=4,的比是1:4
2.如图所示,在ABCD中,G是BC延长线上的一点,G与BD交于点E,与DC交
点F,此图中的相似三角形共有
对
解:∵四边形ABCD是平行四边形,∴AD/BC,ABCD
〔1)△ABD∽△CDB:(2)△ABE∽△FDE;(3)△AED∽△GEB
4)△ABG∽△FCG∽△FDA,可以组成3对相似三角形,图形中一共有6对相似三角形
3.如图,在△ABC中,中线BD、CE相交于点O,连接AO并延长,交BC于点F,求证
F是BC的中点
D
证明:连接DE交AF于点G,则DE/BC,DE=一BC,∴G为AF中点
B=22=92=B
BF=FC,即点F是BC的中点
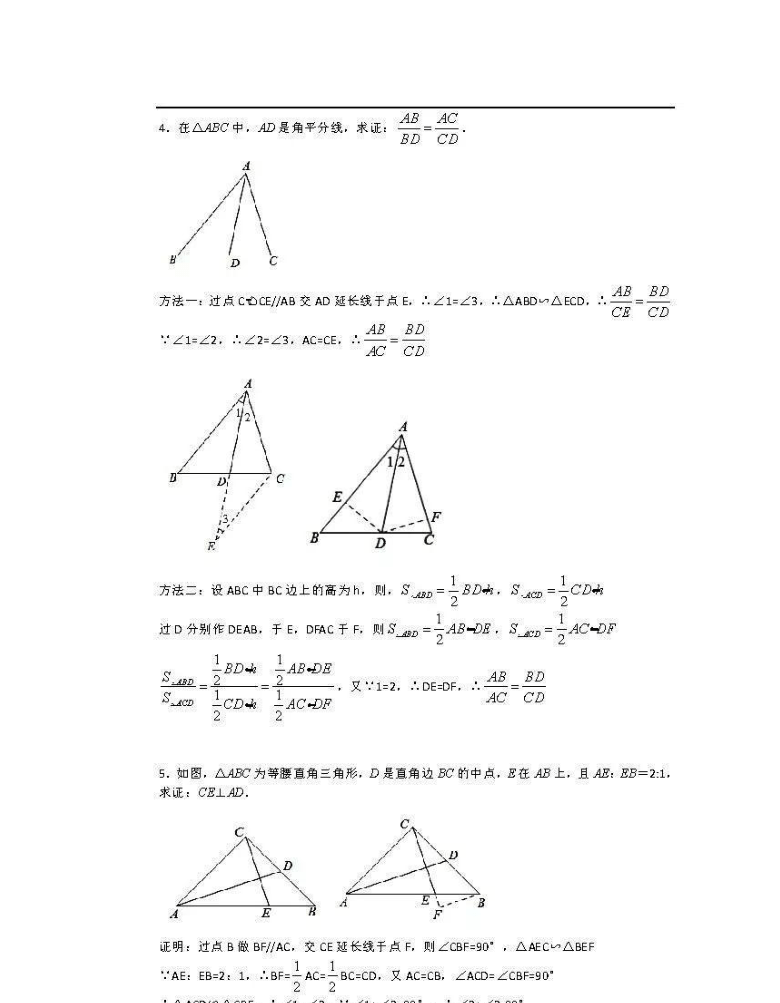
4.在△ABC中,AD是角平分线,求证:AB=出C
BD
CD
方法一:过点CCE/AB交AD延长线于点E,:∠1=∠3,:△ABD∽△ECD.:4B=BD
Ab
BD
∠1=∠2,∴∠2=∠3,AC=CE
A
方法二:设ABC中BC边上的高为h,则,SABD-2
CD中
D分别作0A,干ED除C,则8m0=24B=B,80=4C0F
亠BD
ABcs
E
Ab
BD
S
AACD
AC
CD
5.如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=21,
D
过点B做BFAC,交CE延长线于点F,则
△AC∽△BEF
AE:EB=2:1,∴BF=-AC=-BC=CD,又AC=CB,∠ACD=∠CBF=90°