三角形全等11大解题模型模型总结

平分线模型应用(关注初中数学:
chuzhong-
shuxue
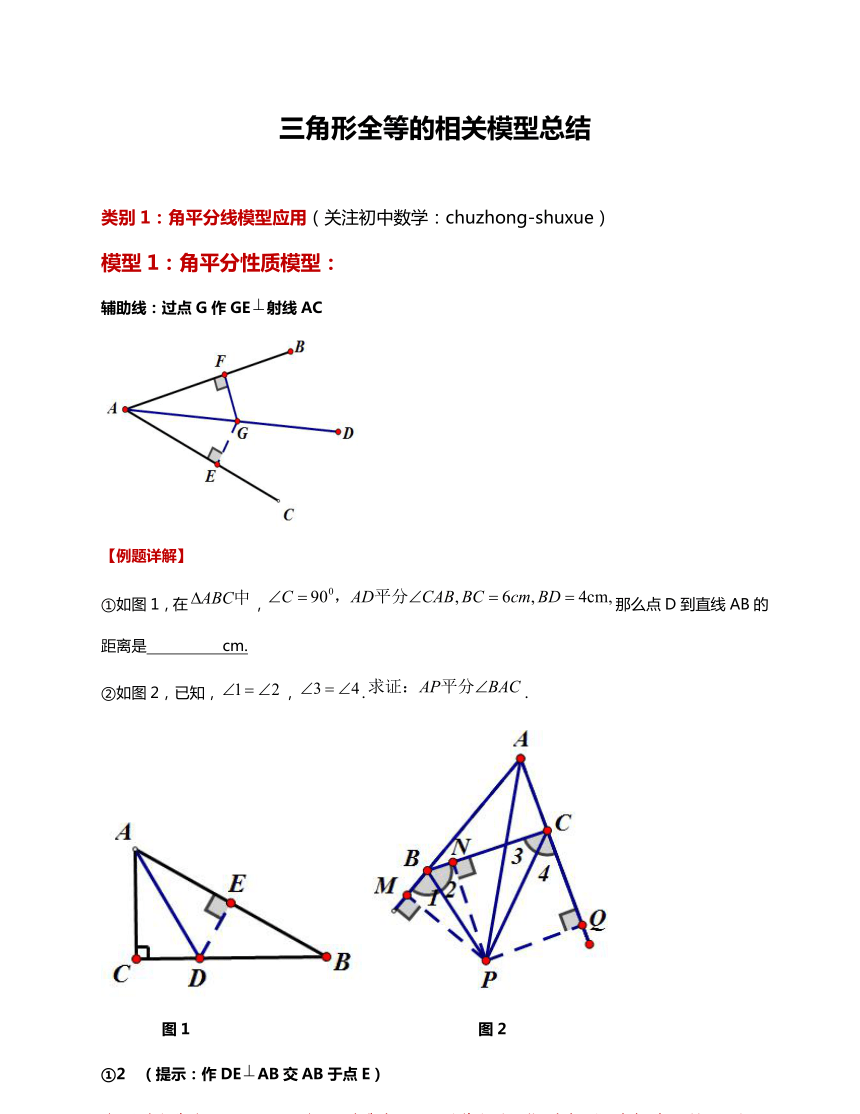
模型1:角平分性厂
线:过点G作
射线AC
①如图
C=90°,AD平分∠C
=4cm,那么点D
线AB的
求
分
C
E
B
A平分∠BAC
C
D
B
B
△ABC
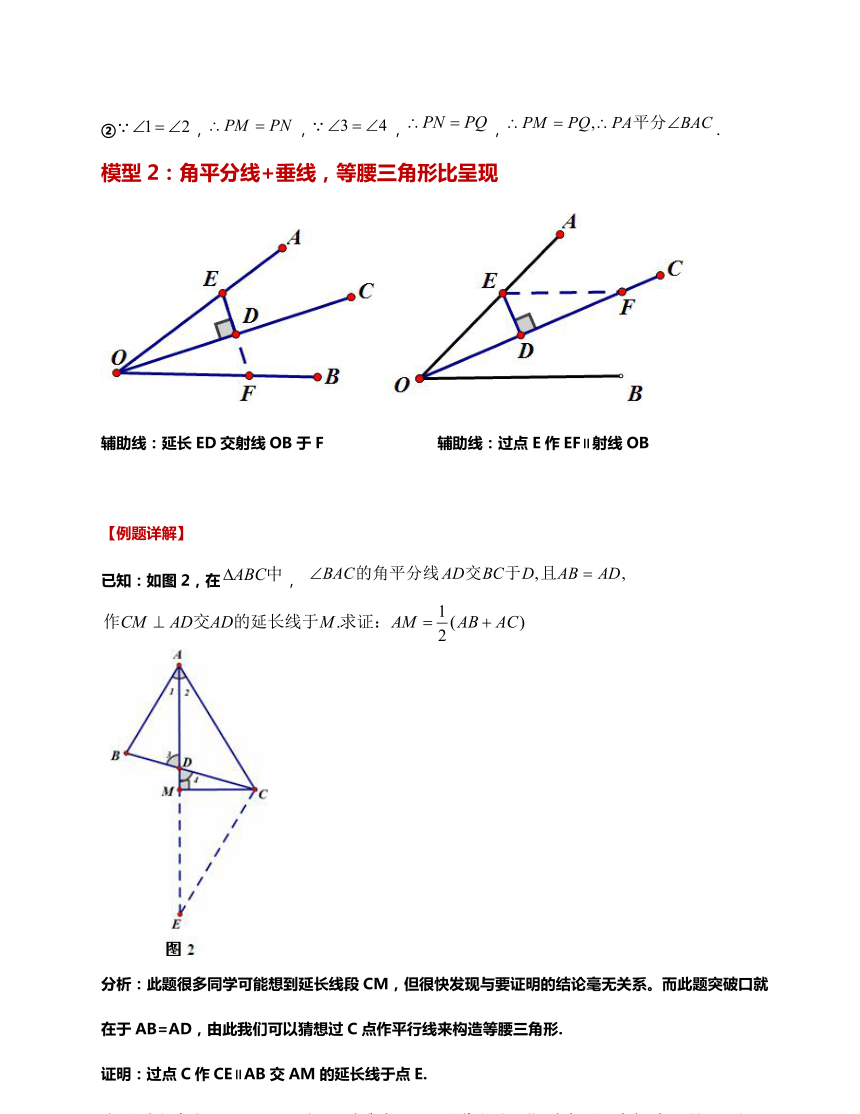
∠BAC的角平分线AD交BC于D
CM⊥AD交AD的延长线于M求证:AM=(AB+AC
线段cM,但很快发现与要证明的结论毫无关系。而此题突破
此我
猜想过C点作平行线来构造等腰三角形
交AM的延长线于点
变形如图,∠1=∠2,B为AC的中点C
于M,A
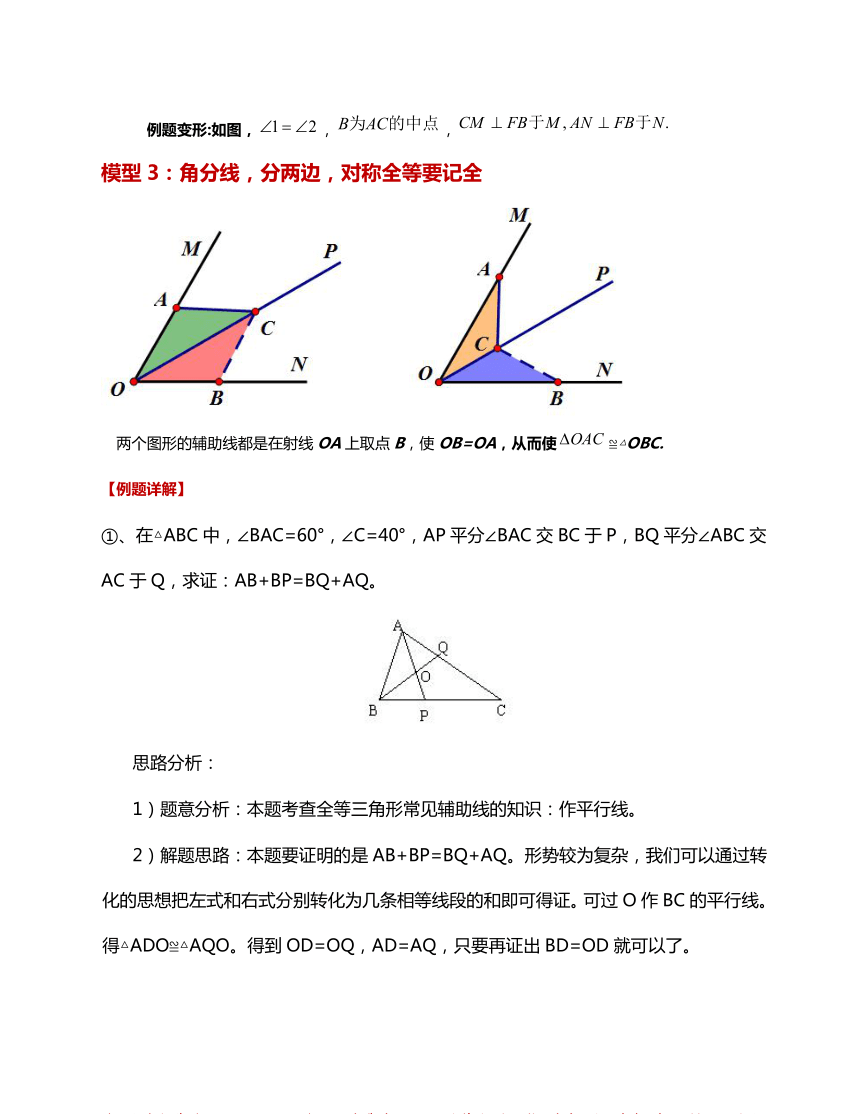
模型3:角分线
对
C
图形的辅助线都是在射线OA上取点B,使OB=OA
AC
①、在△ABC
AC于Q,求证:AB+BP
Q
思路
1)题意分析:本题考查全等
彡常见辅助线的知识:作平行线
2)解题思路:本
AB+BP=BQ+AQ。形势较为复杂,我们可以通过转
的思想把左式和右式
为几条相等线段的和即可得
作BC的平行线
得到
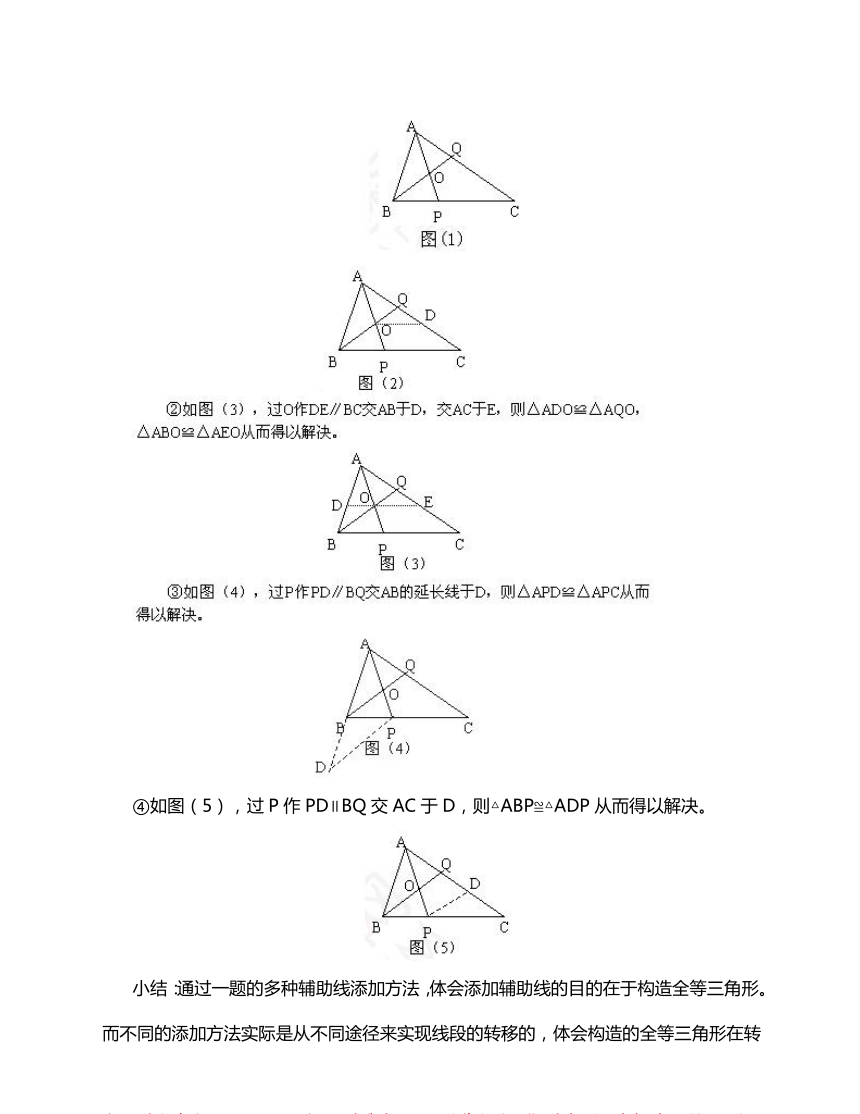
图(1)
②如图(3),过0作DE∥BC交AB于D,交AC于E,则△ADO≌△AQ
△ABO≌△AEO从而得以解决
⑧如图(4),过P作PD∥BQ交AB的延长线于D,则△APD≌△APC从而
得以解决
O“A
图(5
于D,则
而得以解决
B
通过一题的多种辅助线添加方法体会添加辅助线的目的在于构造全等三角形
不同的添加方法实防
途径来实现线段的转移的,体会构造的全等三角形在转
移线段
用。从变换的观点可以看到,不论是作平行线还是倍长中线
乍了一个以中点为旋转中心的旋转变换构造了全等
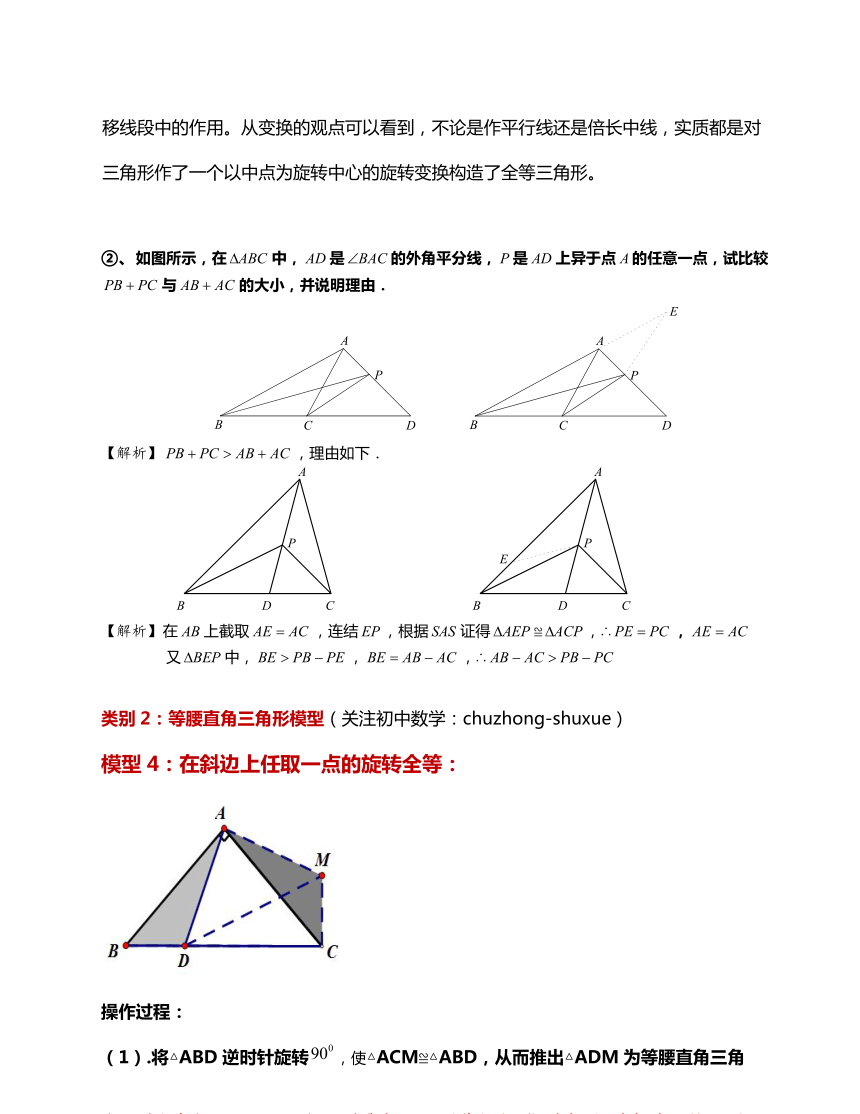
如图所示,在AABC中,AD是∠BAC的外角平分线,P是AD上异于点A的任意一点
并
解析
C>AB+Ac
AB上截取AE=AC
AS证得△AE
△B
AC
类
关注初中数学
模型4
边上任取一点的旋转全
B
C
逆时针旋
从而推出△ADM为等
)过点C作
点是斜边中点,动点在两直角边上滚动的旋转全等
B
C
).使
导
在等腰直角△ABC中,∠BC=90°,点M.N在斜边BC上滑动,且∠MAN=4
是探究BM、MN、CN之间的数量关系
MC⊥BC
过点B作NBBC使NB=CN连AN
解析疔法一过点
使MC=BM连AM
结论:BM2CN2=MN2
2两个全等的含30°,609角的三角板ADE和三角板ABC,如图所示放置
E、A、C三点在一亲直线上,连接BD,取BD的中点M,连接ME,
MC.是判断△EMC的形状,并证明你的结论
法一:连接AM,证明4
MDEA
MAC特别注意证明∠MDE=∠MAC
方法
点M作
点N,得出MN为直角梯形的中位线,从而导b
MEC为等腰
形