立体几何解题中的转化策略
图片预览

文档简介
(共21张PPT)
立体几何解题中的转化策略
数学必修2第一章专题复习之一
位置关系的证明
直观图与展开图
平行关系的转化
垂直关系的转化
垂直与平行关系的转化
角 度
线线角、线面角和二面角
长 度、表面积与体积
直观图与三视图
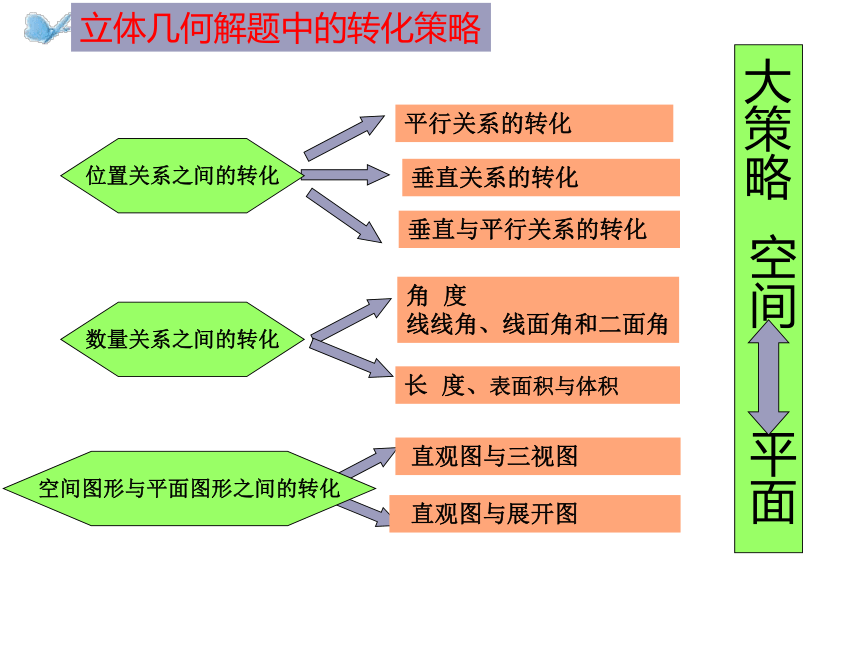
位置关系之间的转化
数量关系之间的转化
空间图形与平面图形之间的转化
大策略
空间
平面
立体几何解题中的转化策略
大策略:空间 平面
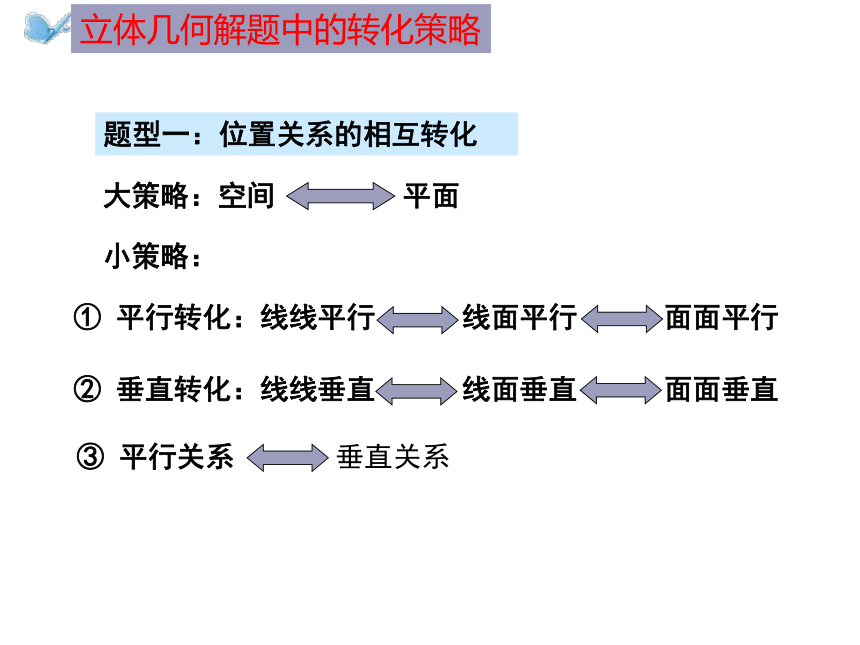
题型一:位置关系的相互转化
小策略:
③ 平行关系 垂直关系
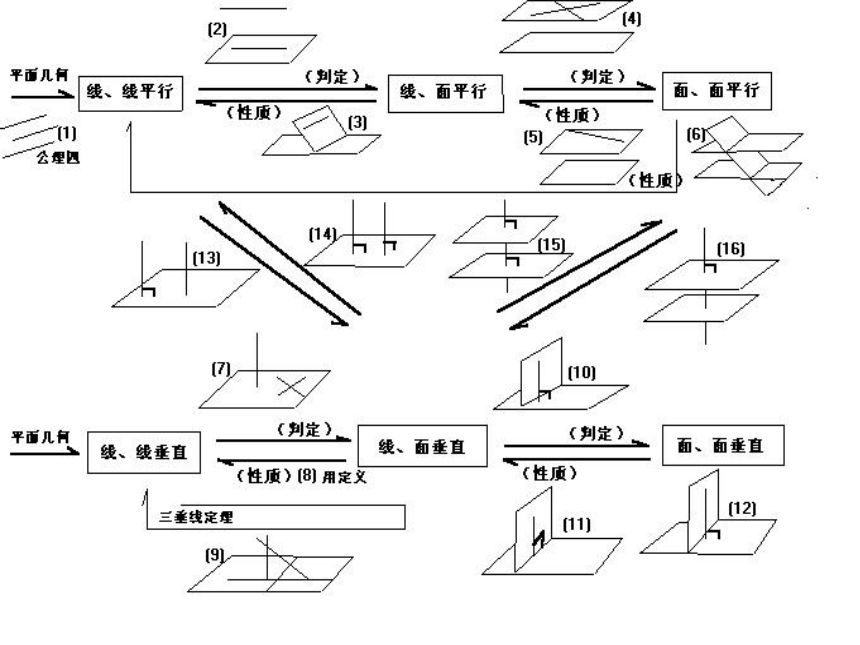
① 平行转化:线线平行 线面平行 面面平行
② 垂直转化:线线垂直 线面垂直 面面垂直
立体几何解题中的转化策略
题型一:位置关系的相互转化
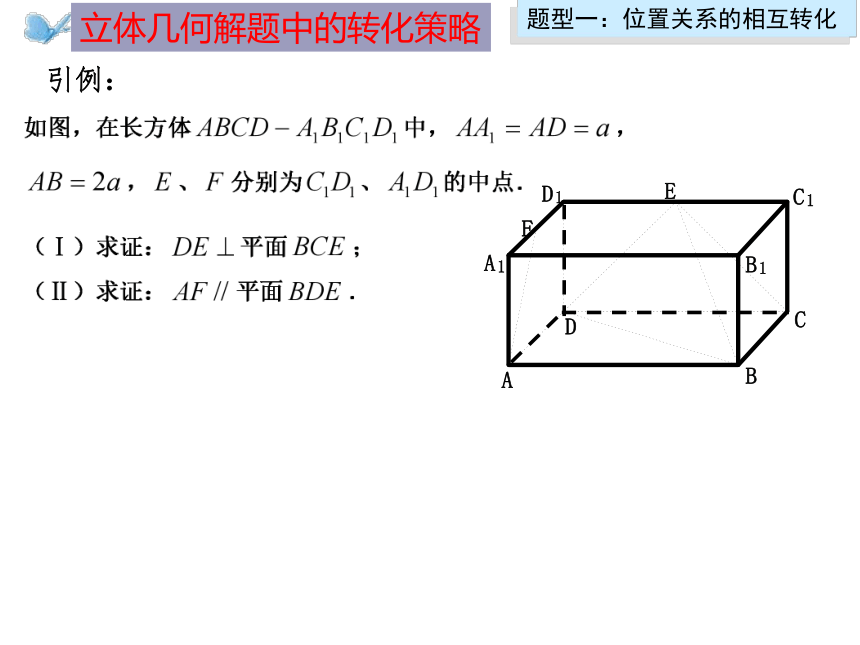
引例:
立体几何解题中的转化策略
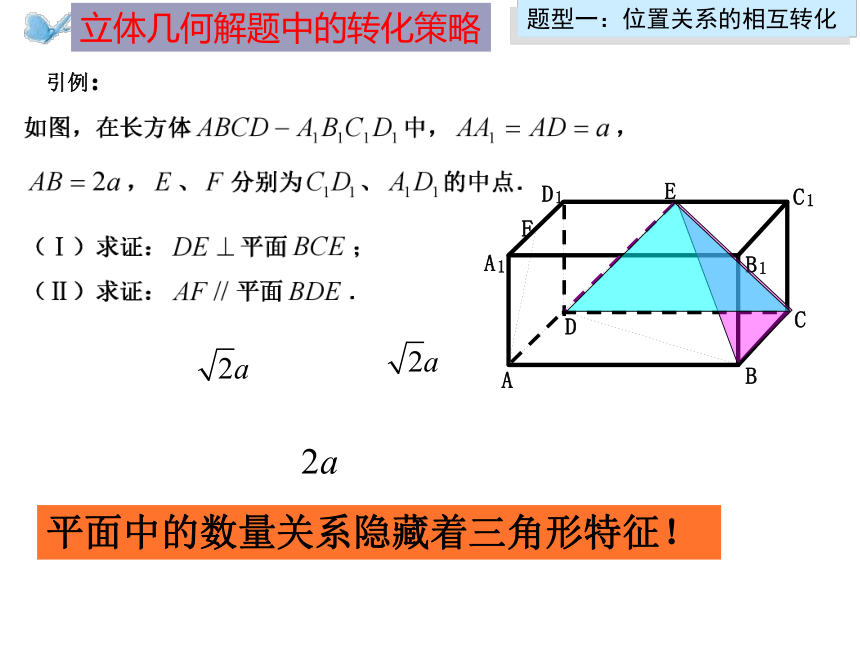
平面中的数量关系隐藏着三角形特征!
题型一:位置关系的相互转化
引例:
立体几何解题中的转化策略
立体几何解题中的转化策略
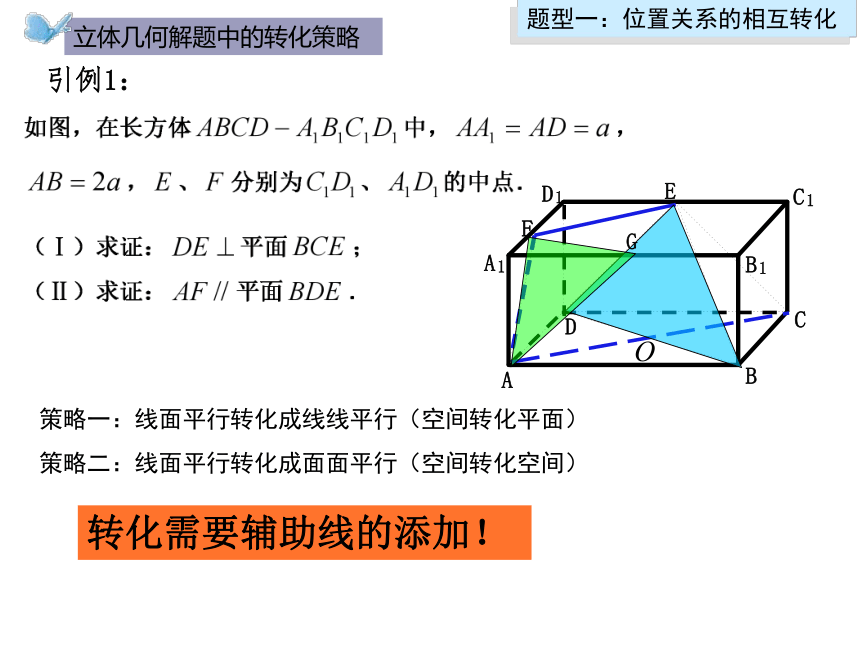
转化需要辅助线的添加!
题型一:位置关系的相互转化
引例1:
策略一:线面平行转化成线线平行(空间转化平面)
策略二:线面平行转化成面面平行(空间转化空间)
G
立体几何作辅助线的
一般思路和常用方法
做立体几何题,性质定理是打开解题思路的关键,也是引入辅助线的基础,它可告诉我们应该如何作辅助线,其中最常用的是线面平行和面面垂直性质定理。
立体几何解题中的转化策略
题型一:位置关系的相互转化
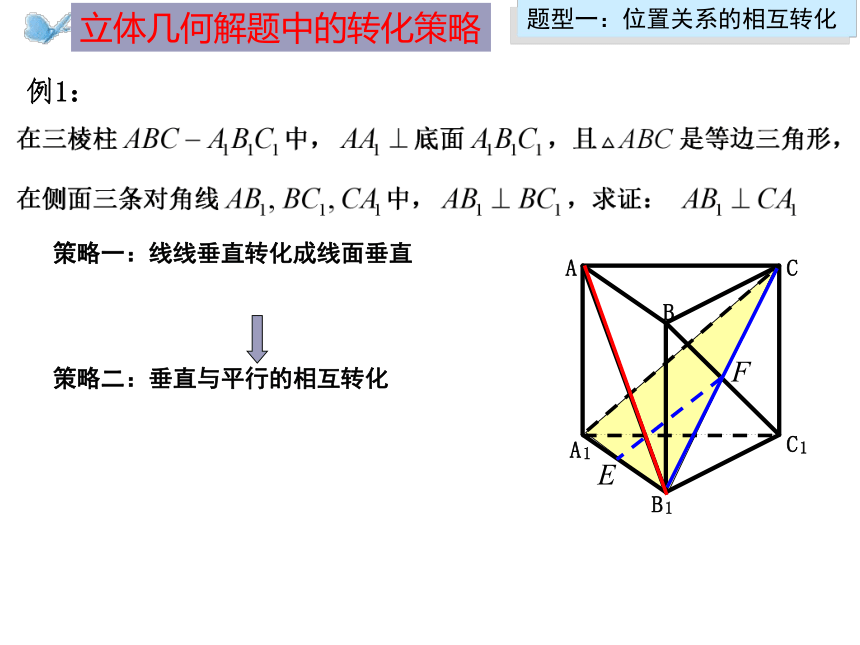
例1:
策略一:线线垂直转化成线面垂直
策略二:垂直与平行的相互转化
立体几何解题中的转化策略
题型一:位置关系的相互转化
例1:
策略一:线线垂直转化成线面垂直
策略二:垂直与平行的相互转化
策略三:线面垂直转化成线线垂直
立体几何解题中的转化策略
关注翻折过程的“变”与“不变”!
立体几何解题中的转化策略
例
2
如图,在矩形
中,
,
,沿对角线
把
折起,使
移到
点,过点
作
^
平面
,垂足
恰好在
上
(
1
)求证:
;
(
2
)求证:
;
关注翻折过程的“变”与“不变”!
立体几何解题中的转化策略
例
2
如图,在矩形
中,
,
,沿对角线
把
折起,使
移到
点,过点
作
^
平面
,垂足
恰好在
上
(
1
)求证:
;
(
2
)求证:
;
一个多面体的直观图及三视图如图所示:
练习:
(其中
分别是
、
的中点)
正视图
侧视图
俯视图
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
练习:
(其中
分别是
、
的中点)
直三棱柱
(1)求证:
平面
;
策略:利用中位线将线面平行转化成线线平行
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
练习:
(其中
分别是
、
的中点)
直三棱柱
(2)求该多面体的表面积与体积;
(1)求证:
平面
;
(3)求二面角
的正切值;
(4)求多面体
的体积;
(5)求直线
与平面
所成的角.
立体几何解题中的转化策略
课堂小结:
在具体的综合题目中需要综合多种策略并用,
方能在峰回路转中达到题解的目的,
这就是立体几何转化思维的魅力所在!
万变不离其宗,掌握好位置关系之间的转化:
平行关系的转化、
垂直关系的转化、
垂直与平行关系的转化;
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(1)求该多面体的表面积与体积;
策略:空间几何体的相互转化
可考虑将该多面体补图成正方体
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(3)求二面角
的正切值;
策略:将二面角转化成平面角, 先找后求
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(4)求多面体
的体积;
策略:将点面距离转化成点线距离
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(5)求直线
与平面
所成的角.
策略:将线面角转化成线线角,先找后求
解:
立体几何解题中的转化策略
立体几何解题中的转化策略
数学必修2第一章专题复习之一
位置关系的证明
直观图与展开图
平行关系的转化
垂直关系的转化
垂直与平行关系的转化
角 度
线线角、线面角和二面角
长 度、表面积与体积
直观图与三视图
位置关系之间的转化
数量关系之间的转化
空间图形与平面图形之间的转化
大策略
空间
平面
立体几何解题中的转化策略
大策略:空间 平面
题型一:位置关系的相互转化
小策略:
③ 平行关系 垂直关系
① 平行转化:线线平行 线面平行 面面平行
② 垂直转化:线线垂直 线面垂直 面面垂直
立体几何解题中的转化策略
题型一:位置关系的相互转化
引例:
立体几何解题中的转化策略
平面中的数量关系隐藏着三角形特征!
题型一:位置关系的相互转化
引例:
立体几何解题中的转化策略
立体几何解题中的转化策略
转化需要辅助线的添加!
题型一:位置关系的相互转化
引例1:
策略一:线面平行转化成线线平行(空间转化平面)
策略二:线面平行转化成面面平行(空间转化空间)
G
立体几何作辅助线的
一般思路和常用方法
做立体几何题,性质定理是打开解题思路的关键,也是引入辅助线的基础,它可告诉我们应该如何作辅助线,其中最常用的是线面平行和面面垂直性质定理。
立体几何解题中的转化策略
题型一:位置关系的相互转化
例1:
策略一:线线垂直转化成线面垂直
策略二:垂直与平行的相互转化
立体几何解题中的转化策略
题型一:位置关系的相互转化
例1:
策略一:线线垂直转化成线面垂直
策略二:垂直与平行的相互转化
策略三:线面垂直转化成线线垂直
立体几何解题中的转化策略
关注翻折过程的“变”与“不变”!
立体几何解题中的转化策略
例
2
如图,在矩形
中,
,
,沿对角线
把
折起,使
移到
点,过点
作
^
平面
,垂足
恰好在
上
(
1
)求证:
;
(
2
)求证:
;
关注翻折过程的“变”与“不变”!
立体几何解题中的转化策略
例
2
如图,在矩形
中,
,
,沿对角线
把
折起,使
移到
点,过点
作
^
平面
,垂足
恰好在
上
(
1
)求证:
;
(
2
)求证:
;
一个多面体的直观图及三视图如图所示:
练习:
(其中
分别是
、
的中点)
正视图
侧视图
俯视图
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
练习:
(其中
分别是
、
的中点)
直三棱柱
(1)求证:
平面
;
策略:利用中位线将线面平行转化成线线平行
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
练习:
(其中
分别是
、
的中点)
直三棱柱
(2)求该多面体的表面积与体积;
(1)求证:
平面
;
(3)求二面角
的正切值;
(4)求多面体
的体积;
(5)求直线
与平面
所成的角.
立体几何解题中的转化策略
课堂小结:
在具体的综合题目中需要综合多种策略并用,
方能在峰回路转中达到题解的目的,
这就是立体几何转化思维的魅力所在!
万变不离其宗,掌握好位置关系之间的转化:
平行关系的转化、
垂直关系的转化、
垂直与平行关系的转化;
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(1)求该多面体的表面积与体积;
策略:空间几何体的相互转化
可考虑将该多面体补图成正方体
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(3)求二面角
的正切值;
策略:将二面角转化成平面角, 先找后求
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(4)求多面体
的体积;
策略:将点面距离转化成点线距离
解:
立体几何解题中的转化策略
一个多面体的直观图及三视图如图所示:
例3(综合题型):
(其中
分别是
、
的中点)
直三棱柱
(5)求直线
与平面
所成的角.
策略:将线面角转化成线线角,先找后求
解:
立体几何解题中的转化策略
