鲁教版八年级数学上册 5.2 平行四边形的判断 同步练习 (word版 无答案)
文档属性
| 名称 | 鲁教版八年级数学上册 5.2 平行四边形的判断 同步练习 (word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 147.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 21:19:28 | ||
图片预览

文档简介
5.2
平行四边形的判断
同步练习
下列说法正确的是( )
A.
对角线相等的四边形是平行四边形
B.
一组对边平行,另一组对边相等的四边形是平行四边形
C.
一组对边相等,一组对角相等的四边形是平行四边形
D.
一组对边平行且相等的四边形是平行四边形
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,那么阴影部分的面积是平行四边形ABCD面积的(?
?
?
)
A.
B.
C.
D.
如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有(?
?)
?
A.
5对
B.
6对
C.
7对
D.
8对
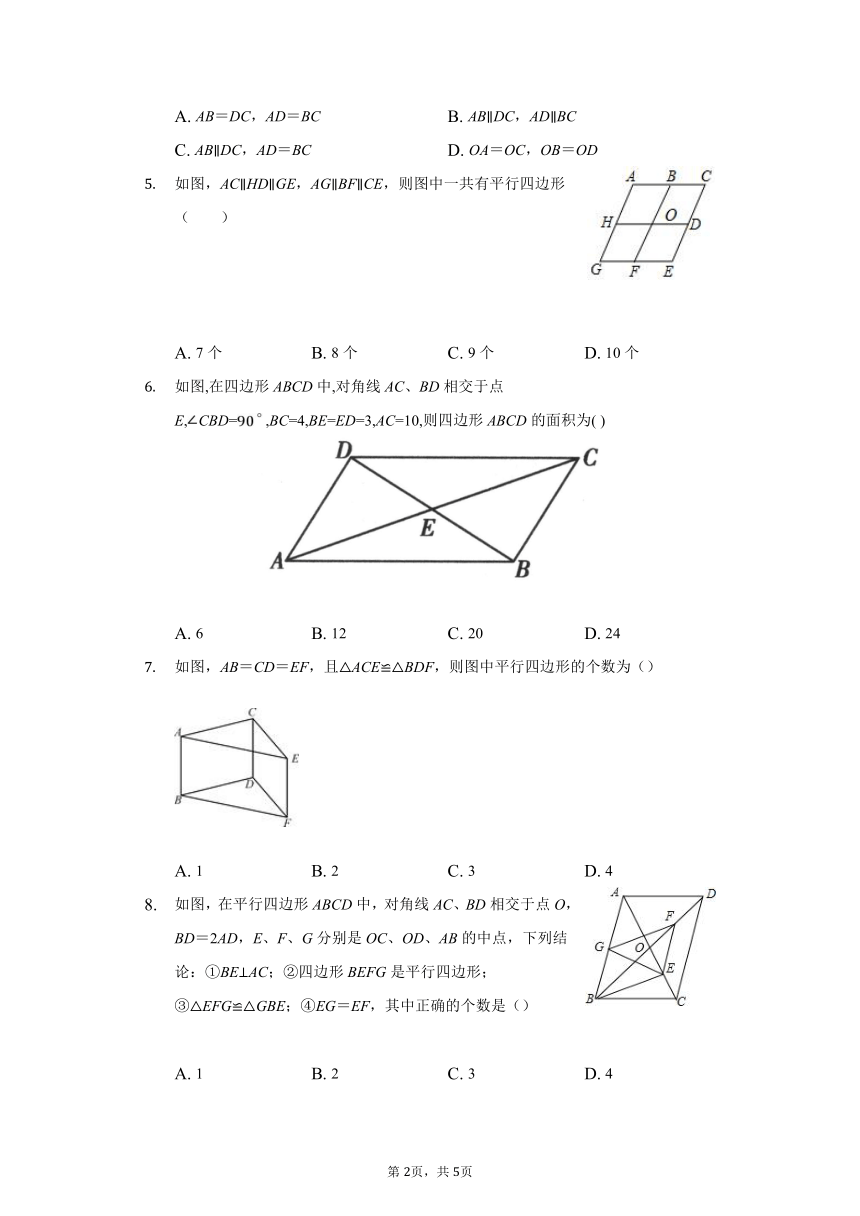
如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是()
A.
AB=DC,AD=BC
B.
AB∥DC,AD∥BC
C.
AB∥DC,AD=BC
D.
OA=OC,OB=OD
如图,AC∥HD∥GE,AG∥BF∥CE,则图中一共有平行四边形( )
A.
7个
B.
8个
C.
9个
D.
10个
如图,在四边形ABCD中,对角线AC、BD相交于点E,CBD=,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(
)
A.
6
B.
12
C.
20
D.
24
如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为()?
???????
A.
1
B.
2
C.
3
D.
4
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②四边形BEFG是平行四边形;③△EFG≌△GBE;④EG=EF,其中正确的个数是()
A.
1
B.
2
C.
3
D.
4
如图所示,在□ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形(???
)
A.
OE=OF
B.
DE=BF
C.
∠ADE=∠CBF
D.
∠ABE=∠CDF
如图,在平面直角坐标系中,线段在轴上,将线段向上平移2个单位.再向右平移1个单位,得到线段,连接,,在轴上存在点,使的面积为四边形面积的一半,则点的坐标为__.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=____s时,以A、C、E、F为顶点四边形是平行四边形.
如图,?ABCD的面积为72cm2,P为?ABCD内部的任意一点,则图中阴影部分的面积之和为______
.
如图,在△ABE中,∠BAE=90°,AB=AE,BE=12cm,过点A作AF∥BE且点F在点A的右侧.点D从点A出发沿射线AF方向以1cm/秒的速度运动,同时点P从点E出发沿射线EB方向以2cm/秒的速度运动,在线段PE上取点C,使得PC=2cm,设点D的运动时间为x秒.当x=______秒时,以A,B,C,D为顶点的四边形是平行四边形.
如图,在□ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S
□AEPH=______.
如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为______时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为______时,.(直接写出结果)
已知:等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB方向运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D。
(1)如图,若点P在线段AB上时,过点P作PE⊥AC于E,线段DE的长是否改变?证明你的结论.
(2)若点P在AB的延长线上,以上结论还成立吗?试画出图形,并证明你的结论。
17.如图1,图2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图1所示的位置时,求证:CD=AE.
(2)把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图2),分别连接DF、EF.
①找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
②试判断四边形CDFE的形状,并说明理由.
第2页,共2页
第1页,共1页
平行四边形的判断
同步练习
下列说法正确的是( )
A.
对角线相等的四边形是平行四边形
B.
一组对边平行,另一组对边相等的四边形是平行四边形
C.
一组对边相等,一组对角相等的四边形是平行四边形
D.
一组对边平行且相等的四边形是平行四边形
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,那么阴影部分的面积是平行四边形ABCD面积的(?
?
?
)
A.
B.
C.
D.
如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有(?
?)
?
A.
5对
B.
6对
C.
7对
D.
8对
如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是()
A.
AB=DC,AD=BC
B.
AB∥DC,AD∥BC
C.
AB∥DC,AD=BC
D.
OA=OC,OB=OD
如图,AC∥HD∥GE,AG∥BF∥CE,则图中一共有平行四边形( )
A.
7个
B.
8个
C.
9个
D.
10个
如图,在四边形ABCD中,对角线AC、BD相交于点E,CBD=,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为(
)
A.
6
B.
12
C.
20
D.
24
如图,AB=CD=EF,且△ACE≌△BDF,则图中平行四边形的个数为()?
???????
A.
1
B.
2
C.
3
D.
4
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②四边形BEFG是平行四边形;③△EFG≌△GBE;④EG=EF,其中正确的个数是()
A.
1
B.
2
C.
3
D.
4
如图所示,在□ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形(???
)
A.
OE=OF
B.
DE=BF
C.
∠ADE=∠CBF
D.
∠ABE=∠CDF
如图,在平面直角坐标系中,线段在轴上,将线段向上平移2个单位.再向右平移1个单位,得到线段,连接,,在轴上存在点,使的面积为四边形面积的一半,则点的坐标为__.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=____s时,以A、C、E、F为顶点四边形是平行四边形.
如图,?ABCD的面积为72cm2,P为?ABCD内部的任意一点,则图中阴影部分的面积之和为______
.
如图,在△ABE中,∠BAE=90°,AB=AE,BE=12cm,过点A作AF∥BE且点F在点A的右侧.点D从点A出发沿射线AF方向以1cm/秒的速度运动,同时点P从点E出发沿射线EB方向以2cm/秒的速度运动,在线段PE上取点C,使得PC=2cm,设点D的运动时间为x秒.当x=______秒时,以A,B,C,D为顶点的四边形是平行四边形.
如图,在□ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则S
□AEPH=______.
如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为______时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为______时,.(直接写出结果)
已知:等边三角形ABC的边长为2,点P和Q分别从A和C两点同时出发,做匀速运动,且它们的速度相同.点P沿射线AB方向运动,点Q沿边BC的延长线运动,设PQ与直线AC相交于点D。
(1)如图,若点P在线段AB上时,过点P作PE⊥AC于E,线段DE的长是否改变?证明你的结论.
(2)若点P在AB的延长线上,以上结论还成立吗?试画出图形,并证明你的结论。
17.如图1,图2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图1所示的位置时,求证:CD=AE.
(2)把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图2),分别连接DF、EF.
①找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
②试判断四边形CDFE的形状,并说明理由.
第2页,共2页
第1页,共1页
