2020-2021学年苏科版八年级数学上册 第5章 平面直角坐标系复习课练习(word版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学上册 第5章 平面直角坐标系复习课练习(word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 593.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 20:23:50 | ||
图片预览


文档简介
第5章
平面直角坐标系复习课
一、选择题(共8小题;共40分)
1.
如图,,,
这三个点中,在第二象限内的点是
A.
,,
B.
,
C.
,
D.
2.
平面直角坐标系内的点
与点
关于
A.
轴对称
B.
轴对称
C.
原点对称
D.
直线
对称
3.
在平面直角坐标系中,将点
向右平移
个单位长度,所得的点的坐标是
A.
B.
C.
D.
4.
小明从一个景点回宾馆,在一个岔路口迷了路,问了四个人得到下列四种回答,其中能确定宾馆位置的是
A.
离这儿还有
B.
沿南北路一直向南走
C.
沿南北路走
D.
沿南北路一直向南走
5.
点
关于
轴对称的点的坐标是
A.
B.
C.
D.
6.
如图,甲、乙两名同学用围棋子做游戏.现轮到黑棋下子,黑棋下子后白棋再下一子,使黑棋的
个棋子组成轴对称图形,白棋的
个棋子也组成轴对称图形.设棋子的位置用数对表示,如点
在
,则下列下子方法不正确的是
A.
黑
,白
B.
黑
,白
C.
黑
,白
D.
黑
,白
7.
在平面直角坐标系中,已知
,.若在坐标轴上取点
,使
为等腰三角形,则满足条件的点
的个数是
A.
B.
C.
D.
8.
在平面直角坐标系中,点
向右平移
个单位长度得到点
,点
绕原点逆时针旋转
得到点
,则点
的坐标是
A.
B.
C.
D.
二、填空题(共11小题;共44分)
9.
在平面直角坐标系中,正方形
的顶点
,,
的坐标分别为
,,,则顶点
的坐标为
?.
10.
点
先向左平移
个单位长度,再向上平移
个单位长度,得到点
的坐标是
?.
11.
已知点
,则点
关于
轴的对称点的坐标是
?,点
关于原点
的对称点的坐标是
?.
12.
已知点
在第二象限,则
的取值范围是
?.
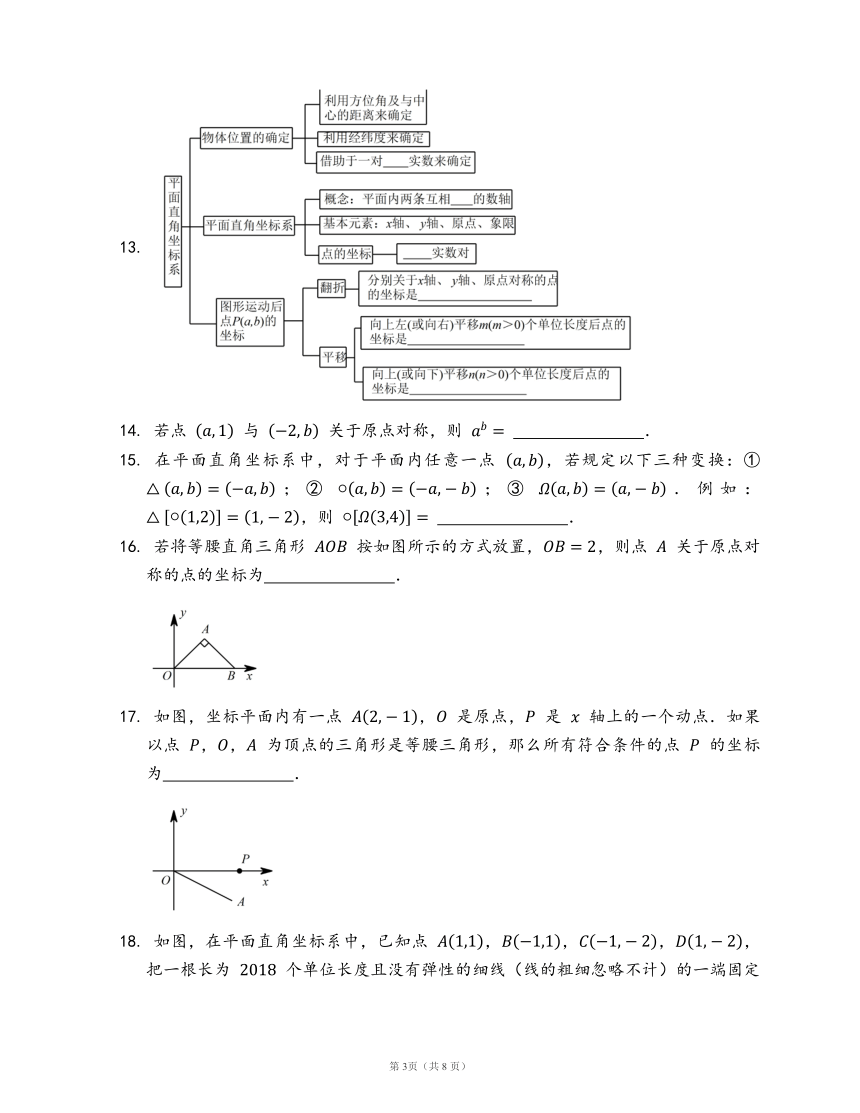
13.
14.
若点
与
关于原点对称,则
?.
15.
在平面直角坐标系中,对于平面内任意一点
,若规定以下三种变换:①
;②
;③
.例如:,则
?.
16.
若将等腰直角三角形
按如图所示的方式放置,,则点
关于原点对称的点的坐标为
?.
17.
如图,坐标平面内有一点
,
是原点,
是
轴上的一个动点.如果以点
,,
为顶点的三角形是等腰三角形,那么所有符合条件的点
的坐标为
?.
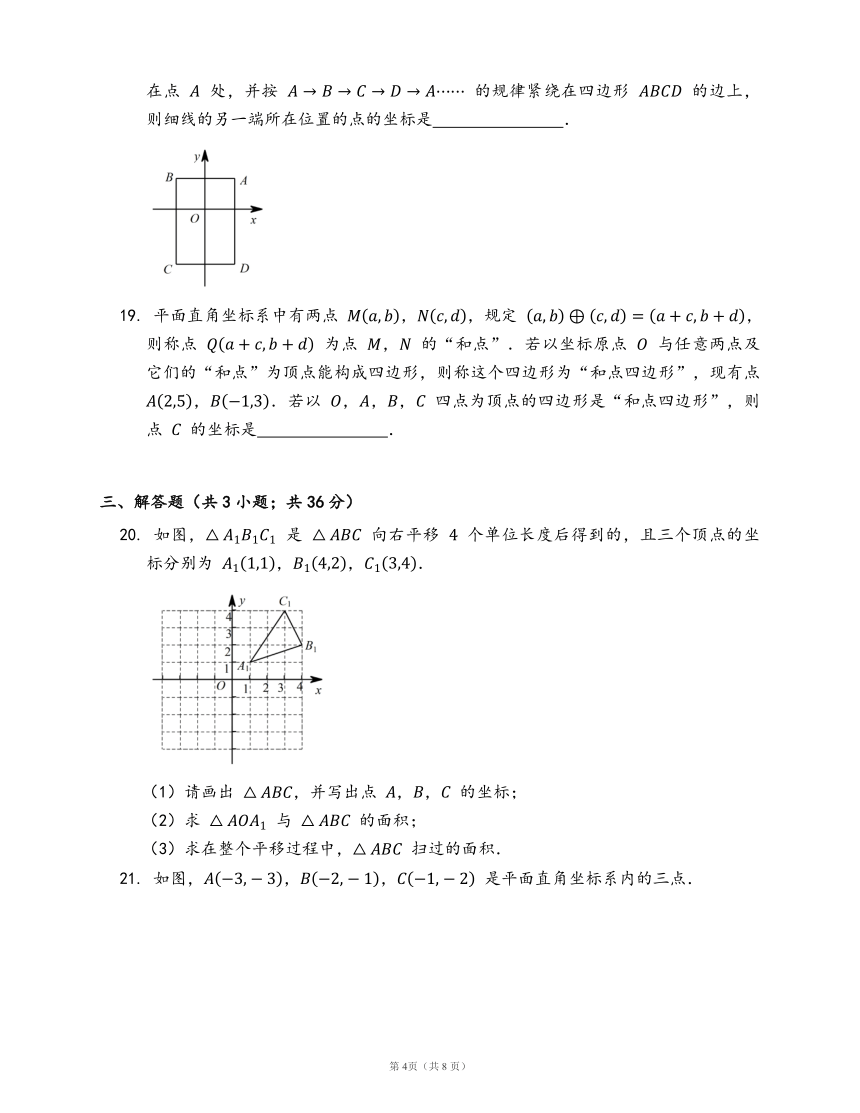
18.
如图,在平面直角坐标系中,已知点
,,,,把一根长为
个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点
处,并按
的规律紧绕在四边形
的边上,则细线的另一端所在位置的点的坐标是
?.
19.
平面直角坐标系中有两点
,,规定
,则称点
为点
,
的“和点”.若以坐标原点
与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点
,.若以
,,,
四点为顶点的四边形是“和点四边形”,则点
的坐标是
?.
三、解答题(共3小题;共36分)
20.
如图,
是
向右平移
个单位长度后得到的,且三个顶点的坐标分别为
,,.
(1)请画出
,并写出点
,,
的坐标;
(2)求
与
的面积;
(3)求在整个平移过程中,
扫过的面积.
21.
如图,,,
是平面直角坐标系内的三点.
(1)请画出
关于原点
对称的
;
(2)点
关于
轴对称的点
的坐标为
?,若将点
向上平移
个单位长度,使其落在
的内部,则
的取值范围为
?.
22.
如图,在平面直角坐标系
中,已知点
,,,,,,点
是四边形
内的一点,且
与
的面积相等,求
的值.
答案
第一部分
1.
D
2.
B
3.
D
4.
D
5.
D
6.
C
7.
A
8.
A
第二部分
9.
10.
11.
,
12.
13.
有序,垂直,有序,,,,
[或
],
[或
],
14.
15.
16.
17.
,,,
18.
19.
或
或
第三部分
20.
(1)
,,;
??????(2)
的面积为
,
的面积为
.
??????(3)
由平移的性质可知,四边形
是平行四边形,,
所以
扫过的面积为
.
21.
(1)
点拨:描出
,,
三点,再依次连接即可.
??????(2)
;
22.
如图,设
.
,,
,.
,,
,.
分别过点
,
作
,,分别交
,
的延长线于点
,.
,,
点
到
的距离为
,,,,,.
,
,
.
化简,得
,将左边分解因式,得
,
,
.
,即
.
.
第1页(共8
页)
平面直角坐标系复习课
一、选择题(共8小题;共40分)
1.
如图,,,
这三个点中,在第二象限内的点是
A.
,,
B.
,
C.
,
D.
2.
平面直角坐标系内的点
与点
关于
A.
轴对称
B.
轴对称
C.
原点对称
D.
直线
对称
3.
在平面直角坐标系中,将点
向右平移
个单位长度,所得的点的坐标是
A.
B.
C.
D.
4.
小明从一个景点回宾馆,在一个岔路口迷了路,问了四个人得到下列四种回答,其中能确定宾馆位置的是
A.
离这儿还有
B.
沿南北路一直向南走
C.
沿南北路走
D.
沿南北路一直向南走
5.
点
关于
轴对称的点的坐标是
A.
B.
C.
D.
6.
如图,甲、乙两名同学用围棋子做游戏.现轮到黑棋下子,黑棋下子后白棋再下一子,使黑棋的
个棋子组成轴对称图形,白棋的
个棋子也组成轴对称图形.设棋子的位置用数对表示,如点
在
,则下列下子方法不正确的是
A.
黑
,白
B.
黑
,白
C.
黑
,白
D.
黑
,白
7.
在平面直角坐标系中,已知
,.若在坐标轴上取点
,使
为等腰三角形,则满足条件的点
的个数是
A.
B.
C.
D.
8.
在平面直角坐标系中,点
向右平移
个单位长度得到点
,点
绕原点逆时针旋转
得到点
,则点
的坐标是
A.
B.
C.
D.
二、填空题(共11小题;共44分)
9.
在平面直角坐标系中,正方形
的顶点
,,
的坐标分别为
,,,则顶点
的坐标为
?.
10.
点
先向左平移
个单位长度,再向上平移
个单位长度,得到点
的坐标是
?.
11.
已知点
,则点
关于
轴的对称点的坐标是
?,点
关于原点
的对称点的坐标是
?.
12.
已知点
在第二象限,则
的取值范围是
?.
13.
14.
若点
与
关于原点对称,则
?.
15.
在平面直角坐标系中,对于平面内任意一点
,若规定以下三种变换:①
;②
;③
.例如:,则
?.
16.
若将等腰直角三角形
按如图所示的方式放置,,则点
关于原点对称的点的坐标为
?.
17.
如图,坐标平面内有一点
,
是原点,
是
轴上的一个动点.如果以点
,,
为顶点的三角形是等腰三角形,那么所有符合条件的点
的坐标为
?.
18.
如图,在平面直角坐标系中,已知点
,,,,把一根长为
个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点
处,并按
的规律紧绕在四边形
的边上,则细线的另一端所在位置的点的坐标是
?.
19.
平面直角坐标系中有两点
,,规定
,则称点
为点
,
的“和点”.若以坐标原点
与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点
,.若以
,,,
四点为顶点的四边形是“和点四边形”,则点
的坐标是
?.
三、解答题(共3小题;共36分)
20.
如图,
是
向右平移
个单位长度后得到的,且三个顶点的坐标分别为
,,.
(1)请画出
,并写出点
,,
的坐标;
(2)求
与
的面积;
(3)求在整个平移过程中,
扫过的面积.
21.
如图,,,
是平面直角坐标系内的三点.
(1)请画出
关于原点
对称的
;
(2)点
关于
轴对称的点
的坐标为
?,若将点
向上平移
个单位长度,使其落在
的内部,则
的取值范围为
?.
22.
如图,在平面直角坐标系
中,已知点
,,,,,,点
是四边形
内的一点,且
与
的面积相等,求
的值.
答案
第一部分
1.
D
2.
B
3.
D
4.
D
5.
D
6.
C
7.
A
8.
A
第二部分
9.
10.
11.
,
12.
13.
有序,垂直,有序,,,,
[或
],
[或
],
14.
15.
16.
17.
,,,
18.
19.
或
或
第三部分
20.
(1)
,,;
??????(2)
的面积为
,
的面积为
.
??????(3)
由平移的性质可知,四边形
是平行四边形,,
所以
扫过的面积为
.
21.
(1)
点拨:描出
,,
三点,再依次连接即可.
??????(2)
;
22.
如图,设
.
,,
,.
,,
,.
分别过点
,
作
,,分别交
,
的延长线于点
,.
,,
点
到
的距离为
,,,,,.
,
,
.
化简,得
,将左边分解因式,得
,
,
.
,即
.
.
第1页(共8
页)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
