宁夏海原县第一高中2020-2021学年高一上学期第二次月考(12月)数学试题 Word版含答案
文档属性
| 名称 | 宁夏海原县第一高中2020-2021学年高一上学期第二次月考(12月)数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 646.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 16:17:17 | ||
图片预览



文档简介
____________________________________________________________________________________________
海原一中2020-2021学年第一学期第二次月考
高一数学试卷
一、选择题(本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知全集
A. B. C. D.
2.下列叙述正确的是( )
A.方程的根构成的集合为
B.
C.集合表示的集合是
D.集合与集合是不同的集合
3.下列函数在其定义域内既是奇函数,又是减函数的是( )
A. B. C. D.
4.函数f(x)=的定义域是( )
A.(-3,0) B.(-3,0]
C.(-∞,-3)∪(0,+∞) D.(-∞,-3)∪(-3,0)
5.设是定义在上的函数,其图像关于原点对称,且当时,,
则( )
A.1 B.-1 C. D.
6.函数的零点所在的一个区间是( )
A. B. C. D.
7.设,,,则( )
A. B. C. D.
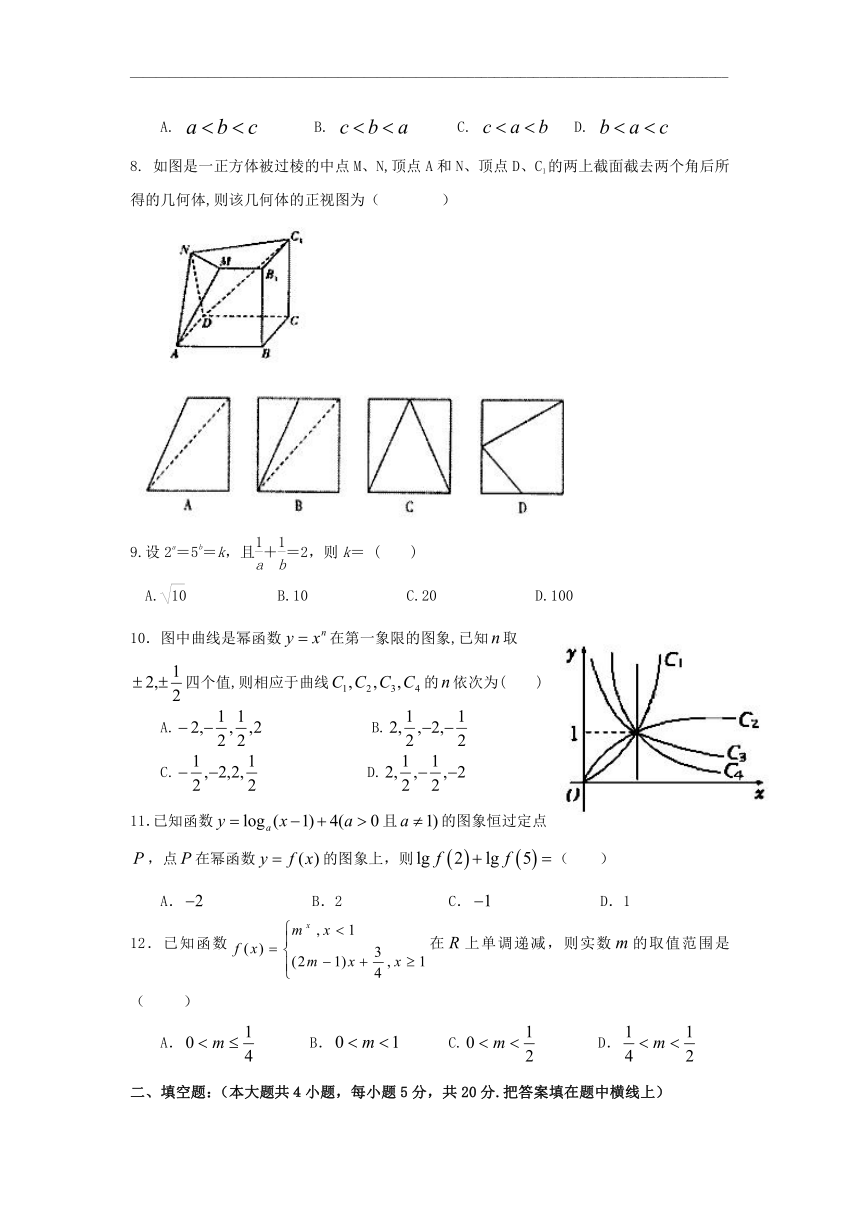
8. 如图是一正方体被过棱的中点M、N,顶点A和N、顶点D、C1的两上截面截去两个角后所得的几何体,则该几何体的正视图为( )
9.设2a=5b=k,且+=2,则k= ( )
A. B.10 C.20 D.100
10.图中曲线是幂函数在第一象限的图象,已知取四个值,则相应于曲线的依次为(??)
A. B.
C. D.[来源
11.已知函数且的图象恒过定点,点在幂函数的图象上,则( )
A. B.2 C. D.1
12.已知函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.已知集合,则它的真子集有______个。
14.已知函数是定义在上的偶函数,当时,是增函数,且,
则不等式的解集为___________。
15.函数的零点个数为 .
16.已知函数(其中、是常数),且,
则 .
三、解答题:共70分,解答应写出必要的文字说明、证明过程或演算步骤。
17.(本小题满分10分)已知集合,.
(1)分别求,;
(2)已知集合,若,求实数的取值集合
(本小题满分12分)
计算:(1);
(2)
19.(本小题满分12分)已知函数
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
20.(本小题满分12分)
已知函数,在上具有单调性,求实数k的取值范围.
(1)在上具有单调性,求实数k的取值范围;
(2)若恒成立,求k的取值范围.
21.(本小题满分12分)已知函数f(x)=loga(2-x)+loga(x+2),0<a<1.
(1)判断函数f(x)的奇偶性;
(2)若函数f(x)的最小值为-2,求a的值.
22.(本小题满分12分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元、0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系;
(2)若该家庭有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益是多少万元?
海原一中2020--2021学年第一学期高一年级第二次月考
数学参考答案
一、选择题:只有一项符合题目要求(共12小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B C A A B A B A D B A
二、填空题:(本大题共4小题,每小题5分,共20分)
13.3. 14. (-2,2) 15、2 16、5
三、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程和演算步骤,务必在答题纸指定的位置作答。)
17.
18.(1) 1 ------6分;
(2) 2/3 ------6分;
19.
20.
20.
21.(1)偶函数 ------6分
(2) ------6分
22.解:(1)设两类产品的收益与投资的函数分别为f(x)=k1x,g(x)=k2.
由已知得f(1)==k1,g(1)==k2,
所以f(x)=x(x≥0),g(x)=(x≥0).------5分
(2)设投资债券类产品为20-x万元,则投资股票类产品为x万元.
依题意得y=f(20-x)+g(x)=+=(0≤x≤20).
所以=2,即x=4时,收益最大,ymax=3万元.
故投资债券类产品16万元,投资股票类产品4万元时获得最大收益,为3万元---7分
海原一中2020-2021学年第一学期第二次月考
高一数学试卷
一、选择题(本大题共12小题,每小题5分,满分60分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知全集
A. B. C. D.
2.下列叙述正确的是( )
A.方程的根构成的集合为
B.
C.集合表示的集合是
D.集合与集合是不同的集合
3.下列函数在其定义域内既是奇函数,又是减函数的是( )
A. B. C. D.
4.函数f(x)=的定义域是( )
A.(-3,0) B.(-3,0]
C.(-∞,-3)∪(0,+∞) D.(-∞,-3)∪(-3,0)
5.设是定义在上的函数,其图像关于原点对称,且当时,,
则( )
A.1 B.-1 C. D.
6.函数的零点所在的一个区间是( )
A. B. C. D.
7.设,,,则( )
A. B. C. D.
8. 如图是一正方体被过棱的中点M、N,顶点A和N、顶点D、C1的两上截面截去两个角后所得的几何体,则该几何体的正视图为( )
9.设2a=5b=k,且+=2,则k= ( )
A. B.10 C.20 D.100
10.图中曲线是幂函数在第一象限的图象,已知取四个值,则相应于曲线的依次为(??)
A. B.
C. D.[来源
11.已知函数且的图象恒过定点,点在幂函数的图象上,则( )
A. B.2 C. D.1
12.已知函数在上单调递减,则实数的取值范围是( )
A. B. C. D.
二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
13.已知集合,则它的真子集有______个。
14.已知函数是定义在上的偶函数,当时,是增函数,且,
则不等式的解集为___________。
15.函数的零点个数为 .
16.已知函数(其中、是常数),且,
则 .
三、解答题:共70分,解答应写出必要的文字说明、证明过程或演算步骤。
17.(本小题满分10分)已知集合,.
(1)分别求,;
(2)已知集合,若,求实数的取值集合
(本小题满分12分)
计算:(1);
(2)
19.(本小题满分12分)已知函数
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
20.(本小题满分12分)
已知函数,在上具有单调性,求实数k的取值范围.
(1)在上具有单调性,求实数k的取值范围;
(2)若恒成立,求k的取值范围.
21.(本小题满分12分)已知函数f(x)=loga(2-x)+loga(x+2),0<a<1.
(1)判断函数f(x)的奇偶性;
(2)若函数f(x)的最小值为-2,求a的值.
22.(本小题满分12分)某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元、0.5万元.
(1)分别写出两类产品的收益与投资额的函数关系;
(2)若该家庭有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大收益,其最大收益是多少万元?
海原一中2020--2021学年第一学期高一年级第二次月考
数学参考答案
一、选择题:只有一项符合题目要求(共12小题,每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B B C A A B A B A D B A
二、填空题:(本大题共4小题,每小题5分,共20分)
13.3. 14. (-2,2) 15、2 16、5
三、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程和演算步骤,务必在答题纸指定的位置作答。)
17.
18.(1) 1 ------6分;
(2) 2/3 ------6分;
19.
20.
20.
21.(1)偶函数 ------6分
(2) ------6分
22.解:(1)设两类产品的收益与投资的函数分别为f(x)=k1x,g(x)=k2.
由已知得f(1)==k1,g(1)==k2,
所以f(x)=x(x≥0),g(x)=(x≥0).------5分
(2)设投资债券类产品为20-x万元,则投资股票类产品为x万元.
依题意得y=f(20-x)+g(x)=+=(0≤x≤20).
所以=2,即x=4时,收益最大,ymax=3万元.
故投资债券类产品16万元,投资股票类产品4万元时获得最大收益,为3万元---7分
同课章节目录
