2020-2021学年人教版九年级数学上册 24.4《弧长和扇形的面积公式》同步练习(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学上册 24.4《弧长和扇形的面积公式》同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 87.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览


文档简介
《弧长和扇形的面积公式》同步练习
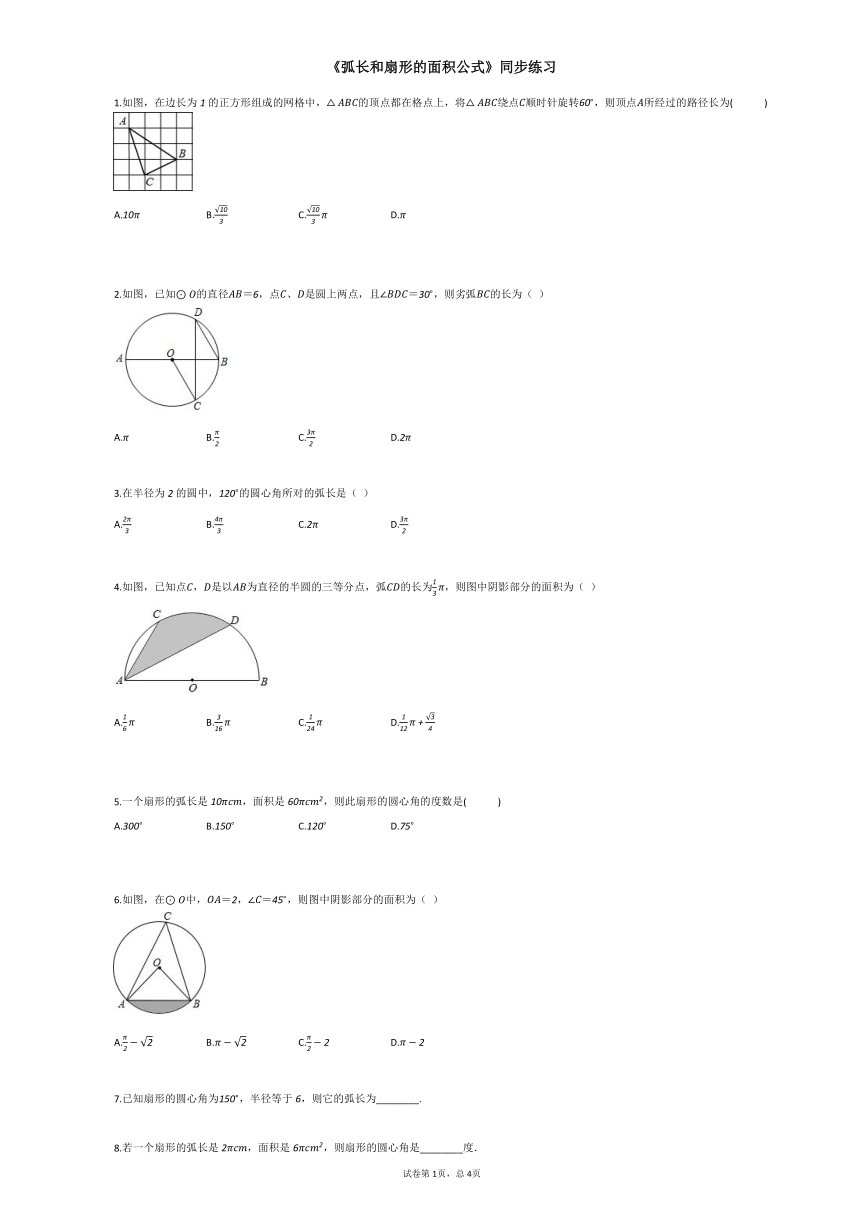
1.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60?,则顶点A所经过的路径长为(? ? ? ? )
A.10π B.103 C.103π D.π
?
2.如图,已知⊙O的直径AB=6,点C、D是圆上两点,且∠BDC=30?,则劣弧BC的长为( )
A.π B.π2 C.3π2 D.2π
3.在半径为2的圆中,120?的圆心角所对的弧长是( )
A.2π3 B.4π3 C.2π D.3π2
4.如图,已知点C,D是以AB为直径的半圆的三等分点,弧CD的长为13π,则图中阴影部分的面积为( )
A.16π B.316π C.124π D.112π+34
?
5.一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是(? ? ? ? )
A.300? B.150? C.120? D.75?
?
6.如图,在⊙O中,OA=2,∠C=45?,则图中阴影部分的面积为( )
A.π2?2 B.π?2 C.π2?2 D.π?2
?
7.已知扇形的圆心角为150?,半径等于6,则它的弧长为________.
?
8.若一个扇形的弧长是2πcm,面积是6πcm2,则扇形的圆心角是________度.
?
9.如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求EC的长度.
?
10.如图,在等腰△ABC中,AB=BC,∠A=30?,O为线段AC上一点,以O为圆心,线段OC的长为半径画圆恰好经过点B,与AC的另一个交点为D.
(1)求证:AB是⊙O的切线;
(2) 若⊙O的半径为1,求图中阴影部分的面积.
?
11.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小;
(2)求阴影部分的面积.
参考答案
1.【答案】C
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】5π
8.【答案】60
9.【答案】
证明:∵ BC?是⊙O?的直径,
∴ ∠BAC=90?,
∴ ∠ABE+∠AGB=90?;
∵ AD⊥BC,
∴ ∠C+∠CAD=90?;
∵ AB=AE,
∴ ∠C=∠ABE,
∴ ∠AGB=∠CAD,
∵ ∠C=∠BAD
∴ ∠BAD=∠ABE
∴ FA=FB.
如图,连接AO、EO,
,
∵ BD=DO=2,AD⊥BC,
∴ AB=AO,
∵ AO=BO,
∴ AB=AO=BO,
∴ △ABO是等边三角形,
∴ ∠AOB=60?,
∵ AB=AE,
∴ ∠AOE=60?,
∴ ∠EOC=60?,
∴ EC的长度=60×π×4180=43π.
10.【答案】
(1)证明:连接OB,
∵ AB=BC,
∴ ∠C=∠A=30?,∠CBA=120?,
∵ OC=OB,
∴ ∠OBC=∠C=30?,
∴ ∠OBA=90?,
∵ OB是⊙O的半径,
∴ AB是⊙O的切线.
(2)解:∵ ∠A=30?,OB=1,
∴ OA=2,由勾股定理得AB=3,
∴ S△ABO=12×1×3=32,
∵ S扇形OBD=60π×1360=π6,
∴ S阴影=S△ABO?S扇形OBD=32?π6.
11.【答案】
解:(1)∵ CD是圆O的直径,CD⊥AB,
∴ AD=BD,
∴ ∠C=12∠AOD,
∵ ∠AOD=∠COE,
∴ ∠C=12∠COE,
∵ AO⊥BC,
∴ ∠C=30?.
(2)连接OB,
由(1)知,∠C=30?,
∴ ∠AOD=60?,
∴ ∠AOB=120?,
在Rt△AOF中,AO=1,∠AOF=60?,
即∠OAF=30?,
∴ OF=12,AF=12?(12)2=32,
∴ AB=3,
∴ S阴影=S扇形OADB?S△OAB
=120π×12360?12×12×3
=13π?34.
1.如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60?,则顶点A所经过的路径长为(? ? ? ? )
A.10π B.103 C.103π D.π
?
2.如图,已知⊙O的直径AB=6,点C、D是圆上两点,且∠BDC=30?,则劣弧BC的长为( )
A.π B.π2 C.3π2 D.2π
3.在半径为2的圆中,120?的圆心角所对的弧长是( )
A.2π3 B.4π3 C.2π D.3π2
4.如图,已知点C,D是以AB为直径的半圆的三等分点,弧CD的长为13π,则图中阴影部分的面积为( )
A.16π B.316π C.124π D.112π+34
?
5.一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是(? ? ? ? )
A.300? B.150? C.120? D.75?
?
6.如图,在⊙O中,OA=2,∠C=45?,则图中阴影部分的面积为( )
A.π2?2 B.π?2 C.π2?2 D.π?2
?
7.已知扇形的圆心角为150?,半径等于6,则它的弧长为________.
?
8.若一个扇形的弧长是2πcm,面积是6πcm2,则扇形的圆心角是________度.
?
9.如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE分别交AD、AC于点F、G.
(1)证明:FA=FB;
(2)若BD=DO=2,求EC的长度.
?
10.如图,在等腰△ABC中,AB=BC,∠A=30?,O为线段AC上一点,以O为圆心,线段OC的长为半径画圆恰好经过点B,与AC的另一个交点为D.
(1)求证:AB是⊙O的切线;
(2) 若⊙O的半径为1,求图中阴影部分的面积.
?
11.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.
(1)求∠C的大小;
(2)求阴影部分的面积.
参考答案
1.【答案】C
2.【答案】A
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】D
7.【答案】5π
8.【答案】60
9.【答案】
证明:∵ BC?是⊙O?的直径,
∴ ∠BAC=90?,
∴ ∠ABE+∠AGB=90?;
∵ AD⊥BC,
∴ ∠C+∠CAD=90?;
∵ AB=AE,
∴ ∠C=∠ABE,
∴ ∠AGB=∠CAD,
∵ ∠C=∠BAD
∴ ∠BAD=∠ABE
∴ FA=FB.
如图,连接AO、EO,
,
∵ BD=DO=2,AD⊥BC,
∴ AB=AO,
∵ AO=BO,
∴ AB=AO=BO,
∴ △ABO是等边三角形,
∴ ∠AOB=60?,
∵ AB=AE,
∴ ∠AOE=60?,
∴ ∠EOC=60?,
∴ EC的长度=60×π×4180=43π.
10.【答案】
(1)证明:连接OB,
∵ AB=BC,
∴ ∠C=∠A=30?,∠CBA=120?,
∵ OC=OB,
∴ ∠OBC=∠C=30?,
∴ ∠OBA=90?,
∵ OB是⊙O的半径,
∴ AB是⊙O的切线.
(2)解:∵ ∠A=30?,OB=1,
∴ OA=2,由勾股定理得AB=3,
∴ S△ABO=12×1×3=32,
∵ S扇形OBD=60π×1360=π6,
∴ S阴影=S△ABO?S扇形OBD=32?π6.
11.【答案】
解:(1)∵ CD是圆O的直径,CD⊥AB,
∴ AD=BD,
∴ ∠C=12∠AOD,
∵ ∠AOD=∠COE,
∴ ∠C=12∠COE,
∵ AO⊥BC,
∴ ∠C=30?.
(2)连接OB,
由(1)知,∠C=30?,
∴ ∠AOD=60?,
∴ ∠AOB=120?,
在Rt△AOF中,AO=1,∠AOF=60?,
即∠OAF=30?,
∴ OF=12,AF=12?(12)2=32,
∴ AB=3,
∴ S阴影=S扇形OADB?S△OAB
=120π×12360?12×12×3
=13π?34.
同课章节目录
