人教高中数学必修一2.2.2对数函数及其性质 课件(27张ppt)
文档属性
| 名称 | 人教高中数学必修一2.2.2对数函数及其性质 课件(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
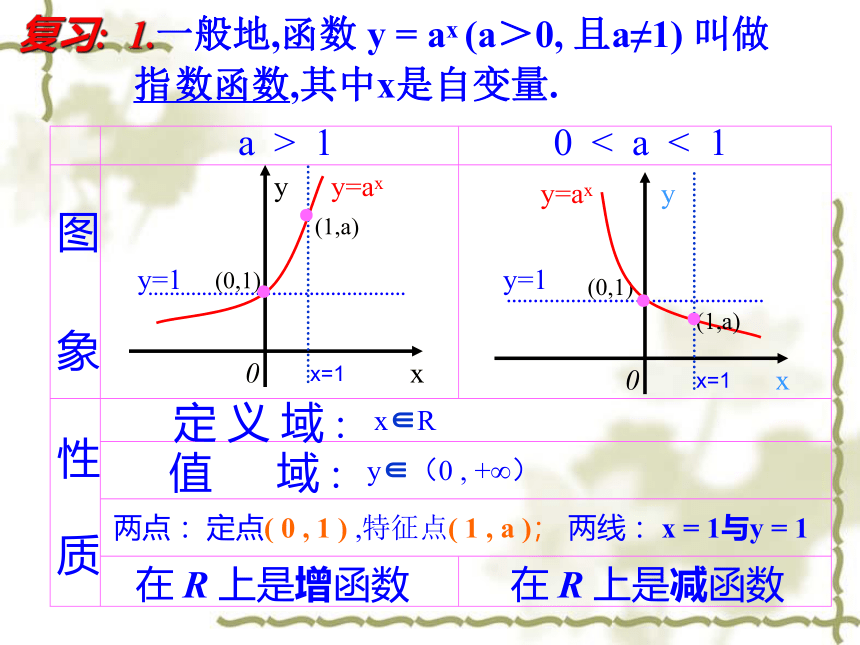
复习:
1.一般地,函数
y
=
ax
(a>0,
且a≠1)
叫做
指
数函数,其中x是自变量.
a
>
1
0
<
a
<
1
图
象
性
质
定
义
域
:
值
域
:
两点
:定点(
0
,
1
)
,特征点(
1
,
a
);
两线
:x
=
1与y
=
1
在
R
上是增函数
在
R
上是减函数
x∈R
y∈(0
,
+∞)
y=1
y
x
0
(0,1)
y=ax
x=1
●
(1,a)
●
y
x
(0,1)
y=1
0
y=ax
x=1
(1,a)
●
●
2、指数和对数的互化:
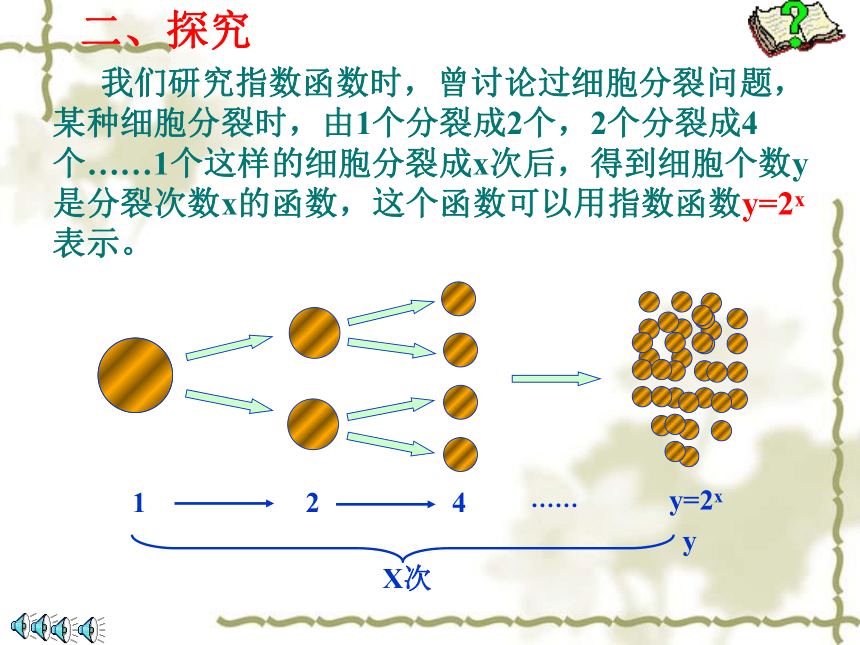
我们研究指数函数时,曾讨论过细胞分裂问题,某种细胞分裂时,由1个分裂成2个,2个分裂成4个……1个这样的细胞分裂成x次后,得到细胞个数y是分裂次数x的函数,这个函数可以用指数函数y=2x
表示。
1
2
4
y=2x
……
y
X次
二、探究
通常,我们习惯将x作为自变量,y作为函数值,所以写为对数函数:
当已知指数函数值求指数时,可将指数函数改写为与之等价的对数函数进行求值。
y=log2x
判断下列函数哪些是对数函数
在同一坐标系中用描点法画出对数函数
的图象。
作图步骤:
①列表
②描点
③连线
对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
探究:
X
1/4
1/2
1
2
4
…
y=log2x
-2
-1
0
1
2
…
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2
1
0
-1
-2
-2
-1
0
1
2
对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
…
…
…
…
…
…
图象特征
代数表述
定义域
:
(
0,+∞)
值
域
:
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
探究:对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
图象特征
函数性质
定义域
:
(
0,+∞)
值
域
:
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
探究:对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
探索发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
一般地,对数函数y=logax在a>1及0?
a>1
0<a<1
图
象
性
质
⑴定义域:
⑵值域:
⑶两点:
⑷单调性
:
⑷单调性:
(0,+∞)
R
定点(1,0),特征点(a,1);两线:x=1
与
y=1
在(0,+∞)上是增函数
在(0,+∞)上是减函数
当0<x<1时,y<0
当x>1时,y>0
当0<x<1时,y>0
当x>1时,y<0
(a,
1)
(a,
1)
o
y=ax
y=x
依据 对数函数y=
㏒ax和指数函数y=ax的图象关于直线y=x对称.
o
y=
㏒
x
y=
x
y=x
依据 对数函数y=
㏒ x和指数函数 的图象关于直线y=x对称.
y=
x
五、应用举例:
例1:求下列函数的定义域:
①y=logax2
②y=loga(4-x)
③y=loga(9-x2)
①因为x2
>0,即x≠0,
所以函数y=logax2
的定义域是{x│x≠0}
②因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x│x<4}
③因为9-x2>0,即-3所以函数y=loga(9-x2)的定义域是{x│-3解:
例2
比较下列各组数中两个值的大小:
⑴
log
23.4
,
log
28.5
⑵
log
0.31.8
,
log
0.32.7
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
解:
⑴考察对数函数
y
=
log
2x,因为
它的底数2>1,所以它在(0,+∞)
上
是增函数,于是log
23.4<log
28.5
⑵考察对数函数
y
=
log
0.3
x,因为它
的底数为0.3,即0<0.3<1,所以它
在(0,+∞)上是减函数,于是
log
0.31.8>log
0.32.7
log23.4
log28.5
y
0
3.4
8.5
x
y=log2x
0
log0.32.7
log0.31.8
y
1.8
2.7
x
y=log0.3x
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
y
0
5.1
5.9
x
loga5.9
loga5.1
y=logax
(a>1)
0
5.1
5.9
x
loga5.9
loga5.1
y
y=logax
(0对数函数的增减性决定于对数的底数是大于1还是小于1.
而已知条件
中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
当a>1时,函数y=log
ax在(0,+∞)上是增函数,于是
log
a5.1<log
a5.9
当0<a<1时,函数y=log
ax在(0,+∞)上是减函数,于是
log
a5.1>log
a5.9
<
<
>
>
练习:
比较下列各题中两个值的大小:
⑴
log106
log108
⑵
log0.56
log0.54
⑶
log0.10.5
log0.10.6
⑷
log1.51.6
log1.51.4
(5)log0.50.3__log20.8
>
2.当底数不确定时,要对底数a与1的大小进行分类讨论.
钥匙
1.当底数相同时,利用对数函数的单调性比较大小.
例3:比较下列各组数中两个值的大小:
log
2
7
与
log
5
7
解:∵
log
7
5
>
log
7
2
>0
∴
log
2
7
>
log
5
7
x
o
y
1
7
log
5
7
log
2
7
例4:比较下列各组数中两个值的大小:
log
7
6
log
7
7
log
6
7
log
7
6
log
3
2
log
2
0.8
钥匙
当底数不相同,真数也不相同时,利用“介值法”
常需引入中间值0或1(各种变形式).
log
6
7
log
6
6
log
3
2
log
3
1
log
2
0.8
log
2
1
>
<
>
<
=
1
=
1
>
=
0
=
0
>
log
6
7
log
7
6
log
3
2
log
2
0.8
>
>
(一)同底数比较大小
1.当底数确定时,则可由函数的
单调性直接进行判断;
2.当底数不确定时,应对底数进
行分类讨论。
(三)若底数、真数都不相同,
则常借
助1、0等中间量进行比较。
小结:两个对数比较大小
(二)同真数比较大小
1.通过换底公式;
2.利用函数图象。
C
log
,
log
,
log
,
log
则下列式子中正确的是(
)
的图像如图所示,
函数
x
y
x
y
x
y
x
y
d
c
b
a
=
=
=
=
1、
2、
3、
4、
例2:比较大小
对于y=ax,可以改写为函数x=logay,即,把y作为自变量,x作为函数值,这时我们就说x=logay是函数y=ax的反函数,并且
y=ax与x=logay互为反函数。由于我们常把x作为自变量,y作为函数值,所以把x=logay写成y=logax,即y=ax与y=logax互为反函数。
应注意,必须是两个函数才可以互为反函数,即定义域内的任意一个自变量x有且仅有1个与之对应的函数值y。
反函数的性质:一个函数的定义域就是它反函数的值域,值域就是它反函数的定义域。
1
、对数函数的概念
2
、对数函数的图像和性质
3
、会求定义域
4
、会用单调性比较大小
复习:
1.一般地,函数
y
=
ax
(a>0,
且a≠1)
叫做
指
数函数,其中x是自变量.
a
>
1
0
<
a
<
1
图
象
性
质
定
义
域
:
值
域
:
两点
:定点(
0
,
1
)
,特征点(
1
,
a
);
两线
:x
=
1与y
=
1
在
R
上是增函数
在
R
上是减函数
x∈R
y∈(0
,
+∞)
y=1
y
x
0
(0,1)
y=ax
x=1
●
(1,a)
●
y
x
(0,1)
y=1
0
y=ax
x=1
(1,a)
●
●
2、指数和对数的互化:
我们研究指数函数时,曾讨论过细胞分裂问题,某种细胞分裂时,由1个分裂成2个,2个分裂成4个……1个这样的细胞分裂成x次后,得到细胞个数y是分裂次数x的函数,这个函数可以用指数函数y=2x
表示。
1
2
4
y=2x
……
y
X次
二、探究
通常,我们习惯将x作为自变量,y作为函数值,所以写为对数函数:
当已知指数函数值求指数时,可将指数函数改写为与之等价的对数函数进行求值。
y=log2x
判断下列函数哪些是对数函数
在同一坐标系中用描点法画出对数函数
的图象。
作图步骤:
①列表
②描点
③连线
对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
探究:
X
1/4
1/2
1
2
4
…
y=log2x
-2
-1
0
1
2
…
列表
描点
作y=log2x图象
连线
2
1
-1
-2
1
2
4
0
y
x
3
对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
列表
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
x
1/4
1/2
1
2
4
2
1
0
-1
-2
-2
-1
0
1
2
对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
…
…
…
…
…
…
图象特征
代数表述
定义域
:
(
0,+∞)
值
域
:
R
增函数
在(0,+∞)上是:
探索发现:认真观察函数y=log2x
的图象填写下表
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐上升
探究:对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
2
1
-1
-2
1
2
4
0
y
x
3
图象特征
函数性质
定义域
:
(
0,+∞)
值
域
:
R
减函数
在(0,+∞)上是:
图象位于y轴右方
图象向上、向下无限延伸
自左向右看图象逐渐下降
探究:对数函数:y
=
loga
x
(a>0,且a≠
1)
图象与性质
探索发现:认真观察函数
的图象填写下表
2
1
-1
-2
1
2
4
0
y
x
3
一般地,对数函数y=logax在a>1及0
a>1
0<a<1
图
象
性
质
⑴定义域:
⑵值域:
⑶两点:
⑷单调性
:
⑷单调性:
(0,+∞)
R
定点(1,0),特征点(a,1);两线:x=1
与
y=1
在(0,+∞)上是增函数
在(0,+∞)上是减函数
当0<x<1时,y<0
当x>1时,y>0
当0<x<1时,y>0
当x>1时,y<0
(a,
1)
(a,
1)
o
y=ax
y=x
依据 对数函数y=
㏒ax和指数函数y=ax的图象关于直线y=x对称.
o
y=
㏒
x
y=
x
y=x
依据 对数函数y=
㏒ x和指数函数 的图象关于直线y=x对称.
y=
x
五、应用举例:
例1:求下列函数的定义域:
①y=logax2
②y=loga(4-x)
③y=loga(9-x2)
①因为x2
>0,即x≠0,
所以函数y=logax2
的定义域是{x│x≠0}
②因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x│x<4}
③因为9-x2>0,即-3
例2
比较下列各组数中两个值的大小:
⑴
log
23.4
,
log
28.5
⑵
log
0.31.8
,
log
0.32.7
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
解:
⑴考察对数函数
y
=
log
2x,因为
它的底数2>1,所以它在(0,+∞)
上
是增函数,于是log
23.4<log
28.5
⑵考察对数函数
y
=
log
0.3
x,因为它
的底数为0.3,即0<0.3<1,所以它
在(0,+∞)上是减函数,于是
log
0.31.8>log
0.32.7
log23.4
log28.5
y
0
3.4
8.5
x
y=log2x
0
log0.32.7
log0.31.8
y
1.8
2.7
x
y=log0.3x
⑶
log
a5.1
,
log
a5.9
(
a>0
,
a≠1
)
y
0
5.1
5.9
x
loga5.9
loga5.1
y=logax
(a>1)
0
5.1
5.9
x
loga5.9
loga5.1
y
y=logax
(0
而已知条件
中并未指出底数a与1哪个大,因此需要对底数a进行讨论:
当a>1时,函数y=log
ax在(0,+∞)上是增函数,于是
log
a5.1<log
a5.9
当0<a<1时,函数y=log
ax在(0,+∞)上是减函数,于是
log
a5.1>log
a5.9
<
<
>
>
练习:
比较下列各题中两个值的大小:
⑴
log106
log108
⑵
log0.56
log0.54
⑶
log0.10.5
log0.10.6
⑷
log1.51.6
log1.51.4
(5)log0.50.3__log20.8
>
2.当底数不确定时,要对底数a与1的大小进行分类讨论.
钥匙
1.当底数相同时,利用对数函数的单调性比较大小.
例3:比较下列各组数中两个值的大小:
log
2
7
与
log
5
7
解:∵
log
7
5
>
log
7
2
>0
∴
log
2
7
>
log
5
7
x
o
y
1
7
log
5
7
log
2
7
例4:比较下列各组数中两个值的大小:
log
7
6
log
7
7
log
6
7
log
7
6
log
3
2
log
2
0.8
钥匙
当底数不相同,真数也不相同时,利用“介值法”
常需引入中间值0或1(各种变形式).
log
6
7
log
6
6
log
3
2
log
3
1
log
2
0.8
log
2
1
>
<
>
<
=
1
=
1
>
=
0
=
0
>
log
6
7
log
7
6
log
3
2
log
2
0.8
>
>
(一)同底数比较大小
1.当底数确定时,则可由函数的
单调性直接进行判断;
2.当底数不确定时,应对底数进
行分类讨论。
(三)若底数、真数都不相同,
则常借
助1、0等中间量进行比较。
小结:两个对数比较大小
(二)同真数比较大小
1.通过换底公式;
2.利用函数图象。
C
log
,
log
,
log
,
log
则下列式子中正确的是(
)
的图像如图所示,
函数
x
y
x
y
x
y
x
y
d
c
b
a
=
=
=
=
1、
2、
3、
4、
例2:比较大小
对于y=ax,可以改写为函数x=logay,即,把y作为自变量,x作为函数值,这时我们就说x=logay是函数y=ax的反函数,并且
y=ax与x=logay互为反函数。由于我们常把x作为自变量,y作为函数值,所以把x=logay写成y=logax,即y=ax与y=logax互为反函数。
应注意,必须是两个函数才可以互为反函数,即定义域内的任意一个自变量x有且仅有1个与之对应的函数值y。
反函数的性质:一个函数的定义域就是它反函数的值域,值域就是它反函数的定义域。
1
、对数函数的概念
2
、对数函数的图像和性质
3
、会求定义域
4
、会用单调性比较大小
