人教版数学七年级上册 第四章《图形认识初步》复习 教学设计
文档属性
| 名称 | 人教版数学七年级上册 第四章《图形认识初步》复习 教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 134.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览


文档简介
第四章《图形认识初步》复习
教学设计
内容和内容解析
1.内容
章末复习题4:几何图形的分类,线段和直线的基本事实及其应用;
2.内容解析
本章是图形与几何内容的开始,是学习后续相关知识的基础,研究问题的方法也是今后研究相关内容的重要方法,所以引导学生复习梳理所学内容很重要,在寻找知识点联系的过程中,逐步建立知识体系.
二.目标和目标解析
1.目标
(1)熟练地对几何图形进行分类;
(2)运用线段和直线的基本事实解决应用问题;
(3)利用余角的性质解决图形中的角的关系问题;
(4)了解"中点四边形"的概念.
2.目标解析
达成目标(1)的标志是:通过观察,迅速地对立体图形和几何图形进行转化;
达成目标(2)的标志是:能够准确地运用几何语言描述实际问题,体会这两个基本事实的应用价值;
达成目标(3)的标志是:学生在动手操作的过程中,把角之间的数量关系表示出来;
达成目标(4)的标志是:学生通过测量任意四边形的"中点四边形"的边长的内角,找到关于边长之间关系和内角之间关系的猜想.
教学问题诊断分析
几何是研究图形的形状、大小和位置关系的学科。本章我们学习了图形与几何的一些最基本的知识,如几何图形、立体图形、平面图形;了解了线段和直线的基本事实,并会运用几何语言描述基本事实的应用;本章学生初次接触几何与图形的基本概念,线段、角的概念比较抽象,这种抽象性是教学中的难点,通过复习,加深理解;另外,对图形的表示和画图以及几何运用的运用,都需要通过练习加以巩固。
教学问题诊断分析
在小学阶段,学生已经有了对于“直线、线段、射线”的感性认识,在本章中,学生进一步学习了“直线、线段、射线”的表示方法,经历了“几何模型
图形
文字
符号”,再由“符号语言
文字语言
图形语言”的转换过程,是比较困难的学习任务,在复习中帮助学生达到三种语言的自由转换。
本节课的复习难点:余角性质的应用;空间观念的建立和发展;几何语言的认识与运用。
教学过程设计
问题1、我们知道几何是研究图形的形状、大小和位置关系的学科,在第四章《几何图形初步》这一章中我们学习了图形与几何的一些最基本的知识,我们知道了几何图形分为立体图形和平面图形;知道了点动成线、线动成面、面动成体,我们还学会了将一个立方体展开成平面图形的各种方法,同学们还记得一共有几种情况吗?
师生活动:学生思考,口答;
设计意图:唤醒学生原有知识结构中的基本概念。
【教学方法】:小组合作探究法
【教学用具】:教材,投影仪,电子白板,希沃授课助手软件
【教学课时】:一课时
【教学过程】
复习巩固
问题2、探究并回答下列问题
立体图形与平面图形的相互转化(PPT展示)
1、对应练习:教材
P147-4
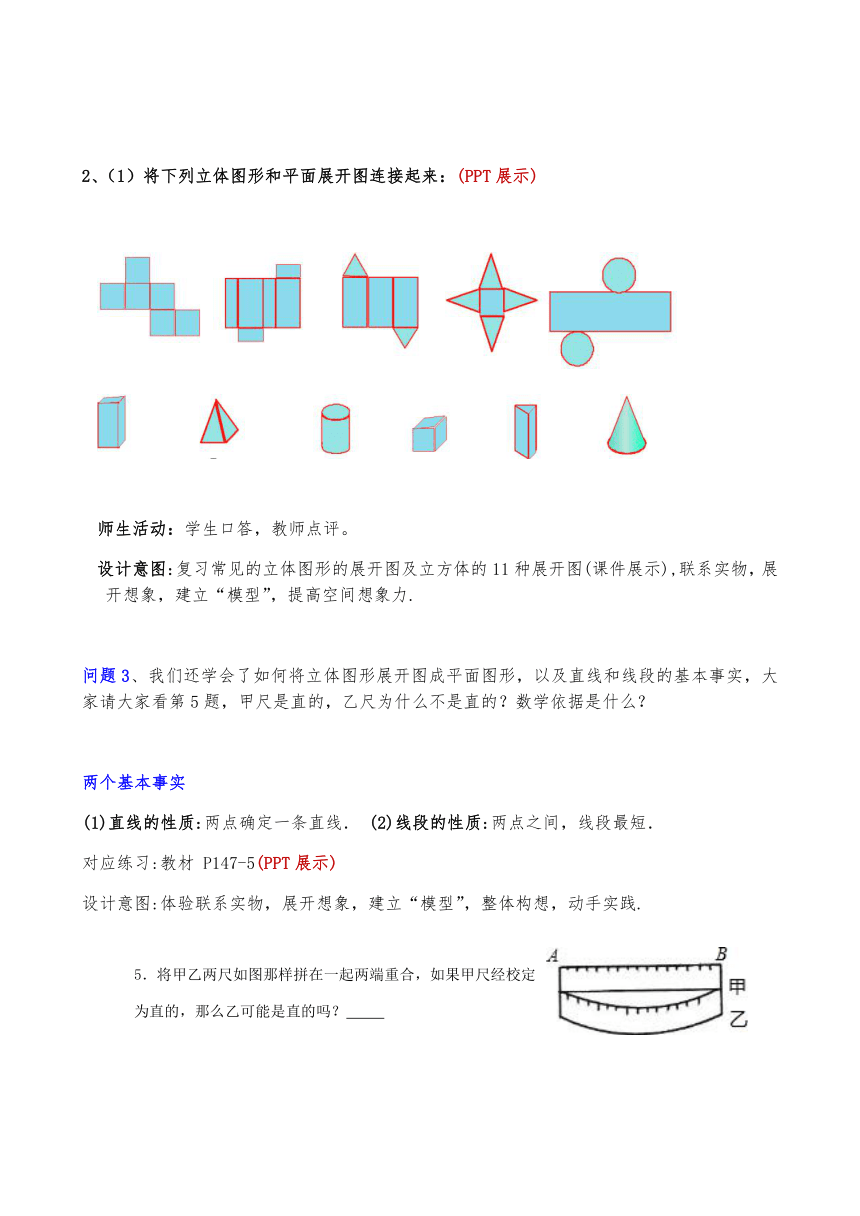
2、(1)将下列立体图形和平面展开图连接起来:(PPT展示)
师生活动:学生口答,教师点评。
设计意图:复习常见的立体图形的展开图及立方体的11种展开图(课件展示),联系实物,展开想象,建立“模型”,提高空间想象力.
问题3、我们还学会了如何将立体图形展开图成平面图形,以及直线和线段的基本事实,大家请大家看第5题,甲尺是直的,乙尺为什么不是直的?数学依据是什么?
两个基本事实
(1)直线的性质:两点确定一条直线.
(2)线段的性质:两点之间,线段最短.
对应练习:教材
P147-5(PPT展示)
设计意图:体验联系实物,展开想象,建立“模型”,整体构想,动手实践.
师生活动:学生独立思考,回答问题.
设计意图:加深对“两点确定一条直线”的理解,并体会这一事实的应用价值。
问题4、在这一章中,我们学习了线段的和差和角的平分线等知识点,,这些都是进一步学习图形与几何知识的基础。下面请大家完成第6题
对应练习:教材
P147-6
在如图所示的一张零件图中,已知AD=76mm,BD=70mm,CD=19mm,求AB和BC的长.
(PPT展示)学生讲解板演
【分析】根据线段的和差,可得答案.
【解答】解:由线段的和差,得
AB=AD﹣BD=73﹣69=4(mm),
BC=BD﹣CD=69﹣17=52(mm).
【点评】本题考查了两点间的距离,利用了线段的和差,即AB=AD﹣BD,BC=BD﹣CD.
师生活动:学生独立思考并完成书写,一名学生板书并讲解,教师点拨。
设计意图:
培养学生的识图能力,在图形和相应数量关系之间建立联系,对于以后的学习很有帮助。
问题5、我们继续,请大家独立思考第9题,限时30秒,然后小组交换意见,60秒,各组分享。
师生活动:自主学习,小组交流,汇报展示,教师点拨。
设计意图:这道题是应用展开图解决空间数学问题,关键词是“最短”,涉及到线段的基本事实“两点之间线段最短”。
对应练习:教材
P147-9(PPT展示)
如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
问题6、下面请大家思考第11题
11.如图,A、B两地隔着湖水,从C地测得CA=50m,CB=60m,
∠ACB=145°,用1厘米代表10米(就是1:1000的比例尺)
画出如图的图形.量出AB的长(精确到1毫米),再换算出AB间的实际距离.(PPT展示,希沃软件实时展示学生答案)
【分析】根据比例尺的定义,1厘米代表10米,把CA=50m,CB=60m,转化为CA=5cm,CB=6cm,结合题意画图,再测量AB的长,最后换算出A、B间的实际距离.
【解答】解:如图,测得AB长约10.5cm,换算成实际距离约为10.5×1000=10500cm=105m.
即A、B间的实际距离是105m.
【点评】本题考查了比例问题以及两点之间的距离是连接两点的线段的长度.
师生活动:学生独立思考并完成书写,一名学生讲解,教师将学生的分析过程用希沃软件投屏到大屏幕。
设计意图:通过画图解决不可解决的测量问题,将实际问题转化为数学问题,感受数学的应用价值。
四:.角的互余互补关系
12.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,
连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,
得折痕EN,求∠NEM的度数.并直接写出∠B′ME互余的角.
(PPT展示,希沃软件实时展示学生答案)
【分析】先由翻折的性质得到∠AEN=∠A′EN,∠BEM=∠B′EM,从而可知∠NEM=×180°=90°,然后根据余角的定义找出∠B′ME的余角即可.
【解答】解:由翻折的性质可知:∠AEN=∠A′EN,∠BEM=∠B′EM.
∠NEM=∠A′EN+∠B′EM==×180°=90°.
由翻折的性质可知:∠MB′E=∠B=90°.
由直角三角形两锐角互余可知:∠B′ME的一个余角是∠B′EM.
∵∠BEM=∠B′EM,
∴∠BEM也是∠B′ME的一个余角.
∵∠NBF+∠B′EM=90°,
∴∠NEF=∠B′ME.
∴∠ANE、∠A′NE是∠B′ME的余角.
综上所述,∠B′ME的余角有∠ANE、∠A′NE、∠B′EM、∠BEM.
师生活动:学生独立思考并完成书写,一名学生讲解,教师将学生的分析过程用希沃软件投屏到大屏幕。
设计意图:本题为一个动手操作的题,学生在本章的学习中已经掌握了翻折的特性,具有了一定的空间想象能力,可以把翻折过程中的角之间的关系表达清楚,体会一个角的余角不止一个,只和度数有关,和位置无关.
拓广探索
14.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH.(PPT展示)
师生活动:学生独立思考并猜想结论,教师几何画板展示动态图形。
设计意图:让学生通过测量从中寻找关于边长之间关系和内角之间关系的猜想,鼓励学生
大胆猜想,勇于探索.
教学设计
内容和内容解析
1.内容
章末复习题4:几何图形的分类,线段和直线的基本事实及其应用;
2.内容解析
本章是图形与几何内容的开始,是学习后续相关知识的基础,研究问题的方法也是今后研究相关内容的重要方法,所以引导学生复习梳理所学内容很重要,在寻找知识点联系的过程中,逐步建立知识体系.
二.目标和目标解析
1.目标
(1)熟练地对几何图形进行分类;
(2)运用线段和直线的基本事实解决应用问题;
(3)利用余角的性质解决图形中的角的关系问题;
(4)了解"中点四边形"的概念.
2.目标解析
达成目标(1)的标志是:通过观察,迅速地对立体图形和几何图形进行转化;
达成目标(2)的标志是:能够准确地运用几何语言描述实际问题,体会这两个基本事实的应用价值;
达成目标(3)的标志是:学生在动手操作的过程中,把角之间的数量关系表示出来;
达成目标(4)的标志是:学生通过测量任意四边形的"中点四边形"的边长的内角,找到关于边长之间关系和内角之间关系的猜想.
教学问题诊断分析
几何是研究图形的形状、大小和位置关系的学科。本章我们学习了图形与几何的一些最基本的知识,如几何图形、立体图形、平面图形;了解了线段和直线的基本事实,并会运用几何语言描述基本事实的应用;本章学生初次接触几何与图形的基本概念,线段、角的概念比较抽象,这种抽象性是教学中的难点,通过复习,加深理解;另外,对图形的表示和画图以及几何运用的运用,都需要通过练习加以巩固。
教学问题诊断分析
在小学阶段,学生已经有了对于“直线、线段、射线”的感性认识,在本章中,学生进一步学习了“直线、线段、射线”的表示方法,经历了“几何模型
图形
文字
符号”,再由“符号语言
文字语言
图形语言”的转换过程,是比较困难的学习任务,在复习中帮助学生达到三种语言的自由转换。
本节课的复习难点:余角性质的应用;空间观念的建立和发展;几何语言的认识与运用。
教学过程设计
问题1、我们知道几何是研究图形的形状、大小和位置关系的学科,在第四章《几何图形初步》这一章中我们学习了图形与几何的一些最基本的知识,我们知道了几何图形分为立体图形和平面图形;知道了点动成线、线动成面、面动成体,我们还学会了将一个立方体展开成平面图形的各种方法,同学们还记得一共有几种情况吗?
师生活动:学生思考,口答;
设计意图:唤醒学生原有知识结构中的基本概念。
【教学方法】:小组合作探究法
【教学用具】:教材,投影仪,电子白板,希沃授课助手软件
【教学课时】:一课时
【教学过程】
复习巩固
问题2、探究并回答下列问题
立体图形与平面图形的相互转化(PPT展示)
1、对应练习:教材
P147-4
2、(1)将下列立体图形和平面展开图连接起来:(PPT展示)
师生活动:学生口答,教师点评。
设计意图:复习常见的立体图形的展开图及立方体的11种展开图(课件展示),联系实物,展开想象,建立“模型”,提高空间想象力.
问题3、我们还学会了如何将立体图形展开图成平面图形,以及直线和线段的基本事实,大家请大家看第5题,甲尺是直的,乙尺为什么不是直的?数学依据是什么?
两个基本事实
(1)直线的性质:两点确定一条直线.
(2)线段的性质:两点之间,线段最短.
对应练习:教材
P147-5(PPT展示)
设计意图:体验联系实物,展开想象,建立“模型”,整体构想,动手实践.
师生活动:学生独立思考,回答问题.
设计意图:加深对“两点确定一条直线”的理解,并体会这一事实的应用价值。
问题4、在这一章中,我们学习了线段的和差和角的平分线等知识点,,这些都是进一步学习图形与几何知识的基础。下面请大家完成第6题
对应练习:教材
P147-6
在如图所示的一张零件图中,已知AD=76mm,BD=70mm,CD=19mm,求AB和BC的长.
(PPT展示)学生讲解板演
【分析】根据线段的和差,可得答案.
【解答】解:由线段的和差,得
AB=AD﹣BD=73﹣69=4(mm),
BC=BD﹣CD=69﹣17=52(mm).
【点评】本题考查了两点间的距离,利用了线段的和差,即AB=AD﹣BD,BC=BD﹣CD.
师生活动:学生独立思考并完成书写,一名学生板书并讲解,教师点拨。
设计意图:
培养学生的识图能力,在图形和相应数量关系之间建立联系,对于以后的学习很有帮助。
问题5、我们继续,请大家独立思考第9题,限时30秒,然后小组交换意见,60秒,各组分享。
师生活动:自主学习,小组交流,汇报展示,教师点拨。
设计意图:这道题是应用展开图解决空间数学问题,关键词是“最短”,涉及到线段的基本事实“两点之间线段最短”。
对应练习:教材
P147-9(PPT展示)
如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
问题6、下面请大家思考第11题
11.如图,A、B两地隔着湖水,从C地测得CA=50m,CB=60m,
∠ACB=145°,用1厘米代表10米(就是1:1000的比例尺)
画出如图的图形.量出AB的长(精确到1毫米),再换算出AB间的实际距离.(PPT展示,希沃软件实时展示学生答案)
【分析】根据比例尺的定义,1厘米代表10米,把CA=50m,CB=60m,转化为CA=5cm,CB=6cm,结合题意画图,再测量AB的长,最后换算出A、B间的实际距离.
【解答】解:如图,测得AB长约10.5cm,换算成实际距离约为10.5×1000=10500cm=105m.
即A、B间的实际距离是105m.
【点评】本题考查了比例问题以及两点之间的距离是连接两点的线段的长度.
师生活动:学生独立思考并完成书写,一名学生讲解,教师将学生的分析过程用希沃软件投屏到大屏幕。
设计意图:通过画图解决不可解决的测量问题,将实际问题转化为数学问题,感受数学的应用价值。
四:.角的互余互补关系
12.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,
连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,
得折痕EN,求∠NEM的度数.并直接写出∠B′ME互余的角.
(PPT展示,希沃软件实时展示学生答案)
【分析】先由翻折的性质得到∠AEN=∠A′EN,∠BEM=∠B′EM,从而可知∠NEM=×180°=90°,然后根据余角的定义找出∠B′ME的余角即可.
【解答】解:由翻折的性质可知:∠AEN=∠A′EN,∠BEM=∠B′EM.
∠NEM=∠A′EN+∠B′EM==×180°=90°.
由翻折的性质可知:∠MB′E=∠B=90°.
由直角三角形两锐角互余可知:∠B′ME的一个余角是∠B′EM.
∵∠BEM=∠B′EM,
∴∠BEM也是∠B′ME的一个余角.
∵∠NBF+∠B′EM=90°,
∴∠NEF=∠B′ME.
∴∠ANE、∠A′NE是∠B′ME的余角.
综上所述,∠B′ME的余角有∠ANE、∠A′NE、∠B′EM、∠BEM.
师生活动:学生独立思考并完成书写,一名学生讲解,教师将学生的分析过程用希沃软件投屏到大屏幕。
设计意图:本题为一个动手操作的题,学生在本章的学习中已经掌握了翻折的特性,具有了一定的空间想象能力,可以把翻折过程中的角之间的关系表达清楚,体会一个角的余角不止一个,只和度数有关,和位置无关.
拓广探索
14.已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH.(PPT展示)
师生活动:学生独立思考并猜想结论,教师几何画板展示动态图形。
设计意图:让学生通过测量从中寻找关于边长之间关系和内角之间关系的猜想,鼓励学生
大胆猜想,勇于探索.
