4.4单个一次函数图象的应用(第2课时) 课件(共27张PPT)
文档属性
| 名称 | 4.4单个一次函数图象的应用(第2课时) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 903.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 15:04:57 | ||
图片预览





文档简介
导入新课
1.由一次函数的图象可确定k 和 b 的符号;
2.由一次函数的图象可估计函数的变化趋势;
3.可直接观察出:x与y 的对应值;
4.由一次函数的图象与y 轴的交点的坐标可确定b值,
从而确定一次函数的图象的表达式.
从一次函数图象可获得哪些信息?
第2课时 单个一次函数图象的应用
4.4 一次函数的应用
学习目标
1.掌握单个一次函数图象的应用.(重点)
2.了解一次函数与一元一次方程的关系.
(难点)
新知导入
想一想:一次函数具有什么性质?
在一次函数y=kx+b中:
当k>0时,y随x的增大而增大,
当b>0时,直线交y轴于正半轴,必过一、二、三象限;
当b<0时,直线交y轴于负半轴,必过一、三、四象限.
当k<0时,y随x的增大而减小,
当b>0时,直线交y轴于正半轴,必过一、二、四象限;
当b<0时,直线交y轴于负半轴,必过二、三、四象限.
新知导入
在前几节课里,我们通过从生活中的实际问题情景出发,分别学习了一次函数,一次函数的图象,一次函数图象的性质,从中对一次函数在现实生活中的广泛应用有了一定的了解.
怎样应用一次函数的图象和性质来解决现实生活中的实际问题,是我们这节课的主要内容.
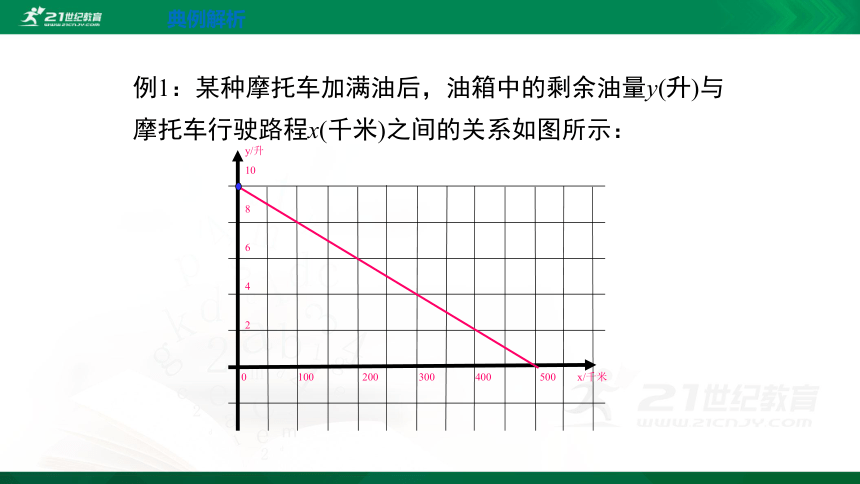
例1:某种摩托车加满油后,油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图所示:
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
典例解析
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
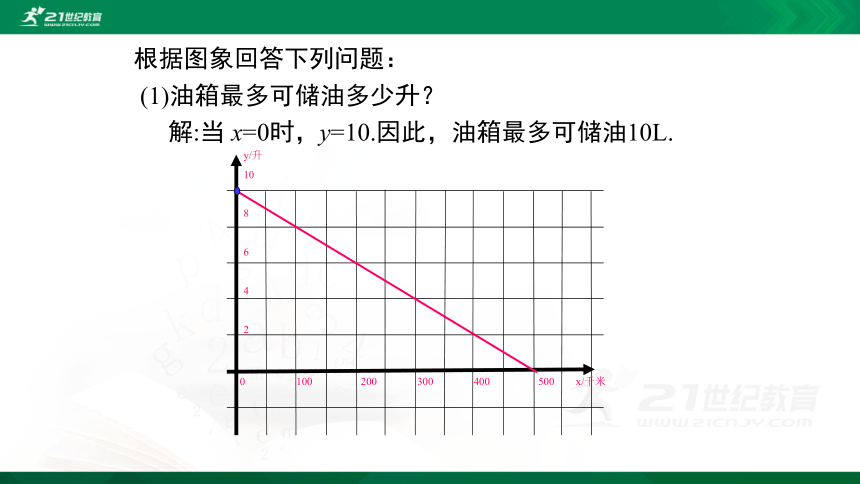
(1)油箱最多可储油多少升?
解:当 x=0时,y=10.因此,油箱最多可储油10L.
根据图象回答下列问题:
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
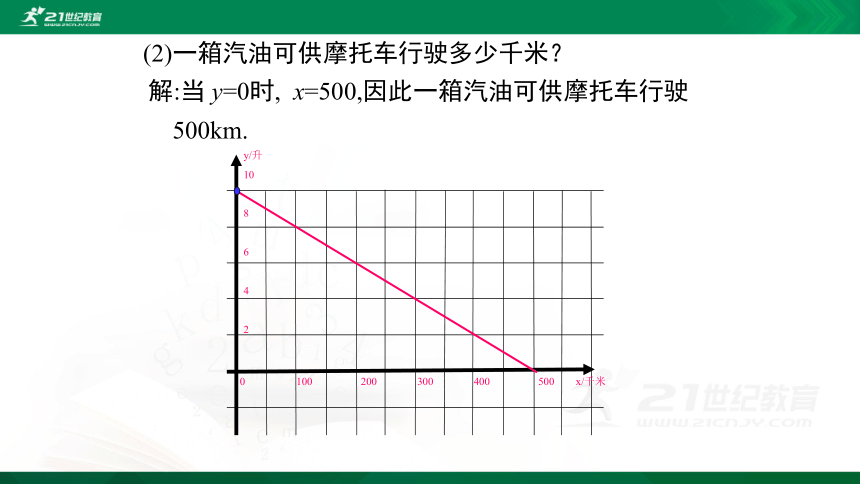
(2)一箱汽油可供摩托车行驶多少千米?
解:当 y=0时, x=500,因此一箱汽油可供摩托车行驶500km.
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
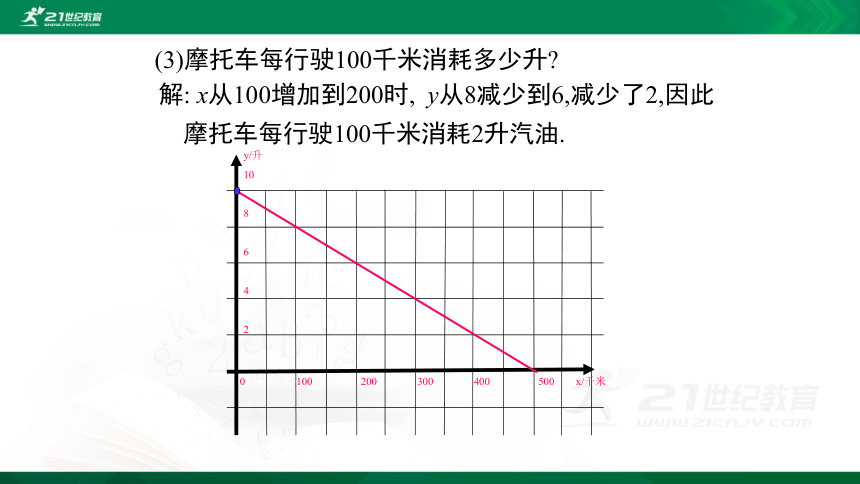
(3)摩托车每行驶100千米消耗多少升?
解: x从100增加到200时, y从8减少到6,减少了2,因此摩托车每行驶100千米消耗2升汽油.
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(4)油箱中的剩余油量小于1升时将自动报警.行驶多少千米后,摩托车 将自动报警?
解:当y=1时,x=450,因此行驶了450千米后,摩托车将自动报警.
总结归纳
如何解答实际情景函数图象的信息?
1.理解横纵坐标分别表示的的实际意义;
3.利用数形结合的思想:
将“数”转化为“形” 由“形”定“数”
2.分析已知条件,通过作x轴或y轴的垂线,在图象上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值;
原图
应用与延伸
例1中摩托车行至加油站加完油后,
摩托车油箱的剩余油量y(升)和摩托
车行驶路程x(千米)之间 的关系变为图1:
试问: ⑴加油站在多少千米处? 加油多少升?
400千米
6-2=4升
( ,6)
图1 加油后的图象
( ,2)
试问: ⑵加油前每100千米耗油多少升? 加油后每100千米耗油多少升?
(400,6)
图1 加油后的图象
(400,2)
(600,2)
解: 加油前,摩托车每行驶100千米消耗 2升汽油.
加油后 ,x从 400 增加到 600 时,油从 6 减少到 2 升,200千米用了4 升,因此摩托车每行驶100千米消耗 2 升汽油.
应用与延伸
试问: ⑶若乙地与加油站之间还有250千米,要到达乙地所加的油是否够用?
图1 加油后的图象
答:够用.
理由:由图象上观察的:400千米处设加油站,到700米处油用完,说明所加油最多可供行驶300千米.
应用与延伸
9
6
3
12
15
18
21
24
Y/cm
l
2
4
6
8
10
12
14
t/天
某植物t天后的高度为ycm,图中的l 反映了y与t之间的关系,根据图象回答下列问题:
(1)植物刚栽的时候多高?
(2)3天后该植物多高?
(3)几天后该植物高度可达
21cm?
9cm
12cm
12天
(3,12)
(12,21)
练一练
议一议:一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
1.从“数”的方面看,当一次函数y=0.5x+1的因变量的值为0时,相应的自变量的值即为方程0.5x+1=0的解.
2.从“形”的方面看,函数y=0.5x+1与x轴交点的横坐标,即为方程0.5x+1=0的解.
2
0
1
3
1
2
3
-1
-2
-3
-1
-2
-3
x
y
二、一次函数与一元一次方程
1.直线y=2x+20与x轴交点坐标为(____,____),这说明方程2x+20=0的解是x=_____.
-10
0
-10
练一练
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(____,_____).
5
0
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系
一次函数y= kx+b
中y=0时x的值.
从“函数值”看
求一元一次方程
kx+b=0的解.
求直线y= kx+b
与 x 轴交点的横
坐标.
从“函数图象”看
归纳总结
课堂练习
1.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是 ( )
A.37.2分钟 B.48分钟
C.30分钟 D.33分钟
A
课堂练习
2. 小车沿一个斜坡下滑,它的速度v(m/s)与时间t(s)的关系如图所示,v与t之间的关系式是 ,下滑3 s时小车的速度是 .
v=2.5t
7.5 m/s
课堂练习
3.如图所示的折线ABC为某地出租车收费y(元)与乘坐路程x(千米)之间的函数关系图象,当x≥3时,该函数的解析式为 ,乘坐2千米时,
车费为 元,乘坐8千米时,车费为 元.
4.一元一次方程0.5x+1=0的解是一次函数y=0.5x+1的图象与 的横坐标.
y=x
3
8
x轴交点
拓展提高
5.有一个附有进、出水管的水池,每单位时间内进、出水管的进、出水量都是一定的,设从某时刻开始,4小时内只进水不出水,在随后的时间内不进水只出水,得到时间x(时)与池内水量y(m3)之间的关系.(如图所示)
(1)进水管4小时共进多少m3水?
每小时进水多少m3?
(2)当0≤x≤4时,y与x有何关系?
(3)当x=9时,水池中的水量是多少?
拓展提高
解:(1)由图象可知,4小时共进水20m3,所以每小时进水20÷4=5(m3).
(2) y是x的正比例函数,设y=kx,由于其图象过点(4,20),
∴20=4k,k=5,即y=5x(0≤x≤4).
(3)由图象可知当x=9时,y=10,即水池中的水量为10m3.
直击中考
6.(2019?辽阳)一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;
②出发1.25h后两人相遇;
③甲每小时比乙多骑行8km;
④相遇后,乙又骑行了15min或65min时两人相距2km.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
D
直击中考
7.(2019?阜新)甲、乙两人分别从A,B两地相向而行,匀速行进甲先出发且先到达B地,他们之间的距离s(km)与甲出发的时间t(h)的关系如图所示,则乙由B地到A地用了 h.
10
课堂总结
本节课主要应掌握以下内容:
1.能通过函数图象获取信息.
2.能利用函数图象解决简单的实际问题.
3.初步体会方程与函数的关系.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.由一次函数的图象可确定k 和 b 的符号;
2.由一次函数的图象可估计函数的变化趋势;
3.可直接观察出:x与y 的对应值;
4.由一次函数的图象与y 轴的交点的坐标可确定b值,
从而确定一次函数的图象的表达式.
从一次函数图象可获得哪些信息?
第2课时 单个一次函数图象的应用
4.4 一次函数的应用
学习目标
1.掌握单个一次函数图象的应用.(重点)
2.了解一次函数与一元一次方程的关系.
(难点)
新知导入
想一想:一次函数具有什么性质?
在一次函数y=kx+b中:
当k>0时,y随x的增大而增大,
当b>0时,直线交y轴于正半轴,必过一、二、三象限;
当b<0时,直线交y轴于负半轴,必过一、三、四象限.
当k<0时,y随x的增大而减小,
当b>0时,直线交y轴于正半轴,必过一、二、四象限;
当b<0时,直线交y轴于负半轴,必过二、三、四象限.
新知导入
在前几节课里,我们通过从生活中的实际问题情景出发,分别学习了一次函数,一次函数的图象,一次函数图象的性质,从中对一次函数在现实生活中的广泛应用有了一定的了解.
怎样应用一次函数的图象和性质来解决现实生活中的实际问题,是我们这节课的主要内容.
例1:某种摩托车加满油后,油箱中的剩余油量y(升)与摩托车行驶路程x(千米)之间的关系如图所示:
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
典例解析
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(1)油箱最多可储油多少升?
解:当 x=0时,y=10.因此,油箱最多可储油10L.
根据图象回答下列问题:
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(2)一箱汽油可供摩托车行驶多少千米?
解:当 y=0时, x=500,因此一箱汽油可供摩托车行驶500km.
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(3)摩托车每行驶100千米消耗多少升?
解: x从100增加到200时, y从8减少到6,减少了2,因此摩托车每行驶100千米消耗2升汽油.
0 100 200 300 400 500 x/千米
y/升
10
8
6
4
2
(4)油箱中的剩余油量小于1升时将自动报警.行驶多少千米后,摩托车 将自动报警?
解:当y=1时,x=450,因此行驶了450千米后,摩托车将自动报警.
总结归纳
如何解答实际情景函数图象的信息?
1.理解横纵坐标分别表示的的实际意义;
3.利用数形结合的思想:
将“数”转化为“形” 由“形”定“数”
2.分析已知条件,通过作x轴或y轴的垂线,在图象上找到对应的点,由点的横坐标或者纵坐标的值读出要求的值;
原图
应用与延伸
例1中摩托车行至加油站加完油后,
摩托车油箱的剩余油量y(升)和摩托
车行驶路程x(千米)之间 的关系变为图1:
试问: ⑴加油站在多少千米处? 加油多少升?
400千米
6-2=4升
( ,6)
图1 加油后的图象
( ,2)
试问: ⑵加油前每100千米耗油多少升? 加油后每100千米耗油多少升?
(400,6)
图1 加油后的图象
(400,2)
(600,2)
解: 加油前,摩托车每行驶100千米消耗 2升汽油.
加油后 ,x从 400 增加到 600 时,油从 6 减少到 2 升,200千米用了4 升,因此摩托车每行驶100千米消耗 2 升汽油.
应用与延伸
试问: ⑶若乙地与加油站之间还有250千米,要到达乙地所加的油是否够用?
图1 加油后的图象
答:够用.
理由:由图象上观察的:400千米处设加油站,到700米处油用完,说明所加油最多可供行驶300千米.
应用与延伸
9
6
3
12
15
18
21
24
Y/cm
l
2
4
6
8
10
12
14
t/天
某植物t天后的高度为ycm,图中的l 反映了y与t之间的关系,根据图象回答下列问题:
(1)植物刚栽的时候多高?
(2)3天后该植物多高?
(3)几天后该植物高度可达
21cm?
9cm
12cm
12天
(3,12)
(12,21)
练一练
议一议:一元一次方程0.5x+1=0与一次函数y=0.5x+1有什么联系?
1.从“数”的方面看,当一次函数y=0.5x+1的因变量的值为0时,相应的自变量的值即为方程0.5x+1=0的解.
2.从“形”的方面看,函数y=0.5x+1与x轴交点的横坐标,即为方程0.5x+1=0的解.
2
0
1
3
1
2
3
-1
-2
-3
-1
-2
-3
x
y
二、一次函数与一元一次方程
1.直线y=2x+20与x轴交点坐标为(____,____),这说明方程2x+20=0的解是x=_____.
-10
0
-10
练一练
2.若方程kx+b=0的解是x=5,则直线y=kx+b与x轴交点坐标为(____,_____).
5
0
求一元一次方程
kx+b=0的解.
一次函数与一元一次方程的关系
一次函数y= kx+b
中y=0时x的值.
从“函数值”看
求一元一次方程
kx+b=0的解.
求直线y= kx+b
与 x 轴交点的横
坐标.
从“函数图象”看
归纳总结
课堂练习
1.小明早晨从家骑车到学校,先上坡后下坡,行程情况如图所示.若返回时上坡、下坡的速度仍保持不变,那么小明从学校骑车回家用的时间是 ( )
A.37.2分钟 B.48分钟
C.30分钟 D.33分钟
A
课堂练习
2. 小车沿一个斜坡下滑,它的速度v(m/s)与时间t(s)的关系如图所示,v与t之间的关系式是 ,下滑3 s时小车的速度是 .
v=2.5t
7.5 m/s
课堂练习
3.如图所示的折线ABC为某地出租车收费y(元)与乘坐路程x(千米)之间的函数关系图象,当x≥3时,该函数的解析式为 ,乘坐2千米时,
车费为 元,乘坐8千米时,车费为 元.
4.一元一次方程0.5x+1=0的解是一次函数y=0.5x+1的图象与 的横坐标.
y=x
3
8
x轴交点
拓展提高
5.有一个附有进、出水管的水池,每单位时间内进、出水管的进、出水量都是一定的,设从某时刻开始,4小时内只进水不出水,在随后的时间内不进水只出水,得到时间x(时)与池内水量y(m3)之间的关系.(如图所示)
(1)进水管4小时共进多少m3水?
每小时进水多少m3?
(2)当0≤x≤4时,y与x有何关系?
(3)当x=9时,水池中的水量是多少?
拓展提高
解:(1)由图象可知,4小时共进水20m3,所以每小时进水20÷4=5(m3).
(2) y是x的正比例函数,设y=kx,由于其图象过点(4,20),
∴20=4k,k=5,即y=5x(0≤x≤4).
(3)由图象可知当x=9时,y=10,即水池中的水量为10m3.
直击中考
6.(2019?辽阳)一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;
②出发1.25h后两人相遇;
③甲每小时比乙多骑行8km;
④相遇后,乙又骑行了15min或65min时两人相距2km.
其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
D
直击中考
7.(2019?阜新)甲、乙两人分别从A,B两地相向而行,匀速行进甲先出发且先到达B地,他们之间的距离s(km)与甲出发的时间t(h)的关系如图所示,则乙由B地到A地用了 h.
10
课堂总结
本节课主要应掌握以下内容:
1.能通过函数图象获取信息.
2.能利用函数图象解决简单的实际问题.
3.初步体会方程与函数的关系.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
