北师大版九年级数学下册1.4解直角三角形同步测试(word版含答案)
文档属性
| 名称 | 北师大版九年级数学下册1.4解直角三角形同步测试(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 341.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 11:05:47 | ||
图片预览

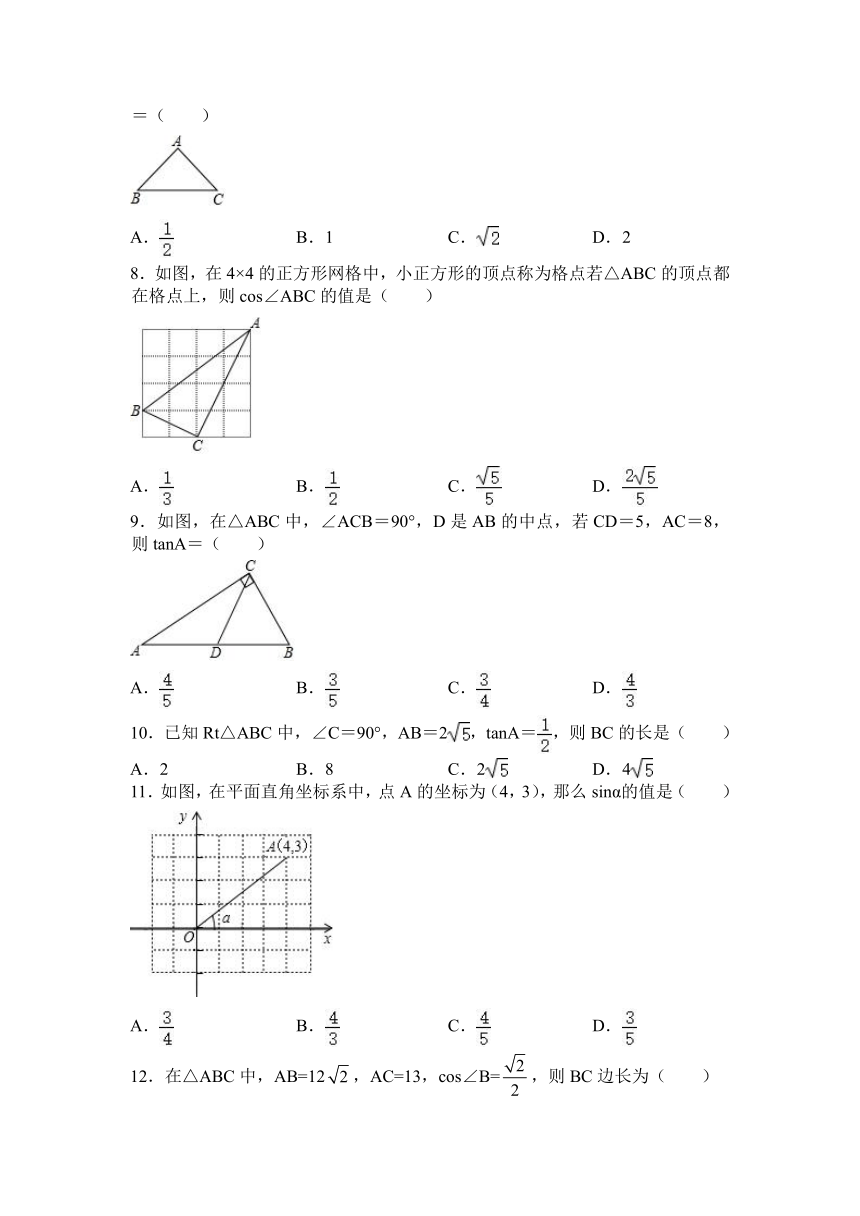


文档简介
北师大版九年级数学下册第一章1.4解直角三角形
同步测试
一.选择题
1.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴的夹角α的余切值是( )
A.
B.
C.
D.
2.
如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3
B.1,1,
C.1,1,
D.1,2,
3.等腰三角形底边与底边上的高的比是2:,则顶角为( )
A.60°
B.90°
C.120°
D.150°
4.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.
D.
5.
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBC=,则AD的长为( )
A.2
B.4
C.
D.
6.
在Rt△ABC中,∠C=Rt∠,若BC:AC=3:4,BD平分∠ABC交AC于点D,则tan∠DBC的值为( )
A.
B.
C.
D.
7.定义:在等腰三角形中,底边与腰的比叫做顶角的正对,顶角A的正对记作sadA,即sadA=底边:腰.如图,在△ABC中,AB=AC,∠A=2∠B.则sinB?sadA=( )
A.
B.1
C.
D.2
8.如图,在4×4的正方形网格中,小正方形的顶点称为格点若△ABC的顶点都在格点上,则cos∠ABC的值是( )
A.
B.
C.
D.
9.如图,在△ABC中,∠ACB=90°,D是AB的中点,若CD=5,AC=8,则tanA=( )
A.
B.
C.
D.
10.已知Rt△ABC中,∠C=90°,AB=2,tanA=,则BC的长是( )
A.2
B.8
C.2
D.4
11.如图,在平面直角坐标系中,点A的坐标为(4,3),那么sinα的值是( )
A.
B.
C.
D.
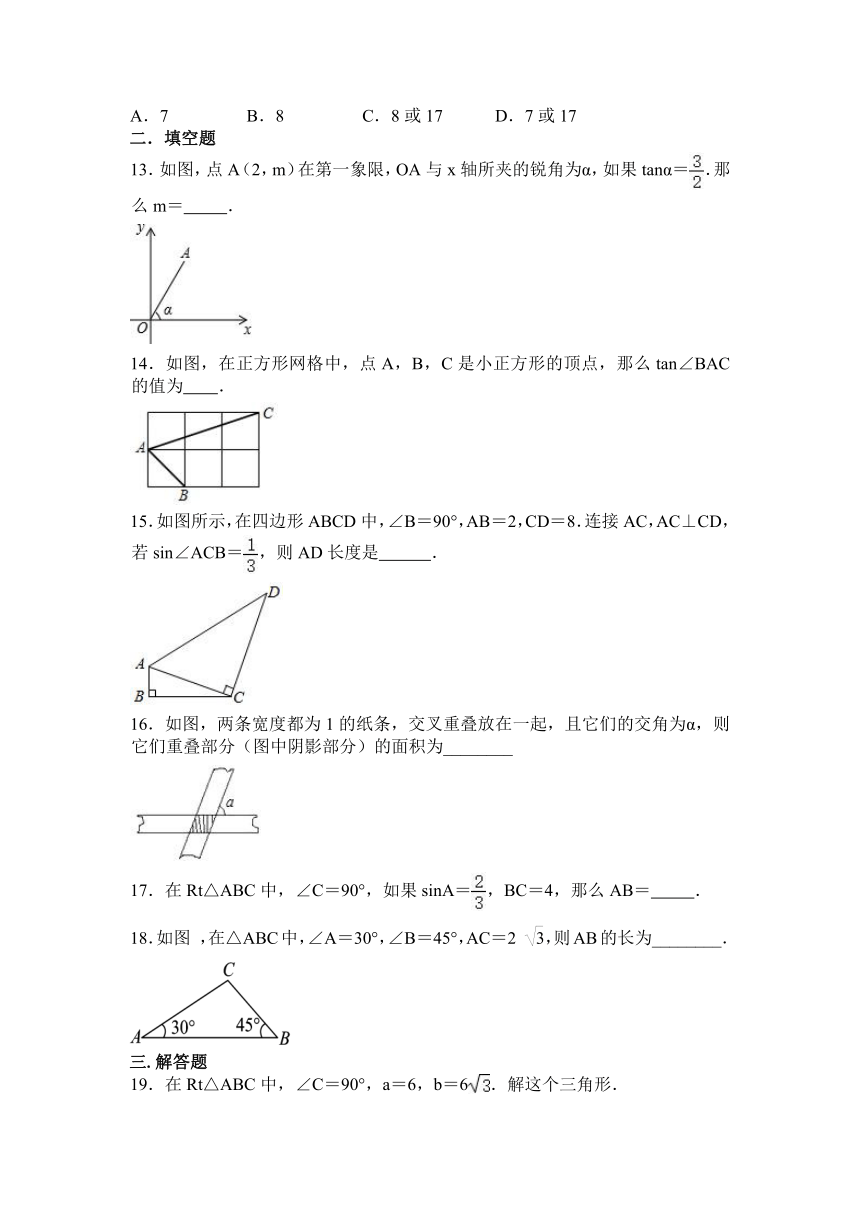
12.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7
B.8
C.8或17
D.7或17
二.填空题
13.如图,点A(2,m)在第一象限,OA与x轴所夹的锐角为α,如果tanα=.那么m=
.
14.如图,在正方形网格中,点A,B,C是小正方形的顶点,那么tan∠BAC的值为 .
15.如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB=,则AD长度是
.
16.如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为________
17.在Rt△ABC中,∠C=90°,如果sinA=,BC=4,那么AB=
.
18.如图
,在△ABC中,∠A=30°,∠B=45°,AC=2
,则AB的长为________.
三.解答题
19.在Rt△ABC中,∠C=90°,a=6,b=6.解这个三角形.
20.如图示,在△ABC中,AC=8,∠A=30°,∠B=45°,求△ABC的面积.
21.若等腰三角形两边为4,10,求底角的正弦值
22.如图,在△ABC中,∠B=90°,,D是AB上的一点,连接DC,若∠BDC=60°,BD=.试求AC的长.
23.如图,已知△ABC中,∠ABC=30°,∠ACB=45°,AB=8.求△ABC的面积.
24.已知Rt△ABC在直角坐标系中的位置如图所示,求A,C两点的坐标.
25.如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC,求sin∠BAC和点B到直线MC的距离.
26.如图,在直角坐标系中,点A,B分别在x轴、y轴上,点A的坐标为(-1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.如果PQ=,那么当点P运动一周时,点Q运动的总路程为________.
答案提示
1.B.2.D.3.A.4.D.5.A.
6.解:作DE⊥AB于E,
在Rt△ABC中,设BC为3x,则AC为4x,
根据勾股定理,AB=5x,
设CD为a,
BD平分∠ABC,则DE=CD=a,
AD=4x-a,AE=5x-3x=2x,
在Rt△ADE中,
AD2=DE2+AE2,
即(4x-a)2=a2+(2x)2,
解得,a=x,
tan∠DBC=
故选:B.
7.B.8.C.9.C.10.A.11.D.
12.解:
∵cos∠B=,∴∠B=45°,
当△ABC为钝角三角形时,如图1,
∵AB=12,∠B=45°,
∴AD=BD=12,
∵AC=13,
∴由勾股定理得CD=5,
∴BC=BD-CD=12-5=7;
当△ABC为锐角三角形时,如图2,
BC=BD+CD=12=5=17,
故选D.
13.3.
14.2.
15.10.
16.
.
17.6.
18.3+
19.解:由勾股定理得,c====12,
∵tanA===,
∴∠A=30°,
∴∠B=90°﹣∠A=90°﹣30°=60°,
即:c=12,∠A=30°,∠B=60°;
20.解:如图,
过点C作CD⊥AB,垂足为D,
在Rt△ACD中,AC=8,∠A=30°,
∴CD=4,AD=4.
在Rt△BCD中,CD=4,∠B=45°,
∴BD=CD=4,
∴AB=4+4,
∴S△ABC=AB?CD
=×4×(4+4)
=8+8.
答:△ABC的面积为8+8.
21.解:
∵4+4=8<10,
∴AB=AC=10,BC=4.
过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BD=DC=BC=2.
∵AB=AC=10,
∴AD=
∴sin∠ABD=
解:在△ABC中,∠B=90°,,
∴.
设:AB=5x,AC=7x,
由勾股定理
得,
在Rt△DBC中,∠BDC=60°,BD=2,
∴BC=BDtan60°=2×=6,
∴2x=6,
解得
x=,
∴AC=7x=.
23.解:作AD⊥BC于点D,
在Rt△ABD中,∠ABC=30°,
∴AD=AB=4,BD=AB?cos∠ABC=4,
在Rt△ACD中,∠ACB=45°,
∴CD=AD=4,
∴BC=BD+CD=4+4,
∴△ABC的面积=×BC×AD=×(4+4)×4=8+8.
24.解:如图所示,过点A作AD⊥BC于点D,
∵BC===4,
∴点C的坐标为(4,0).
在Rt△ABD中,sin30°=,cos30°=,而AO=2
,
∴AD=AOsin30°=2
×=,
BD=AOcos30°=2
×=3,
∴点A的坐标为(3,).
25.解:如图,过点B作BE⊥MC,垂足为E,
在Rt△ABC中,BC==
=5,
sin∠BAC==.
在Rt△BEC中,BE=BC·sin∠BCE=BC·sin∠BAC,
∴BE=5×=,
即点B到直线MC的距离是.
解:
在Rt△AOB中,∵∠ABO=30°,AO=1,
∴AB=2,BO==.
(1)当点P从O→B时,如图①、图②所示,点Q运动的路程为;
(2)当点P从B→C时,如图③所示,这时QC⊥AB,则∠ACQ=90°.
∵∠ABO=30°,∴∠BAO=60°,
∴∠OQD=90°-60°=30°,
∴cos30°=,∴AQ==2,
∴OQ=2-1=1.则点Q运动的路程为QO=1;
(3)当点P从C→A时,如图③所示,点Q运动的路程为QQ′=2-.
(4)当点P从A→O时,点Q运动的路程为AO=1.
∴点Q运动的总路程为+1+2-+1=4.
同步测试
一.选择题
1.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴的夹角α的余切值是( )
A.
B.
C.
D.
2.
如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A.1,2,3
B.1,1,
C.1,1,
D.1,2,
3.等腰三角形底边与底边上的高的比是2:,则顶角为( )
A.60°
B.90°
C.120°
D.150°
4.如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA的值为( )
A.
B.
C.
D.
5.
如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBC=,则AD的长为( )
A.2
B.4
C.
D.
6.
在Rt△ABC中,∠C=Rt∠,若BC:AC=3:4,BD平分∠ABC交AC于点D,则tan∠DBC的值为( )
A.
B.
C.
D.
7.定义:在等腰三角形中,底边与腰的比叫做顶角的正对,顶角A的正对记作sadA,即sadA=底边:腰.如图,在△ABC中,AB=AC,∠A=2∠B.则sinB?sadA=( )
A.
B.1
C.
D.2
8.如图,在4×4的正方形网格中,小正方形的顶点称为格点若△ABC的顶点都在格点上,则cos∠ABC的值是( )
A.
B.
C.
D.
9.如图,在△ABC中,∠ACB=90°,D是AB的中点,若CD=5,AC=8,则tanA=( )
A.
B.
C.
D.
10.已知Rt△ABC中,∠C=90°,AB=2,tanA=,则BC的长是( )
A.2
B.8
C.2
D.4
11.如图,在平面直角坐标系中,点A的坐标为(4,3),那么sinα的值是( )
A.
B.
C.
D.
12.在△ABC中,AB=12,AC=13,cos∠B=,则BC边长为( )
A.7
B.8
C.8或17
D.7或17
二.填空题
13.如图,点A(2,m)在第一象限,OA与x轴所夹的锐角为α,如果tanα=.那么m=
.
14.如图,在正方形网格中,点A,B,C是小正方形的顶点,那么tan∠BAC的值为 .
15.如图所示,在四边形ABCD中,∠B=90°,AB=2,CD=8.连接AC,AC⊥CD,若sin∠ACB=,则AD长度是
.
16.如图,两条宽度都为1的纸条,交叉重叠放在一起,且它们的交角为α,则它们重叠部分(图中阴影部分)的面积为________
17.在Rt△ABC中,∠C=90°,如果sinA=,BC=4,那么AB=
.
18.如图
,在△ABC中,∠A=30°,∠B=45°,AC=2
,则AB的长为________.
三.解答题
19.在Rt△ABC中,∠C=90°,a=6,b=6.解这个三角形.
20.如图示,在△ABC中,AC=8,∠A=30°,∠B=45°,求△ABC的面积.
21.若等腰三角形两边为4,10,求底角的正弦值
22.如图,在△ABC中,∠B=90°,,D是AB上的一点,连接DC,若∠BDC=60°,BD=.试求AC的长.
23.如图,已知△ABC中,∠ABC=30°,∠ACB=45°,AB=8.求△ABC的面积.
24.已知Rt△ABC在直角坐标系中的位置如图所示,求A,C两点的坐标.
25.如图,∠ACB=90°,AB=13,AC=12,∠BCM=∠BAC,求sin∠BAC和点B到直线MC的距离.
26.如图,在直角坐标系中,点A,B分别在x轴、y轴上,点A的坐标为(-1,0),∠ABO=30°,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在x轴的非负半轴上运动.如果PQ=,那么当点P运动一周时,点Q运动的总路程为________.
答案提示
1.B.2.D.3.A.4.D.5.A.
6.解:作DE⊥AB于E,
在Rt△ABC中,设BC为3x,则AC为4x,
根据勾股定理,AB=5x,
设CD为a,
BD平分∠ABC,则DE=CD=a,
AD=4x-a,AE=5x-3x=2x,
在Rt△ADE中,
AD2=DE2+AE2,
即(4x-a)2=a2+(2x)2,
解得,a=x,
tan∠DBC=
故选:B.
7.B.8.C.9.C.10.A.11.D.
12.解:
∵cos∠B=,∴∠B=45°,
当△ABC为钝角三角形时,如图1,
∵AB=12,∠B=45°,
∴AD=BD=12,
∵AC=13,
∴由勾股定理得CD=5,
∴BC=BD-CD=12-5=7;
当△ABC为锐角三角形时,如图2,
BC=BD+CD=12=5=17,
故选D.
13.3.
14.2.
15.10.
16.
.
17.6.
18.3+
19.解:由勾股定理得,c====12,
∵tanA===,
∴∠A=30°,
∴∠B=90°﹣∠A=90°﹣30°=60°,
即:c=12,∠A=30°,∠B=60°;
20.解:如图,
过点C作CD⊥AB,垂足为D,
在Rt△ACD中,AC=8,∠A=30°,
∴CD=4,AD=4.
在Rt△BCD中,CD=4,∠B=45°,
∴BD=CD=4,
∴AB=4+4,
∴S△ABC=AB?CD
=×4×(4+4)
=8+8.
答:△ABC的面积为8+8.
21.解:
∵4+4=8<10,
∴AB=AC=10,BC=4.
过点A作AD⊥BC于点D.
∵AB=AC,AD⊥BC,
∴BD=DC=BC=2.
∵AB=AC=10,
∴AD=
∴sin∠ABD=
解:在△ABC中,∠B=90°,,
∴.
设:AB=5x,AC=7x,
由勾股定理
得,
在Rt△DBC中,∠BDC=60°,BD=2,
∴BC=BDtan60°=2×=6,
∴2x=6,
解得
x=,
∴AC=7x=.
23.解:作AD⊥BC于点D,
在Rt△ABD中,∠ABC=30°,
∴AD=AB=4,BD=AB?cos∠ABC=4,
在Rt△ACD中,∠ACB=45°,
∴CD=AD=4,
∴BC=BD+CD=4+4,
∴△ABC的面积=×BC×AD=×(4+4)×4=8+8.
24.解:如图所示,过点A作AD⊥BC于点D,
∵BC===4,
∴点C的坐标为(4,0).
在Rt△ABD中,sin30°=,cos30°=,而AO=2
,
∴AD=AOsin30°=2
×=,
BD=AOcos30°=2
×=3,
∴点A的坐标为(3,).
25.解:如图,过点B作BE⊥MC,垂足为E,
在Rt△ABC中,BC==
=5,
sin∠BAC==.
在Rt△BEC中,BE=BC·sin∠BCE=BC·sin∠BAC,
∴BE=5×=,
即点B到直线MC的距离是.
解:
在Rt△AOB中,∵∠ABO=30°,AO=1,
∴AB=2,BO==.
(1)当点P从O→B时,如图①、图②所示,点Q运动的路程为;
(2)当点P从B→C时,如图③所示,这时QC⊥AB,则∠ACQ=90°.
∵∠ABO=30°,∴∠BAO=60°,
∴∠OQD=90°-60°=30°,
∴cos30°=,∴AQ==2,
∴OQ=2-1=1.则点Q运动的路程为QO=1;
(3)当点P从C→A时,如图③所示,点Q运动的路程为QQ′=2-.
(4)当点P从A→O时,点Q运动的路程为AO=1.
∴点Q运动的总路程为+1+2-+1=4.
