1.5三角函数的应用-北师大版九年级数学下册同步测试(Word版含答案)
文档属性
| 名称 | 1.5三角函数的应用-北师大版九年级数学下册同步测试(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 450.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 10:50:51 | ||
图片预览




文档简介
北师大版九年级数学下册第一章1.5三角函数的应用
同步测试
一.选择题
1.如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
A.12m
B.3m
C.4m
D.12m
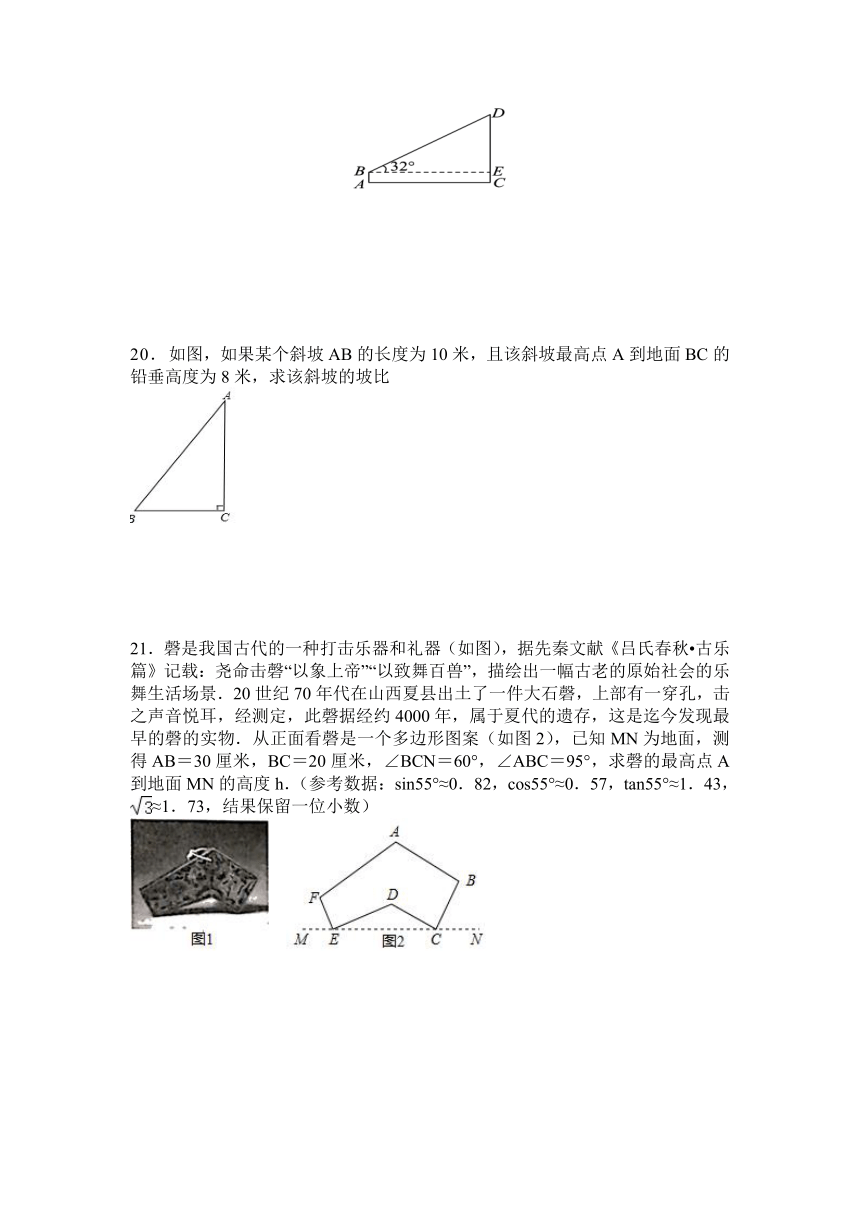
2.如图,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形.如果用彩色胶带如图包扎礼盒,所需胶带长度至少为多少?(参考数据:≈1.414,≈1.732,≈2.236)( )
A.320cm
B.395.24
cm
C.431.76
cm
D.480
cm
3.如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A.
B.
C.6cos50°
D.
4.身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300m,250m,200m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( )
A.甲的最高
B.乙的最低
C.丙的最低
D.乙的最高
5.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米
B.6米
C.8米
D.(3+)米
6.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米
B.10米
C.10米
D.20米
7.如图,坡角为27°的斜坡上两根电线杆间的坡面距离为80米,则这两根电线杆间的水平距离为( )
A.米
B.80cos27°米
C.80tan27°米
D.米
8.
一斜坡长为米,高度为1米,那么坡比为( )
A.1:3
B.1:
C.1:
D.1:
9.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
B.
C.
D.
10.
拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是( )
A.15m
B.20m
C.10m
D.20m
11.若小王沿坡度i=3:4的斜坡向上行走10m,则他所在的位置比原来的位置升高了( )
A.3m
B.4m
C.6m
D.8m
12.在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如图,线段BC表示无障碍通道,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)为i=1:2,BC=12米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
A.10
B.10﹣12
C.12
D.10+12
二.填空题
13.如图,在坡度为1:3的山坡上种树,要求株距(相邻两树间的水平距离)是6米,则斜坡上相邻两树间的坡面距离是_________米(结果保留根号)
14.如图,一辆小车沿着坡度为i=1:的斜坡从点A向上行驶了50米到点B处,则此时该小车离水平面的垂直高度为
.
15.如图,两根竹竿AB和AD斜靠在棱CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为 .
16.圭表是度量日影长度的一种天文仪器,由“圭”和“表”两个部件组成,垂直于地面的直杆叫“表”,水平放置于地面且刻有刻度以测量影长的标尺叫“圭”.如图是小彬根据学校所在地理位置设计的圭表示意图,其中冬至时正午阳光入射角∠ABC=28.8°,夏至时正午阳光入射角∠ADC=75.8°.已知“表”高AC=20cm,则“圭”上所刻冬至线与夏至线之间的距离BD约为
cm.(精确到lcm;参考数据:cos75.8°≈0.2,tan75.8°≈4.0,cos28.8°≈0.9,tan28.8°=0.5)
17.如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是6m,则乘电梯从点B到点C上升的高度h是_________.
18.如图是一个仰卧起坐健身器侧面示意图,AC、BC是支架,OC是坐垫,OD为靠背(可绕点O旋转),OA=OD=900mm,∠BAC=20°,当α=40°时,点D到地面的距离为
mm.(sin20°=0.34,cos20°=0.94,tan20°=0.36,sin40°=0.64,cos40°=0.77)
19.某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5
m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20
m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
20.如图,如果某个斜坡AB的长度为10米,且该斜坡最高点A到地面BC的铅垂高度为8米,求该斜坡的坡比
21.磬是我国古代的一种打击乐器和礼器(如图),据先秦文献《吕氏春秋?古乐篇》记载:尧命击磬“以象上帝”“以致舞百兽”,描绘出一幅古老的原始社会的乐舞生活场景.20世纪70年代在山西夏县出土了一件大石磬,上部有一穿孔,击之声音悦耳,经测定,此磬据经约4000年,属于夏代的遗存,这是迄今发现最早的磬的实物.从正面看磬是一个多边形图案(如图2),已知MN为地面,测得AB=30厘米,BC=20厘米,∠BCN=60°,∠ABC=95°,求磬的最高点A到地面MN的高度h.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,≈1.73,结果保留一位小数)
22.如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
23.如图1是放置在水平面上的台灯,图2是其侧面示意图(台灯底座高度忽略),其中灯臂AC=20cm,灯臂CD=58cm,灯臂与底座构成∠CAB=127°,灯臂AC与灯臂CD构成的∠DCA=113°,求灯臂与灯罩连接处点D与桌面AB的距离?(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,≈1.73).
24.某校一棵大树发生一定的倾斜,该树与地面的夹角∠ABC=75°.小明测得某时大树的影子顶端在地面C处,此时光线与地面的夹角∠ACB=30°;又过了一段时间,测得大树的影子顶端在地面D处,此时光线与地面的夹角∠ADB=50°.若CD=8米,求该树倾斜前的高度(即AB的长度).(结果保留一位小数.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,≈1.73)
25.在某飞机场东西方向的地面l上有一长为1
km的飞机跑道MN(如图),在跑道MN的正西端14.5
km处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15
km的B处;经过1
min,又测得该飞机位于点A的北偏东60°,且与点A相距5
km的C处.
(1)该飞机航行的速度是多少km/h?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
26.如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α要满足60°≤α≤75°,现有一架长5.5m的梯子.
(1)使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?
(2)当梯子底端距离墙面2.2m时,α等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?
(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,sin23.6°≈0.40,cos66.4°≈0.40,tan21.8°≈0.40.)
答案提示
1.C.2.C.3.D.4.D.5.A.6.C.7.B.8.A.9.A.10D.11.C.
12.解:如图,延长AB交DC的延长线于点E,
,
由BC的坡度(或坡比)为i=1:2,得BE:CE=1:2.
设BE=x米,CE=2x米.
在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,
即x2+(2x)2=(12)2,
解得x=12(米),
∴BE=12(米),CE=24(米),
DE=DC+CE=6+24=30(米),
由tan30°=,得
,
解得AE=10(米).
由线段的和差,得
AB=AE﹣BE=(10﹣12)(米),
故选:B.
13.米.
14.25米.15..16.35.17.6.
18.解:连接AD,过点O作OH⊥AD于H,
∵OA=OD=900mm,OH⊥AD,α=40°
∴∠AOH=∠AOD=20°,AH=DH,
∵∠BAC=20°,
∴∠BAC=∠AOH,
∴OH∥AB,
∴AD⊥AB,
在Rt△AOH中,OA=900mm,sin∠AOH=,
∴AH=OA?sin20°=900×0.34=306
(mm),
∴AD=2AH=612(mm),
故答案为:612.
19.解:由题意得AC=20
m,AB=1.5
m.
∵在Rt△DBE中,∠DBE=32°,
BE=AC=20
m,
∴DE=BEtan32°≈20×0.62=12.4(m),
∴CD=DE+CE=DE+AB≈12.4+1.5=13.9(m).
答:旗杆CD的高度约为13.9
m.
20.解:∵某个斜坡AB的长度为10米,且该斜坡最高点A到地面BC的铅垂高度为8米,∴水平距离BC=
=6(m),
则该斜坡的坡比是:
故答案为:
21.解:过A作AG⊥MN于点G,过点B作BH⊥AG于点H,作BK⊥MN于点K,
∵BC=20厘米,∠BCN=60°,
∴HG=BK=BC?sin60°=20×=10≈17.3(cm),∠HBC=∠BCK=60°,
∵∠ABC=95°,
∴∠ABH=95°﹣60°=35°,
∴∠BAH=55°,
∵AB=30厘米,
∴AH=AB?cos55°≈30×0.57=17.1(cm),
∴h=AG=AH+HG≈17.3+17.1=34.4(cm).
答:磬的最高点A到地面MN的高度h为34.4cm.
22.解:(1)过点P作PE∥MN,交B栋楼与点E,
则四边形PEMN为矩形.
∴EP=MN
由题意知:∠EPD=55.7°
∠EPC=30°.
在Rt△ECP中,EC=tan∠EPC×EP
=tan30°×EP=EP≈0.58EP,
在Rt△EDP中,ED=tan∠EPD×EP
=tan55.7°×EP≈1.47EP,
∵CD=ED﹣EC,
∴1.47EP﹣0.58EP=44.5
∴EP=MN=50(m)
答:楼间距MN为50m.
(2)∵EC=0.58EP
=0.58×50=29(m)
∴CM=90﹣29=61(m)
∵61÷3≈20.3≈21(层)
答:点C位于第21层.
23.解:如图2,过点D作DH⊥AB于H,过点C作CF⊥DH于F,过点A作AG⊥CF于G,
∵∠AGF=∠GFH=∠AHF=90°,
∴四边形AEFG是矩形,
∴∠HAG=90°,
∴HF=AG,
∵∠CAB=127°,
∴∠CAG=∠CAB﹣∠HAG=37°,
在Rt△CAG中,
AG=AC?cos∠CAG=20×cos37°≈16(cm),
∴HF≈16(cm),
∵∠ACG=90°﹣∠CAG=53°,
∴∠DCF=∠ACD﹣∠ACG=113°﹣53°=60°,
在Rt△DCF中,
DF=CDsin∠DCF=58×sin60°≈50.17(cm),
∴HD=DF+HF≈50.17+16≈66.2(cm).
故灯臂与灯罩连接处点D与桌面AB的距离约为66.2cm.
24.解:过A作AH⊥BC于H,
在Rt△ACH中,∵∠C=30°,
∴tan30°=,
∴CH==AH,
在Rt△ADH中,∵∠ADH=50°,
∴tan∠ADH=≈1.19,
∴DH=,
∵CD=CH﹣DH=AH﹣AH=8,
∴AH≈8.99,
在Rt△AHB中,∵∠B=75°,
∴sin75°=,
∴AB=≈8.99÷0.97≈9.3米,
答:该树倾斜前的高度是9.3米.
25.解:
(1)由题意,得∠BAC=90°,AB=15
km,AC=5
km,
∴BC==10
(km),
∴飞机航行的速度为10
÷=600
(km/h).
(2)能.理由如下:
如图,过点C作CE⊥l于点E,设直线BC交l于点F.
在Rt△ABC中,AC=5
km,BC=10
km,
∴∠ABC=30°,即∠BCA=60°.
又∵∠CAE=30°,∴∠ACE=∠FCE=60°,
∴CE=AC·sin∠CAE=
km,
AE=AC·cos∠CAE=
km.
则AF=2AE=15
km.
∵AN=AM+MN=14.5+1=15.5(km),
∴AM<AF<AN,
∴飞机不改变航向继续航行,可以降落在跑道MN之间.
26.解:(1)由题意得,当α=75°时,这架梯子可以安全攀上最高的墙,
在Rt△ABC中,sinα=,
∴AC=AB?sinα≈5.5×0.97≈5.3,
答:使用这架梯子最高可以安全攀上约5.3m的墙;
(2)在Rt△ABC中,cosα===0.4,
则α≈66.4°,
∵60°<66.4°<75°,
∴此时人能够安全使用这架梯子.
同步测试
一.选择题
1.如图,在坡角为30°的斜坡上要栽两棵树,要求它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为( )
A.12m
B.3m
C.4m
D.12m
2.如图,上下底面为全等的正六边形礼盒,其主视图与左视图均由矩形构成,主视图中大矩形边长如图所示,左视图中包含两全等的矩形.如果用彩色胶带如图包扎礼盒,所需胶带长度至少为多少?(参考数据:≈1.414,≈1.732,≈2.236)( )
A.320cm
B.395.24
cm
C.431.76
cm
D.480
cm
3.如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
A.
B.
C.6cos50°
D.
4.身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300m,250m,200m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝( )
A.甲的最高
B.乙的最低
C.丙的最低
D.乙的最高
5.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
A.5米
B.6米
C.8米
D.(3+)米
6.某长江大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索BD与水平桥面的夹角是60°,两拉索底端距离AD=20米,则立柱BC的高为( )
A.20米
B.10米
C.10米
D.20米
7.如图,坡角为27°的斜坡上两根电线杆间的坡面距离为80米,则这两根电线杆间的水平距离为( )
A.米
B.80cos27°米
C.80tan27°米
D.米
8.
一斜坡长为米,高度为1米,那么坡比为( )
A.1:3
B.1:
C.1:
D.1:
9.某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.
B.
C.
D.
10.
拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是( )
A.15m
B.20m
C.10m
D.20m
11.若小王沿坡度i=3:4的斜坡向上行走10m,则他所在的位置比原来的位置升高了( )
A.3m
B.4m
C.6m
D.8m
12.在商场里,为方便一部分残疾人出入,商场特意设计了一种特殊通道“无障碍通道”,如图,线段BC表示无障碍通道,线段AD表示普通扶梯,其中“无障碍通道”BC的坡度(或坡比)为i=1:2,BC=12米,CD=6米,∠D=30°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.
A.10
B.10﹣12
C.12
D.10+12
二.填空题
13.如图,在坡度为1:3的山坡上种树,要求株距(相邻两树间的水平距离)是6米,则斜坡上相邻两树间的坡面距离是_________米(结果保留根号)
14.如图,一辆小车沿着坡度为i=1:的斜坡从点A向上行驶了50米到点B处,则此时该小车离水平面的垂直高度为
.
15.如图,两根竹竿AB和AD斜靠在棱CE上,量得∠ABC=α,∠ADC=β,则竹竿AB与AD的长度之比为 .
16.圭表是度量日影长度的一种天文仪器,由“圭”和“表”两个部件组成,垂直于地面的直杆叫“表”,水平放置于地面且刻有刻度以测量影长的标尺叫“圭”.如图是小彬根据学校所在地理位置设计的圭表示意图,其中冬至时正午阳光入射角∠ABC=28.8°,夏至时正午阳光入射角∠ADC=75.8°.已知“表”高AC=20cm,则“圭”上所刻冬至线与夏至线之间的距离BD约为
cm.(精确到lcm;参考数据:cos75.8°≈0.2,tan75.8°≈4.0,cos28.8°≈0.9,tan28.8°=0.5)
17.如图是石景山当代商场地下广场到地面广场的手扶电梯示意图.其中AB、CD分别表示地下广场、地面广场电梯口处的水平线.已知∠ABC=135°,BC的长约是6m,则乘电梯从点B到点C上升的高度h是_________.
18.如图是一个仰卧起坐健身器侧面示意图,AC、BC是支架,OC是坐垫,OD为靠背(可绕点O旋转),OA=OD=900mm,∠BAC=20°,当α=40°时,点D到地面的距离为
mm.(sin20°=0.34,cos20°=0.94,tan20°=0.36,sin40°=0.64,cos40°=0.77)
19.某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5
m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20
m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
20.如图,如果某个斜坡AB的长度为10米,且该斜坡最高点A到地面BC的铅垂高度为8米,求该斜坡的坡比
21.磬是我国古代的一种打击乐器和礼器(如图),据先秦文献《吕氏春秋?古乐篇》记载:尧命击磬“以象上帝”“以致舞百兽”,描绘出一幅古老的原始社会的乐舞生活场景.20世纪70年代在山西夏县出土了一件大石磬,上部有一穿孔,击之声音悦耳,经测定,此磬据经约4000年,属于夏代的遗存,这是迄今发现最早的磬的实物.从正面看磬是一个多边形图案(如图2),已知MN为地面,测得AB=30厘米,BC=20厘米,∠BCN=60°,∠ABC=95°,求磬的最高点A到地面MN的高度h.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,≈1.73,结果保留一位小数)
22.如图,某小区A栋楼在B栋楼的南侧,两楼高度均为90m,楼间距为MN.春分日正午,太阳光线与水平面所成的角为55.7°,A栋楼在B栋楼墙面上的影高为DM;冬至日正午,太阳光线与水平面所成的角为30°,A栋楼在B栋楼墙面上的影高为CM.已知CD=44.5m.
(1)求楼间距MN;
(2)若B号楼共30层,每层高均为3m,则点C位于第几层?(参考数据:tan30°≈0.58,sin55.7°≈0.83,cos55.7°≈0.56,tan55.7°≈1.47)
23.如图1是放置在水平面上的台灯,图2是其侧面示意图(台灯底座高度忽略),其中灯臂AC=20cm,灯臂CD=58cm,灯臂与底座构成∠CAB=127°,灯臂AC与灯臂CD构成的∠DCA=113°,求灯臂与灯罩连接处点D与桌面AB的距离?(结果精确到0.1cm,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,≈1.73).
24.某校一棵大树发生一定的倾斜,该树与地面的夹角∠ABC=75°.小明测得某时大树的影子顶端在地面C处,此时光线与地面的夹角∠ACB=30°;又过了一段时间,测得大树的影子顶端在地面D处,此时光线与地面的夹角∠ADB=50°.若CD=8米,求该树倾斜前的高度(即AB的长度).(结果保留一位小数.参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19,sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,≈1.73)
25.在某飞机场东西方向的地面l上有一长为1
km的飞机跑道MN(如图),在跑道MN的正西端14.5
km处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15
km的B处;经过1
min,又测得该飞机位于点A的北偏东60°,且与点A相距5
km的C处.
(1)该飞机航行的速度是多少km/h?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
26.如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角α要满足60°≤α≤75°,现有一架长5.5m的梯子.
(1)使用这架梯子最高可以安全攀上多高的墙(结果保留小数点后一位)?
(2)当梯子底端距离墙面2.2m时,α等于多少度(结果保留小数点后一位)?此时人是否能够安全使用这架梯子?
(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,sin23.6°≈0.40,cos66.4°≈0.40,tan21.8°≈0.40.)
答案提示
1.C.2.C.3.D.4.D.5.A.6.C.7.B.8.A.9.A.10D.11.C.
12.解:如图,延长AB交DC的延长线于点E,
,
由BC的坡度(或坡比)为i=1:2,得BE:CE=1:2.
设BE=x米,CE=2x米.
在Rt△BCE中,由勾股定理,得BE2+CE2=BC2,
即x2+(2x)2=(12)2,
解得x=12(米),
∴BE=12(米),CE=24(米),
DE=DC+CE=6+24=30(米),
由tan30°=,得
,
解得AE=10(米).
由线段的和差,得
AB=AE﹣BE=(10﹣12)(米),
故选:B.
13.米.
14.25米.15..16.35.17.6.
18.解:连接AD,过点O作OH⊥AD于H,
∵OA=OD=900mm,OH⊥AD,α=40°
∴∠AOH=∠AOD=20°,AH=DH,
∵∠BAC=20°,
∴∠BAC=∠AOH,
∴OH∥AB,
∴AD⊥AB,
在Rt△AOH中,OA=900mm,sin∠AOH=,
∴AH=OA?sin20°=900×0.34=306
(mm),
∴AD=2AH=612(mm),
故答案为:612.
19.解:由题意得AC=20
m,AB=1.5
m.
∵在Rt△DBE中,∠DBE=32°,
BE=AC=20
m,
∴DE=BEtan32°≈20×0.62=12.4(m),
∴CD=DE+CE=DE+AB≈12.4+1.5=13.9(m).
答:旗杆CD的高度约为13.9
m.
20.解:∵某个斜坡AB的长度为10米,且该斜坡最高点A到地面BC的铅垂高度为8米,∴水平距离BC=
=6(m),
则该斜坡的坡比是:
故答案为:
21.解:过A作AG⊥MN于点G,过点B作BH⊥AG于点H,作BK⊥MN于点K,
∵BC=20厘米,∠BCN=60°,
∴HG=BK=BC?sin60°=20×=10≈17.3(cm),∠HBC=∠BCK=60°,
∵∠ABC=95°,
∴∠ABH=95°﹣60°=35°,
∴∠BAH=55°,
∵AB=30厘米,
∴AH=AB?cos55°≈30×0.57=17.1(cm),
∴h=AG=AH+HG≈17.3+17.1=34.4(cm).
答:磬的最高点A到地面MN的高度h为34.4cm.
22.解:(1)过点P作PE∥MN,交B栋楼与点E,
则四边形PEMN为矩形.
∴EP=MN
由题意知:∠EPD=55.7°
∠EPC=30°.
在Rt△ECP中,EC=tan∠EPC×EP
=tan30°×EP=EP≈0.58EP,
在Rt△EDP中,ED=tan∠EPD×EP
=tan55.7°×EP≈1.47EP,
∵CD=ED﹣EC,
∴1.47EP﹣0.58EP=44.5
∴EP=MN=50(m)
答:楼间距MN为50m.
(2)∵EC=0.58EP
=0.58×50=29(m)
∴CM=90﹣29=61(m)
∵61÷3≈20.3≈21(层)
答:点C位于第21层.
23.解:如图2,过点D作DH⊥AB于H,过点C作CF⊥DH于F,过点A作AG⊥CF于G,
∵∠AGF=∠GFH=∠AHF=90°,
∴四边形AEFG是矩形,
∴∠HAG=90°,
∴HF=AG,
∵∠CAB=127°,
∴∠CAG=∠CAB﹣∠HAG=37°,
在Rt△CAG中,
AG=AC?cos∠CAG=20×cos37°≈16(cm),
∴HF≈16(cm),
∵∠ACG=90°﹣∠CAG=53°,
∴∠DCF=∠ACD﹣∠ACG=113°﹣53°=60°,
在Rt△DCF中,
DF=CDsin∠DCF=58×sin60°≈50.17(cm),
∴HD=DF+HF≈50.17+16≈66.2(cm).
故灯臂与灯罩连接处点D与桌面AB的距离约为66.2cm.
24.解:过A作AH⊥BC于H,
在Rt△ACH中,∵∠C=30°,
∴tan30°=,
∴CH==AH,
在Rt△ADH中,∵∠ADH=50°,
∴tan∠ADH=≈1.19,
∴DH=,
∵CD=CH﹣DH=AH﹣AH=8,
∴AH≈8.99,
在Rt△AHB中,∵∠B=75°,
∴sin75°=,
∴AB=≈8.99÷0.97≈9.3米,
答:该树倾斜前的高度是9.3米.
25.解:
(1)由题意,得∠BAC=90°,AB=15
km,AC=5
km,
∴BC==10
(km),
∴飞机航行的速度为10
÷=600
(km/h).
(2)能.理由如下:
如图,过点C作CE⊥l于点E,设直线BC交l于点F.
在Rt△ABC中,AC=5
km,BC=10
km,
∴∠ABC=30°,即∠BCA=60°.
又∵∠CAE=30°,∴∠ACE=∠FCE=60°,
∴CE=AC·sin∠CAE=
km,
AE=AC·cos∠CAE=
km.
则AF=2AE=15
km.
∵AN=AM+MN=14.5+1=15.5(km),
∴AM<AF<AN,
∴飞机不改变航向继续航行,可以降落在跑道MN之间.
26.解:(1)由题意得,当α=75°时,这架梯子可以安全攀上最高的墙,
在Rt△ABC中,sinα=,
∴AC=AB?sinα≈5.5×0.97≈5.3,
答:使用这架梯子最高可以安全攀上约5.3m的墙;
(2)在Rt△ABC中,cosα===0.4,
则α≈66.4°,
∵60°<66.4°<75°,
∴此时人能够安全使用这架梯子.
