沪科版八年级数学上册第14章全等三角形辅助线添加方法归纳--构造全等法(表格式 无答案)
文档属性
| 名称 | 沪科版八年级数学上册第14章全等三角形辅助线添加方法归纳--构造全等法(表格式 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 129.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览



文档简介
年级
八年级
教学内容
构造全等法
【知识归纳】
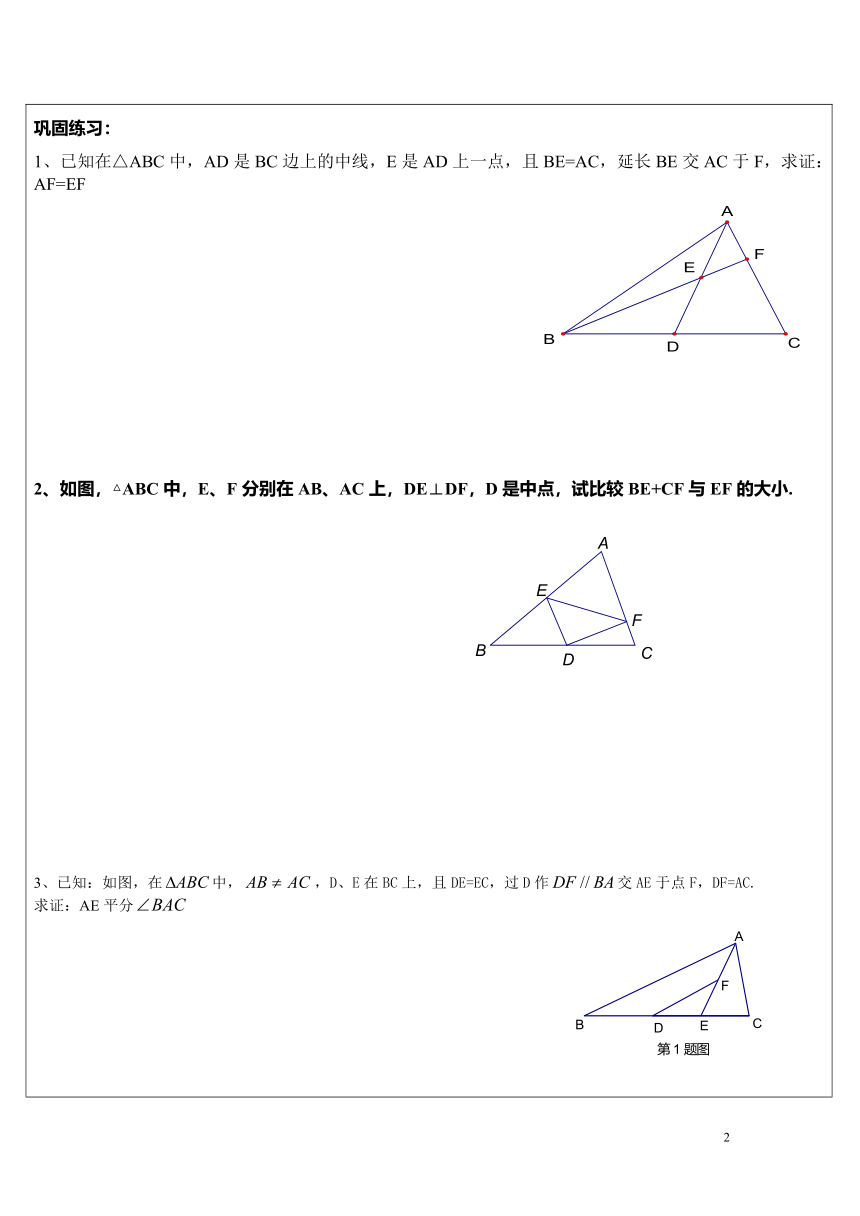
知识点一、倍长中线法:
遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”
法构造全等三角形.即把中线延长一倍,来构造全等三角形。
△ABC中
方式1:
延长AD到E,
AD是BC边中线
使DE=AD,
连接BE
方式2:间接倍长
作CF⊥AD于F,
延长MD到N,
作BE⊥AD的延长线于E
使DN=MD,
连接BE
连接CD
1、已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________.
2、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
巩固练习:
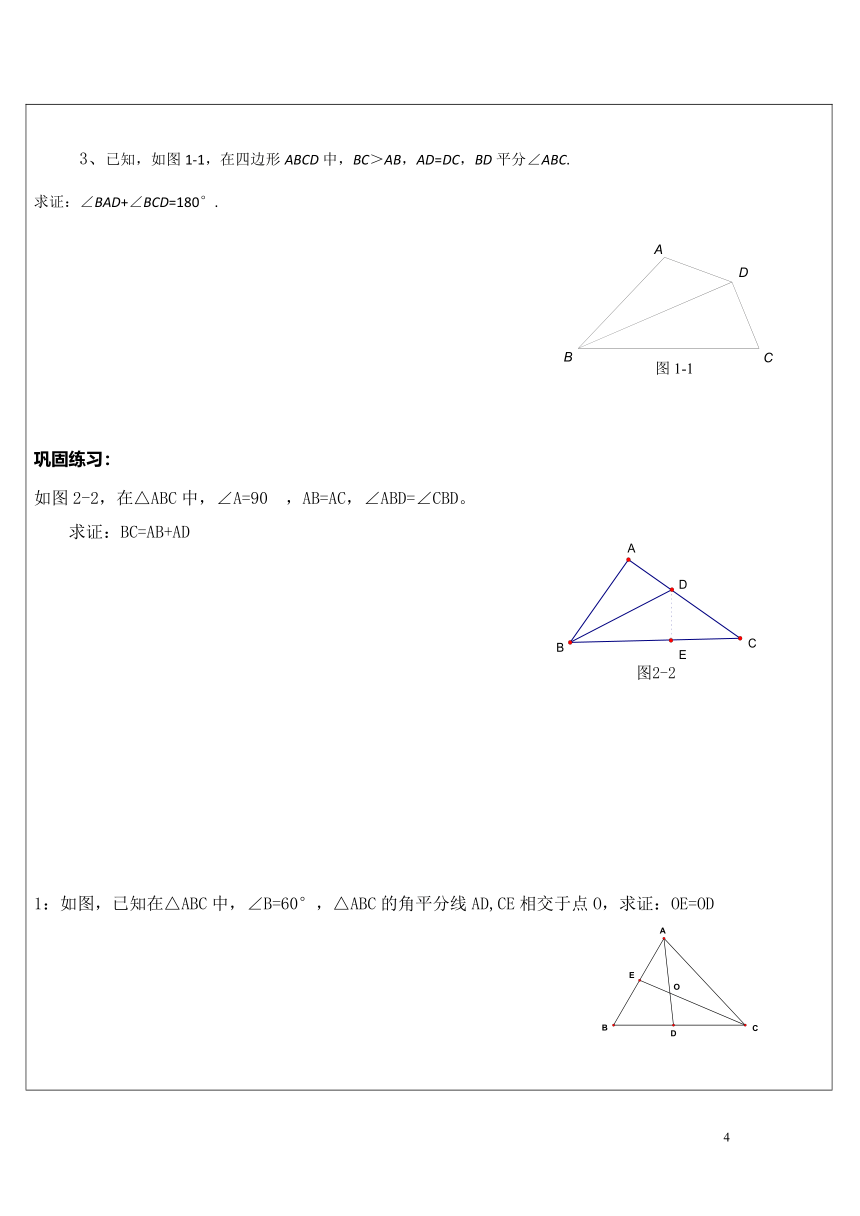
1、已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
2、如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.
3、已知:如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC.
求证:AE平分
4、已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE
5、已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
知识点二、角平分线构造全等法
即利用角平分线构造全等三角形法。遇到角平分线有三种添辅助线的方法,(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。(3)可以在该角的两边上,距离角的顶点相等长度的位置上截取二点,然后从这两点再向角平分线上的某点作边线,构造一对全等三角形。
(一)角分线上点向角两边作垂线构全等
可以自角平分线上的某一点向角的两边作垂线,形成一对全等三角形。所考知识点常常是角平分线的性质定理或逆定理.
3、已知,如图1-1,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC.
求证:∠BAD+∠BCD=180°.
巩固练习:
如图2-2,在△ABC中,∠A=90?,AB=AC,∠ABD=∠CBD。
求证:BC=AB+AD
1:如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O,求证:OE=OD
2:如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;(2)如果AB=,AC=,求AE、BE的长.
已知:如图1-3,AB=2AC,∠BAD=∠CAD,DA=DB,求证DC⊥AC
。
已知:如图1-4,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB-AC=CD
(二):作角平分线的垂线构等腰三角形
从角的一边上的一点作角平分线的垂线,使之与角的两边相交,则截得一个等腰三角形,垂足为底边上的中点,该角平分线又成为底边上的中线和高,以利用中位线的性质与等腰三角形的三线合一的性质。(如果题目中有垂直于角平分线的线段,则延长该线段与角的另一边相交)。
4、如图3-2,AB=AC,∠BAC=90?,AD为∠ABC的平分线,CE⊥BE.求证:BD=2CE。
(三)、以角分线上一点做角的另一边的平行线
有角平分线时,常过角平分线上的一点作角的一边的平行线,从而构造等腰三角形。或通过一边上的点作角平分线的平行线与另外一边的反向延长线相交,从而也构造等腰三角形。如图4-1和图4-2所示。
1、如图,BC>BA,BD平分∠ABC,且AD=CD,求证:∠A+∠C=180。
如图,AB∥CD,AE、DE分别平分∠BAD各∠ADE,求证:AD=AB+CD。
知识点三、截长法与补短法:
具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.
(一)截长
在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;
5、已知:如图,△ABC中,AD平分∠BAC,若∠C=2∠B,证明:AB=AC+CD.
2.已知:如图,△ABC中,∠A=60°,∠B与∠C的平分线BE,CF交于点I,求证:BC=BF+CE.
(二)补短
将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段
6、已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,求证:BE=CF+AE.
巩固练习
1.已知:如图,在△ABC中,AB=AC,D为△ABC外一点,∠ABD=60°,AB=BD+DC,求证:∠ACD=60°.
2.已知:如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,求证:BC+DC=AC.
知识点四、旋转
1:正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
利用特殊图形可通过旋转变换构造全等三角形
1、设点P为等边三角形ABC内任一点,试比较线段PA与PB+PC的大小.
简析 由于△ABC是等边三角形,所以可以将△ABP绕点A旋转60°到△ACP′的位置,连结PP′,则△ACP′≌△ABP(SAS),所以AP′=AP,CP′=BP,△APP′是等边三角形,即PP′=PA,在△CPP′中,因为PP′<PC+P′C,所以PA<PB+PC.
说明 由于图形旋转的前后,只是位置发生了变化,而形状和大小都没有改变,所以对于等边三角形、正方形等特殊的图形我们可以利用旋转的方法构造全等三角形来解题.
利用高可以高线为对称轴构造全等三角形
2、在△ABC中,AD⊥BC,若∠C=2∠B.试比较线段BD与AC+CD的大小.
简析 由于AD⊥BC,所以可在BD上截取DE=DC,
于是可得△ADE≌△ADC(SAS),所以AE=AC,∠AED=∠C,
又∠C=2∠B,所以∠AED=2∠B,而∠AED=∠B+∠BAE,
即∠B=∠BAE,所以BE=AE=AC,所以BD=BE+DE=AE+DE=AC+CD.
说明 利用三角形高的性质,在几何解题时,可以高线为对称轴构造全等三角形求解.
利用利用平行线构造全等三角形
3、△ABC中,AB=AC,E是AB上任意一点,延长AC到F,连接EF交BC于M,且EM=FM试说明线段BE与CF相等的理由.
简析 由于BE与CF的位置较散,故可考虑将线段CF平移到ED,所以过点E作
ED∥CF,则∠EDB=∠ACB,∠EDM=∠FCM,由于EM=FM,∠EMD=∠FMC,所以△EMD≌△FMC(AAS),所以ED=CF,又因为AB=AC,所以∠B=∠ACB,即∠B=∠EDB,所以EB=ED,所以BE=CF.
说明 这里通过辅助线将较散的结论相对集中,使求解的难度降低.
例3:已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
提示:倍长AD至G,连接BG,证明ΔBDG≌ΔCDA
三角形BEG是等腰三角形
总结口诀:图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
10
八年级
教学内容
构造全等法
【知识归纳】
知识点一、倍长中线法:
遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”
法构造全等三角形.即把中线延长一倍,来构造全等三角形。
△ABC中
方式1:
延长AD到E,
AD是BC边中线
使DE=AD,
连接BE
方式2:间接倍长
作CF⊥AD于F,
延长MD到N,
作BE⊥AD的延长线于E
使DN=MD,
连接BE
连接CD
1、已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________.
2、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
巩固练习:
1、已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
2、如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.
3、已知:如图,在中,,D、E在BC上,且DE=EC,过D作交AE于点F,DF=AC.
求证:AE平分
4、已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE
5、已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
知识点二、角平分线构造全等法
即利用角平分线构造全等三角形法。遇到角平分线有三种添辅助线的方法,(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。(3)可以在该角的两边上,距离角的顶点相等长度的位置上截取二点,然后从这两点再向角平分线上的某点作边线,构造一对全等三角形。
(一)角分线上点向角两边作垂线构全等
可以自角平分线上的某一点向角的两边作垂线,形成一对全等三角形。所考知识点常常是角平分线的性质定理或逆定理.
3、已知,如图1-1,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC.
求证:∠BAD+∠BCD=180°.
巩固练习:
如图2-2,在△ABC中,∠A=90?,AB=AC,∠ABD=∠CBD。
求证:BC=AB+AD
1:如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD,CE相交于点O,求证:OE=OD
2:如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)说明BE=CF的理由;(2)如果AB=,AC=,求AE、BE的长.
已知:如图1-3,AB=2AC,∠BAD=∠CAD,DA=DB,求证DC⊥AC
。
已知:如图1-4,在△ABC中,∠C=2∠B,AD平分∠BAC,求证:AB-AC=CD
(二):作角平分线的垂线构等腰三角形
从角的一边上的一点作角平分线的垂线,使之与角的两边相交,则截得一个等腰三角形,垂足为底边上的中点,该角平分线又成为底边上的中线和高,以利用中位线的性质与等腰三角形的三线合一的性质。(如果题目中有垂直于角平分线的线段,则延长该线段与角的另一边相交)。
4、如图3-2,AB=AC,∠BAC=90?,AD为∠ABC的平分线,CE⊥BE.求证:BD=2CE。
(三)、以角分线上一点做角的另一边的平行线
有角平分线时,常过角平分线上的一点作角的一边的平行线,从而构造等腰三角形。或通过一边上的点作角平分线的平行线与另外一边的反向延长线相交,从而也构造等腰三角形。如图4-1和图4-2所示。
1、如图,BC>BA,BD平分∠ABC,且AD=CD,求证:∠A+∠C=180。
如图,AB∥CD,AE、DE分别平分∠BAD各∠ADE,求证:AD=AB+CD。
知识点三、截长法与补短法:
具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.
(一)截长
在长线段中截取一段等于另两条中的一条,然后证明剩下部分等于另一条;
5、已知:如图,△ABC中,AD平分∠BAC,若∠C=2∠B,证明:AB=AC+CD.
2.已知:如图,△ABC中,∠A=60°,∠B与∠C的平分线BE,CF交于点I,求证:BC=BF+CE.
(二)补短
将一条短线段延长,延长部分等于另一条短线段,然后证明新线段等于长线段
6、已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,求证:BE=CF+AE.
巩固练习
1.已知:如图,在△ABC中,AB=AC,D为△ABC外一点,∠ABD=60°,AB=BD+DC,求证:∠ACD=60°.
2.已知:如图,四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,求证:BC+DC=AC.
知识点四、旋转
1:正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
利用特殊图形可通过旋转变换构造全等三角形
1、设点P为等边三角形ABC内任一点,试比较线段PA与PB+PC的大小.
简析 由于△ABC是等边三角形,所以可以将△ABP绕点A旋转60°到△ACP′的位置,连结PP′,则△ACP′≌△ABP(SAS),所以AP′=AP,CP′=BP,△APP′是等边三角形,即PP′=PA,在△CPP′中,因为PP′<PC+P′C,所以PA<PB+PC.
说明 由于图形旋转的前后,只是位置发生了变化,而形状和大小都没有改变,所以对于等边三角形、正方形等特殊的图形我们可以利用旋转的方法构造全等三角形来解题.
利用高可以高线为对称轴构造全等三角形
2、在△ABC中,AD⊥BC,若∠C=2∠B.试比较线段BD与AC+CD的大小.
简析 由于AD⊥BC,所以可在BD上截取DE=DC,
于是可得△ADE≌△ADC(SAS),所以AE=AC,∠AED=∠C,
又∠C=2∠B,所以∠AED=2∠B,而∠AED=∠B+∠BAE,
即∠B=∠BAE,所以BE=AE=AC,所以BD=BE+DE=AE+DE=AC+CD.
说明 利用三角形高的性质,在几何解题时,可以高线为对称轴构造全等三角形求解.
利用利用平行线构造全等三角形
3、△ABC中,AB=AC,E是AB上任意一点,延长AC到F,连接EF交BC于M,且EM=FM试说明线段BE与CF相等的理由.
简析 由于BE与CF的位置较散,故可考虑将线段CF平移到ED,所以过点E作
ED∥CF,则∠EDB=∠ACB,∠EDM=∠FCM,由于EM=FM,∠EMD=∠FMC,所以△EMD≌△FMC(AAS),所以ED=CF,又因为AB=AC,所以∠B=∠ACB,即∠B=∠EDB,所以EB=ED,所以BE=CF.
说明 这里通过辅助线将较散的结论相对集中,使求解的难度降低.
例3:已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF
提示:倍长AD至G,连接BG,证明ΔBDG≌ΔCDA
三角形BEG是等腰三角形
总结口诀:图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
10
