青岛(六三)版数学三上 5.2两位数除以一位数的笔算及验算 教案
文档属性
| 名称 | 青岛(六三)版数学三上 5.2两位数除以一位数的笔算及验算 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 714.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 20:42:07 | ||
图片预览




文档简介
教学设计
课 题 两位数除以一位数的笔算和验算 教案序号
教 学
目
标 知识
目标 在分小棒的操作过程中,理解两位数除以一位数的笔算除法中“从被除数的高位开始算”、“除到哪一位就把商写到那一位上面”和“十位上有余数要和个位合起来再除”的道理,在理解算理的过程中逐步掌握算法,并能正确进行计算。
能力
目标 在探索算理和算法的过程中,经历从动手操作→直观表象→符号化抽象的“数学化”的过程。
情感
目标 体会数学与生活的联系,体验运用数学知识解决实际问题的工具性,提高学习数学的兴趣。
教学重点 理解算理掌握算法掌握笔算除法的步骤和商的书写位置。
教学难点 让学生理解每求出一位商后,如果有余数就要把余数与被除数的下一位合起来继续除的道理,理解除法竖式的分层书写形式的必要性
课时安排
教学准备 学具木棒、教具木棒,课件、练习纸
教
学
设
计
教
学
设
计
主 备 内 容 二次备课
一、创设情境,引出问题
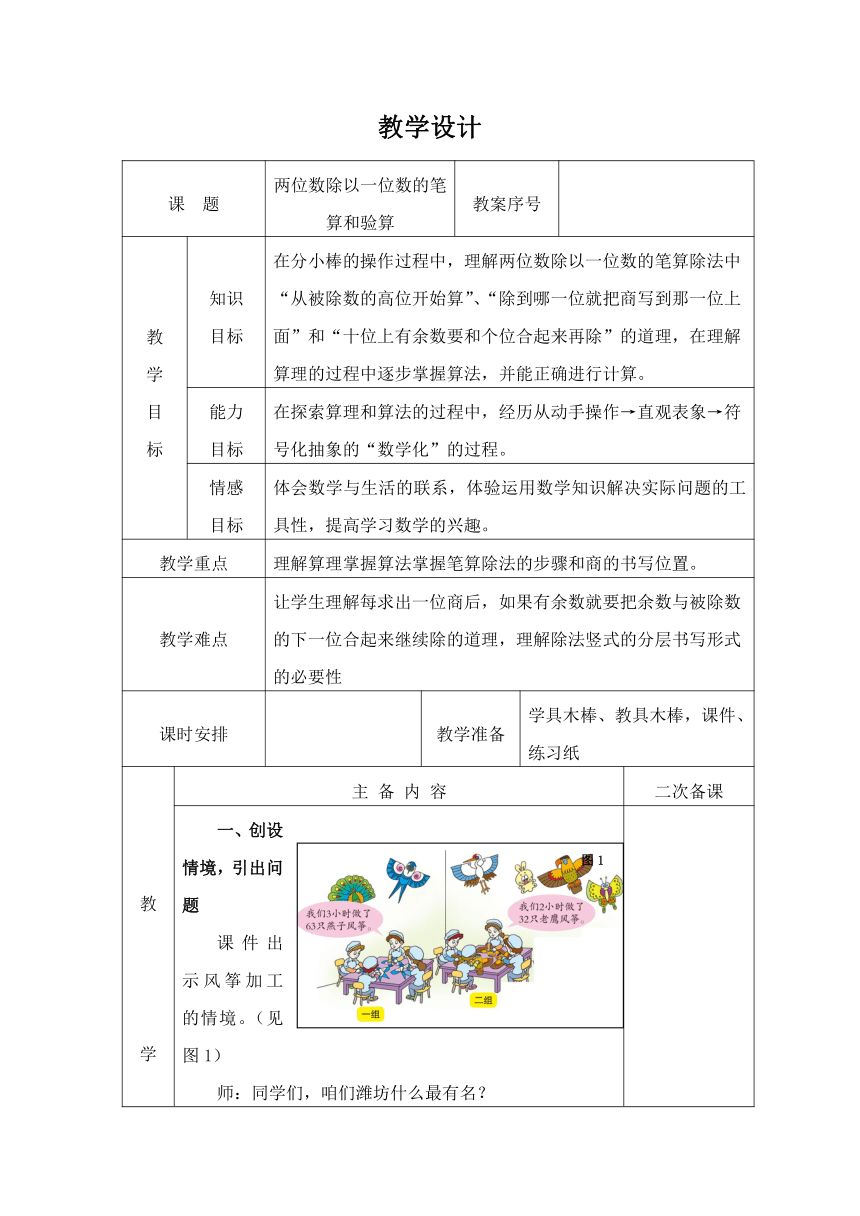
课件出示风筝加工的情境。(见图1)
师:同学们,咱们潍坊什么最有名?
生:风筝。
师:对,潍坊市风筝的发源地,潍坊风筝历史悠久、做工精湛,是国家非物质文化遗产之一。今天,老师带领大家一块去参观风筝加工厂,去探索一下其中的数学奥秘。
这是风筝加工厂的工人正在加工风筝的场景。在图中你发现了哪些数学信息?
预设1:一组3小时做了63只燕子风筝。
预设2:二组2小时做了32只老鹰风筝。
师:能不能提出一个可以用除法解决的问题?
预设1:一组平均每小时做了多少只燕子风筝?
预设2:二组平均每小时做了多少只老鹰风筝?
师:怎么列式?
预设63÷3 32÷2
(板书算式)
师:为什么用除法列式?
生:一组3小时做了63只燕子风筝,要求一组平均每小时做了多少只燕子风筝,就是讲63平均分成3分,取其中的一份,所以用63÷3。
师:讲解的很清楚。
师:看看这两个算式被除数和除数有什么特点?
生:被除数是两位数,除数是一位数
师:观察的真仔细,这就是今天咱们要学的两位数除以一位数。(板书课题)
师:老师本来打算要带63只风筝来,让大家分分看,可是太不方便了……
预设:可以用学具代替。
师:想法真不错,分大的东西不方便,我们可以用小的模型来代替。
(一)动手操作分小棒
师:现在请每位同学拿出6捆小棒,每捆是10根,再拿出3根。把这63根小棒平均分成3份,分分看。
(学生独立分小棒,师巡视指导)
师:谁能到前面来分给大家看一看?
预设:(先边6捆,再分3根)
师:谁看清楚了?他是怎么分的?
预设1:他先分的成捆的,又分了成根的。
预设2:他先分了6捆,又分了3根。
预设3:他先把6捆平均分成3份,每份分得2捆;又把3根平均分成3份,每份分得1根。
师:说得真清楚。请你也像他一样说一说刚才分小棒的过程。
(生自由说分小棒的操作过程)
(二)课件演示分小棒
(老师播放课件,边演示边说分小棒的过程)
师:先把6捆小棒平均分成3份,每份分得2捆;再把3根小棒平均分成3份,每份分得1根。合起来每份是21根。
(三)用竖式表示分小棒的过程
师:数学最大的特点就是用数和符号来表示生活中的一些现象。我们刚才分小棒的过程就可以用除法的竖式来表示。现在就请你试着用除法的竖式把刚才分小棒的过程表示出来。
(生独立尝试用竖式表示分小棒的过程,师巡视选择有代表性的方法准备展示)
(四)展示交流
师:哪个同学到黑板上展示一下你的竖式计算?
我们一起来看一看。先来看第一种表示方法(见右图)。
生边写边说:把63根小棒平均分成3份,每份就分得21根小棒。所以商就是21。
师:对于这种方法你有什么看法?
预设1:这样表示很简单。
预设2:这样表示虽然简单,但是让人看不懂你在分小棒时到底分了几次。
师:是呀,确实很简单,但有点遗憾的是没把我们分小棒时分了两次这个过程表示出来。
师:再来看这位同学的表示方法(见右图)。很特别,请你说说你是怎么想的。
生说:
先把6捆小棒平均分成3份,每一份分得2捆,所以这里就用商2表示,整捆的分完了就用0表示。再把3根小棒平均分成3份,每一份分得1根,就用商1表示,单根的分完了也用0表示。
师:请大家说说对这种方法的感觉。
针对学生的回答教师总结。
师:这个同学的表示方法,和第一种比这个能表示出分两次过程。但大家感觉就是有点不太清楚,看不太懂。
师:那怎样表示既能表示出分两次的过程,又能比较简单,还能让大家看的很清楚呢?请大家看屏幕。
(五)课件演示分小棒和用竖式计算的过程
师:(边演示边介绍)
把63根小棒平均分成3份;我们就用竖式63除以3表示。
先分6捆;竖式中就先用十位上的6除以3。
每份分得2捆;那就要商2。
师:这个2写在哪?为什么?
预设:写在十位上,因为它表示2个十。
师:已经分完了6捆;竖式中就在这里写6。这个6怎么算出来的?
预设:二三得六。
师:用除数3和商2相乘得到的。
师:整捆的分完了,没有余下整捆的;竖式中要算出十位的余数,正好是0,但因为还没有分完所有的小棒,还要继续分,所以这里不写0。
分完了6捆,再分3根;竖式中就要再用个位上的3除以2,为了更清楚的表示这是第二次分的,竖式中一般把个位上的3先落下来。
每份又分得1根;竖式中就再商1。
师:这个1写哪?为什么?
引导学生回答:要写在个位上,它表示的是1个一。
师:又分完了3根;就在这写3。这个3是怎么算出来的?
使学生明确:商1和除数3相乘得来的。
师:所有的小棒都分完了;我们再算出余数,还是0,并且所有小棒都分完了,所以在这里就用0来表示。
(七)板演竖式
师:刚才我们一起将分小棒和列竖式的过程进行了对比,其实竖式就是用数字和符号表示出了分东西的过程。现在我们再一起回顾一下用竖式计算的过程。
(学生板演讲解,老师总结)
先用十位上的6除以3,在商的十位上商2;再用除数3和商2相乘得6;算出十位的余数,相减得0,因为还没有全部算完,这里不写0;再把个位上的3落下来,用个位上的3再除以3,在商的个位上商1;然后用除数3和商1相乘得3;最后算出余数,相减还是得0,到这里全部算完了,要把0写上。
师:请大家把刚才自己写的竖式根据我们一起探索出来的新的书写形式修改一下。
随堂联系:
填一填:竖式计算64÷2 48÷2 84÷2 99÷9
学生独立完成后,找学生全班汇报,并讲解如何进行计算的。
三、理解32÷2的算理,体会算法
师:再来一起回想一下刚才的学习过程。一开始我们通过生活中做风筝的情境,提出了一个用除法解决的问题,列出了一道新的除法算式;我们又用小棒代替风筝自己动手分了小棒,然后又用竖式表示出了分小棒的过程。在这个过程中我们学会了新的用竖式计算除法的方法。
师:刚才我们是把63平均分成了3份。如果要求二组平均每小时做多少只风筝就要把32平均分成2份,又该怎么分呢?
(一)动手操作分小棒
师:请同学们再拿出32根小棒,动手分一分,把32根小棒平均分成2份。
(学生独立分小棒,师巡视指导)
师:有些同学怎么停下来了?遇到什么困难了吗?
预设:整捆的分完之后还剩下了1捆,怎么办呀?
师:谁有好办法?
预设:可以把那1捆拆开再分。
师:好办法!把剩下的1捆拆开和2根单根的合起来再分。
(学生继续分小棒,师巡视指导)
师:谁能到前面来分给大家看一看?
预设:(边分边说)我先把3捆小棒平均分成2份,每份只能分得1捆;然后把剩下的这1捆拆开和这2根合起来就是12根,再平均分成2份,每份又分得6根。
(二)脑中想象分小棒
师:请大家闭上眼睛在脑子里想一想分小棒的过程。
(三)用竖式表示分小棒的过程
师:请你再试着用竖式把刚才分小棒的过程表示出来。
(生独立用竖式表示分小棒的过程,师巡视并请一名学生板演)
(四)展示、交流
师:请你说一说是怎么算的。
预设:先用十位上的3除以2,商1,再用1乘2得2,然后用3减2,余下1,再把2落下来,合起来是12,用12再除以2,商6,二六十二,最后用12减12是0。
师:说得真清楚。我们再一起看一看分小棒和列竖式的过程。
(五)课件演示分小棒和列竖式的过程
师:(边演示边介绍)
把32根小棒平均分成2份;用竖式32除以2表示。
先分3捆;竖式中就先用十位上的3除以2。
每份只能分得1捆;在十位上商1。
已经分完了2捆;竖式中就是1乘2得2。
还剩下1捆;十位上的余数是1。
把这1捆拆开变成10根,和2根合起来是12根,再平均分成2份;竖式中把个位上的2落下来,再用12除以2。
每份又分得6根;再在个位上商6。
又分完了12根;竖式中就是2乘6得12。
所有的小棒都分完了;竖式中再算出余数,是0。
师:刚才用竖式计算时有错误的同学请再修改一下,然后和你的同位互相说一说是怎样算的。
四、巩固练习。
捡贝壳。
竖式计算84÷6 91÷7 58÷2 92÷4
学生独立完成后,找学生全班汇报,并讲解如何进行计算的。
五、总结。
1.谈收获。
师:通过今天我们进一步学习除法,你又有哪些新的收获?
预设:我觉得今天学习的除法很简单。
预设:我觉得学数学很有意思。
教学反思1 运用知识的迁移,让学生自主探索新知。数学教学一定要充分考虑学生已有的知识基础,学生通过自己的独立思考就能获取的知识教师完全可以放心、放手让学生自己去实现知识的迁移。
教学反思2 出现错误是学生学习过程当中必然要经历的过程,在课堂中引导学生思考:计算过程错在哪里?为什么会出现这样的错误?正确的运算是什么?在教学过程中,我给学生提供了充分的时间和空间,引导学生分析、比较。
课 题 两位数除以一位数的笔算和验算 教案序号
教 学
目
标 知识
目标 在分小棒的操作过程中,理解两位数除以一位数的笔算除法中“从被除数的高位开始算”、“除到哪一位就把商写到那一位上面”和“十位上有余数要和个位合起来再除”的道理,在理解算理的过程中逐步掌握算法,并能正确进行计算。
能力
目标 在探索算理和算法的过程中,经历从动手操作→直观表象→符号化抽象的“数学化”的过程。
情感
目标 体会数学与生活的联系,体验运用数学知识解决实际问题的工具性,提高学习数学的兴趣。
教学重点 理解算理掌握算法掌握笔算除法的步骤和商的书写位置。
教学难点 让学生理解每求出一位商后,如果有余数就要把余数与被除数的下一位合起来继续除的道理,理解除法竖式的分层书写形式的必要性
课时安排
教学准备 学具木棒、教具木棒,课件、练习纸
教
学
设
计
教
学
设
计
主 备 内 容 二次备课
一、创设情境,引出问题
课件出示风筝加工的情境。(见图1)
师:同学们,咱们潍坊什么最有名?
生:风筝。
师:对,潍坊市风筝的发源地,潍坊风筝历史悠久、做工精湛,是国家非物质文化遗产之一。今天,老师带领大家一块去参观风筝加工厂,去探索一下其中的数学奥秘。
这是风筝加工厂的工人正在加工风筝的场景。在图中你发现了哪些数学信息?
预设1:一组3小时做了63只燕子风筝。
预设2:二组2小时做了32只老鹰风筝。
师:能不能提出一个可以用除法解决的问题?
预设1:一组平均每小时做了多少只燕子风筝?
预设2:二组平均每小时做了多少只老鹰风筝?
师:怎么列式?
预设63÷3 32÷2
(板书算式)
师:为什么用除法列式?
生:一组3小时做了63只燕子风筝,要求一组平均每小时做了多少只燕子风筝,就是讲63平均分成3分,取其中的一份,所以用63÷3。
师:讲解的很清楚。
师:看看这两个算式被除数和除数有什么特点?
生:被除数是两位数,除数是一位数
师:观察的真仔细,这就是今天咱们要学的两位数除以一位数。(板书课题)
师:老师本来打算要带63只风筝来,让大家分分看,可是太不方便了……
预设:可以用学具代替。
师:想法真不错,分大的东西不方便,我们可以用小的模型来代替。
(一)动手操作分小棒
师:现在请每位同学拿出6捆小棒,每捆是10根,再拿出3根。把这63根小棒平均分成3份,分分看。
(学生独立分小棒,师巡视指导)
师:谁能到前面来分给大家看一看?
预设:(先边6捆,再分3根)
师:谁看清楚了?他是怎么分的?
预设1:他先分的成捆的,又分了成根的。
预设2:他先分了6捆,又分了3根。
预设3:他先把6捆平均分成3份,每份分得2捆;又把3根平均分成3份,每份分得1根。
师:说得真清楚。请你也像他一样说一说刚才分小棒的过程。
(生自由说分小棒的操作过程)
(二)课件演示分小棒
(老师播放课件,边演示边说分小棒的过程)
师:先把6捆小棒平均分成3份,每份分得2捆;再把3根小棒平均分成3份,每份分得1根。合起来每份是21根。
(三)用竖式表示分小棒的过程
师:数学最大的特点就是用数和符号来表示生活中的一些现象。我们刚才分小棒的过程就可以用除法的竖式来表示。现在就请你试着用除法的竖式把刚才分小棒的过程表示出来。
(生独立尝试用竖式表示分小棒的过程,师巡视选择有代表性的方法准备展示)
(四)展示交流
师:哪个同学到黑板上展示一下你的竖式计算?
我们一起来看一看。先来看第一种表示方法(见右图)。
生边写边说:把63根小棒平均分成3份,每份就分得21根小棒。所以商就是21。
师:对于这种方法你有什么看法?
预设1:这样表示很简单。
预设2:这样表示虽然简单,但是让人看不懂你在分小棒时到底分了几次。
师:是呀,确实很简单,但有点遗憾的是没把我们分小棒时分了两次这个过程表示出来。
师:再来看这位同学的表示方法(见右图)。很特别,请你说说你是怎么想的。
生说:
先把6捆小棒平均分成3份,每一份分得2捆,所以这里就用商2表示,整捆的分完了就用0表示。再把3根小棒平均分成3份,每一份分得1根,就用商1表示,单根的分完了也用0表示。
师:请大家说说对这种方法的感觉。
针对学生的回答教师总结。
师:这个同学的表示方法,和第一种比这个能表示出分两次过程。但大家感觉就是有点不太清楚,看不太懂。
师:那怎样表示既能表示出分两次的过程,又能比较简单,还能让大家看的很清楚呢?请大家看屏幕。
(五)课件演示分小棒和用竖式计算的过程
师:(边演示边介绍)
把63根小棒平均分成3份;我们就用竖式63除以3表示。
先分6捆;竖式中就先用十位上的6除以3。
每份分得2捆;那就要商2。
师:这个2写在哪?为什么?
预设:写在十位上,因为它表示2个十。
师:已经分完了6捆;竖式中就在这里写6。这个6怎么算出来的?
预设:二三得六。
师:用除数3和商2相乘得到的。
师:整捆的分完了,没有余下整捆的;竖式中要算出十位的余数,正好是0,但因为还没有分完所有的小棒,还要继续分,所以这里不写0。
分完了6捆,再分3根;竖式中就要再用个位上的3除以2,为了更清楚的表示这是第二次分的,竖式中一般把个位上的3先落下来。
每份又分得1根;竖式中就再商1。
师:这个1写哪?为什么?
引导学生回答:要写在个位上,它表示的是1个一。
师:又分完了3根;就在这写3。这个3是怎么算出来的?
使学生明确:商1和除数3相乘得来的。
师:所有的小棒都分完了;我们再算出余数,还是0,并且所有小棒都分完了,所以在这里就用0来表示。
(七)板演竖式
师:刚才我们一起将分小棒和列竖式的过程进行了对比,其实竖式就是用数字和符号表示出了分东西的过程。现在我们再一起回顾一下用竖式计算的过程。
(学生板演讲解,老师总结)
先用十位上的6除以3,在商的十位上商2;再用除数3和商2相乘得6;算出十位的余数,相减得0,因为还没有全部算完,这里不写0;再把个位上的3落下来,用个位上的3再除以3,在商的个位上商1;然后用除数3和商1相乘得3;最后算出余数,相减还是得0,到这里全部算完了,要把0写上。
师:请大家把刚才自己写的竖式根据我们一起探索出来的新的书写形式修改一下。
随堂联系:
填一填:竖式计算64÷2 48÷2 84÷2 99÷9
学生独立完成后,找学生全班汇报,并讲解如何进行计算的。
三、理解32÷2的算理,体会算法
师:再来一起回想一下刚才的学习过程。一开始我们通过生活中做风筝的情境,提出了一个用除法解决的问题,列出了一道新的除法算式;我们又用小棒代替风筝自己动手分了小棒,然后又用竖式表示出了分小棒的过程。在这个过程中我们学会了新的用竖式计算除法的方法。
师:刚才我们是把63平均分成了3份。如果要求二组平均每小时做多少只风筝就要把32平均分成2份,又该怎么分呢?
(一)动手操作分小棒
师:请同学们再拿出32根小棒,动手分一分,把32根小棒平均分成2份。
(学生独立分小棒,师巡视指导)
师:有些同学怎么停下来了?遇到什么困难了吗?
预设:整捆的分完之后还剩下了1捆,怎么办呀?
师:谁有好办法?
预设:可以把那1捆拆开再分。
师:好办法!把剩下的1捆拆开和2根单根的合起来再分。
(学生继续分小棒,师巡视指导)
师:谁能到前面来分给大家看一看?
预设:(边分边说)我先把3捆小棒平均分成2份,每份只能分得1捆;然后把剩下的这1捆拆开和这2根合起来就是12根,再平均分成2份,每份又分得6根。
(二)脑中想象分小棒
师:请大家闭上眼睛在脑子里想一想分小棒的过程。
(三)用竖式表示分小棒的过程
师:请你再试着用竖式把刚才分小棒的过程表示出来。
(生独立用竖式表示分小棒的过程,师巡视并请一名学生板演)
(四)展示、交流
师:请你说一说是怎么算的。
预设:先用十位上的3除以2,商1,再用1乘2得2,然后用3减2,余下1,再把2落下来,合起来是12,用12再除以2,商6,二六十二,最后用12减12是0。
师:说得真清楚。我们再一起看一看分小棒和列竖式的过程。
(五)课件演示分小棒和列竖式的过程
师:(边演示边介绍)
把32根小棒平均分成2份;用竖式32除以2表示。
先分3捆;竖式中就先用十位上的3除以2。
每份只能分得1捆;在十位上商1。
已经分完了2捆;竖式中就是1乘2得2。
还剩下1捆;十位上的余数是1。
把这1捆拆开变成10根,和2根合起来是12根,再平均分成2份;竖式中把个位上的2落下来,再用12除以2。
每份又分得6根;再在个位上商6。
又分完了12根;竖式中就是2乘6得12。
所有的小棒都分完了;竖式中再算出余数,是0。
师:刚才用竖式计算时有错误的同学请再修改一下,然后和你的同位互相说一说是怎样算的。
四、巩固练习。
捡贝壳。
竖式计算84÷6 91÷7 58÷2 92÷4
学生独立完成后,找学生全班汇报,并讲解如何进行计算的。
五、总结。
1.谈收获。
师:通过今天我们进一步学习除法,你又有哪些新的收获?
预设:我觉得今天学习的除法很简单。
预设:我觉得学数学很有意思。
教学反思1 运用知识的迁移,让学生自主探索新知。数学教学一定要充分考虑学生已有的知识基础,学生通过自己的独立思考就能获取的知识教师完全可以放心、放手让学生自己去实现知识的迁移。
教学反思2 出现错误是学生学习过程当中必然要经历的过程,在课堂中引导学生思考:计算过程错在哪里?为什么会出现这样的错误?正确的运算是什么?在教学过程中,我给学生提供了充分的时间和空间,引导学生分析、比较。
