人教版九年级下册28.1 锐角三角函数 测量类应用题(讲义 含简单答案)
文档属性
| 名称 | 人教版九年级下册28.1 锐角三角函数 测量类应用题(讲义 含简单答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览


文档简介
测量类应用题(讲义)
??课前预习
一、填写下面学过的知识
1.?_______.
2.?在进行测量时,
从下往上看,视线与水平线的夹角叫做_______;
从上往下看,视线与水平线的夹角叫做_______.
?
3.?利用三角函数求解时,往往需要构造直角三角形,把已知角度信息放到直角三角形中求解,常见图形如下:图3
??知识点睛
1.?正切常用来描述山坡的坡度.坡度也叫_________,指的是坡面的___________与____________的比.
2.?测量类应用题常见类型有:测量物体的高度、船是否会触礁,侧重于___________和_____________.
①解直角三角形,需要在________和________集中处,寻找或构造_________,利用三角函数,表达线段长、建等式;
②结果判断指的是根据题意确定符合要求的标准或范围,计算结果与标准对比来确定符合题意的结果.
??精讲精练
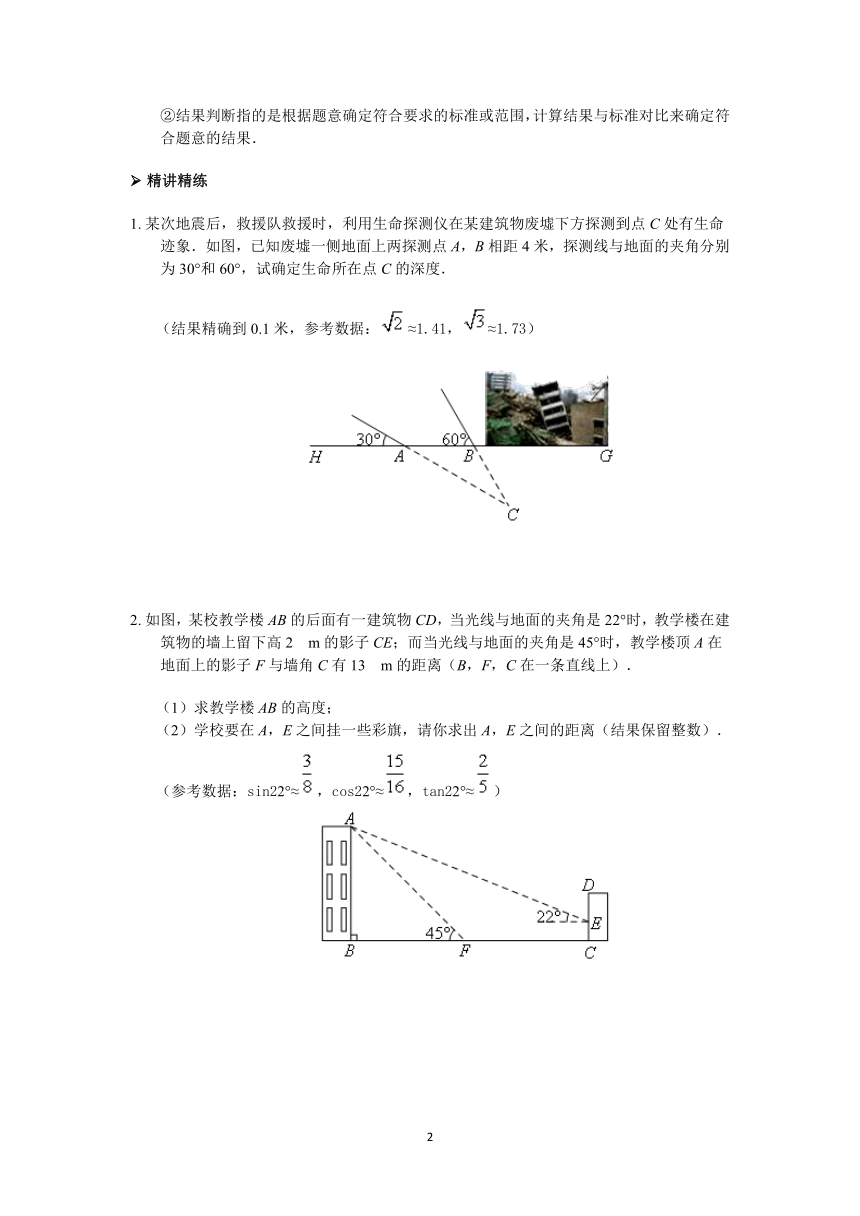
1.?某次地震后,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象.如图,已知废墟一侧地面上两探测点A,B相距4米,探测线与地面的夹角分别为30°和60°,试确定生命所在点C的深度.
(结果精确到0.1米,参考数据:≈1.41,≈1.73)
?
?
2.?如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2?m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13?m的距离(B,F,C在一条直线上).
(1)求教学楼AB的高度;
(2)学校要在A,E之间挂一些彩旗,请你求出A,E之间的距离(结果保留整数).
(参考数据:sin22°≈,cos22°≈,tan22°≈)
?
?
?
?
?
?
?
?
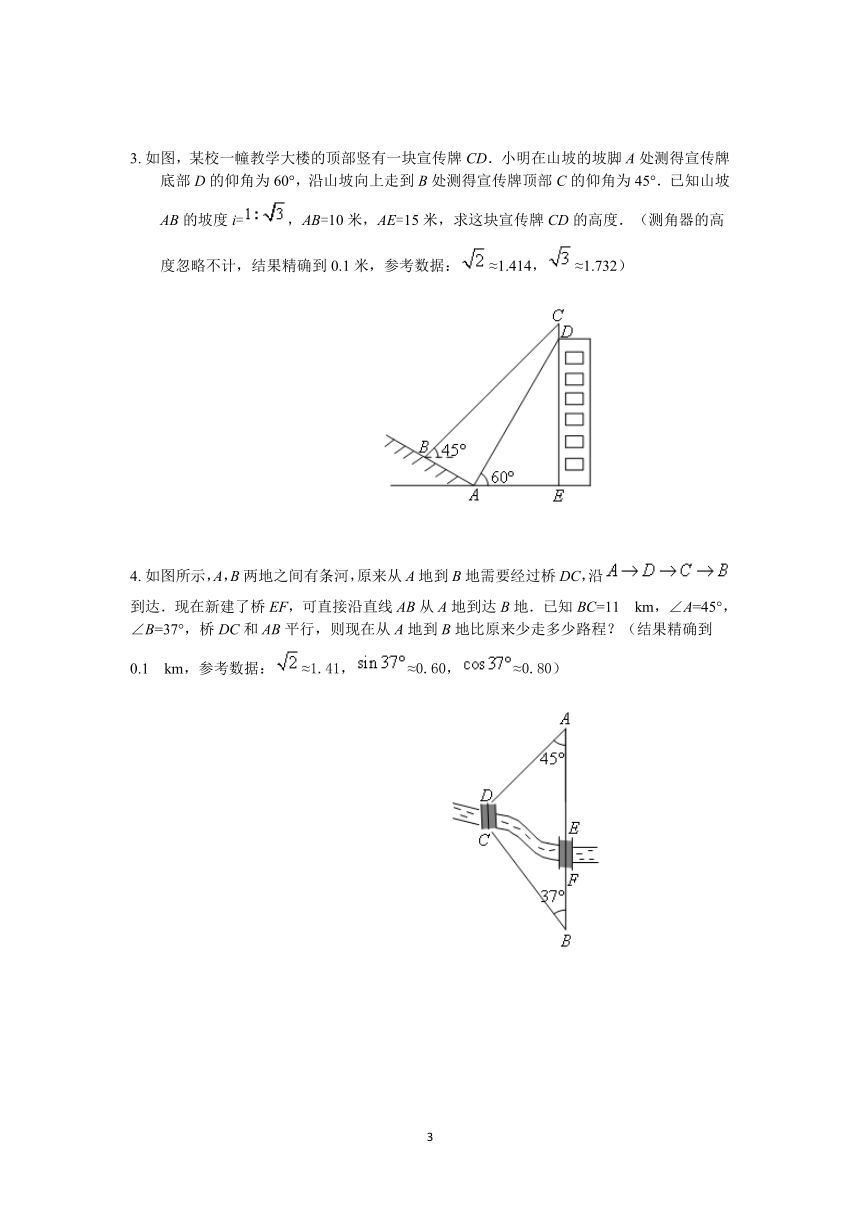
3.?如图,某校一幢教学大楼的顶部竖有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.414,≈1.732)
?
?
4.?如图所示,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿到达.现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11?km,∠A=45°,∠B=37°,桥DC和AB平行,则现在从A地到B地比原来少走多少路程?(结果精确到0.1?km,参考数据:≈1.41,≈0.60,≈0.80)
?
?
?
?
?
?
?
?
5.?如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.
(说明:两问的计算结果均精确到0.1米,参考数据:≈1.41,
≈1.73,≈2.24,≈2.45)
(1)求新传送带AC的长度;
(2)若需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.
?
?
?
?
?6.?如图所示,山坡上有一棵与地面垂直的大树AB,一场大风过后,大树被刮倾斜后从点C处折断倒在山坡上,树的顶部D恰好接触到坡面AE上.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角
∠ADC=60°,AD=4?m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度.(结果精确到个位,参考数据:
≈1.4,≈1.7,≈2.4)
?
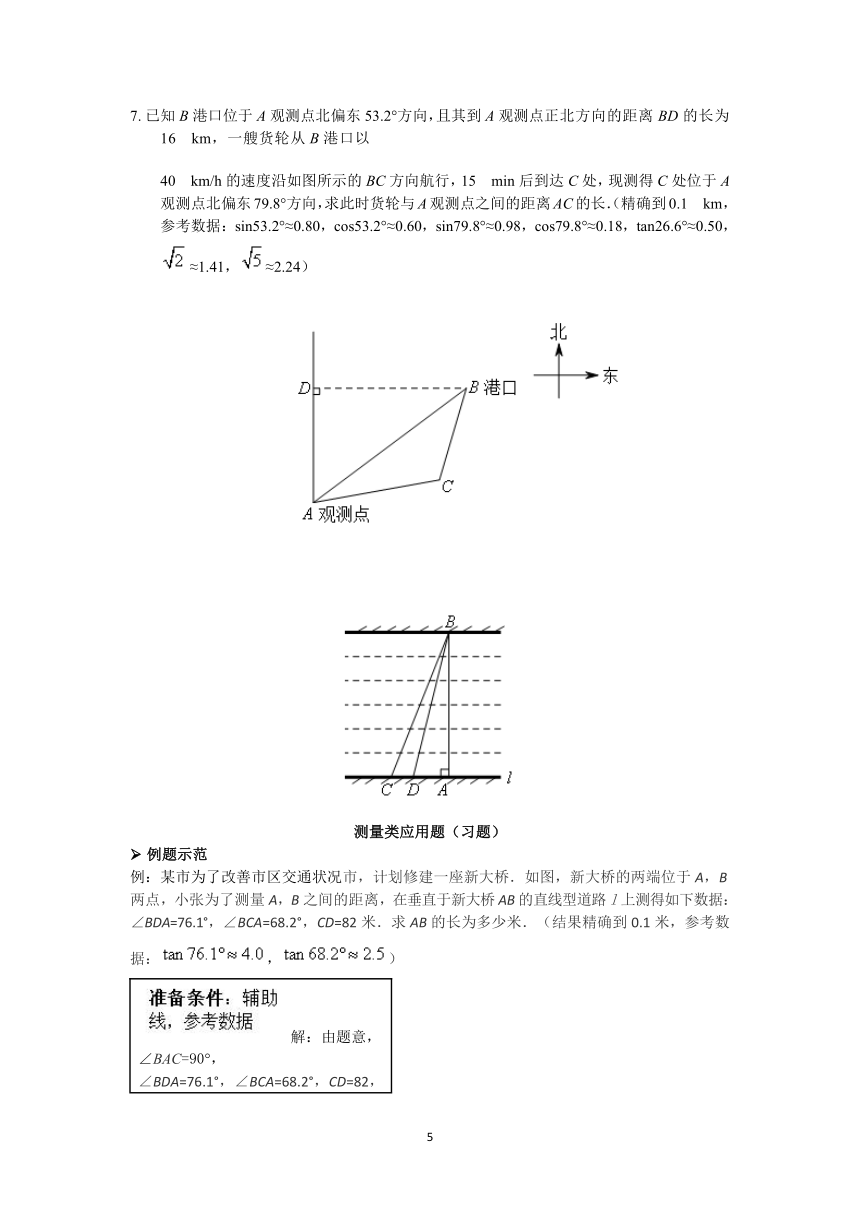
7.?已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16?km,一艘货轮从B港口以
40?km/h的速度沿如图所示的BC方向航行,15?min后到达C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长.(精确到0.1?km,参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,≈1.41,≈2.24)
?
?
?
?
测量类应用题(习题)
??例题示范
例:某市为了改善市区交通状况市,计划修建一座新大桥.如图,新大桥的两端位于A,B两点,小张为了测量A,B之间的距离,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长为多少米.(结果精确到0.1米,参考数据:,)
解:由题意,∠BAC=90°,∠BDA=76.1°,∠BCA=68.2°,CD=82,设AD=a米,则AC=(a+82)米
在Rt△BAD中,∠BDA=76.1°,AD=a∴AB=4a
在Rt△BAC中,∠BCA=68.2°,AC=a+82,∴AB=2.5(a+82)∴4a=2.5(a+82).
∴米即AB的长约为546.7米.
??
??巩固练习
1.?如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C位于北偏西30°的方向上,轮船继续航行2小时后到达B处,在B处测得灯塔C位于北偏西60°的方向上.当轮船到达灯塔C的正东方向上的D处时,求轮船与灯塔C的距离.(结果保留根号)
?
?
?
2.?如图,在某飞机场东西方向的地面l上有一长为1?km的飞机跑道MN,在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
?
?
?
?
?
3.?如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=30米,某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了50米达到B处,测得∠CBN=60°,求河流的宽度CE.
?
?
?
4.?如图,为了测量某山AB的高度,小明先在山脚C点测得山顶A的仰角为45°,然后沿坡度为的斜坡走100米到达D点,在D点测得山顶A的仰角为30°,求山AB的高度.(结果精确到0.1米,参考数据:≈1.73)
?
?
?
?
?
?
?
??
5.?小亮和课外兴趣小组的伙伴们在课外活动中观察大吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米,当吊臂顶端由A′点降落至A点(吊臂长度不变)时,所吊装的重物(大小忽略不计)从B′处恰好放到地面上的B处,紧绷着的吊缆AB=A′B′,AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=20米,且cosA,.
(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B′C.(结果保留根号)
?
?
?
?
?
?
?
?
?
?
?
??思考小结
1.?我们已经学习过方程与不等式应用题,一次函数应用题以及测量类应用题,应用题的处理流程为:
①?理解题意,梳理信息
②?建立模型
③?求解验证,回归实际
2.?我们已经学习过相似,也学习过了三角函数,现在来思考一下它们的联系.
在学习相似三角形判定时知道“两边对应成比例且夹角相等的两个三角形相似”,
即当∠B=∠E,时,△ABC∽△DEF
?
特别地,当∠B=∠E=90°时,若,则△ABC∽△DEF
?
根据比例的性质我们知道可以改写成,而,我们得到
当∠B=∠E=90°时,若,则△ABC∽△DEF,
∠C=∠F.
借助上面的分析,请在下图中进行证明:若,则∠C=∠F.(描述辅助线,给出证明过程)
?
?
【参考答案】
??课前预习
1.?3
2.?仰角;俯角.
??知识点睛
1.?坡比,铅直高度,水平宽度.
2.?解直角三角形,结果判断.①线段,角度,直角三角形.
??精讲精练
1.?3.5米
2.?(1)教学楼AB的高度为12
m;(2)A,E之间的距离为27
m.
3.?这块宣传牌CD的高度为2.7米.
4.?比原来少走4.9
km.
5.?(1)新传送带AC的长度为5.6米;(2)需要挪走,理由略.
6.?(1)75°;(2)这棵大树折断前的高度为10?m.
7.?货轮与A观测点之间的距离AC的长为13.4
km.
【参考答案】
??巩固练习
1.?海里
2.?(1)千米/小时
(2)能,理由略
3.?米
4.?236.5米
5.?(1)6米?(2)()米
??思考小结
2.?证明略
??课前预习
一、填写下面学过的知识
1.?_______.
2.?在进行测量时,
从下往上看,视线与水平线的夹角叫做_______;
从上往下看,视线与水平线的夹角叫做_______.
?
3.?利用三角函数求解时,往往需要构造直角三角形,把已知角度信息放到直角三角形中求解,常见图形如下:图3
??知识点睛
1.?正切常用来描述山坡的坡度.坡度也叫_________,指的是坡面的___________与____________的比.
2.?测量类应用题常见类型有:测量物体的高度、船是否会触礁,侧重于___________和_____________.
①解直角三角形,需要在________和________集中处,寻找或构造_________,利用三角函数,表达线段长、建等式;
②结果判断指的是根据题意确定符合要求的标准或范围,计算结果与标准对比来确定符合题意的结果.
??精讲精练
1.?某次地震后,救援队救援时,利用生命探测仪在某建筑物废墟下方探测到点C处有生命迹象.如图,已知废墟一侧地面上两探测点A,B相距4米,探测线与地面的夹角分别为30°和60°,试确定生命所在点C的深度.
(结果精确到0.1米,参考数据:≈1.41,≈1.73)
?
?
2.?如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2?m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13?m的距离(B,F,C在一条直线上).
(1)求教学楼AB的高度;
(2)学校要在A,E之间挂一些彩旗,请你求出A,E之间的距离(结果保留整数).
(参考数据:sin22°≈,cos22°≈,tan22°≈)
?
?
?
?
?
?
?
?
3.?如图,某校一幢教学大楼的顶部竖有一块宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.414,≈1.732)
?
?
4.?如图所示,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿到达.现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11?km,∠A=45°,∠B=37°,桥DC和AB平行,则现在从A地到B地比原来少走多少路程?(结果精确到0.1?km,参考数据:≈1.41,≈0.60,≈0.80)
?
?
?
?
?
?
?
?
5.?如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.
(说明:两问的计算结果均精确到0.1米,参考数据:≈1.41,
≈1.73,≈2.24,≈2.45)
(1)求新传送带AC的长度;
(2)若需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.
?
?
?
?
?6.?如图所示,山坡上有一棵与地面垂直的大树AB,一场大风过后,大树被刮倾斜后从点C处折断倒在山坡上,树的顶部D恰好接触到坡面AE上.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角
∠ADC=60°,AD=4?m.
(1)求∠CAE的度数;
(2)求这棵大树折断前的高度.(结果精确到个位,参考数据:
≈1.4,≈1.7,≈2.4)
?
7.?已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16?km,一艘货轮从B港口以
40?km/h的速度沿如图所示的BC方向航行,15?min后到达C处,现测得C处位于A观测点北偏东79.8°方向,求此时货轮与A观测点之间的距离AC的长.(精确到0.1?km,参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,≈1.41,≈2.24)
?
?
?
?
测量类应用题(习题)
??例题示范
例:某市为了改善市区交通状况市,计划修建一座新大桥.如图,新大桥的两端位于A,B两点,小张为了测量A,B之间的距离,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长为多少米.(结果精确到0.1米,参考数据:,)
解:由题意,∠BAC=90°,∠BDA=76.1°,∠BCA=68.2°,CD=82,设AD=a米,则AC=(a+82)米
在Rt△BAD中,∠BDA=76.1°,AD=a∴AB=4a
在Rt△BAC中,∠BCA=68.2°,AC=a+82,∴AB=2.5(a+82)∴4a=2.5(a+82).
∴米即AB的长约为546.7米.
??
??巩固练习
1.?如图,一艘轮船以每小时20海里的速度沿正北方向航行,在A处测得灯塔C位于北偏西30°的方向上,轮船继续航行2小时后到达B处,在B处测得灯塔C位于北偏西60°的方向上.当轮船到达灯塔C的正东方向上的D处时,求轮船与灯塔C的距离.(结果保留根号)
?
?
?
2.?如图,在某飞机场东西方向的地面l上有一长为1?km的飞机跑道MN,在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5千米的C处.
(1)该飞机航行的速度是多少千米/小时?(结果保留根号)
(2)如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由.
?
?
?
?
?
3.?如图,河流的两岸PQ,MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=30米,某人在河岸MN的A处测得∠DAN=30°,然后沿河岸走了50米达到B处,测得∠CBN=60°,求河流的宽度CE.
?
?
?
4.?如图,为了测量某山AB的高度,小明先在山脚C点测得山顶A的仰角为45°,然后沿坡度为的斜坡走100米到达D点,在D点测得山顶A的仰角为30°,求山AB的高度.(结果精确到0.1米,参考数据:≈1.73)
?
?
?
?
?
?
?
??
5.?小亮和课外兴趣小组的伙伴们在课外活动中观察大吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米,当吊臂顶端由A′点降落至A点(吊臂长度不变)时,所吊装的重物(大小忽略不计)从B′处恰好放到地面上的B处,紧绷着的吊缆AB=A′B′,AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=20米,且cosA,.
(1)求此重物在水平方向移动的距离BC;
(2)求此重物在竖直方向移动的距离B′C.(结果保留根号)
?
?
?
?
?
?
?
?
?
?
?
??思考小结
1.?我们已经学习过方程与不等式应用题,一次函数应用题以及测量类应用题,应用题的处理流程为:
①?理解题意,梳理信息
②?建立模型
③?求解验证,回归实际
2.?我们已经学习过相似,也学习过了三角函数,现在来思考一下它们的联系.
在学习相似三角形判定时知道“两边对应成比例且夹角相等的两个三角形相似”,
即当∠B=∠E,时,△ABC∽△DEF
?
特别地,当∠B=∠E=90°时,若,则△ABC∽△DEF
?
根据比例的性质我们知道可以改写成,而,我们得到
当∠B=∠E=90°时,若,则△ABC∽△DEF,
∠C=∠F.
借助上面的分析,请在下图中进行证明:若,则∠C=∠F.(描述辅助线,给出证明过程)
?
?
【参考答案】
??课前预习
1.?3
2.?仰角;俯角.
??知识点睛
1.?坡比,铅直高度,水平宽度.
2.?解直角三角形,结果判断.①线段,角度,直角三角形.
??精讲精练
1.?3.5米
2.?(1)教学楼AB的高度为12
m;(2)A,E之间的距离为27
m.
3.?这块宣传牌CD的高度为2.7米.
4.?比原来少走4.9
km.
5.?(1)新传送带AC的长度为5.6米;(2)需要挪走,理由略.
6.?(1)75°;(2)这棵大树折断前的高度为10?m.
7.?货轮与A观测点之间的距离AC的长为13.4
km.
【参考答案】
??巩固练习
1.?海里
2.?(1)千米/小时
(2)能,理由略
3.?米
4.?236.5米
5.?(1)6米?(2)()米
??思考小结
2.?证明略
