人教版七年级上册4.2 直线、射线、线段讲义(附答案)
文档属性
| 名称 | 人教版七年级上册4.2 直线、射线、线段讲义(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览



文档简介
直线、射线、线段(讲义)
??课前预习
1.?填空:点动成_______,线动成_______,面动成_______.
2.?画图:请你画出一条直线、一条射线、一条线段.
?
?
?
?
?
?
?
3.?试一试,经过一点O可以画_______条直线.
?
?
?
4.?经过A,B两点画直线,可以画______条,请在下图中画出经过A,B两点的所有直线.
?
??
知识点睛
1.?直线、射线、线段的表示及异同:
?
图示表示
端点个数
有无方向
能否度量
直线
?
?
?
?
射线
?
?
?
?
线段
?
?
?
?
2.?两个基本事实:
①?经过两点有一条直线,并且只有一条直线;(简单说成:______________.)
②?两点的所有连线中,线段最短.(简单说成:两点之间,______________.)
3.?连接两点间的_____________,叫做这两点的距离.
4.?比较线段长短的方法:______________、______________.
5.?线段上的点把线段分成相等的两条线段,则这个点叫做线段的________.
6.?如图,若点C为线段AB的中点,则中点的六种表示是____________________________________________________
___________________________________________________.
?
7.?几何语言书写规范:
①延长线段AB到点C,使BC=AB;
②连接AB;
③反向延长射线OA;
④取线段AB的中点O;
⑤延长线段AB交线段CD的延长线于点M.
??精讲精练
1.?下面的说法正确的是(????)
A.直线AB与直线BA是同一条直线
B.射线BA与射线AB是同一条射线
C.数轴是一条射线
D.射线是直线的一半
2.?下图有_________条线段.
?
?
?
3.?直线AB上有一点C,直线AB外有一点P,由A,B,C,P四点可以确定_________条线段.
4.?已知:如图,则下列叙述不正确的是(????)
A.点O不在直线AC上
B.射线AB与射线BC是指同一条射线
C.图中共有5条线段
D.直线AB与直线CA是指同一条直线
5.?下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程;
⑤把笔尖看成一个点,当这个点运动时便得到一条线.
其中能用“两点确定一条直线”来解释的现象有(????)
A.①⑤?B.①③?C.②④?D.③④
6.?如图所示,用“>”、“<”或“=”连接下列各式,并说明理由.AB+BC______AC,AC+BC______AB,BC_____AB+AC,理由是___________________________.
?
?
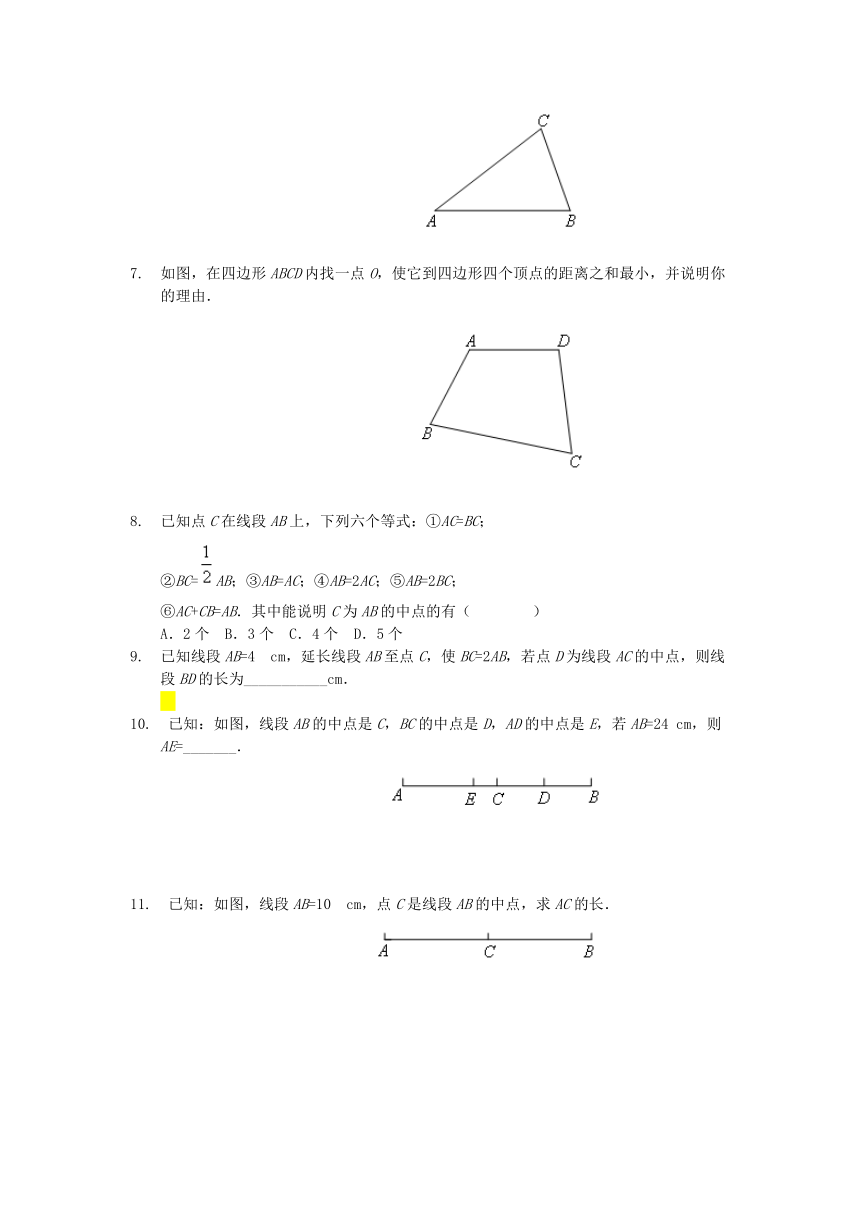
7.?如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和最小,并说明你的理由.
?
?
8.?已知点C在线段AB上,下列六个等式:①AC=BC;
②BC=AB;③AB=AC;④AB=2AC;⑤AB=2BC;
⑥AC+CB=AB.其中能说明C为AB的中点的有(????)
A.2个?B.3个?C.4个?D.5个
9.?已知线段AB=4?cm,延长线段AB至点C,使BC=2AB,若点D为线段AC的中点,则线段BD的长为___________cm.
?
10.?已知:如图,线段AB的中点是C,BC的中点是D,AD的中点是E,若AB=24
cm,则AE=_______.
?
11.?已知:如图,线段AB=10?cm,点C是线段AB的中点,求AC的长.
?
?
?
?
?
?
?
12.?已知:如图,点C是线段AB的中点,AC=4?cm,求AB的长.
?
13.?
已知:如图,线段AB=10?cm,AD=6?cm,点C是线段AD的中点,求BC的长.
?
?
?
?
?
?
?
?
14.?如图,线段AB=4,点O是线段AB上一点,点C,D分别是线段OA,OB的中点,求CD的长.
?
15.?
下列叙述:①延长直线AB到C;②延长射线AB到C;③延长线段AB到C,使BC=AC;④反向延长线段AB;⑤反向延长射线AB.其中正确的有_____________.(填序号)
16.?按要求作图:
(1)连接AB;(2)作射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一点D(点C,
D不与点A重合),作直线CD.
?
?
?
17.?如图,在同一平面内有四个点A,B,C,D.
(1)作射线CD;
(2)作直线AD;
(3)连接AB;
(4)作直线BD与直线AC相交于点O.
?
直线、射线、线段(习题)
??复习巩固
1.?关于直线、射线、线段的描述正确的是(????)
A.直线最长,线段最短
B.射线是直线长度的一半
C.直线没有端点,射线有一个端点,线段有两个端点
D.直线、射线及线段的长度都不确定
2.?下列说法中,正确的序号有______________.
①射线AB和射线BA是同一条射线;
②延长射线MN到C;
③延长线段MN到A,使NA=2MN;
④连接两点的线段长度叫做两点间的距离.
3.?如图,点A,B,C,D在同一直线上,那么图中共有(????)条射线.
A.6?B.7
C.8?D.9
4.?数学来源于生活,又应用于生活,生活中有下列现象:
①建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙;
②把弯曲的河道改直,可以缩短航程;
③木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线;
④从A地到B地架设电线,总是尽可能沿着线段AB架设.
其中能用“两点确定一条直线”来解释的现象有(????)
A.①②?B.①③?C.②④?D.③④
5.?郑州北三环北延隧道4
520米,是我省最长的隧道,可以用来解释建造隧道的目的的数学基本事实是_______________.
6.?如图,A,B,C,D,E是直线l上的五个点,则
?
(1)BD=CD+_________;(2)CE=______+_______;
(3)BE=BC+______+DE;(4)BD=AD-_____=BE-______.
7.?若点C在线段AB上,则下列等式:①AB;②AC=CB;③AB=2AC;④AC+CB=AB,其中能说明点C是线段AB中点的是_________________(填序号).
8.?点C是线段AB的中点,点D是线段BC上一点,下列说法错误的是(????)
A.?B.
C.?D.
9.?已知线段AB=2?cm,延长AB到C,使BC=2AB,若点D为AB的中点,则线段CD的长为_________.
10.?已知点C为线段AB的中点,点D为线段BC的中点,若AB=10
cm,则线段AD的长是_________.
11.?已知两根木条分别长60?cm,100?cm,将它们的一端重合,放在同一条直线上,此时两根木条的中点间的距离是______cm.
12.?已知:如图,线段BC=6?cm,点C是线段AB的中点,求AC的长.
?
?
?
?
?
?
?
?
?
13.?如图,点C,D是线段AB上两点,点D是AC的中点,若BC=6
cm,BD=10
cm,求AB的长.
?
14.?已知:如图,线段AD=8
cm,线段BC=4
cm,点E,F分别是AB,CD的中点,求EF的长.
?
?
?
?
?
?
?
?
?
?
?
15.?如图,在同一平面内有四个点A,B,C,D,按照下列语句作出图形:
①作直线AB;
②作射线BD;
③连接BC;
④线段AC和线段BD相交于点O;
⑤反向延长线段BC至E,使BE=BC.
?
?
【参考答案】
??课前预习
1.?线;面;体2.?略3.?无数4.?1,图略.
??知识点睛
1.?略
2.?①两点确定一条直线;②线段最短
3.?线段的长度
4.?度量法;重合法
5.?中点
6.?AC=BC,BC=AC,AC=AB,BC=AB,AB=2AC,AB=2BC
??精讲精练
1.?A
2.?6
3.?6
4.?B
5.?C
6.?>;>;<;两点之间,线段最短
7.?连接AC,BD,其交点O即为所求;两点之间,线段最短
8.?C
9.?2
10.?9cm
11.?5
cm
12.?8
cm
13.?7
cm
14.?2
15.?④⑤
16.?略
17.?略
【参考答案】
??复习巩固
1.?C
2.?③④
3.?C
4.?B
5.?两点之间,线段最短
6.?(1)BC;?(2)CD,DE;
(3)CD;?(4)AB,DE
7.?①②③
8.?D
9.?5
cm
10.?7.5
cm
11.?80或20
12.?6?cm
13.?14?cm
14.?6?cm
15.?略
??课前预习
1.?填空:点动成_______,线动成_______,面动成_______.
2.?画图:请你画出一条直线、一条射线、一条线段.
?
?
?
?
?
?
?
3.?试一试,经过一点O可以画_______条直线.
?
?
?
4.?经过A,B两点画直线,可以画______条,请在下图中画出经过A,B两点的所有直线.
?
??
知识点睛
1.?直线、射线、线段的表示及异同:
?
图示表示
端点个数
有无方向
能否度量
直线
?
?
?
?
射线
?
?
?
?
线段
?
?
?
?
2.?两个基本事实:
①?经过两点有一条直线,并且只有一条直线;(简单说成:______________.)
②?两点的所有连线中,线段最短.(简单说成:两点之间,______________.)
3.?连接两点间的_____________,叫做这两点的距离.
4.?比较线段长短的方法:______________、______________.
5.?线段上的点把线段分成相等的两条线段,则这个点叫做线段的________.
6.?如图,若点C为线段AB的中点,则中点的六种表示是____________________________________________________
___________________________________________________.
?
7.?几何语言书写规范:
①延长线段AB到点C,使BC=AB;
②连接AB;
③反向延长射线OA;
④取线段AB的中点O;
⑤延长线段AB交线段CD的延长线于点M.
??精讲精练
1.?下面的说法正确的是(????)
A.直线AB与直线BA是同一条直线
B.射线BA与射线AB是同一条射线
C.数轴是一条射线
D.射线是直线的一半
2.?下图有_________条线段.
?
?
?
3.?直线AB上有一点C,直线AB外有一点P,由A,B,C,P四点可以确定_________条线段.
4.?已知:如图,则下列叙述不正确的是(????)
A.点O不在直线AC上
B.射线AB与射线BC是指同一条射线
C.图中共有5条线段
D.直线AB与直线CA是指同一条直线
5.?下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程;
⑤把笔尖看成一个点,当这个点运动时便得到一条线.
其中能用“两点确定一条直线”来解释的现象有(????)
A.①⑤?B.①③?C.②④?D.③④
6.?如图所示,用“>”、“<”或“=”连接下列各式,并说明理由.AB+BC______AC,AC+BC______AB,BC_____AB+AC,理由是___________________________.
?
?
7.?如图,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和最小,并说明你的理由.
?
?
8.?已知点C在线段AB上,下列六个等式:①AC=BC;
②BC=AB;③AB=AC;④AB=2AC;⑤AB=2BC;
⑥AC+CB=AB.其中能说明C为AB的中点的有(????)
A.2个?B.3个?C.4个?D.5个
9.?已知线段AB=4?cm,延长线段AB至点C,使BC=2AB,若点D为线段AC的中点,则线段BD的长为___________cm.
?
10.?已知:如图,线段AB的中点是C,BC的中点是D,AD的中点是E,若AB=24
cm,则AE=_______.
?
11.?已知:如图,线段AB=10?cm,点C是线段AB的中点,求AC的长.
?
?
?
?
?
?
?
12.?已知:如图,点C是线段AB的中点,AC=4?cm,求AB的长.
?
13.?
已知:如图,线段AB=10?cm,AD=6?cm,点C是线段AD的中点,求BC的长.
?
?
?
?
?
?
?
?
14.?如图,线段AB=4,点O是线段AB上一点,点C,D分别是线段OA,OB的中点,求CD的长.
?
15.?
下列叙述:①延长直线AB到C;②延长射线AB到C;③延长线段AB到C,使BC=AC;④反向延长线段AB;⑤反向延长射线AB.其中正确的有_____________.(填序号)
16.?按要求作图:
(1)连接AB;(2)作射线OA,射线OB;
(3)在线段AB上取一点C,在射线OA上取一点D(点C,
D不与点A重合),作直线CD.
?
?
?
17.?如图,在同一平面内有四个点A,B,C,D.
(1)作射线CD;
(2)作直线AD;
(3)连接AB;
(4)作直线BD与直线AC相交于点O.
?
直线、射线、线段(习题)
??复习巩固
1.?关于直线、射线、线段的描述正确的是(????)
A.直线最长,线段最短
B.射线是直线长度的一半
C.直线没有端点,射线有一个端点,线段有两个端点
D.直线、射线及线段的长度都不确定
2.?下列说法中,正确的序号有______________.
①射线AB和射线BA是同一条射线;
②延长射线MN到C;
③延长线段MN到A,使NA=2MN;
④连接两点的线段长度叫做两点间的距离.
3.?如图,点A,B,C,D在同一直线上,那么图中共有(????)条射线.
A.6?B.7
C.8?D.9
4.?数学来源于生活,又应用于生活,生活中有下列现象:
①建筑工人砌墙时,经常先在两端立桩拉线,然后沿着线砌墙;
②把弯曲的河道改直,可以缩短航程;
③木匠师傅锯木料时,一般先在木板上画出两个点,然后过这两点弹出一条墨线;
④从A地到B地架设电线,总是尽可能沿着线段AB架设.
其中能用“两点确定一条直线”来解释的现象有(????)
A.①②?B.①③?C.②④?D.③④
5.?郑州北三环北延隧道4
520米,是我省最长的隧道,可以用来解释建造隧道的目的的数学基本事实是_______________.
6.?如图,A,B,C,D,E是直线l上的五个点,则
?
(1)BD=CD+_________;(2)CE=______+_______;
(3)BE=BC+______+DE;(4)BD=AD-_____=BE-______.
7.?若点C在线段AB上,则下列等式:①AB;②AC=CB;③AB=2AC;④AC+CB=AB,其中能说明点C是线段AB中点的是_________________(填序号).
8.?点C是线段AB的中点,点D是线段BC上一点,下列说法错误的是(????)
A.?B.
C.?D.
9.?已知线段AB=2?cm,延长AB到C,使BC=2AB,若点D为AB的中点,则线段CD的长为_________.
10.?已知点C为线段AB的中点,点D为线段BC的中点,若AB=10
cm,则线段AD的长是_________.
11.?已知两根木条分别长60?cm,100?cm,将它们的一端重合,放在同一条直线上,此时两根木条的中点间的距离是______cm.
12.?已知:如图,线段BC=6?cm,点C是线段AB的中点,求AC的长.
?
?
?
?
?
?
?
?
?
13.?如图,点C,D是线段AB上两点,点D是AC的中点,若BC=6
cm,BD=10
cm,求AB的长.
?
14.?已知:如图,线段AD=8
cm,线段BC=4
cm,点E,F分别是AB,CD的中点,求EF的长.
?
?
?
?
?
?
?
?
?
?
?
15.?如图,在同一平面内有四个点A,B,C,D,按照下列语句作出图形:
①作直线AB;
②作射线BD;
③连接BC;
④线段AC和线段BD相交于点O;
⑤反向延长线段BC至E,使BE=BC.
?
?
【参考答案】
??课前预习
1.?线;面;体2.?略3.?无数4.?1,图略.
??知识点睛
1.?略
2.?①两点确定一条直线;②线段最短
3.?线段的长度
4.?度量法;重合法
5.?中点
6.?AC=BC,BC=AC,AC=AB,BC=AB,AB=2AC,AB=2BC
??精讲精练
1.?A
2.?6
3.?6
4.?B
5.?C
6.?>;>;<;两点之间,线段最短
7.?连接AC,BD,其交点O即为所求;两点之间,线段最短
8.?C
9.?2
10.?9cm
11.?5
cm
12.?8
cm
13.?7
cm
14.?2
15.?④⑤
16.?略
17.?略
【参考答案】
??复习巩固
1.?C
2.?③④
3.?C
4.?B
5.?两点之间,线段最短
6.?(1)BC;?(2)CD,DE;
(3)CD;?(4)AB,DE
7.?①②③
8.?D
9.?5
cm
10.?7.5
cm
11.?80或20
12.?6?cm
13.?14?cm
14.?6?cm
15.?略
