青岛版数学七年级上册课件:7.2一元一次方程(17张PPT)
文档属性
| 名称 | 青岛版数学七年级上册课件:7.2一元一次方程(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 331.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览






文档简介
7.2一元一次方程
等式两边都加上(或减去)同一个整式,所得的结果仍是等式。
如果a=b,那么a+c=b+c , a-c=b-c
复习
如果a=b, 那么ac=bc.
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式。
如果a=b,那么
基本性质1:
基本性质2:
等式还具有以下性质:
1、如果a=b,那么b=a.
例:如果3=x,那么
如果x=y,且y=-2,那么
2、如果a=b,且b=c,那么a=c.
x=3.
x=-2.
学习目标:
1、记住一元一次方程的定义,会识别一元一次方程。
2、经历探索一元一次方程解的过程,
(一)情境导入
“猜猜小明的年龄”
小明是10月出生,他的年龄加上7,正好是他出生的月份数的2倍,请你们猜猜小明的年龄大约是多少?
设小明的年龄为x岁,那么年龄加上7就______ ,而这个式子等于月份10的2倍即______ 。据这个等量关系,我们可以得到方程____________。
x+7
10×2
x+7=10×2
实验与探究
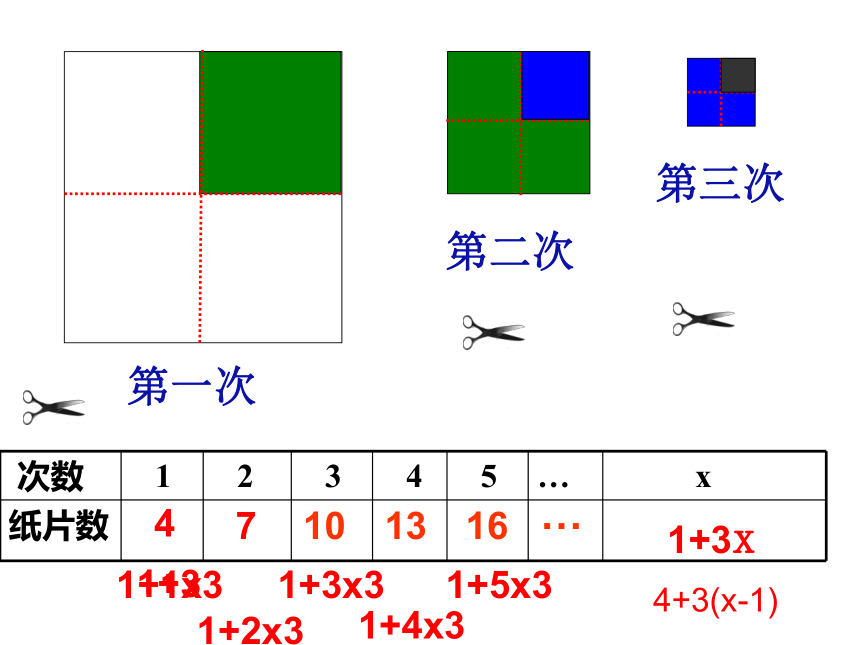
取一张纸,第一次将它剪成4片,第二次再将其中的一片剪成更小的4片,继续这样剪下去,如图。
(1)第三次,第四次,第五次,……分别
共剪得多少张纸片?填下表:
次数
1
2
3
4
5
…
纸片数
第一次
第二次
第三次
次数
1
2
3
4
5
…
x
纸片数
10
13
16
…
4
7
1+1x3
1+2x3
1+3x3
1+4x3
1+5x3
1+3x
1+3
4+3(x-1)
实验与探究
(2)如果剪了x次(x是正整数),那么共剪得多少张纸片?你是怎样得到的?与同学交流。
(3)如果剪得的纸片共64片,一共剪了多少次?
这时剪纸的次数x是未知数,问题中给出的等量关系是:
剪x次共剪得的纸片数=64
剪x次共能剪得(3x+1)片
剪x次共能剪得[4+3(x-1 )]片
3x+1=64
4+3(x-1)=64
观察下列方程,有什么特点?
3x+1=64 4+3(x-1)=64 3+x-8=29
方程的两边都是整式,都只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程。
注意:(1)元”即为未知数,未知数可以
是x,y.z等
(2)未知数的个数:一个
(3)未知数的次数:次数都是1
1.判断下列方程是否是一元一次方程,为什么?(抢答)
(1)x+y=1 (2)3x2=x
(3)3x-2=1 (4)2(y-1)=y+3
(5)xy-2=1+x
2.若2xn-1-3=8是一元一次方程,则n的值为( )
跟踪训练
√
×
×
√
×
×
2
将x=-1代入方程3x+5=2,左边=右边
使方程的两边相等的未知数的值叫做方程的解。
如:x=-1是方程3x+5=2的解,x=2是方程-2x+5x=6的解。
练习:1、方程2x-5=1的解( )
A 3 B -3 C 2 D -2
2、下列方程中,解是x=4的方程是( )
A 2x+5=10 B -3x-8=-4
C 0.5+3=2x-3 D 2(x-1)=3x-6
D
A
方程的解:
只含有一个未知数的方程的解也叫做 方程的根。
求方程解的过程叫做解方程。
解方程就是将方程化为x=a的形式
方程的根:
解方程:
要求:(1)未知数x在等号的左边,常数项在等号的右边,
(2)x的系数为1.
怎样求方程4+3(x-1)=64的解呢?
X(次)
纸片数(片)
与64片比较
估算第一次
估算第二次
估算第三次
估算第四次
10
31
少了
25
76
多了
21
64
相等
用估算法估算x+7=2 × 10的解。
X
x+7
与2×10比较
估算第一次
估算第二次
估算第三次
方程3x-2=x+2的解( )
A 2 B -1.5 C 1.5 D -2
想一想
A
5
12
小了
10
17
13
20
小了
相等
验证法
1 下列方程是一元一次方程的是( )
(1) 2x-1=0 (2) 2x-y=3 (3) x2-16=0 (4) 4(t-1)=2(3t+1)
2 若2xn-2-4=9是一元一次方程,则n的值为( )
3 方程3x-2=-5(x-2)的解( )
A-1.5 B 1.5 C 1 D -1
4 估算5x-3=12的解。
达标测试
(1) (4)
3
B
3
本节课你学到了 知识
本节课你学到了 方法
你还有哪些问题没有解决
课堂小结
习题7.2的第1、3题
作业
等式两边都加上(或减去)同一个整式,所得的结果仍是等式。
如果a=b,那么a+c=b+c , a-c=b-c
复习
如果a=b, 那么ac=bc.
等式两边都乘(或除以)同一个数(除数不能为零),所得的结果仍是等式。
如果a=b,那么
基本性质1:
基本性质2:
等式还具有以下性质:
1、如果a=b,那么b=a.
例:如果3=x,那么
如果x=y,且y=-2,那么
2、如果a=b,且b=c,那么a=c.
x=3.
x=-2.
学习目标:
1、记住一元一次方程的定义,会识别一元一次方程。
2、经历探索一元一次方程解的过程,
(一)情境导入
“猜猜小明的年龄”
小明是10月出生,他的年龄加上7,正好是他出生的月份数的2倍,请你们猜猜小明的年龄大约是多少?
设小明的年龄为x岁,那么年龄加上7就______ ,而这个式子等于月份10的2倍即______ 。据这个等量关系,我们可以得到方程____________。
x+7
10×2
x+7=10×2
实验与探究
取一张纸,第一次将它剪成4片,第二次再将其中的一片剪成更小的4片,继续这样剪下去,如图。
(1)第三次,第四次,第五次,……分别
共剪得多少张纸片?填下表:
次数
1
2
3
4
5
…
纸片数
第一次
第二次
第三次
次数
1
2
3
4
5
…
x
纸片数
10
13
16
…
4
7
1+1x3
1+2x3
1+3x3
1+4x3
1+5x3
1+3x
1+3
4+3(x-1)
实验与探究
(2)如果剪了x次(x是正整数),那么共剪得多少张纸片?你是怎样得到的?与同学交流。
(3)如果剪得的纸片共64片,一共剪了多少次?
这时剪纸的次数x是未知数,问题中给出的等量关系是:
剪x次共剪得的纸片数=64
剪x次共能剪得(3x+1)片
剪x次共能剪得[4+3(x-1 )]片
3x+1=64
4+3(x-1)=64
观察下列方程,有什么特点?
3x+1=64 4+3(x-1)=64 3+x-8=29
方程的两边都是整式,都只含有一个未知数,并且未知数的次数都是1,这样的方程叫做一元一次方程。
注意:(1)元”即为未知数,未知数可以
是x,y.z等
(2)未知数的个数:一个
(3)未知数的次数:次数都是1
1.判断下列方程是否是一元一次方程,为什么?(抢答)
(1)x+y=1 (2)3x2=x
(3)3x-2=1 (4)2(y-1)=y+3
(5)xy-2=1+x
2.若2xn-1-3=8是一元一次方程,则n的值为( )
跟踪训练
√
×
×
√
×
×
2
将x=-1代入方程3x+5=2,左边=右边
使方程的两边相等的未知数的值叫做方程的解。
如:x=-1是方程3x+5=2的解,x=2是方程-2x+5x=6的解。
练习:1、方程2x-5=1的解( )
A 3 B -3 C 2 D -2
2、下列方程中,解是x=4的方程是( )
A 2x+5=10 B -3x-8=-4
C 0.5+3=2x-3 D 2(x-1)=3x-6
D
A
方程的解:
只含有一个未知数的方程的解也叫做 方程的根。
求方程解的过程叫做解方程。
解方程就是将方程化为x=a的形式
方程的根:
解方程:
要求:(1)未知数x在等号的左边,常数项在等号的右边,
(2)x的系数为1.
怎样求方程4+3(x-1)=64的解呢?
X(次)
纸片数(片)
与64片比较
估算第一次
估算第二次
估算第三次
估算第四次
10
31
少了
25
76
多了
21
64
相等
用估算法估算x+7=2 × 10的解。
X
x+7
与2×10比较
估算第一次
估算第二次
估算第三次
方程3x-2=x+2的解( )
A 2 B -1.5 C 1.5 D -2
想一想
A
5
12
小了
10
17
13
20
小了
相等
验证法
1 下列方程是一元一次方程的是( )
(1) 2x-1=0 (2) 2x-y=3 (3) x2-16=0 (4) 4(t-1)=2(3t+1)
2 若2xn-2-4=9是一元一次方程,则n的值为( )
3 方程3x-2=-5(x-2)的解( )
A-1.5 B 1.5 C 1 D -1
4 估算5x-3=12的解。
达标测试
(1) (4)
3
B
3
本节课你学到了 知识
本节课你学到了 方法
你还有哪些问题没有解决
课堂小结
习题7.2的第1、3题
作业
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
