人教版八年级上册:14.4.2完全平方公式 课件(26张PPT)
文档属性
| 名称 | 人教版八年级上册:14.4.2完全平方公式 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览







文档简介
完全平方公式
回顾与思考
公式的结构特征:
左边是
a2 ? b2;
两个二项式的乘积,
平方差公式
应用平方差公式的注意事:
回顾 & 思考
?
(a+b)(a?b)=
即两数和与这两数差的积.
右边是
两数的平方差.
?
弄清在什么情况下才能使用平方差公式:
完 全 平 方 公 式
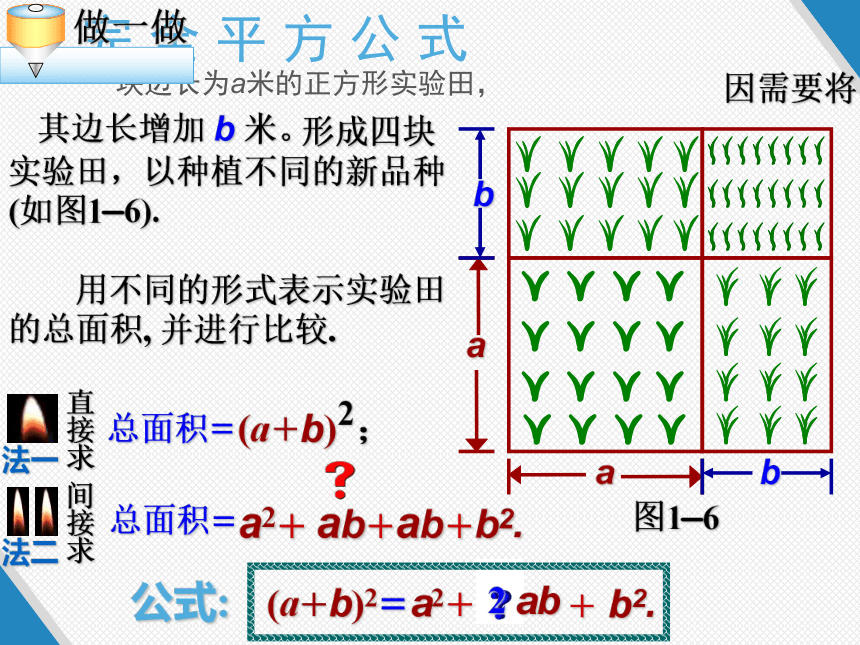
一块边长为a米的正方形实验田,
做一做
图1—6
a
因需要将其边长增加 b 米。
形成四块实验田,以种植不同的新品种(如图1—6).
用不同的形式表示实验田的总面积, 并进行比较.
a
b
b
法一
直
接
求
总面积=
(a+b) ;
2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
2
公式:
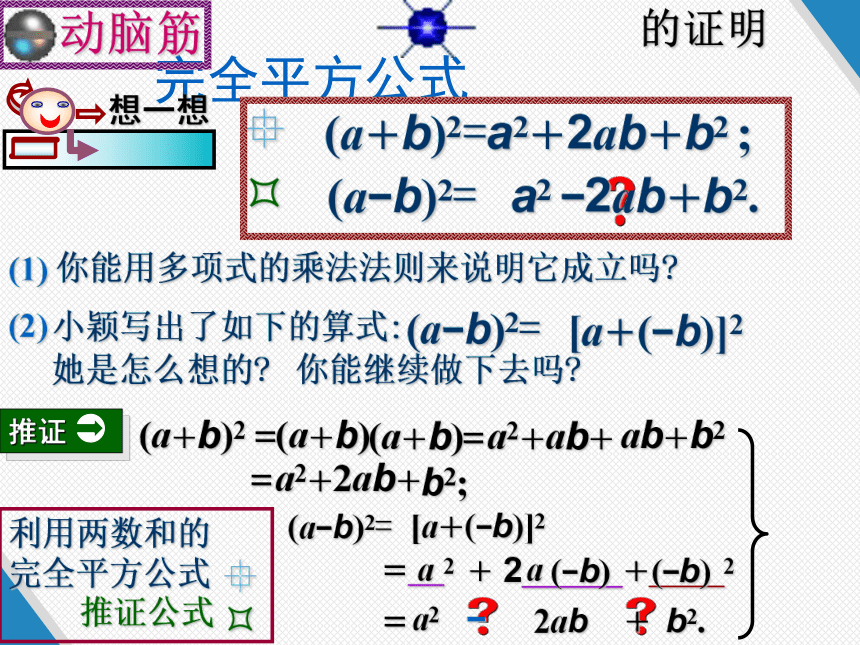
完全平方公式
动脑筋
(1) 你能用多项式的乘法法则来说明它成立吗?
想一想
(a+b)2=a2+2ab+b2 ;
(a+b)2 =
推证 ?
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
(2)
a2 ?2ab+b2.
小颖写出了如下的算式:
(a?b)2=
[a+(?b)]2
?
(a?b)2=
?
她是怎么想的?
利用两数和的
完全平方公式
?
推证公式
?
(a?b)2=
[a+(?b)]2
= 2 + 2 + 2
a
a
(?b)
(?b)
=
a2
2ab
?
b2.
+
你能继续做下去吗?
的证明
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间的符 号相同。
首平方,末平方,首尾两倍中间放,符号与前一个样
解: (4m+n)2=
(a+b)2=a2+2ab+b2
(1)(4m+n)2
( a+ b)2= a2 + 2 a b + b2
=16m2+8mn+n2
(4m)2+2 4m ·n + n2
例1 运用完全平方公式计算:
例1.运用完全平方公式计算:
(1) (4a-b)2 (2)(y+ )2
哪一部分相当于公式里的a,哪一部分相当于公式里的b呢?
例1.运用完全平方公式计算:
(1) (4a-b)2 (2)(y+ )2
=(4a)2-2?4a?b+b2
(2)(y+ )2
解:(1)(4a-b)2
=16a2-8ab+b2
=y2+y+
(1) (2x+3y)2
(2) (2x-3y)2
(3) (-2x+3y)2
(4) (-2x-3y)2
小结:当所给的二项式中两项符号相同时,一般选用“和”的完全平方公式;
当所给的二项式中两项的符号相反时,一般选用“差”的完全平方差公式.
变一变,你还能做吗?
?思考
(a+b)2 与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2 与 a2-b2相等吗?
不相等
相等
相等
解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
一试身手
(1) (y-5)2
1、利用完全平方公式计算:
(2) (-4x+2y)2.
(3) (-2n -3)2 ;
(4) ( x ? 2y)2 ;
填空:
-2x
4
-4ab
综合尝试,实践应用
-2ab
下列计算是否正确?如不正确,应怎样改正?
1.(a-2)2=a2-4 ( )
2.(2x+5)2=2x2+20x+25 ( )
3. (6a+3b)2=36a2 +18ab+9b2 ( )
4. (-a-b)(a+b)=-a2-2ab-b2 ( )
×
×
×
对
让我们大家一起来想!
如果x2-6x+N是一个完全平方式,那么N是( )
(A )-3 (B)3 (C)-9 (D)9
D
运用公式计算:
1.(a-b)(a+b)(a2+b2)
2.(2-1)(2+1)(22+1) (24+1)…… (232+1)+1
计算:
20202-2019×2021
解:原式=20202-(2020+1)(2020-1)
=20202-(20202-1)
=20202-20202+1
=1
=1002+2×100×3+32
(2) 1992 =(200-1)2
解:(1) 1032 =(100+3)2
=10000+400+9=10 409
=2002-2200+12
例2.运用完全平方公式计算:
(1) 1032 ; (2)1992
=40000-400+1=39601
你能又快又准的算出下列各式的结果吗?
计算:
1.(a+b+c)2
2.(x+2y-3)(x+2y+3)
巩固练习:
1.下列各式哪些可用完全平方公式计算
(1)(2a-3b)(3b-2a) (2)(2a-3b)(-3b-2a)
(3)(-2m+n)(2m+n) (4)(2m+n)(-2m-n)
2.错例分析:
(1)(a+b)2=a2+b2 (2)(a-b)2=a2-b2
本节课你的收获是什么?
本节课你学到了什么?
注意完全平方公式和平方差公式不同:
形式不同.
结果不同:
完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;
平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2.
有时需要进行变形,使变形后的式子符合应用完全平方公式的条件,即为“两数和(或差)的平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;a,b数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键
4
计算数的平方时,可考虑把数分成两数的和(或差),
再用完全平方公式来计算,往往带来方便。
你能根据下图中的面积说明完全平方公式吗?
感悟提升
几何解释:
a
a
b
b
=
+
+
+
a2
ab
ab
b2
(a+b)2= .
a2+2ab+b2
和的完全平方公式:
(a+b)2
=
a2
?ab
?b(a?b)
=
a2?2ab+b2 .
=
(a?b)2
a?b
a?b
a
a
ab
b(a?b)
b
b
(a?b)2
几何解释:
(a-b)2= .
a2-2ab+b2
数形结合思想
(a-b)2
差的完全平方公式:
1.(2x+y-z)(2x-y+z)
2.(a+2b-1)2
试试身手!
思考
(1) (a+b)2与(-a-b)2相等吗?
(2) (a-b)2与(b-a)2相等吗?
(3) (a-b)2与a2-b2相等吗?
回顾与思考
公式的结构特征:
左边是
a2 ? b2;
两个二项式的乘积,
平方差公式
应用平方差公式的注意事:
回顾 & 思考
?
(a+b)(a?b)=
即两数和与这两数差的积.
右边是
两数的平方差.
?
弄清在什么情况下才能使用平方差公式:
完 全 平 方 公 式
一块边长为a米的正方形实验田,
做一做
图1—6
a
因需要将其边长增加 b 米。
形成四块实验田,以种植不同的新品种(如图1—6).
用不同的形式表示实验田的总面积, 并进行比较.
a
b
b
法一
直
接
求
总面积=
(a+b) ;
2
法二
间
接
求
总面积=
a2+
ab+
ab+
b2.
(a+b)2=
a2+
ab
+
b2.
2
公式:
完全平方公式
动脑筋
(1) 你能用多项式的乘法法则来说明它成立吗?
想一想
(a+b)2=a2+2ab+b2 ;
(a+b)2 =
推证 ?
(a+b)
(a+b)
=a2+ab+
ab+b2
=a2+2ab+
b2;
(2)
a2 ?2ab+b2.
小颖写出了如下的算式:
(a?b)2=
[a+(?b)]2
?
(a?b)2=
?
她是怎么想的?
利用两数和的
完全平方公式
?
推证公式
?
(a?b)2=
[a+(?b)]2
= 2 + 2 + 2
a
a
(?b)
(?b)
=
a2
2ab
?
b2.
+
你能继续做下去吗?
的证明
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式中间的符 号相同。
首平方,末平方,首尾两倍中间放,符号与前一个样
解: (4m+n)2=
(a+b)2=a2+2ab+b2
(1)(4m+n)2
( a+ b)2= a2 + 2 a b + b2
=16m2+8mn+n2
(4m)2+2 4m ·n + n2
例1 运用完全平方公式计算:
例1.运用完全平方公式计算:
(1) (4a-b)2 (2)(y+ )2
哪一部分相当于公式里的a,哪一部分相当于公式里的b呢?
例1.运用完全平方公式计算:
(1) (4a-b)2 (2)(y+ )2
=(4a)2-2?4a?b+b2
(2)(y+ )2
解:(1)(4a-b)2
=16a2-8ab+b2
=y2+y+
(1) (2x+3y)2
(2) (2x-3y)2
(3) (-2x+3y)2
(4) (-2x-3y)2
小结:当所给的二项式中两项符号相同时,一般选用“和”的完全平方公式;
当所给的二项式中两项的符号相反时,一般选用“差”的完全平方差公式.
变一变,你还能做吗?
?思考
(a+b)2 与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
(a-b)2 与 a2-b2相等吗?
不相等
相等
相等
解题时常用结论:
(-a-b)2 =(a+b)2 (a-b)2 =(b-a)2
一试身手
(1) (y-5)2
1、利用完全平方公式计算:
(2) (-4x+2y)2.
(3) (-2n -3)2 ;
(4) ( x ? 2y)2 ;
填空:
-2x
4
-4ab
综合尝试,实践应用
-2ab
下列计算是否正确?如不正确,应怎样改正?
1.(a-2)2=a2-4 ( )
2.(2x+5)2=2x2+20x+25 ( )
3. (6a+3b)2=36a2 +18ab+9b2 ( )
4. (-a-b)(a+b)=-a2-2ab-b2 ( )
×
×
×
对
让我们大家一起来想!
如果x2-6x+N是一个完全平方式,那么N是( )
(A )-3 (B)3 (C)-9 (D)9
D
运用公式计算:
1.(a-b)(a+b)(a2+b2)
2.(2-1)(2+1)(22+1) (24+1)…… (232+1)+1
计算:
20202-2019×2021
解:原式=20202-(2020+1)(2020-1)
=20202-(20202-1)
=20202-20202+1
=1
=1002+2×100×3+32
(2) 1992 =(200-1)2
解:(1) 1032 =(100+3)2
=10000+400+9=10 409
=2002-2200+12
例2.运用完全平方公式计算:
(1) 1032 ; (2)1992
=40000-400+1=39601
你能又快又准的算出下列各式的结果吗?
计算:
1.(a+b+c)2
2.(x+2y-3)(x+2y+3)
巩固练习:
1.下列各式哪些可用完全平方公式计算
(1)(2a-3b)(3b-2a) (2)(2a-3b)(-3b-2a)
(3)(-2m+n)(2m+n) (4)(2m+n)(-2m-n)
2.错例分析:
(1)(a+b)2=a2+b2 (2)(a-b)2=a2-b2
本节课你的收获是什么?
本节课你学到了什么?
注意完全平方公式和平方差公式不同:
形式不同.
结果不同:
完全平方公式的结果 是三项,
即 (a ?b)2=a2 ?2ab+b2;
平方差公式的结果 是两项,
即 (a+b)(a?b)=a2?b2.
有时需要进行变形,使变形后的式子符合应用完全平方公式的条件,即为“两数和(或差)的平方”,然后应用公式计算.
在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2;a,b数是乘积被平方时要注意添括号, 是运用完全平方公式进行多项式乘法的关键
4
计算数的平方时,可考虑把数分成两数的和(或差),
再用完全平方公式来计算,往往带来方便。
你能根据下图中的面积说明完全平方公式吗?
感悟提升
几何解释:
a
a
b
b
=
+
+
+
a2
ab
ab
b2
(a+b)2= .
a2+2ab+b2
和的完全平方公式:
(a+b)2
=
a2
?ab
?b(a?b)
=
a2?2ab+b2 .
=
(a?b)2
a?b
a?b
a
a
ab
b(a?b)
b
b
(a?b)2
几何解释:
(a-b)2= .
a2-2ab+b2
数形结合思想
(a-b)2
差的完全平方公式:
1.(2x+y-z)(2x-y+z)
2.(a+2b-1)2
试试身手!
思考
(1) (a+b)2与(-a-b)2相等吗?
(2) (a-b)2与(b-a)2相等吗?
(3) (a-b)2与a2-b2相等吗?
