人教版数学九年级下册第二十七章 相似模型讲义(二)(含简单答案)
文档属性
| 名称 | 人教版数学九年级下册第二十七章 相似模型讲义(二)(含简单答案) |  | |
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 14:47:54 | ||
图片预览

文档简介
相似模型(二)(讲义)
??课前预习
1.?按要求解决下列问题:
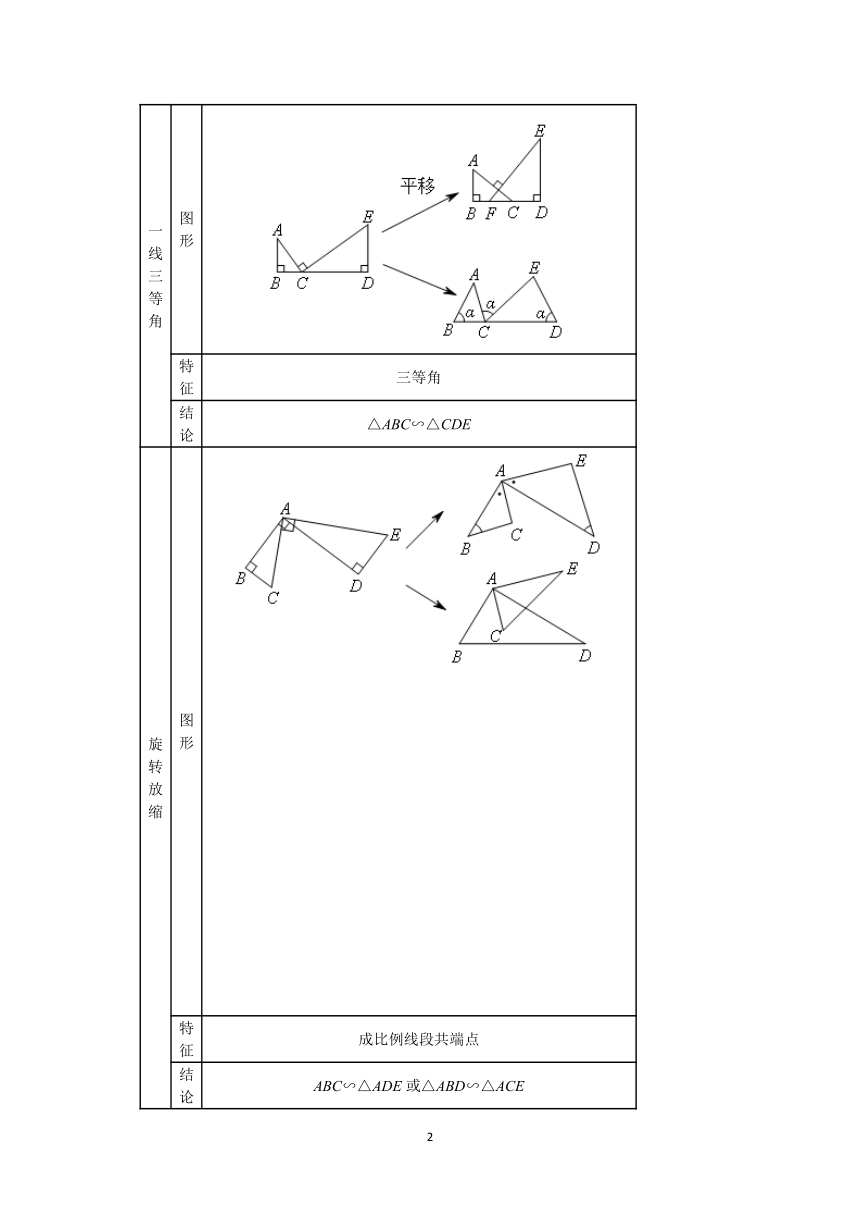
①如图,AB⊥BD于点B,ED⊥BD于点D,点C是线段BD上一点,连接AC,CE,AC⊥CE.求证:△ABC∽△CDE.
?
②如图,将两个全等的等腰直角三角形如图摆放(顶点A重合),所有的点都在同一平面内.请找出图中的相似三角形(不包括全等).
?
③如图,已知A是等边三角形PQR的边RQ延长线上的点,B是QR延长线上的点.若∠APB=120°,请找出图中的相似三角形.
?
??知识点睛
1.?相似综合模型
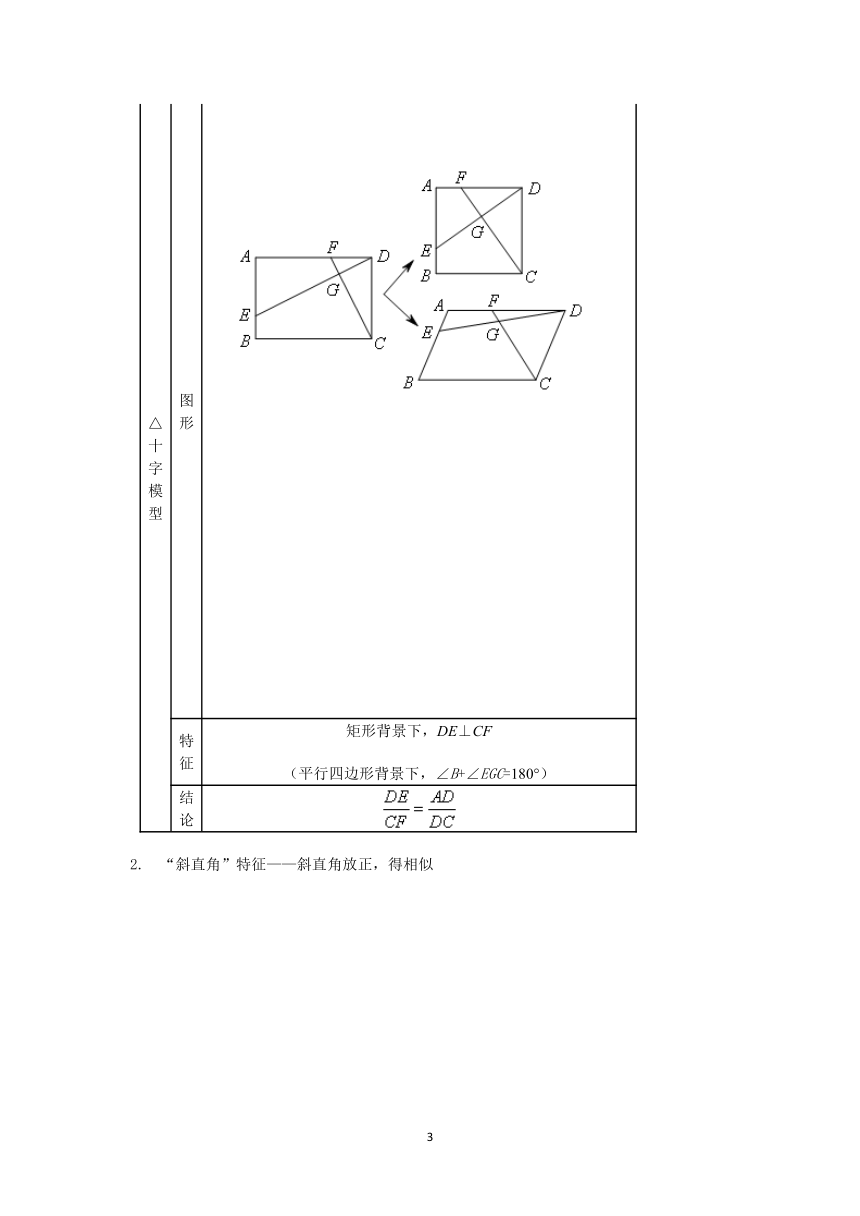
一线三等角
图形
?
特征
三等角
结论
△ABC∽△CDE
旋转放缩
图形
?????????
特征
成比例线段共端点
结论
ABC∽△ADE或△ABD∽△ACE
△十字模型
图形
?????????
特征
矩形背景下,DE⊥CF(平行四边形背景下,∠B+∠EGC=180°)
结论
2.?“斜直角”特征——斜直角放正,得相似
?????
3.?“相似”与“∽”
“相似”与“∽”的区别在于两个三角形的对应关系是否确定.“相似”只能表示两个三角形的形状相同,但对应关系不确定;出现“相似”时,一般需要分类讨论.
??精讲精练
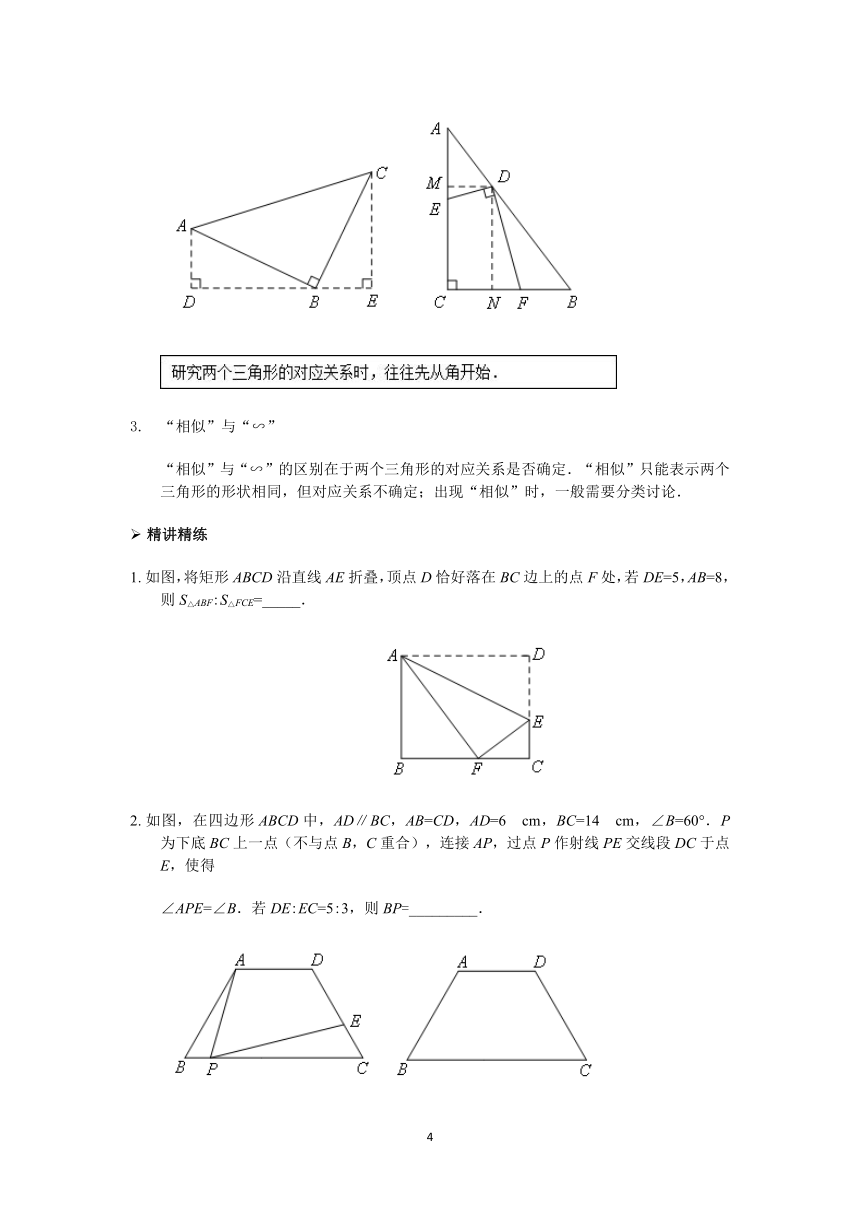
1.?如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,若DE=5,AB=8,则S△ABF:S△FCE=_____.
?
2.?如图,在四边形ABCD中,AD∥BC,AB=CD,AD=6?cm,BC=14?cm,∠B=60°.P为下底BC上一点(不与点B,C重合),连接AP,过点P作射线PE交线段DC于点E,使得
∠APE=∠B.若DE:EC=5:3,则BP=_________.
??
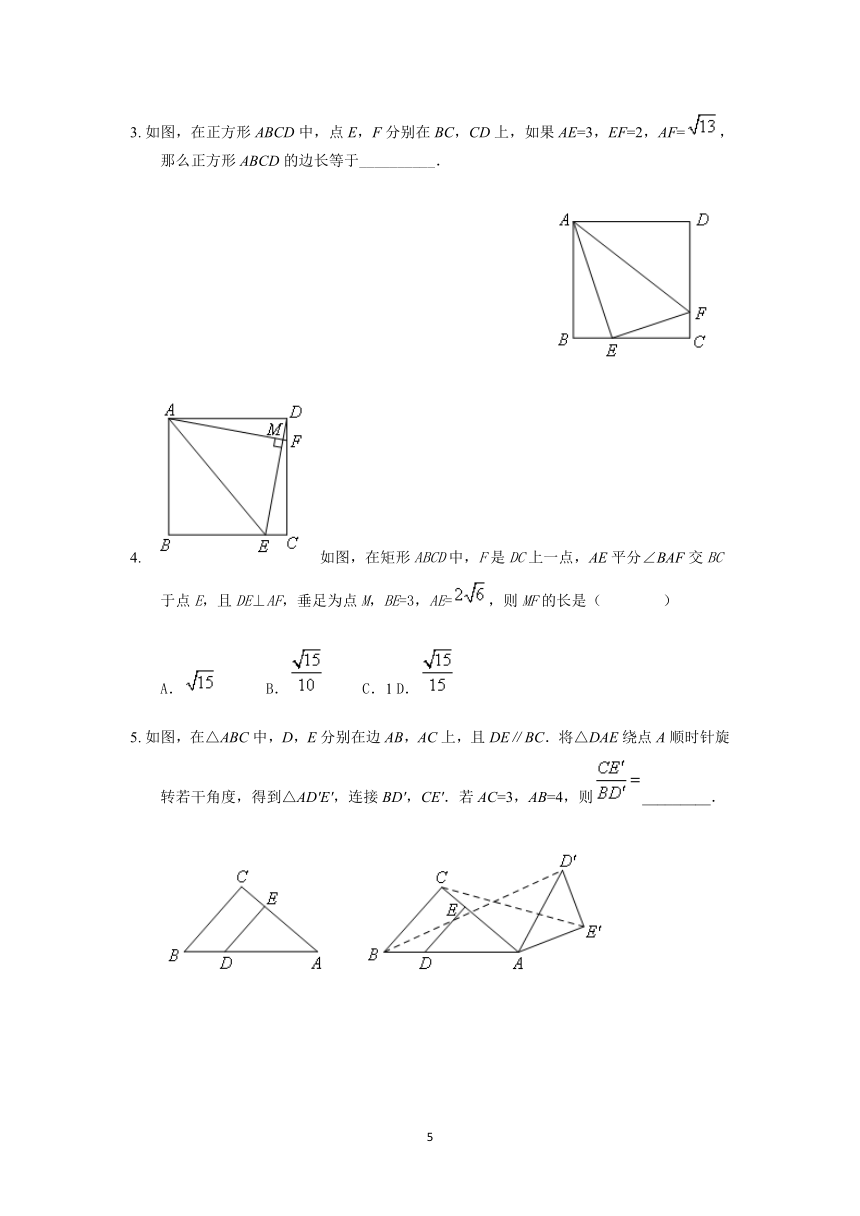
3.?如图,在正方形ABCD中,点E,F分别在BC,CD上,如果AE=3,EF=2,AF=,那么正方形ABCD的边长等于__________.
?
4.?如图,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=,则MF的长是(????)
A.?
B.
C.1?D.?
5.?如图,在△ABC中,D,E分别在边AB,AC上,且DE∥BC.将△DAE绕点A顺时针旋转若干角度,得到△AD′E′,连接BD′,CE′.若AC=3,AB=4,则_________.
?
6.?如图,在Rt△ABC中,∠ACB=90°,BC=9,AC=6,CD⊥AB于点D,点E是线段AC上一动点,连接DE,过点D作FD⊥ED,交线段BC于点F,连接EF.若EC=2,则EF=_____.
?
?如图,矩形ABCD中,AD=nAB,E,F,G,H分别是AB,BC,CD,AD边上的点,
EG⊥FH.
(1)当n=1,FH=3时,EG=___________;
(2)当n=2,FH=时,四边形EFGH的面积为_______.
?
8.?在矩形ABCD中,AB=4,BC=3,点P在线段AB上.若将
△DAP沿DP折叠,使点A落在矩形对角线AC上的A′处,则AP的长为_____________.
9.?矩形纸片ABCD中,AB=5,AD=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.若CB′为1,则AE的长为___________.
?
10.?如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为(????)
A.18?B.?C.?D.
??
11.?在平面直角坐标系中,将一含30°角的直角三角板放置在坐标系中.
(1)如图1,若该三角板直角顶点与原点O重合,顶点A的坐标为(-1,2),∠ABO=30°,顶点B在第一象限,则点B的坐标为_______.
(2)如图2,若该三角板直角顶点落在点C(2,2),顶点A的坐标为(3,0),∠ABC=30°,顶点B在第一象限,则点B的坐标为___________.
???
图1
??????????????????
????图2
12.?如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=,则BD的长为___________.
?
13.?在下图中,根据线段DE补全△DEF,使得△DEF与△ABC相似.(△DEF的顶点F在直线DE的上方)
?
?
14.?将三角形纸片ABC按如图1所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,则BF=___________.
?
图1
????????????????????备用图
?
15.?如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止运动,设运动时间为t秒.当以B,D,E为顶点的三角形与△ABC相似时,则t的值为________.
?
16.?如图,在梯形ABCD中,AB∥CD,∠B=∠C=90°,点E在BC边上,AB=3,CD=2,BC=7.若△ABE与△ECD相似,则CE=___________.
?
相似模型(二)(习题)
??复习巩固
1.?如图,等腰Rt△ABC的直角边长为3,P为斜边BC上一点,且BP=,D为AC上一点.若∠APD=45°,则CD=______.
?
2.?如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=.点P在线段AB上,若△PCD是以点P为直角顶点的直角三角形,则AP=__________.
?
3.?如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置.若点B的坐标为(2,4),则点D的坐标是__________.
?
4.?如图,在矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交CD于点F,连接AF.设,则给出下列结论:①△ABE∽△ECF;②AE平分∠BAF;③当k=1时,△ABE∽△ADF.其中正确的是_____________.
?
5.?如图,在矩形ABCD中,E,N,F,M分别是边AB,BC,CD,DA上的点,且EF⊥MN,求证:.
?
?
?
6.?如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,有下列说法:①AC⊥DE;②∠BCE=∠ACD;
③△AED∽△ECB;④△AFE∽△DFC;⑤AD∥BC;⑥四边形ABCD面积的最大值为.其中正确的是__________.
?
7.?如图,D是Rt△ABC的斜边AB上一点,点E在AC上,连接DE,CD,且∠ADE=∠BCD,CF⊥CD交DE的延长线于点F,连接AF.求证:AF⊥AB.
?
8.?如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是AC上的点,若AF⊥BE,垂足为F.求证:∠BFD=∠C.
?
9.?
如图,在△ABC中,AB=AC,AD⊥BC,DE⊥AC,M为DE的中点,AM与BE相交于点N,AD与BE相交于点F.
求证:(1);
(2)△BCE∽△ADM;
(3)猜想AM与BE的位置关系,并说明理由.
?
10.?如图,在平面直角坐标系中,点A的坐标为(4,0),直线l:y=-2x+4分别与x轴、y轴相交于B,C两点.
(1)点B的坐标为________,点C的坐标为________.
(2)在直线l上是否存在点P,使得△APO是以P为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
?
11.?将三角形纸片ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,AB=AC=4,BC=5,若以B′,F,C为顶点的三角形与△ABC相似,则CF=______.
?????
第11题图??????????????????第12题图
12.?如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在BC,CD上,若以M,N,C为顶点的三角形与△AED相似,则CM的长为_________.
13.?如图,在Rt△ABC中,AB=3?cm,AC=6?cm.动点M从点A出发沿AB方向以1?cm/s的速度向点B匀速运动;同时动点N从点C出发沿CA方向以2?cm/s的速度向点A匀速运动,当一个动点到达端点时,另一个动点随之停止运动.是否存在某一时刻t,使以A,M,N为顶点的三角形与△ABC相似?若存在,求出t的值;若不存在,请说明理由.
?
【参考答案】
??课前预习
1.?①证明略.
②△EDA∽△EAB,△DEA∽△DAC,△BAE∽△CDA.
③△AQP∽△PRB,△AQP∽△APB,△PBR∽△ABP.
??精讲精练
1.?4:1
2.?2或12?cm
3.?
4.?D
5.?
6.?
7.?(1)3;(2)12
8.?
9.?
10.?B
11.?(1)(,);(2)(,)
12.?
13.?作图略.
14.?或2
15.?或
16.?1,6或
【参考答案】
??复习巩固
1.?
2.?1或6
3.?(,)
4.?①②
5.?证明略.
6.?②④⑤⑥
7.?证明略.
8.?证明略.
9.?(1)证明略;
(2)证明略;
(3)AM⊥BE,理由略.
10.?(1)(2,0);(0,4);
(2)存在,P1(,),P2(,).
11.?或
12.?或
13.?存在,或,理由略.
??课前预习
1.?按要求解决下列问题:
①如图,AB⊥BD于点B,ED⊥BD于点D,点C是线段BD上一点,连接AC,CE,AC⊥CE.求证:△ABC∽△CDE.
?
②如图,将两个全等的等腰直角三角形如图摆放(顶点A重合),所有的点都在同一平面内.请找出图中的相似三角形(不包括全等).
?
③如图,已知A是等边三角形PQR的边RQ延长线上的点,B是QR延长线上的点.若∠APB=120°,请找出图中的相似三角形.
?
??知识点睛
1.?相似综合模型
一线三等角
图形
?
特征
三等角
结论
△ABC∽△CDE
旋转放缩
图形
?????????
特征
成比例线段共端点
结论
ABC∽△ADE或△ABD∽△ACE
△十字模型
图形
?????????
特征
矩形背景下,DE⊥CF(平行四边形背景下,∠B+∠EGC=180°)
结论
2.?“斜直角”特征——斜直角放正,得相似
?????
3.?“相似”与“∽”
“相似”与“∽”的区别在于两个三角形的对应关系是否确定.“相似”只能表示两个三角形的形状相同,但对应关系不确定;出现“相似”时,一般需要分类讨论.
??精讲精练
1.?如图,将矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的点F处,若DE=5,AB=8,则S△ABF:S△FCE=_____.
?
2.?如图,在四边形ABCD中,AD∥BC,AB=CD,AD=6?cm,BC=14?cm,∠B=60°.P为下底BC上一点(不与点B,C重合),连接AP,过点P作射线PE交线段DC于点E,使得
∠APE=∠B.若DE:EC=5:3,则BP=_________.
??
3.?如图,在正方形ABCD中,点E,F分别在BC,CD上,如果AE=3,EF=2,AF=,那么正方形ABCD的边长等于__________.
?
4.?如图,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=,则MF的长是(????)
A.?
B.
C.1?D.?
5.?如图,在△ABC中,D,E分别在边AB,AC上,且DE∥BC.将△DAE绕点A顺时针旋转若干角度,得到△AD′E′,连接BD′,CE′.若AC=3,AB=4,则_________.
?
6.?如图,在Rt△ABC中,∠ACB=90°,BC=9,AC=6,CD⊥AB于点D,点E是线段AC上一动点,连接DE,过点D作FD⊥ED,交线段BC于点F,连接EF.若EC=2,则EF=_____.
?
?如图,矩形ABCD中,AD=nAB,E,F,G,H分别是AB,BC,CD,AD边上的点,
EG⊥FH.
(1)当n=1,FH=3时,EG=___________;
(2)当n=2,FH=时,四边形EFGH的面积为_______.
?
8.?在矩形ABCD中,AB=4,BC=3,点P在线段AB上.若将
△DAP沿DP折叠,使点A落在矩形对角线AC上的A′处,则AP的长为_____________.
9.?矩形纸片ABCD中,AB=5,AD=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.若CB′为1,则AE的长为___________.
?
10.?如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为(????)
A.18?B.?C.?D.
??
11.?在平面直角坐标系中,将一含30°角的直角三角板放置在坐标系中.
(1)如图1,若该三角板直角顶点与原点O重合,顶点A的坐标为(-1,2),∠ABO=30°,顶点B在第一象限,则点B的坐标为_______.
(2)如图2,若该三角板直角顶点落在点C(2,2),顶点A的坐标为(3,0),∠ABC=30°,顶点B在第一象限,则点B的坐标为___________.
???
图1
??????????????????
????图2
12.?如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=,则BD的长为___________.
?
13.?在下图中,根据线段DE补全△DEF,使得△DEF与△ABC相似.(△DEF的顶点F在直线DE的上方)
?
?
14.?将三角形纸片ABC按如图1所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,则BF=___________.
?
图1
????????????????????备用图
?
15.?如图,在△ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止运动,设运动时间为t秒.当以B,D,E为顶点的三角形与△ABC相似时,则t的值为________.
?
16.?如图,在梯形ABCD中,AB∥CD,∠B=∠C=90°,点E在BC边上,AB=3,CD=2,BC=7.若△ABE与△ECD相似,则CE=___________.
?
相似模型(二)(习题)
??复习巩固
1.?如图,等腰Rt△ABC的直角边长为3,P为斜边BC上一点,且BP=,D为AC上一点.若∠APD=45°,则CD=______.
?
2.?如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=.点P在线段AB上,若△PCD是以点P为直角顶点的直角三角形,则AP=__________.
?
3.?如图,把矩形纸片OABC放入平面直角坐标系中,使OA,OC分别落在x轴、y轴上,连接AC,将纸片OABC沿AC折叠,使点B落在点D的位置.若点B的坐标为(2,4),则点D的坐标是__________.
?
4.?如图,在矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交CD于点F,连接AF.设,则给出下列结论:①△ABE∽△ECF;②AE平分∠BAF;③当k=1时,△ABE∽△ADF.其中正确的是_____________.
?
5.?如图,在矩形ABCD中,E,N,F,M分别是边AB,BC,CD,DA上的点,且EF⊥MN,求证:.
?
?
?
6.?如图,△ABC为等腰直角三角形,∠BAC=90°,BC=1,E为直角边AB上任意一点,以线段CE为斜边作等腰Rt△CDE,连接AD,有下列说法:①AC⊥DE;②∠BCE=∠ACD;
③△AED∽△ECB;④△AFE∽△DFC;⑤AD∥BC;⑥四边形ABCD面积的最大值为.其中正确的是__________.
?
7.?如图,D是Rt△ABC的斜边AB上一点,点E在AC上,连接DE,CD,且∠ADE=∠BCD,CF⊥CD交DE的延长线于点F,连接AF.求证:AF⊥AB.
?
8.?如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是AC上的点,若AF⊥BE,垂足为F.求证:∠BFD=∠C.
?
9.?
如图,在△ABC中,AB=AC,AD⊥BC,DE⊥AC,M为DE的中点,AM与BE相交于点N,AD与BE相交于点F.
求证:(1);
(2)△BCE∽△ADM;
(3)猜想AM与BE的位置关系,并说明理由.
?
10.?如图,在平面直角坐标系中,点A的坐标为(4,0),直线l:y=-2x+4分别与x轴、y轴相交于B,C两点.
(1)点B的坐标为________,点C的坐标为________.
(2)在直线l上是否存在点P,使得△APO是以P为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
?
11.?将三角形纸片ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,AB=AC=4,BC=5,若以B′,F,C为顶点的三角形与△ABC相似,则CF=______.
?????
第11题图??????????????????第12题图
12.?如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在BC,CD上,若以M,N,C为顶点的三角形与△AED相似,则CM的长为_________.
13.?如图,在Rt△ABC中,AB=3?cm,AC=6?cm.动点M从点A出发沿AB方向以1?cm/s的速度向点B匀速运动;同时动点N从点C出发沿CA方向以2?cm/s的速度向点A匀速运动,当一个动点到达端点时,另一个动点随之停止运动.是否存在某一时刻t,使以A,M,N为顶点的三角形与△ABC相似?若存在,求出t的值;若不存在,请说明理由.
?
【参考答案】
??课前预习
1.?①证明略.
②△EDA∽△EAB,△DEA∽△DAC,△BAE∽△CDA.
③△AQP∽△PRB,△AQP∽△APB,△PBR∽△ABP.
??精讲精练
1.?4:1
2.?2或12?cm
3.?
4.?D
5.?
6.?
7.?(1)3;(2)12
8.?
9.?
10.?B
11.?(1)(,);(2)(,)
12.?
13.?作图略.
14.?或2
15.?或
16.?1,6或
【参考答案】
??复习巩固
1.?
2.?1或6
3.?(,)
4.?①②
5.?证明略.
6.?②④⑤⑥
7.?证明略.
8.?证明略.
9.?(1)证明略;
(2)证明略;
(3)AM⊥BE,理由略.
10.?(1)(2,0);(0,4);
(2)存在,P1(,),P2(,).
11.?或
12.?或
13.?存在,或,理由略.
