人教版九年级数学下册 27.3 位似第1课时位似图形的概念及画法课件(共20张PPT)
文档属性
| 名称 | 人教版九年级数学下册 27.3 位似第1课时位似图形的概念及画法课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 568.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 14:59:49 | ||
图片预览






文档简介
第 二十七章 相 似
位 似
第1课时 位似图形的概念及画法
会画位似图形,能够根据位似比的大小把一个图形放大或缩小.(难点)
学 习 目 标
1
2
理解位似图形的概念,理解位似变化是特殊的相似变化. (重点)
图片引入
新课导入
在日常生活中,经常遇到一些把图形放大或缩小,但是图形的形状不改变的情形. 观察下面的图形,它们有哪些相似点?
知识讲解
★ 位似图形的概念
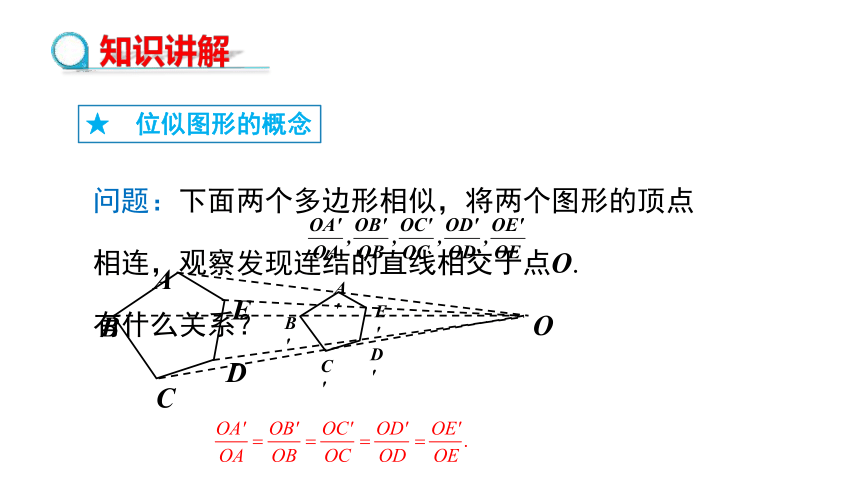
问题:下面两个多边形相似,将两个图形的顶点相连,观察发现连结的直线相交于点O. 有什么关系?
A
B
C
D
E
E'
D'
C'
B'
A'
O
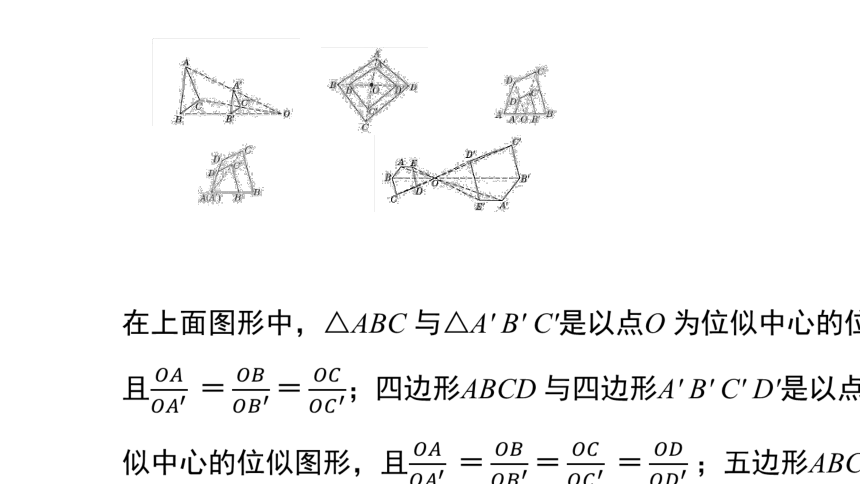
两个相似多边形,如果它们对应顶点所在的直线相交于一点,并且这点与对应顶点所连线段成比例,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.
归纳:
?
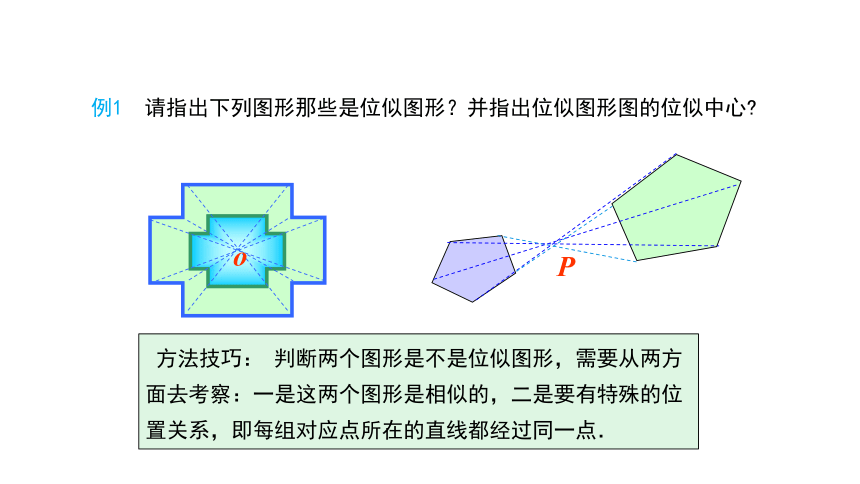
例1 请指出下列图形那些是位似图形?并指出位似图形图的位似中心?
o
P
方法技巧: 判断两个图形是不是位似图形,需要从两方面去考察:一是这两个图形是相似的,二是要有特殊的位置关系,即每组对应点所在的直线都经过同一点.
★ 位似图形的性质
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
归纳:
4. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.
1. 位似图形的对应角相等,对应边成比例,周长比等于相似比,面积比等于相似比的平方;
2. 位似图形的对应点的连线相交于一点,即经过位似中心;
3. 位似图形的对应边互相平行或在同一条直线上;
?
?
★ 位似图形的画法
例3 如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA、OB、OC;
在射线OA、OB、OC上分别取点D、E、F,使OD = 2OA,OE = 2OB,OF = 2OC;
顺次连结D、E、F,使△DEF与△ABC位似,相似比为2.
想一想:你还有其他的画法吗?
A
B
C
F
E
D
O
思考:上面点 O取在两个三角形的同侧,如果点 O在两个三角形之间呢?能不能画出这时的图形?
解:画射线OA、OB、OC;
沿着射线OA、OB、OC反方向上分别取点D、E、F,OD = 2OA,OE = 2OB,OF = 2OC;
顺次连结D、E、F,使△DEF与△ABC位似,相似比为2.
A
B
C
O
E
F
D
画位似图形的一般步骤:
归纳:
(1)确定位似中心;
(2)分别连接位似中心和能代表原图的关键点并延长;
(3)根据相似比,确定能代表所画的位似图形的关键点;
(4)按照原图的形状,顺次连接上述各点,得到放大或缩小后的图形.
随堂训练
两个位似图形中的对应角_ ___,对应线段___ __,对应顶点的连线必经过___ ____.
2.位似图形上某一对对应点到位似中心的距离分别为5和10,则它们的位似比为__ _.
相等
成比例
位似中心
1:2
?
1:16
4.已知边长为1的正方形ABCD,以它的两条对角线的交点为位似中心,画一个边长为2且与它位似的正方形.
A
B
C
D
E
H
G
F
O
解:画射线OA、OB、OC、OD;在射线OA、OB、OC、OD上分别取点D、E、F,使OE = 2OA , OF = 2OB , OG = 2OC , OH = 2OD;顺次连结E、F、G、H,使正方形ABCD与正方形EFGH位似,相位似比为1:
5.如图所示,四边形ABCD的一个位似图形是四边形A′ B′ C′ D′ ,且A,B,C,D的对应点分别是A′ ,B′ ,C′ ,D′. 图中给出了AB的对应边A′ B′所在的位置,请把四边形A′ B′ C′ D′其余部分补画上.
解:(1)连接AA′,BB′,相交于点O,则点O 为位似中心;
(2)作射线CO,DO ;
(3)分别过点A′,B′作A′ D′∥AD 交射线DO 于点D′,B′ C′∥ BC 交射线CO 于点C′ ;
(4)连接C′D′,四边形A′ B′ C′D′即为所要画的图形(如图 所示).
课堂小结
位似图形的概念
及画法
定义
性质
作位似图形:关键是确定位似中心、相似比和找关键点的对应点.
① 两个图形相似.
②对应点的连线相交于一点,对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
等于相似比.
画法
两个相似多边形,如果它们对应顶点所在的直线相交于一点,并且这点与对应顶点所连线段成比例,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.
再见
位 似
第1课时 位似图形的概念及画法
会画位似图形,能够根据位似比的大小把一个图形放大或缩小.(难点)
学 习 目 标
1
2
理解位似图形的概念,理解位似变化是特殊的相似变化. (重点)
图片引入
新课导入
在日常生活中,经常遇到一些把图形放大或缩小,但是图形的形状不改变的情形. 观察下面的图形,它们有哪些相似点?
知识讲解
★ 位似图形的概念
问题:下面两个多边形相似,将两个图形的顶点相连,观察发现连结的直线相交于点O. 有什么关系?
A
B
C
D
E
E'
D'
C'
B'
A'
O
两个相似多边形,如果它们对应顶点所在的直线相交于一点,并且这点与对应顶点所连线段成比例,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.
归纳:
?
例1 请指出下列图形那些是位似图形?并指出位似图形图的位似中心?
o
P
方法技巧: 判断两个图形是不是位似图形,需要从两方面去考察:一是这两个图形是相似的,二是要有特殊的位置关系,即每组对应点所在的直线都经过同一点.
★ 位似图形的性质
从左图中我们可以看到,△OAB∽△OA′B′,
则 ,AB∥A′B′. 右图呢?你得到了什么?
A
B
E
C
D
O
A′
B′
C′
D′
E′
A
B
C
O
A′
B′
C′
归纳:
4. 位似图形上任意一对对应点到位似中心的距离之比等于相似比.
1. 位似图形的对应角相等,对应边成比例,周长比等于相似比,面积比等于相似比的平方;
2. 位似图形的对应点的连线相交于一点,即经过位似中心;
3. 位似图形的对应边互相平行或在同一条直线上;
?
?
★ 位似图形的画法
例3 如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.
解:画射线OA、OB、OC;
在射线OA、OB、OC上分别取点D、E、F,使OD = 2OA,OE = 2OB,OF = 2OC;
顺次连结D、E、F,使△DEF与△ABC位似,相似比为2.
想一想:你还有其他的画法吗?
A
B
C
F
E
D
O
思考:上面点 O取在两个三角形的同侧,如果点 O在两个三角形之间呢?能不能画出这时的图形?
解:画射线OA、OB、OC;
沿着射线OA、OB、OC反方向上分别取点D、E、F,OD = 2OA,OE = 2OB,OF = 2OC;
顺次连结D、E、F,使△DEF与△ABC位似,相似比为2.
A
B
C
O
E
F
D
画位似图形的一般步骤:
归纳:
(1)确定位似中心;
(2)分别连接位似中心和能代表原图的关键点并延长;
(3)根据相似比,确定能代表所画的位似图形的关键点;
(4)按照原图的形状,顺次连接上述各点,得到放大或缩小后的图形.
随堂训练
两个位似图形中的对应角_ ___,对应线段___ __,对应顶点的连线必经过___ ____.
2.位似图形上某一对对应点到位似中心的距离分别为5和10,则它们的位似比为__ _.
相等
成比例
位似中心
1:2
?
1:16
4.已知边长为1的正方形ABCD,以它的两条对角线的交点为位似中心,画一个边长为2且与它位似的正方形.
A
B
C
D
E
H
G
F
O
解:画射线OA、OB、OC、OD;在射线OA、OB、OC、OD上分别取点D、E、F,使OE = 2OA , OF = 2OB , OG = 2OC , OH = 2OD;顺次连结E、F、G、H,使正方形ABCD与正方形EFGH位似,相位似比为1:
5.如图所示,四边形ABCD的一个位似图形是四边形A′ B′ C′ D′ ,且A,B,C,D的对应点分别是A′ ,B′ ,C′ ,D′. 图中给出了AB的对应边A′ B′所在的位置,请把四边形A′ B′ C′ D′其余部分补画上.
解:(1)连接AA′,BB′,相交于点O,则点O 为位似中心;
(2)作射线CO,DO ;
(3)分别过点A′,B′作A′ D′∥AD 交射线DO 于点D′,B′ C′∥ BC 交射线CO 于点C′ ;
(4)连接C′D′,四边形A′ B′ C′D′即为所要画的图形(如图 所示).
课堂小结
位似图形的概念
及画法
定义
性质
作位似图形:关键是确定位似中心、相似比和找关键点的对应点.
① 两个图形相似.
②对应点的连线相交于一点,对应边互相
平行或在同一直线上.
③任意一对对应点到位似中心的距离之比
等于相似比.
画法
两个相似多边形,如果它们对应顶点所在的直线相交于一点,并且这点与对应顶点所连线段成比例,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.
再见
