鲁科版(2019)高中物理 选择性必修第三册 第1章 拓展课 气体实验定律和理想气体状态方程的应用课件17 张PPT
文档属性
| 名称 | 鲁科版(2019)高中物理 选择性必修第三册 第1章 拓展课 气体实验定律和理想气体状态方程的应用课件17 张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-10 17:19:25 | ||
图片预览






文档简介
拓展课 气体实验定律和理想气体状态方程的应用
[要点归纳]
1.理想气体状态方程的推导
核心要点
理想气体状态方程
2.对理想气体状态方程的理解
(1)成立条件:一定质量的理想气体。
(2)该方程表示的是气体三个状态参量的关系,与中间的变化过程无关。
(3)公式中常量C仅由气体的种类和质量决定,与状态参量(p、V、T)无关。
(4)方程应用时各量的单位:温度T必须是热力学温度,公式两边中压强p和体积V单位必须统一,但不一定是国际单位制中的单位。
3.理想气体状态方程与气体实验定律
[经典示例]
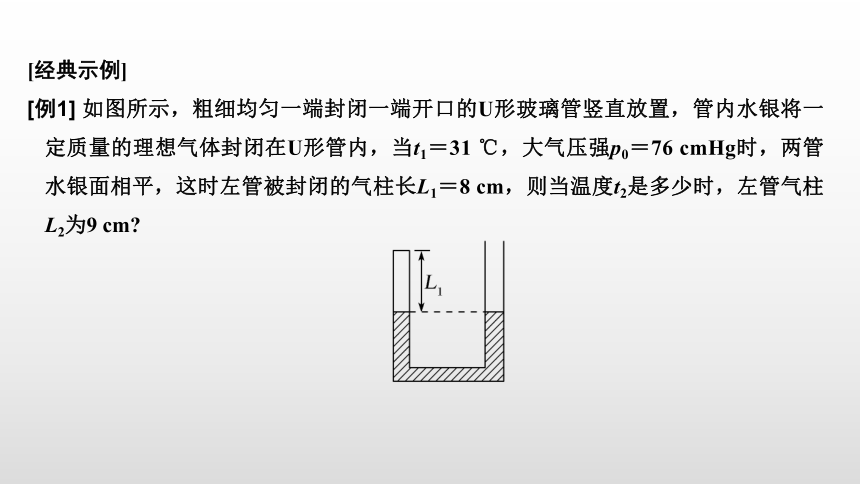
[例1] 如图所示,粗细均匀一端封闭一端开口的U形玻璃管竖直放置,管内水银将一定质量的理想气体封闭在U形管内,当t1=31 ℃,大气压强p0=76 cmHg时,两管水银面相平,这时左管被封闭的气柱长L1=8 cm,则当温度t2是多少时,左管气柱L2为9 cm?
解析 设玻璃管的横截面积为S,
初状态:p1=p0=76 cmHg,
V1=L1·S=8 cm·S,T1=304 K;
末状态:p2=p0+2 cmHg=78 cmHg,
V2=L2·S=9 cm·S,
代入数据解得:T2=351 K,则t2=(351-273) ℃=78 ℃。
答案 78 ℃
规律总结 理想气体状态方程的应用要点
(1)选对象:根据题意,选出所研究的某一部分气体,这部分气体在状态变化过程中,其质量必须保持一定。
(2)找参量:找出作为研究对象的这部分气体发生状态变化前后的一组p、V、T数值或表达式,压强的确定往往是个关键,常需结合力学知识(如力的平衡条件或牛顿运动定律)才能写出表达式。
(3)认过程:过程表示两个状态之间的一种变化式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定,认清变化过程是正确选用物理规律的前提。
(4)列方程:根据研究对象状态变化的具体方式,选用理想气体状态方程或某一实验定律,代入具体数值,T必须用热力学温度,p、V的单位要统一,最后分析讨论所得结果的合理性及其物理意义。
[针对训练1] 一定质量的理想气体,在某一平衡状态下的压强、体积和温度分别为p1、V1、T1,在另一平衡状态下的压强、体积和温度分别为p2、V2、T2,下列关系中可能正确的是( )
答案 D
[要点归纳]
核心要点
理想气体状态方程与气体图像问题
[经典示例]
[例2] 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
解析 从p-V图中可以直观地看出,气体在A、B、C、D各状态下压强和体积分别为pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,VA=10 L,VC=40 L,VD=20 L。
在V-T图上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
答案 (1)600 K 600 K 300 K (2)见解析
[针对训练2] 在下列图像中,不能反映一定质量的理想气体经历了等温变化→等容变化→等压变化后,又回到初始状态的图像是(A中曲线为双曲线的一支)( )
解析 根据p-V、p-T、V-T图像的物理意义可以判断,其中D反映的是理想气体经历了等温变化→等压变化→等容变化,与题意不符。
答案 D
[要点归纳]
1.理想气体状态方程的推导
核心要点
理想气体状态方程
2.对理想气体状态方程的理解
(1)成立条件:一定质量的理想气体。
(2)该方程表示的是气体三个状态参量的关系,与中间的变化过程无关。
(3)公式中常量C仅由气体的种类和质量决定,与状态参量(p、V、T)无关。
(4)方程应用时各量的单位:温度T必须是热力学温度,公式两边中压强p和体积V单位必须统一,但不一定是国际单位制中的单位。
3.理想气体状态方程与气体实验定律
[经典示例]
[例1] 如图所示,粗细均匀一端封闭一端开口的U形玻璃管竖直放置,管内水银将一定质量的理想气体封闭在U形管内,当t1=31 ℃,大气压强p0=76 cmHg时,两管水银面相平,这时左管被封闭的气柱长L1=8 cm,则当温度t2是多少时,左管气柱L2为9 cm?
解析 设玻璃管的横截面积为S,
初状态:p1=p0=76 cmHg,
V1=L1·S=8 cm·S,T1=304 K;
末状态:p2=p0+2 cmHg=78 cmHg,
V2=L2·S=9 cm·S,
代入数据解得:T2=351 K,则t2=(351-273) ℃=78 ℃。
答案 78 ℃
规律总结 理想气体状态方程的应用要点
(1)选对象:根据题意,选出所研究的某一部分气体,这部分气体在状态变化过程中,其质量必须保持一定。
(2)找参量:找出作为研究对象的这部分气体发生状态变化前后的一组p、V、T数值或表达式,压强的确定往往是个关键,常需结合力学知识(如力的平衡条件或牛顿运动定律)才能写出表达式。
(3)认过程:过程表示两个状态之间的一种变化式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定,认清变化过程是正确选用物理规律的前提。
(4)列方程:根据研究对象状态变化的具体方式,选用理想气体状态方程或某一实验定律,代入具体数值,T必须用热力学温度,p、V的单位要统一,最后分析讨论所得结果的合理性及其物理意义。
[针对训练1] 一定质量的理想气体,在某一平衡状态下的压强、体积和温度分别为p1、V1、T1,在另一平衡状态下的压强、体积和温度分别为p2、V2、T2,下列关系中可能正确的是( )
答案 D
[要点归纳]
核心要点
理想气体状态方程与气体图像问题
[经典示例]
[例2] 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
解析 从p-V图中可以直观地看出,气体在A、B、C、D各状态下压强和体积分别为pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,VA=10 L,VC=40 L,VD=20 L。
在V-T图上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
答案 (1)600 K 600 K 300 K (2)见解析
[针对训练2] 在下列图像中,不能反映一定质量的理想气体经历了等温变化→等容变化→等压变化后,又回到初始状态的图像是(A中曲线为双曲线的一支)( )
解析 根据p-V、p-T、V-T图像的物理意义可以判断,其中D反映的是理想气体经历了等温变化→等压变化→等容变化,与题意不符。
答案 D
同课章节目录
- 第1章 分子动理论与气体实验定律
- 第1节 分子动理论的基本观点
- 第2节 科学测量:用油膜法估测油酸分子的大小
- 第3节 气体分子速率分布的统计规律
- 第4节 科学探究:气体压强与体积的关系
- 第5节 气体实验定律
- 第2章 固体与液体
- 第1节 固体类型及微观结构
- 第2节 表面张力和毛细现象
- 第3节 材料及其应用
- 第3章 热力学定律
- 第1节 热力学第一定律
- 第2节 能量的转化与守恒
- 第3节 热力学第二定律
- 第4节 熵——系统无序程度的量度
- 第4章 原子结构
- 第1节 电子的发现与汤姆孙原子模型
- 第2节 原子的核式结构模型
- 第3节 光谱与氢原子光谱
- 第4节 玻尔原子模型
- 第5章 原子核与核能
- 第1节 认识原子核
- 第2节 原子核衰变及半衰期
- 第3节 核力与核能
- 第4节 核裂变和核聚变
- 第5节 核能的利用与环境保护
- 第6章 波粒二象性
- 第1节 光电效应及其解释
- 第2节 实物粒子的波粒二象性
