人教版(2019)高中物理 选择性必修第三册 第2章 拓展课 气体实验定律和理想气体状态方程的应用课件 34 张PPT
文档属性
| 名称 | 人教版(2019)高中物理 选择性必修第三册 第2章 拓展课 气体实验定律和理想气体状态方程的应用课件 34 张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览











文档简介
拓展课 气体实验定律和理想气体状态方程的应用
核心
素养
物理观念
科学思维
1.进一步熟练掌握气体实验三定律和理想气体状态方程,并能熟练应用。
2.会巧妙地选择研究对象,使变质量气体问题转化为定质量的气体问题。
3.会利用图像对气体状态及状态变化进行分析,并能解决不同图像之间的转换。
体会用气体规律处理实际气体问题的方法和步骤。
[要点归纳]
分析变质量问题时,可以通过巧妙选择合适的研究对象,使这类问题转化为定质量的气体问题,用理想气体状态方程求解。
核心要点
变质量气体问题
1.打气问题
向球、轮胎中充气是一个典型的气体变质量的问题。只要选择球内原有气体和即将打入的气体作为研究对象,就可以把充气过程中的气体质量变化的问题转化为定质量气体的状态变化问题。
2.抽气问题
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,总质量不变,故抽气过程可看做是等温膨胀过程。
[试题案例]
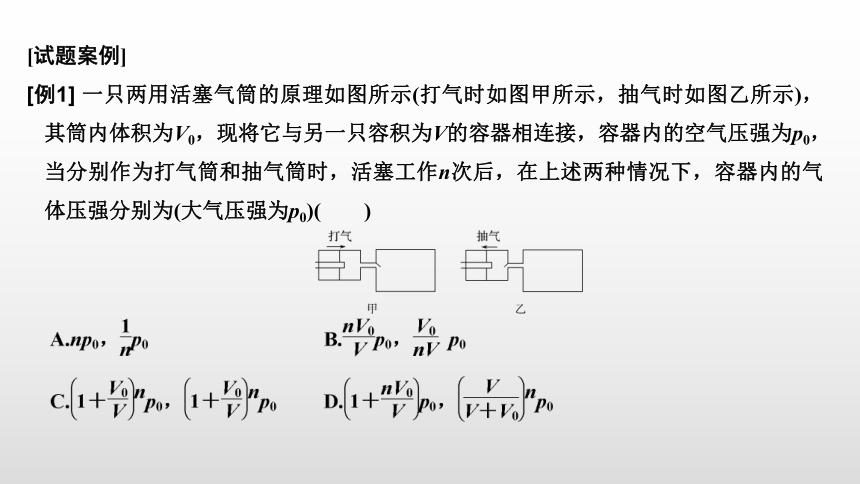
[例1] 一只两用活塞气筒的原理如图所示(打气时如图甲所示,抽气时如图乙所示),其筒内体积为V0,现将它与另一只容积为V的容器相连接,容器内的空气压强为p0,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为(大气压强为p0)( )
解析 打气时,活塞每推动一次,就把体积为V0、压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0、体积为nV0的气体压入容器内,容器内原来有压强为p0、体积为V的气体,根据玻意耳定律得:
p0(V+nV0)=p′V。
答案 D
答案 40 g
[要点归纳]
此类问题的特点是:用液柱或活塞隔开两部分气体,当气体的状态参量p、V、T都发生变化时,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解。假设法的一般思路为
(1)假设液柱或活塞不发生移动,两部分气体均做等容变化。
核心要点
判断液柱(或活塞)的移动问题
[试题案例]
[例2] 如图所示,两端封闭、粗细均匀、竖直放置的玻璃管内,有一长为h的水银柱,将管内气体分为两部分,已知l2=2l1。若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)
解析 水银柱原来处于平衡状态,所受合外力为零,即此时两部分气体的压强差Δp=p1-p2=ph。温度升高后,两部分气体的压强都增大,若Δp1>Δp2,水银柱所受合外力方向向上,应向上移动;若Δp1<Δp2,水银柱向下移动;若Δp1=Δp2,水银柱不动。所以判断水银柱怎样移动,就是分析其合力方向,即判断两部分气体的压强哪一个增大得多。
(1)假设法
假设水银柱不动,两部分气体都做等容变化,分别对两部分气体应用查理定律:
又因为ΔT2=ΔT1,T1=T2,p1=p2+ph>p2,
所以Δp1>Δp2,即水银柱上移。
(2)图像法
在同一p-T图上画出两段气柱的等容线,如图所示,因为在温度相同时,p1>p2,得气柱l1等容线的斜率较大,当两气柱升高相同的温度ΔT时,其压强的增量Δp1>Δp2。所以水银柱上移。
(3)极限法
由于p2较小,设想p2=0,即上部为真空,升温则p1增大,水银柱上移,降温则水银柱下降。
答案 水银柱上移
方法凝炼 液柱(或活塞)移动问题的其他分析方法
(1)极限法
所谓极限法就是将问题推向极端。如在讨论压强大小变化时,将变化较大的压强推向无穷大,而将变化较小的压强推向零。这样使复杂的问题变得简单明了。
(2)图像法
利用p-T图像:先在p-T图线上画出两气体的等容图线,找到它们因温度发生变化而引起的压强变化量Δp,比较两者的Δp或结合受力分析比较ΔpS从而得出结论。
[针对训练2] (多选)如图,竖直放置的均匀等臂U形导热玻璃管两端封闭,管内水银封有A、B两段气柱,左管水银面高于右管水银面,高度差为h,稳定时A、B气柱的压强分别为pA和pB,则( )
答案 BC
[要点归纳]
1.理想气体状态变化的过程,可以用不同的图像描述。已知某个图像,可以根据这一图像转换成另一图像,如由p-V图象变成p-T图像或V-T图像。
2.在图像转换问题中要特别注意分析隐含物理量。p-V图像中重点比较气体的温度,p-T图像中重点比较气体的体积,以及V-T图像中重点比较气体的压强。确定了图像中隐含物理量的变化,图像转换问题就会迎刃而解。
核心要点
气体图像之间的转换
[试题案例]
[例3] 一定质量的理想气体由状态A变为状态D,其有关数据如图甲所示。若状态D的压强是2×104 Pa。
(1)求状态A的压强;
(2)请在乙图中画出该状态变化过程的p-T图像,并分别标出A、B、C、D各个状态,不要求写出计算过程。
解析 (1)A状态:pA=? VA=1 m3,TA=200 K
D状态:pD=2×104 Pa,VD=4 m3,TD=400 K
根据理想气体状态方程
(2)A到B做等容变化,等容线在p-T图像中为过原点的直线,B到C做等温变化,由甲图AC连线为过原点的直线,则C的压强与A压强相等,C到D做等容变化。
故图线为
答案 (1)4×104 Pa (2)见解析图
方法凝炼 一般状态变化图像的处理方法
基本方法:化“一般”为“特殊”。
如图是一定质量的某种气体的状态变化过程A→B→C→A。在V-T图线上,等压线是一簇延长线过原点的直线,过A、B、C三点作三条等压线分别表示三个等压过程,pA′[针对训练3] 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程中图乙中画成用体积V和温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
解析 (1)从p-V图中可以直观地看出,气体在A、B、C、D各状态下压强和体积分别为pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,VA=10 L,VC=40 L,VD=20 L。
由题意知B到C是等温变化,
所以TB=TC=600 K。
在V-T图上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
答案 (1)600 K 600 K 300 K (2)见解析
[要点归纳]
这类问题涉及两部分气体,它们之间虽然没有气体交换,但其压强或体积这些量间有一定的关系,分析清楚这些关系是解决问题的关键,解决这类问题的一般方法:
(1)分别选取每部分气体为研究对象,确定初、末状态参量,根据状态方程列式求解。
(2)认真分析两部分气体的压强、体积之间的关系,并列出方程。
(3)多个方程联立求解。
核心要点
相关联的两部分气体问题
[试题案例]
[例4] 用销钉固定的活塞把容器分成A、B两部分,其容积之比VA∶VB=2∶1,如图所示,起初A中有温度为127 ℃、压强为1.8×105 Pa的空气,B中有温度为27 ℃、压强为1.2×105 Pa的空气,拔去销钉,使活塞可以无摩擦地移动且不漏气,由于容器壁缓慢导热,最后两部分空气都变成室温27 ℃,活塞也停住,求最后A、B中气体的压强。
解析 对A空气,初状态:pA=1.8×105 Pa,VA=?,TA=400 K。
末状态:pA′=?,VA′=?,TA′=300 K,
对B空气,初状态:pB=1.2×105 Pa,VB=?TB=300 K。
末状态:pB′=?,VB′=?,TB′=300 K。
又VA+VB=VA′+VB′,VA∶VB=2∶1,pA′=pB′,
联立以上各式得pA′=pB′=1.3×105 Pa。
答案 都为1.3×105 Pa
[针对训练4] 光滑绝热的活塞把密封的圆筒容器分成A、B两部分,这两部分充有温度相同的气体,平衡时VA∶VB=1∶2,现将A中气体加热到127 ℃,B中气体降低到27 ℃,待重新平衡后,这两部分气体体积的比VA′∶VB′为( )
A.1∶1 B.2∶3
C.3∶4 D.2∶1
答案 B
因为pA=pB,pA′=pB′,TA=TB,
核心
素养
物理观念
科学思维
1.进一步熟练掌握气体实验三定律和理想气体状态方程,并能熟练应用。
2.会巧妙地选择研究对象,使变质量气体问题转化为定质量的气体问题。
3.会利用图像对气体状态及状态变化进行分析,并能解决不同图像之间的转换。
体会用气体规律处理实际气体问题的方法和步骤。
[要点归纳]
分析变质量问题时,可以通过巧妙选择合适的研究对象,使这类问题转化为定质量的气体问题,用理想气体状态方程求解。
核心要点
变质量气体问题
1.打气问题
向球、轮胎中充气是一个典型的气体变质量的问题。只要选择球内原有气体和即将打入的气体作为研究对象,就可以把充气过程中的气体质量变化的问题转化为定质量气体的状态变化问题。
2.抽气问题
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,总质量不变,故抽气过程可看做是等温膨胀过程。
[试题案例]
[例1] 一只两用活塞气筒的原理如图所示(打气时如图甲所示,抽气时如图乙所示),其筒内体积为V0,现将它与另一只容积为V的容器相连接,容器内的空气压强为p0,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为(大气压强为p0)( )
解析 打气时,活塞每推动一次,就把体积为V0、压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0、体积为nV0的气体压入容器内,容器内原来有压强为p0、体积为V的气体,根据玻意耳定律得:
p0(V+nV0)=p′V。
答案 D
答案 40 g
[要点归纳]
此类问题的特点是:用液柱或活塞隔开两部分气体,当气体的状态参量p、V、T都发生变化时,直接判断液柱或活塞的移动方向比较困难,通常先进行气体状态的假设,然后应用查理定律可以简单地求解。假设法的一般思路为
(1)假设液柱或活塞不发生移动,两部分气体均做等容变化。
核心要点
判断液柱(或活塞)的移动问题
[试题案例]
[例2] 如图所示,两端封闭、粗细均匀、竖直放置的玻璃管内,有一长为h的水银柱,将管内气体分为两部分,已知l2=2l1。若使两部分气体同时升高相同的温度,管内水银柱将如何运动?(设原来温度相同)
解析 水银柱原来处于平衡状态,所受合外力为零,即此时两部分气体的压强差Δp=p1-p2=ph。温度升高后,两部分气体的压强都增大,若Δp1>Δp2,水银柱所受合外力方向向上,应向上移动;若Δp1<Δp2,水银柱向下移动;若Δp1=Δp2,水银柱不动。所以判断水银柱怎样移动,就是分析其合力方向,即判断两部分气体的压强哪一个增大得多。
(1)假设法
假设水银柱不动,两部分气体都做等容变化,分别对两部分气体应用查理定律:
又因为ΔT2=ΔT1,T1=T2,p1=p2+ph>p2,
所以Δp1>Δp2,即水银柱上移。
(2)图像法
在同一p-T图上画出两段气柱的等容线,如图所示,因为在温度相同时,p1>p2,得气柱l1等容线的斜率较大,当两气柱升高相同的温度ΔT时,其压强的增量Δp1>Δp2。所以水银柱上移。
(3)极限法
由于p2较小,设想p2=0,即上部为真空,升温则p1增大,水银柱上移,降温则水银柱下降。
答案 水银柱上移
方法凝炼 液柱(或活塞)移动问题的其他分析方法
(1)极限法
所谓极限法就是将问题推向极端。如在讨论压强大小变化时,将变化较大的压强推向无穷大,而将变化较小的压强推向零。这样使复杂的问题变得简单明了。
(2)图像法
利用p-T图像:先在p-T图线上画出两气体的等容图线,找到它们因温度发生变化而引起的压强变化量Δp,比较两者的Δp或结合受力分析比较ΔpS从而得出结论。
[针对训练2] (多选)如图,竖直放置的均匀等臂U形导热玻璃管两端封闭,管内水银封有A、B两段气柱,左管水银面高于右管水银面,高度差为h,稳定时A、B气柱的压强分别为pA和pB,则( )
答案 BC
[要点归纳]
1.理想气体状态变化的过程,可以用不同的图像描述。已知某个图像,可以根据这一图像转换成另一图像,如由p-V图象变成p-T图像或V-T图像。
2.在图像转换问题中要特别注意分析隐含物理量。p-V图像中重点比较气体的温度,p-T图像中重点比较气体的体积,以及V-T图像中重点比较气体的压强。确定了图像中隐含物理量的变化,图像转换问题就会迎刃而解。
核心要点
气体图像之间的转换
[试题案例]
[例3] 一定质量的理想气体由状态A变为状态D,其有关数据如图甲所示。若状态D的压强是2×104 Pa。
(1)求状态A的压强;
(2)请在乙图中画出该状态变化过程的p-T图像,并分别标出A、B、C、D各个状态,不要求写出计算过程。
解析 (1)A状态:pA=? VA=1 m3,TA=200 K
D状态:pD=2×104 Pa,VD=4 m3,TD=400 K
根据理想气体状态方程
(2)A到B做等容变化,等容线在p-T图像中为过原点的直线,B到C做等温变化,由甲图AC连线为过原点的直线,则C的压强与A压强相等,C到D做等容变化。
故图线为
答案 (1)4×104 Pa (2)见解析图
方法凝炼 一般状态变化图像的处理方法
基本方法:化“一般”为“特殊”。
如图是一定质量的某种气体的状态变化过程A→B→C→A。在V-T图线上,等压线是一簇延长线过原点的直线,过A、B、C三点作三条等压线分别表示三个等压过程,pA′
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程中图乙中画成用体积V和温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
解析 (1)从p-V图中可以直观地看出,气体在A、B、C、D各状态下压强和体积分别为pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,VA=10 L,VC=40 L,VD=20 L。
由题意知B到C是等温变化,
所以TB=TC=600 K。
在V-T图上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
答案 (1)600 K 600 K 300 K (2)见解析
[要点归纳]
这类问题涉及两部分气体,它们之间虽然没有气体交换,但其压强或体积这些量间有一定的关系,分析清楚这些关系是解决问题的关键,解决这类问题的一般方法:
(1)分别选取每部分气体为研究对象,确定初、末状态参量,根据状态方程列式求解。
(2)认真分析两部分气体的压强、体积之间的关系,并列出方程。
(3)多个方程联立求解。
核心要点
相关联的两部分气体问题
[试题案例]
[例4] 用销钉固定的活塞把容器分成A、B两部分,其容积之比VA∶VB=2∶1,如图所示,起初A中有温度为127 ℃、压强为1.8×105 Pa的空气,B中有温度为27 ℃、压强为1.2×105 Pa的空气,拔去销钉,使活塞可以无摩擦地移动且不漏气,由于容器壁缓慢导热,最后两部分空气都变成室温27 ℃,活塞也停住,求最后A、B中气体的压强。
解析 对A空气,初状态:pA=1.8×105 Pa,VA=?,TA=400 K。
末状态:pA′=?,VA′=?,TA′=300 K,
对B空气,初状态:pB=1.2×105 Pa,VB=?TB=300 K。
末状态:pB′=?,VB′=?,TB′=300 K。
又VA+VB=VA′+VB′,VA∶VB=2∶1,pA′=pB′,
联立以上各式得pA′=pB′=1.3×105 Pa。
答案 都为1.3×105 Pa
[针对训练4] 光滑绝热的活塞把密封的圆筒容器分成A、B两部分,这两部分充有温度相同的气体,平衡时VA∶VB=1∶2,现将A中气体加热到127 ℃,B中气体降低到27 ℃,待重新平衡后,这两部分气体体积的比VA′∶VB′为( )
A.1∶1 B.2∶3
C.3∶4 D.2∶1
答案 B
因为pA=pB,pA′=pB′,TA=TB,
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
