人教版七年级上册数学 4.3.3余角和补角 同步练习(word含解析)
文档属性
| 名称 | 人教版七年级上册数学 4.3.3余角和补角 同步练习(word含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 65.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览



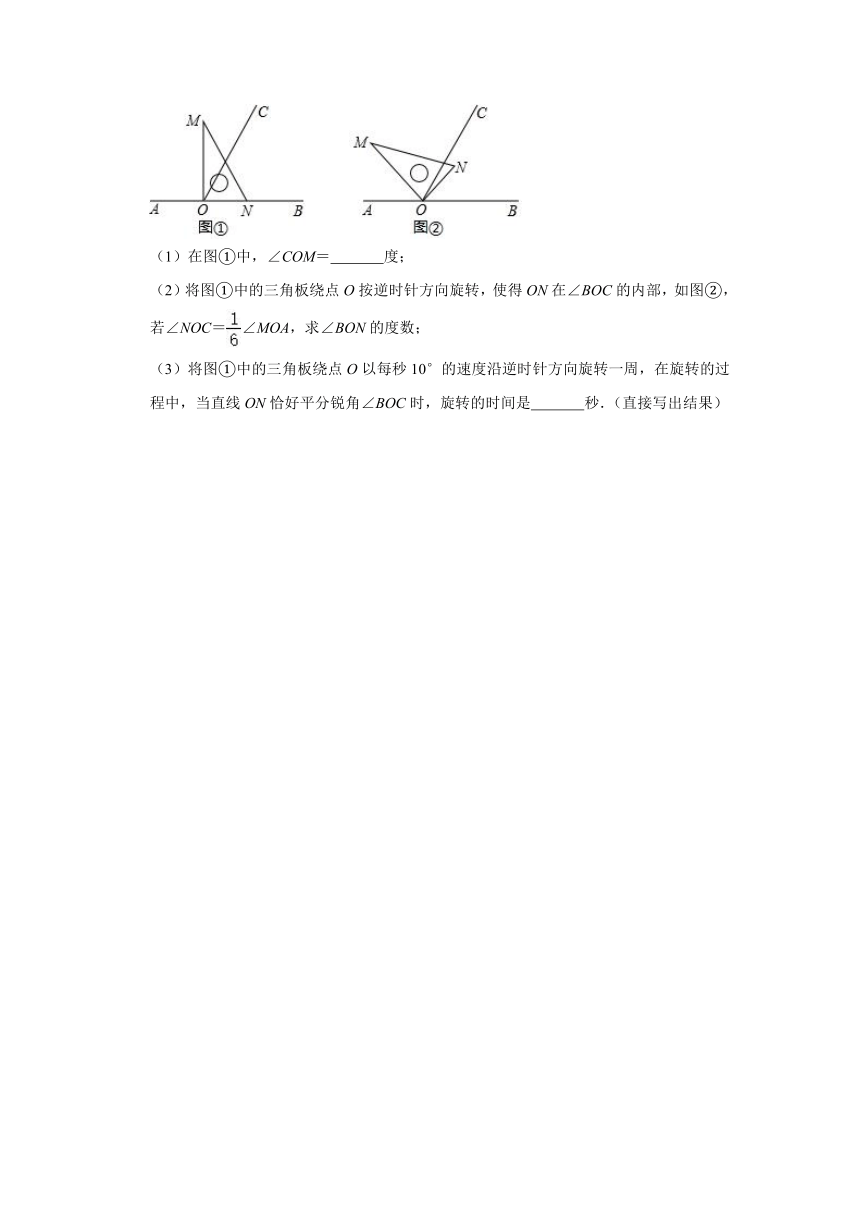
文档简介
4.3.3余角和补角
同步练习
一.选择题
1.若∠A与∠B互为补角,∠A=40°,则∠B=( )
A.50°
B.40°
C.140°
D.60°
2.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
3.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43°
B.34°
C.56°
D.50°
4.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
5.已知锐角α,那么∠α的补角与∠α的余角的差是( )
A.90°
B.120°
C.60°+α
D.180°﹣α
6.若α=27°25',则α的余角等于( )
A.62°25'
B.62°35'
C.152°25'
D.152°35'
7.如果∠1与∠2互补,∠2与∠3互余,那么∠1与∠3的关系是( )
A.∠1=90°+∠3
B.∠3=90°+∠1
C.∠1=∠3
D.∠1=180°﹣∠3
8.如图,∠AOC和∠BOD都是直角.如果∠DOC=58°,则下列判断错误的是( )
A.∠AOD=∠BOC
B.∠AOB=132°
C.∠AOB+∠DOC=180°
D.若∠DOC变小,则∠AOB变大
9.将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )
A.
B.
C.
D.
10.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对
B.4对
C.3对
D.2对
二.填空题
11.若两个角互补,且度数之比为3:2,求较大角度数为
.
12.一个角的补角与它的余角的3倍的差是40°,则这个角为
.
13.已知:如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,图形中相等的角有
对,互余的角有
对.
14.若一个角的补角与这个角的余角之和为200°,则这个角的度数为
度.
15.如图,将一副三角尺的直角顶点O重合在一起.若∠COB与∠DOA的比是5:13,OE平分∠DOA,则∠EOC=
度.
三.解答题
16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD和∠AOC互余,并求∠COD的度数.
17.如图,在直线AD上任取一点O,过点O做射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,求∠BOE的度数.
18.如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=60°,将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方.
(1)在图①中,∠COM=
度;
(2)将图①中的三角板绕点O按逆时针方向旋转,使得ON在∠BOC的内部,如图②,若∠NOC=∠MOA,求∠BON的度数;
(3)将图①中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON恰好平分锐角∠BOC时,旋转的时间是
秒.(直接写出结果)
参考答案
一.选择题
1.解:∵∠A与∠B互为补角,
∴∠A+∠B=180°,
∵∠A=40°,
∴∠B=180°﹣40°=140°.
故选:C.
2.解:A.一个锐角与一个钝角不一定互为补角,故本选项错误;
B.每一个锐角都有余角,故本选项正确;
C.只有两个锐角的和为90°时,这两个角才互余,故原说法错误;
D.钝角的没有余角,故此选项错误;
故选:B.
3.解:∠AOB=∠COD=90°,∠AOD=146°
则∠BOC=360°﹣2×90°﹣146°=34°
则∠BOC=34°.
故选:B.
4.解:①已知∠A=40°,则∠A的余角是50°,原说法正确;
②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;
④一个角的补角不一定是钝角,原说法错误.
说法正确的是①②,
故选:A.
5.解:(180°﹣∠α)﹣(90°﹣∠α)
=180°﹣∠α﹣90°+∠α
=90°.
故选:A.
6.解:α的余角=90°﹣α=90°﹣27°25'=62°35'.
故选:B.
7.解:∵∠1+∠2=180°
∴∠1=180°﹣∠2
又∵∠2+∠3=90°
∴∠3=90°﹣∠2
∴∠1﹣∠3=90°,即∠1=90°+∠3.
故选:A.
8.解:A、∵∠AOC和∠BOD都是直角,
∴∠AOD+∠DOC=∠DOC+∠BOC=90°,
∴∠AOD=∠BOC,故A正确,不符合题意;
B、∵∠DOC=58°,
∴∠AOD=32°,
∴∠AOB=32°+90°=122°,故B错误,符合题意,
C、∵∠AOD+∠DOC=∠DOC+∠BOC=90°,
∴∠AOD+∠DOC+∠DOC+∠BOC=180°,
∴∠AOB+∠DOC=180°,故C正确,不符合题意;
D、∵∠AOD+∠DOC+∠DOC+∠BOC=180°,
∴∠AOB+∠DOC=180°,
∴∠DOC变小,则∠AOB变大,故D正确,不符合题意.
故选:B.
9.解:A、∠1与∠2不互余,故本选项错误;
B、∠1与∠2不互余,故本选项错误;
C、∠1与∠2不互余,故本选项错误;
D、∠1与∠2互余,故本选项正确.
故选:D.
10.解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠1=∠AOC,
∠2=∠BOD,
∠AOE=∠COD,
∠BOE=∠COD,
∴图中相等的角有5对.
故选:A.
二.填空题
11.解:因为两个角的度数之比为3:2,
所以设这两个角的度数分别为(3x)°和(2x)°.
根据题意,列方程,得3x+2x=180,
解这个方程,得x=36,
所以3x=108.
即较大角度数为108°.
故答案为108°.
12.解:设这个角为x°,则其余角为(90﹣x)°,补角为(180﹣x)°,依题意有
180﹣x﹣3(90﹣x)=40,
解得x=65.
故这个角是65°.
故答案为:65°.
13.解:图形中相等的角有∠A=∠BCD,∠B=∠ACD,∠ACB=∠BDC,∠ACB=∠CDA,∠BDC=∠CDA,一共5对,互余的角有∠A和∠B,∠A和∠ACD,∠B和∠BCD,∠ACD和∠BCD,一共4对.
故答案为:5;4.
14.解:设这个角为x°,由题意得:
90﹣x+180﹣x=200,
解得:x=35,
故答案为:35.
15.解:∵∠COB+∠DOA=∠COB+∠COA+∠COB+∠DOB=∠AOB+∠COD=180°,
又∵∠COB与∠DOA的比是5:13,
∴∠DOA=180°×=130°,
∵OE平分∠DOA,
∴∠DOE=65°,
∴∠EOC=25°.
故答案为:25.
三.解答题
16.解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.
∵∠AOB=128°,OC平分∠AOB,
∴∠AOC=∠AOB=64°,
∵∠COD和∠AOC互余,
∴∠COD=90°﹣∠AOC=26°.
17.解:∵OC平分∠AOB,∠BOC=26°,
∴∠AOB=2∠BOC=52°.
∴∠BOD=180°﹣52°=128°.
∵OE平分∠DOB,
∴∠BOE=∠DOB=×128°=64°.
18.解:(1)∵将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方,
∴∠MON=90°,
∴∠COM=∠MON﹣∠BOC=90°﹣60°=30°,
故答案为:30
(2)设∠NOC=x,那么∠MOA=6x,∠BON=60°﹣x.
由题意,可知6x+90°+60°﹣x=180°,
即5x=180°﹣90°﹣60°,
即5x=30°,
所以x=6°.
所以∠BON=60°﹣x=60°﹣6°=54°.
(3)∵直线ON平分∠BOC,∠BOC=60°,
∴∠BON=30°或∠BON=210°,
∵三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,
∴直线ON平分∠BOC时,旋转的时间是3或21秒,
故答案为:3或21
同步练习
一.选择题
1.若∠A与∠B互为补角,∠A=40°,则∠B=( )
A.50°
B.40°
C.140°
D.60°
2.下列叙述正确的是( )
A.一个钝角和一个锐角一定互为补角
B.每一个锐角都有余角
C.两个锐角一定互为余角
D.一个钝角的余角是锐角
3.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC的度数为( )
A.43°
B.34°
C.56°
D.50°
4.下列说法中,正确的是( )
①已知∠A=40°,则∠A的余角是50°.
②若∠1+∠2=90°,则∠1和∠2互为余角.
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3互为补角.
④一个角的补角必为钝角.
A.①,②
B.①,②,③
C.③,④,②
D.③,④
5.已知锐角α,那么∠α的补角与∠α的余角的差是( )
A.90°
B.120°
C.60°+α
D.180°﹣α
6.若α=27°25',则α的余角等于( )
A.62°25'
B.62°35'
C.152°25'
D.152°35'
7.如果∠1与∠2互补,∠2与∠3互余,那么∠1与∠3的关系是( )
A.∠1=90°+∠3
B.∠3=90°+∠1
C.∠1=∠3
D.∠1=180°﹣∠3
8.如图,∠AOC和∠BOD都是直角.如果∠DOC=58°,则下列判断错误的是( )
A.∠AOD=∠BOC
B.∠AOB=132°
C.∠AOB+∠DOC=180°
D.若∠DOC变小,则∠AOB变大
9.将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )
A.
B.
C.
D.
10.如图,点A,O,B在一条直线上,OE⊥AB于点O,如果∠1与∠2互余,那么图中相等的角有( )
A.5对
B.4对
C.3对
D.2对
二.填空题
11.若两个角互补,且度数之比为3:2,求较大角度数为
.
12.一个角的补角与它的余角的3倍的差是40°,则这个角为
.
13.已知:如图,在△ABC中,∠ACB=90°,CD⊥AD,垂足为点D,图形中相等的角有
对,互余的角有
对.
14.若一个角的补角与这个角的余角之和为200°,则这个角的度数为
度.
15.如图,将一副三角尺的直角顶点O重合在一起.若∠COB与∠DOA的比是5:13,OE平分∠DOA,则∠EOC=
度.
三.解答题
16.如图,已知∠AOB=128°,OC平分∠AOB,请你在∠COB内部画射线OD,使∠COD和∠AOC互余,并求∠COD的度数.
17.如图,在直线AD上任取一点O,过点O做射线OB,OE平分∠DOB,OC平分∠AOB,∠BOC=26°时,求∠BOE的度数.
18.如图①,点O为直线AB上一点,过点O作射线OC,使∠BOC=60°,将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方.
(1)在图①中,∠COM=
度;
(2)将图①中的三角板绕点O按逆时针方向旋转,使得ON在∠BOC的内部,如图②,若∠NOC=∠MOA,求∠BON的度数;
(3)将图①中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,当直线ON恰好平分锐角∠BOC时,旋转的时间是
秒.(直接写出结果)
参考答案
一.选择题
1.解:∵∠A与∠B互为补角,
∴∠A+∠B=180°,
∵∠A=40°,
∴∠B=180°﹣40°=140°.
故选:C.
2.解:A.一个锐角与一个钝角不一定互为补角,故本选项错误;
B.每一个锐角都有余角,故本选项正确;
C.只有两个锐角的和为90°时,这两个角才互余,故原说法错误;
D.钝角的没有余角,故此选项错误;
故选:B.
3.解:∠AOB=∠COD=90°,∠AOD=146°
则∠BOC=360°﹣2×90°﹣146°=34°
则∠BOC=34°.
故选:B.
4.解:①已知∠A=40°,则∠A的余角是50°,原说法正确;
②若∠1+∠2=90°,则∠1和∠2互为余角,原说法正确;
③若∠1+∠2+∠3=180°,则∠1、∠2和∠3不能互为补角,原说法错误;
④一个角的补角不一定是钝角,原说法错误.
说法正确的是①②,
故选:A.
5.解:(180°﹣∠α)﹣(90°﹣∠α)
=180°﹣∠α﹣90°+∠α
=90°.
故选:A.
6.解:α的余角=90°﹣α=90°﹣27°25'=62°35'.
故选:B.
7.解:∵∠1+∠2=180°
∴∠1=180°﹣∠2
又∵∠2+∠3=90°
∴∠3=90°﹣∠2
∴∠1﹣∠3=90°,即∠1=90°+∠3.
故选:A.
8.解:A、∵∠AOC和∠BOD都是直角,
∴∠AOD+∠DOC=∠DOC+∠BOC=90°,
∴∠AOD=∠BOC,故A正确,不符合题意;
B、∵∠DOC=58°,
∴∠AOD=32°,
∴∠AOB=32°+90°=122°,故B错误,符合题意,
C、∵∠AOD+∠DOC=∠DOC+∠BOC=90°,
∴∠AOD+∠DOC+∠DOC+∠BOC=180°,
∴∠AOB+∠DOC=180°,故C正确,不符合题意;
D、∵∠AOD+∠DOC+∠DOC+∠BOC=180°,
∴∠AOB+∠DOC=180°,
∴∠DOC变小,则∠AOB变大,故D正确,不符合题意.
故选:B.
9.解:A、∠1与∠2不互余,故本选项错误;
B、∠1与∠2不互余,故本选项错误;
C、∠1与∠2不互余,故本选项错误;
D、∠1与∠2互余,故本选项正确.
故选:D.
10.解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠1=∠AOC,
∠2=∠BOD,
∠AOE=∠COD,
∠BOE=∠COD,
∴图中相等的角有5对.
故选:A.
二.填空题
11.解:因为两个角的度数之比为3:2,
所以设这两个角的度数分别为(3x)°和(2x)°.
根据题意,列方程,得3x+2x=180,
解这个方程,得x=36,
所以3x=108.
即较大角度数为108°.
故答案为108°.
12.解:设这个角为x°,则其余角为(90﹣x)°,补角为(180﹣x)°,依题意有
180﹣x﹣3(90﹣x)=40,
解得x=65.
故这个角是65°.
故答案为:65°.
13.解:图形中相等的角有∠A=∠BCD,∠B=∠ACD,∠ACB=∠BDC,∠ACB=∠CDA,∠BDC=∠CDA,一共5对,互余的角有∠A和∠B,∠A和∠ACD,∠B和∠BCD,∠ACD和∠BCD,一共4对.
故答案为:5;4.
14.解:设这个角为x°,由题意得:
90﹣x+180﹣x=200,
解得:x=35,
故答案为:35.
15.解:∵∠COB+∠DOA=∠COB+∠COA+∠COB+∠DOB=∠AOB+∠COD=180°,
又∵∠COB与∠DOA的比是5:13,
∴∠DOA=180°×=130°,
∵OE平分∠DOA,
∴∠DOE=65°,
∴∠EOC=25°.
故答案为:25.
三.解答题
16.解:作OD⊥OA,则∠COD和∠AOC互余,如图所示.
∵∠AOB=128°,OC平分∠AOB,
∴∠AOC=∠AOB=64°,
∵∠COD和∠AOC互余,
∴∠COD=90°﹣∠AOC=26°.
17.解:∵OC平分∠AOB,∠BOC=26°,
∴∠AOB=2∠BOC=52°.
∴∠BOD=180°﹣52°=128°.
∵OE平分∠DOB,
∴∠BOE=∠DOB=×128°=64°.
18.解:(1)∵将一直角三角板的直角顶点放在点O处,一边ON在射线OB上,另一边OM在直线AB的上方,
∴∠MON=90°,
∴∠COM=∠MON﹣∠BOC=90°﹣60°=30°,
故答案为:30
(2)设∠NOC=x,那么∠MOA=6x,∠BON=60°﹣x.
由题意,可知6x+90°+60°﹣x=180°,
即5x=180°﹣90°﹣60°,
即5x=30°,
所以x=6°.
所以∠BON=60°﹣x=60°﹣6°=54°.
(3)∵直线ON平分∠BOC,∠BOC=60°,
∴∠BON=30°或∠BON=210°,
∵三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,
∴直线ON平分∠BOC时,旋转的时间是3或21秒,
故答案为:3或21
