人教版数学九年级上册 第23章 23.3课时学习 图案设计同步测试试题(一)(word解析版)
文档属性
| 名称 | 人教版数学九年级上册 第23章 23.3课时学习 图案设计同步测试试题(一)(word解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 344.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览

文档简介
课时学习
图案设计同步测试试题(一)
一.选择题
1.如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( )
A.1个
B.2个
C.3个
D.4个
2.下列是国内几所知名大学的图标,若不考虑图标上的文字、字母和数字,其中既可以通过翻折变换,又可以通过旋转变换得到的图形是( )
A.清华大学
B.浙江大学
C.北京大学
D.中南大学
3.一个图形无论经过平移变换,还是经过旋转变换,下列说法:a.对应线段平行,b.对应线段相等,c.图形的形状和大小都没有发生变化,d.对应角相等,其中正确的是( )
A.a.b.c.
B.b.c.d.
C.a.b.d.
D.a.c.d.
4.如图,点A,B在方格纸的格点位置上,若要再找一个格点C,使它们所构成的三角形为轴对称图形,则这样的格点C在图中共有( )
A.4个
B.6个
C.8个
D.10个
5.如图,在正方形方格中,阴影部分是涂黑
7
个小正方形所形成的图案,再将方格内空白的一个小正方形涂
黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.4
种
B.3
种
C.2
种
D.1
种
6.“飞流直下三千尺”、“坐地日行八万里(只考虑地球自转)”如果只从数学角度看,它们分别蕴含的图形变换是( )
A.平移、对称
B.对称、旋转
C.平移、旋转
D.旋转、对称
7.将如图所示“你最棒”的微信图案通过平移后可以得到的图案是( )
A.
B.
C.
D.
8.如图的四个图形中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )个.
A.1
B.2
C.3
D.4
9.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A.
B.
C.
D.
10.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有20×20的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )
A.13
B.14
C.15
D.16
二.填空题
11.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有
种.
12.图中能通过基本图形旋转得到的有
(请填写序号)
13.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要在其余13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案成轴对称图形,这样的白色小方格有
个,请在图中设计出一种方案.
14.如图,这个图形是由“基本图案”ABCDE绕着点
顺时针依次旋转
次得到的,则每次旋转的角度为
.
15.如图,在网格图中,平移图A,使它与图B拼合成一个长方形,应将图A向
(填“左”或“右”)平移
格;再向
(填“上”或“下”)平移
格.
三.解答题
16.如图,△ABC的三个顶点在网格上
(1)画出三角形关于原点O的中心对称图形△A1B1C1;
(2)直接写出点A1的坐标为
.
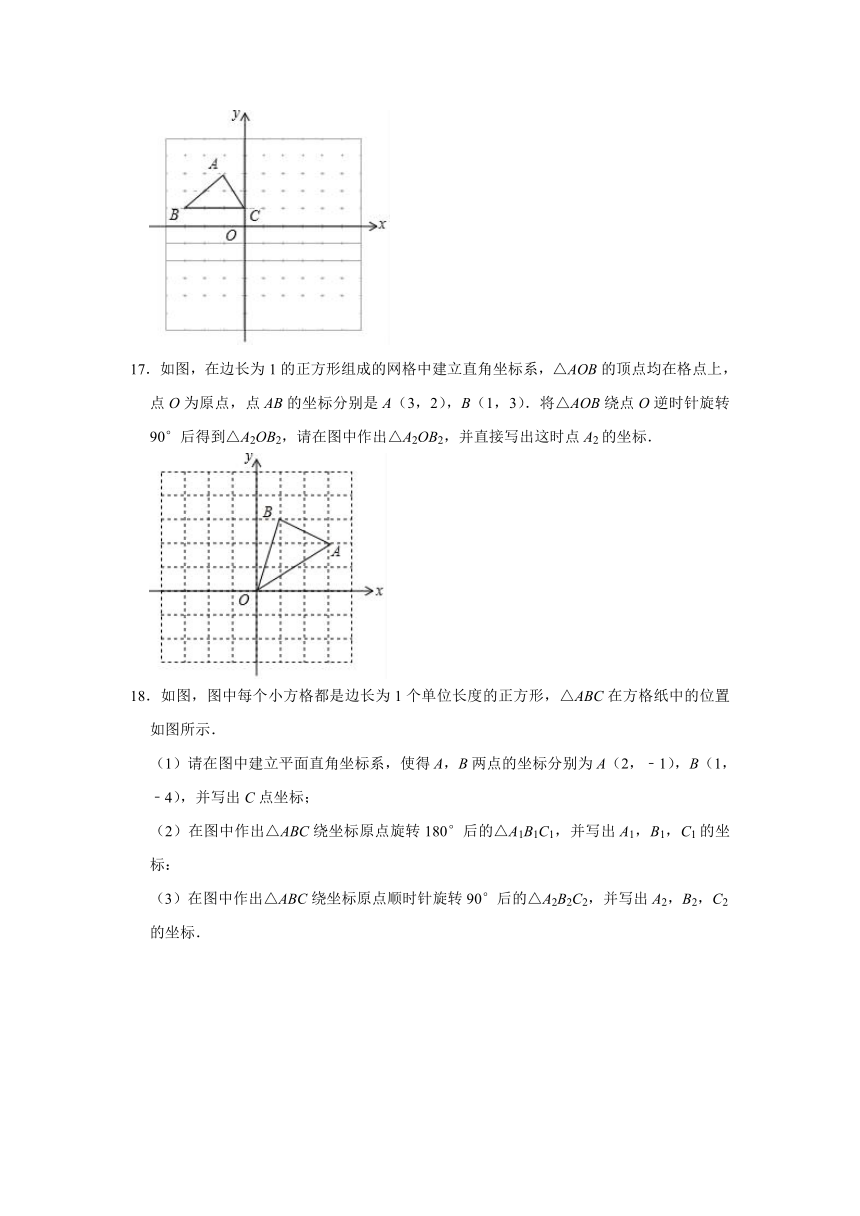
17.如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点AB的坐标分别是A(3,2),B(1,3).将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并直接写出这时点A2的坐标.
18.如图,图中每个小方格都是边长为1个单位长度的正方形,△ABC在方格纸中的位置如图所示.
(1)请在图中建立平面直角坐标系,使得A,B两点的坐标分别为A(2,﹣1),B(1,﹣4),并写出C点坐标;
(2)在图中作出△ABC绕坐标原点旋转180°后的△A1B1C1,并写出A1,B1,C1的坐标:
(3)在图中作出△ABC绕坐标原点顺时针旋转90°后的△A2B2C2,并写出A2,B2,C2的坐标.
19.阅读下列材料,完成相应学习任务
旋转对称
把正n边形绕着它的中心旋转°的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有°的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.
任务:
(1)如图2,正六边形关于其中心O有
的旋转对称,中心对称图形关于其对称中心有
的旋转对称;
(2)图3是利用旋转变换设计的具有旋转对称性的一个图形,将该图形绕其中心至少旋转
与原图形重合;
(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案是中心对称图形.
参考答案与试题解析
一.选择题
1.【解答】解:如图所示:
,
共3个,
故选:C.
2.【解答】解:A、是既可以通过翻折变换,又可以通过旋转变换得到的图形,正确;
B、可以通过翻折变换,但不可以通过旋转变换得到的图形,错误;
C、可以通过翻折变换,但不可以通过旋转变换得到的图形,错误;
D、不可以通过翻折变换,但可以通过旋转变换得到的图形,错误;
故选:A.
3.【解答】解:a、经过旋转变换对应线段不一定平行,
b、无论经过平移变换,还是经过旋转变换,对应线段相等,
c、无论经过平移变换,还是经过旋转变换,图形的形状和大小都没有发生变化,
d、无论经过平移变换,还是经过旋转变换,对应角相等,
综上所述,说法正确的是b、c、d.
故选:B.
4.【解答】解:如图所示,这样的格点C在图中共有10个,
故选:D.
5.【解答】解:在1,2,3处分别涂黑都可得一个轴对称图形.
故选:B.
6.【解答】解:根据平移和旋转定义可知:
“飞流直下三千尺”是平移;
“坐地日行八万里”是旋转.
故选:C.
7.【解答】解:将如图所示“你最棒”的微信图案通过平移后可以得到的图案是,
故选:C.
8.【解答】解:图形①可以分别旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形②可以旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形③可以旋转180°得到,不可以经过轴对称得到,故此选项错误;
图形④可以旋转180°得到,也可以经过轴对称,沿一条直线对折,能够完全重合.
故既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有3个.
故选:C.
9.【解答】解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
故选:B.
10.【解答】解:如图1,连接AC,CF,则AF=3,
∴两次变换相当于向右移动3格,向上移动3格,
又∵MN=20,
∴20÷3=,(不是整数)
∴按A﹣C﹣F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,
此时M位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处,
∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是10+4=14次,
故选:B.
二.填空题(共5小题)
11.【解答】解:如图,有三种方案,
故答案为3.
12.【解答】解:四幅图中,能通过基本图形旋转得到的有:(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
13.【解答】解:如图所示,有4个位置使之成为轴对称图形.
故答案为:4.
14.【解答】解:根据旋转的性质,可知:在点D处有6个角,故360°÷6=60°,所以它的旋转角为60°.
即这个图形是由“基本图案”ABCDE绕着点D顺时针依次旋转5次得到的,则每次旋转的角度为60°.
故答案为:D、5、60°.
15.【解答】解:∵A图形在B图形的左边可知应先向右平移图形A,点C距点D4个格,
∴应先向右平移4个格,此时点C与点D重合,
∵点D距点E2个格,
∴向上平移2格.
故答案为:右,4,上,2.
三.解答题(共4小题)
16.【解答】解:(1)如图,△A1B1C1为所作;
(2)点A1的坐标为(1,﹣3).
故答案为(1,﹣3).
17.【解答】解:如图所示:A2(﹣2,3);
.
18.【解答】解:(1)坐标系如图所示,C(3,﹣3);
(2)△A1B1C1如图所示,A1(﹣2,1),B1(﹣1,4),C1(﹣3,3);
(3)△A2B2C2如图所示,A(﹣1,﹣2),B(﹣4,﹣1),C2(﹣3,﹣3).
19.【解答】解:(1)正六边形关于其中心O有60°的旋转对称,中心对称图形关于其对称中心有180°的旋转对称;
故答案为:60°;180°;
(2)∵360°÷5=72°
图案设计同步测试试题(一)
一.选择题
1.如图是4×4的正方形网格,其中已有3个小方格涂成了黑色.现在要从其余13个白色小方格中选出一个也涂成黑色,与原来3个黑色方格组成的图形成为轴对称图形,则符合要求的白色小正方格有( )
A.1个
B.2个
C.3个
D.4个
2.下列是国内几所知名大学的图标,若不考虑图标上的文字、字母和数字,其中既可以通过翻折变换,又可以通过旋转变换得到的图形是( )
A.清华大学
B.浙江大学
C.北京大学
D.中南大学
3.一个图形无论经过平移变换,还是经过旋转变换,下列说法:a.对应线段平行,b.对应线段相等,c.图形的形状和大小都没有发生变化,d.对应角相等,其中正确的是( )
A.a.b.c.
B.b.c.d.
C.a.b.d.
D.a.c.d.
4.如图,点A,B在方格纸的格点位置上,若要再找一个格点C,使它们所构成的三角形为轴对称图形,则这样的格点C在图中共有( )
A.4个
B.6个
C.8个
D.10个
5.如图,在正方形方格中,阴影部分是涂黑
7
个小正方形所形成的图案,再将方格内空白的一个小正方形涂
黑,使得到的新图案成为一个轴对称图形的涂法有( )
A.4
种
B.3
种
C.2
种
D.1
种
6.“飞流直下三千尺”、“坐地日行八万里(只考虑地球自转)”如果只从数学角度看,它们分别蕴含的图形变换是( )
A.平移、对称
B.对称、旋转
C.平移、旋转
D.旋转、对称
7.将如图所示“你最棒”的微信图案通过平移后可以得到的图案是( )
A.
B.
C.
D.
8.如图的四个图形中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )个.
A.1
B.2
C.3
D.4
9.一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是( )
A.
B.
C.
D.
10.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处.现有20×20的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )
A.13
B.14
C.15
D.16
二.填空题
11.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有
种.
12.图中能通过基本图形旋转得到的有
(请填写序号)
13.如图是4×4正方形网格,其中已有3个小方格涂成了黑色.现在要在其余13个白色小方格中选出一个也涂成黑色,使整个黑色的小方格图案成轴对称图形,这样的白色小方格有
个,请在图中设计出一种方案.
14.如图,这个图形是由“基本图案”ABCDE绕着点
顺时针依次旋转
次得到的,则每次旋转的角度为
.
15.如图,在网格图中,平移图A,使它与图B拼合成一个长方形,应将图A向
(填“左”或“右”)平移
格;再向
(填“上”或“下”)平移
格.
三.解答题
16.如图,△ABC的三个顶点在网格上
(1)画出三角形关于原点O的中心对称图形△A1B1C1;
(2)直接写出点A1的坐标为
.
17.如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点AB的坐标分别是A(3,2),B(1,3).将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并直接写出这时点A2的坐标.
18.如图,图中每个小方格都是边长为1个单位长度的正方形,△ABC在方格纸中的位置如图所示.
(1)请在图中建立平面直角坐标系,使得A,B两点的坐标分别为A(2,﹣1),B(1,﹣4),并写出C点坐标;
(2)在图中作出△ABC绕坐标原点旋转180°后的△A1B1C1,并写出A1,B1,C1的坐标:
(3)在图中作出△ABC绕坐标原点顺时针旋转90°后的△A2B2C2,并写出A2,B2,C2的坐标.
19.阅读下列材料,完成相应学习任务
旋转对称
把正n边形绕着它的中心旋转°的整数倍后所得的正n边形重合.我们说,正n边形关于其中心有°的旋转对称.一般地,如果一个图形绕着某点O旋转角α(0<α<360°)后所得到的图形与原图形重合,则称此图形关于点O有角α的旋转对称.图1就是具有旋转对称性质的一些图形.
任务:
(1)如图2,正六边形关于其中心O有
的旋转对称,中心对称图形关于其对称中心有
的旋转对称;
(2)图3是利用旋转变换设计的具有旋转对称性的一个图形,将该图形绕其中心至少旋转
与原图形重合;
(3)请以图4为基本图案,在图5中利用平移、轴对称或旋转进行图案设计,使得设计出的图案是中心对称图形.
参考答案与试题解析
一.选择题
1.【解答】解:如图所示:
,
共3个,
故选:C.
2.【解答】解:A、是既可以通过翻折变换,又可以通过旋转变换得到的图形,正确;
B、可以通过翻折变换,但不可以通过旋转变换得到的图形,错误;
C、可以通过翻折变换,但不可以通过旋转变换得到的图形,错误;
D、不可以通过翻折变换,但可以通过旋转变换得到的图形,错误;
故选:A.
3.【解答】解:a、经过旋转变换对应线段不一定平行,
b、无论经过平移变换,还是经过旋转变换,对应线段相等,
c、无论经过平移变换,还是经过旋转变换,图形的形状和大小都没有发生变化,
d、无论经过平移变换,还是经过旋转变换,对应角相等,
综上所述,说法正确的是b、c、d.
故选:B.
4.【解答】解:如图所示,这样的格点C在图中共有10个,
故选:D.
5.【解答】解:在1,2,3处分别涂黑都可得一个轴对称图形.
故选:B.
6.【解答】解:根据平移和旋转定义可知:
“飞流直下三千尺”是平移;
“坐地日行八万里”是旋转.
故选:C.
7.【解答】解:将如图所示“你最棒”的微信图案通过平移后可以得到的图案是,
故选:C.
8.【解答】解:图形①可以分别旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形②可以旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形③可以旋转180°得到,不可以经过轴对称得到,故此选项错误;
图形④可以旋转180°得到,也可以经过轴对称,沿一条直线对折,能够完全重合.
故既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有3个.
故选:C.
9.【解答】解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,
故选:B.
10.【解答】解:如图1,连接AC,CF,则AF=3,
∴两次变换相当于向右移动3格,向上移动3格,
又∵MN=20,
∴20÷3=,(不是整数)
∴按A﹣C﹣F的方向连续变换10次后,相当于向右移动了10÷2×3=15格,向上移动了10÷2×3=15格,
此时M位于如图所示的5×5的正方形网格的点G处,再按如图所示的方式变换4次即可到达点N处,
∴从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是10+4=14次,
故选:B.
二.填空题(共5小题)
11.【解答】解:如图,有三种方案,
故答案为3.
12.【解答】解:四幅图中,能通过基本图形旋转得到的有:(1)(2)(3)(4).
故答案为:(1)(2)(3)(4).
13.【解答】解:如图所示,有4个位置使之成为轴对称图形.
故答案为:4.
14.【解答】解:根据旋转的性质,可知:在点D处有6个角,故360°÷6=60°,所以它的旋转角为60°.
即这个图形是由“基本图案”ABCDE绕着点D顺时针依次旋转5次得到的,则每次旋转的角度为60°.
故答案为:D、5、60°.
15.【解答】解:∵A图形在B图形的左边可知应先向右平移图形A,点C距点D4个格,
∴应先向右平移4个格,此时点C与点D重合,
∵点D距点E2个格,
∴向上平移2格.
故答案为:右,4,上,2.
三.解答题(共4小题)
16.【解答】解:(1)如图,△A1B1C1为所作;
(2)点A1的坐标为(1,﹣3).
故答案为(1,﹣3).
17.【解答】解:如图所示:A2(﹣2,3);
.
18.【解答】解:(1)坐标系如图所示,C(3,﹣3);
(2)△A1B1C1如图所示,A1(﹣2,1),B1(﹣1,4),C1(﹣3,3);
(3)△A2B2C2如图所示,A(﹣1,﹣2),B(﹣4,﹣1),C2(﹣3,﹣3).
19.【解答】解:(1)正六边形关于其中心O有60°的旋转对称,中心对称图形关于其对称中心有180°的旋转对称;
故答案为:60°;180°;
(2)∵360°÷5=72°
同课章节目录
