湘教版(2012)初中数学九年级上册 3.5 相似三角形的应用(3) 教案
文档属性
| 名称 | 湘教版(2012)初中数学九年级上册 3.5 相似三角形的应用(3) 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 530.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览

文档简介
课题:3.5 相似三角形应用(3)
1、知识与技能:进一步掌握相似三角形的判定及性质,能将实际问题转化为三角形相似求解;
2、过程与方法:经过对不能直接到达的高度的测量,将实际问题转化为三角形相似的问题,进一步培养学生的数学建模思想,培养学生的探究意识和分析解决问题的能力;、
3、情感态度与价值观:经历用三角形相似的知识求达不到高度的测量与求法,培养学生的数学应用意识,感悟知识就是力量的深刻内涵,享受学习带来的快乐与成就。
1.重点:将实际问题转化为三角形相似的问题
2.难点:寻找需要解决问题的两个相似的三角形
探究讨论法
【一、创设情境,导入新课】
生活中,有很多很高的建筑物,如法国巴黎的埃菲尔铁塔,大都市高耸如云摩登大楼,还有我们校园内的参天古树以及魏然屹立的高高的旗杆,我们不可直接对其高度进行测量,我们能否利用学过的相似三角形及解决这个问题呢?(图片见课件)
【二、实地操作,合作探究】
以测量旗杆高度,引导学生带着皮卷尺和标杆,探讨测量的方法,发掘其他可行的办法。回到课堂,讨论、总结、归纳。
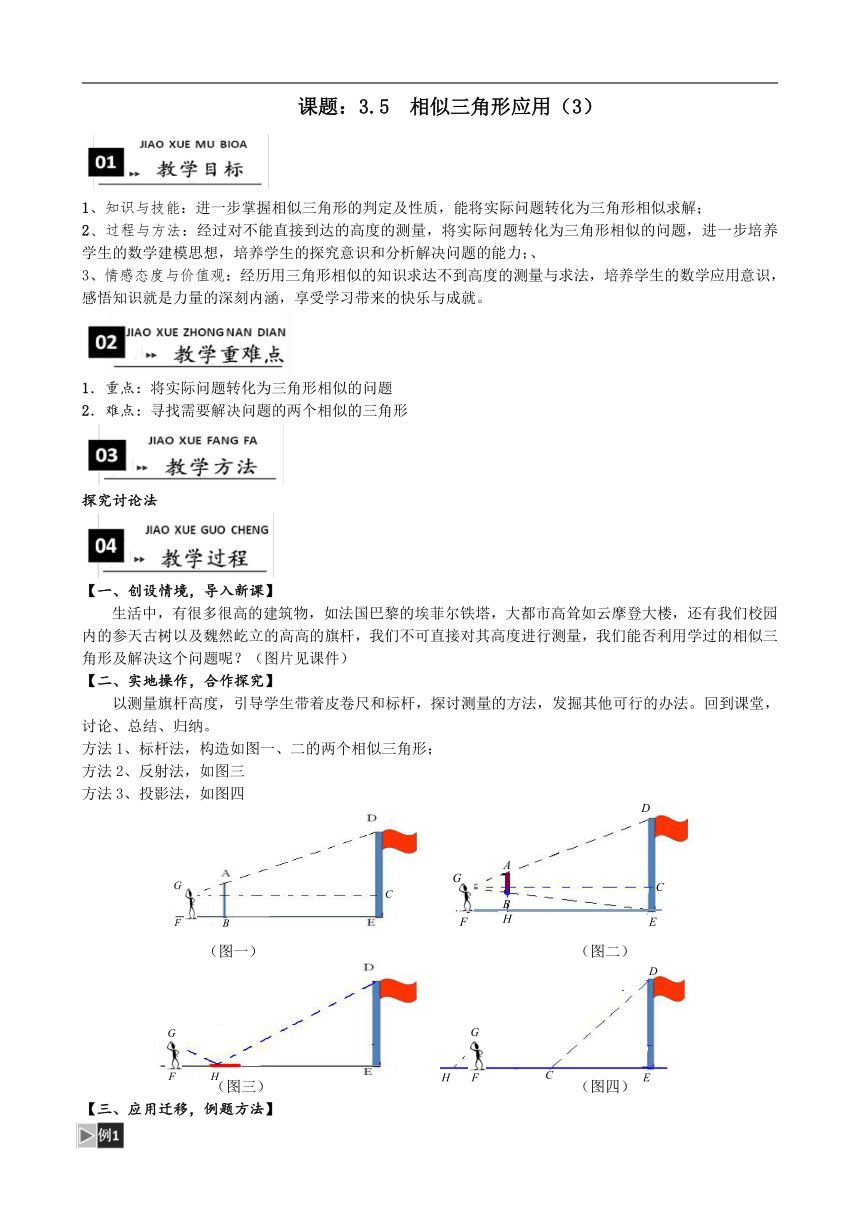
方法1、标杆法,构造如图一、二的两个相似三角形;
方法2、反射法,如图三
方法3、投影法,如图四
(图一)
(图二)
(图三)
(图四)
【三、应用迁移,例题方法】
阳光明媚的一天,数学兴趣小组的同学去测量一棵树的高度(这棵树底部可以到达,顶部不可以到达),他们带了以下工具:皮尺,标杆,一副三角尺,小平面镜。请你在他们提供的工具中选出所需的工具,设计、一种测量方案。
(1)所需工具是(
)
(2)请在下图中画出测量示意图;
(3)设树高AB为x,请用所测数据
(小写字母表示)求出x。
解析:(1)皮尺,标杆;
(2)测量示意图如右所示;
(3)测得标杆长为a,标杆和树的影长分别为EF=c,AC=b,由
得DE:AB=EF:AC,
所以a:x=
c:
b,所以x=
如图,小明设计用手电来某古城高度示意图,点P处放一水平平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB
BD,
CD
BD,且测得AB=1.2m,
BP=1.8m,PD=12m,那么该古城墙的高度是(
)
A、6米
B、8米
C、18米
D、24米
【四、当堂检测,反馈评价】
1、要测量旗杆的高度,在阳光下,一名同学测得一根1米长的标杆的影长是0.4米,同时另一名同学测旗杆高度时,发现影子不全落在地面上,有一部分落在教学楼上,测得影子长为2米,落在地面的影子长为4.4米,则旗杆的高度为(
D
)米。
A、10
B、11
C、12
D、13
(第1题图)
(第3题图)
2.小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶(??A?)
A.0.5m????????????????B.0.55m?????????????C.0.6m?????????????????D.2.2m
3.如图所示,身高为1.6m的某学生测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为(?C??)
A.4.8m????????????????B.6.4m???????????????C.8m????????????????????D.10m
4、如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光下,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在E点处,影子落在坡面上,小华站在平地上,影子落在地面上,两人的影长分别为2米和1米,那么塔高AB为(
A
)米
A、24
B、22
C、20
D、18
(第4题图)
(第5题图)
5、为了测量校园内一棵不可攀登的树的高度,学校数学兴趣小组做了如下的探索:如图所示,把镜子放在离树(AB)8.7米的点E处,然后沿着BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,则树的高度约为(精确到0.1米)(
C
)
A.4.8m????????????????B.5.1m??????????????
?C.5.2m?????????????????
D.5.5
m
【五、课后作业,巩固提升】见《学法大视野》P60本课练习
【六、课堂小结,自我反思】
课堂小结:1)知识与方法归纳
2)困惑与疑虑解难
2、反思小结:
1、知识与技能:进一步掌握相似三角形的判定及性质,能将实际问题转化为三角形相似求解;
2、过程与方法:经过对不能直接到达的高度的测量,将实际问题转化为三角形相似的问题,进一步培养学生的数学建模思想,培养学生的探究意识和分析解决问题的能力;、
3、情感态度与价值观:经历用三角形相似的知识求达不到高度的测量与求法,培养学生的数学应用意识,感悟知识就是力量的深刻内涵,享受学习带来的快乐与成就。
1.重点:将实际问题转化为三角形相似的问题
2.难点:寻找需要解决问题的两个相似的三角形
探究讨论法
【一、创设情境,导入新课】
生活中,有很多很高的建筑物,如法国巴黎的埃菲尔铁塔,大都市高耸如云摩登大楼,还有我们校园内的参天古树以及魏然屹立的高高的旗杆,我们不可直接对其高度进行测量,我们能否利用学过的相似三角形及解决这个问题呢?(图片见课件)
【二、实地操作,合作探究】
以测量旗杆高度,引导学生带着皮卷尺和标杆,探讨测量的方法,发掘其他可行的办法。回到课堂,讨论、总结、归纳。
方法1、标杆法,构造如图一、二的两个相似三角形;
方法2、反射法,如图三
方法3、投影法,如图四
(图一)
(图二)
(图三)
(图四)
【三、应用迁移,例题方法】
阳光明媚的一天,数学兴趣小组的同学去测量一棵树的高度(这棵树底部可以到达,顶部不可以到达),他们带了以下工具:皮尺,标杆,一副三角尺,小平面镜。请你在他们提供的工具中选出所需的工具,设计、一种测量方案。
(1)所需工具是(
)
(2)请在下图中画出测量示意图;
(3)设树高AB为x,请用所测数据
(小写字母表示)求出x。
解析:(1)皮尺,标杆;
(2)测量示意图如右所示;
(3)测得标杆长为a,标杆和树的影长分别为EF=c,AC=b,由
得DE:AB=EF:AC,
所以a:x=
c:
b,所以x=
如图,小明设计用手电来某古城高度示意图,点P处放一水平平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB
BD,
CD
BD,且测得AB=1.2m,
BP=1.8m,PD=12m,那么该古城墙的高度是(
)
A、6米
B、8米
C、18米
D、24米
【四、当堂检测,反馈评价】
1、要测量旗杆的高度,在阳光下,一名同学测得一根1米长的标杆的影长是0.4米,同时另一名同学测旗杆高度时,发现影子不全落在地面上,有一部分落在教学楼上,测得影子长为2米,落在地面的影子长为4.4米,则旗杆的高度为(
D
)米。
A、10
B、11
C、12
D、13
(第1题图)
(第3题图)
2.小刚身高1.7m,测得他站立在阳光下的影子长为0.85m,紧接着他把手臂竖直举起,测得影子长为1.1m,那么小刚举起的手臂超出头顶(??A?)
A.0.5m????????????????B.0.55m?????????????C.0.6m?????????????????D.2.2m
3.如图所示,身高为1.6m的某学生测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,则树的高度为(?C??)
A.4.8m????????????????B.6.4m???????????????C.8m????????????????????D.10m
4、如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光下,塔影长DE=18米,小明和小华的身高都是1.6米,同一时刻,小明站在E点处,影子落在坡面上,小华站在平地上,影子落在地面上,两人的影长分别为2米和1米,那么塔高AB为(
A
)米
A、24
B、22
C、20
D、18
(第4题图)
(第5题图)
5、为了测量校园内一棵不可攀登的树的高度,学校数学兴趣小组做了如下的探索:如图所示,把镜子放在离树(AB)8.7米的点E处,然后沿着BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,则树的高度约为(精确到0.1米)(
C
)
A.4.8m????????????????B.5.1m??????????????
?C.5.2m?????????????????
D.5.5
m
【五、课后作业,巩固提升】见《学法大视野》P60本课练习
【六、课堂小结,自我反思】
课堂小结:1)知识与方法归纳
2)困惑与疑虑解难
2、反思小结:
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
