北师大版六年级下册数学正比例与反比例授课课件(39张)
文档属性
| 名称 | 北师大版六年级下册数学正比例与反比例授课课件(39张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览


文档简介
正比例与反比例
<
=
>
+
×
-
÷
1
2
3
北师版小学数学六年级下
激趣导入
比和比例
比例尺
比和分数、除法有什么联系。
知识讲解
比
比例
两个数相除叫做两个数的比。
表示两个比相等的式子。
知识讲解
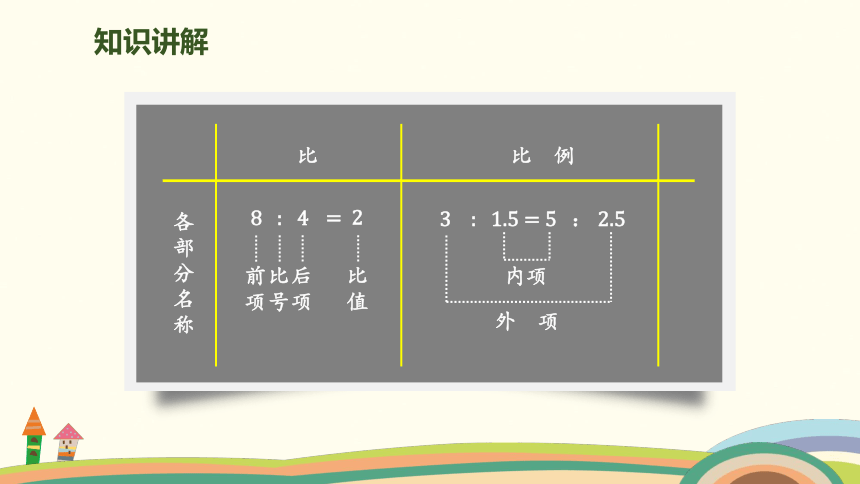
8 : 4
比
3 : 1.5 = 5 : 2.5
比 例
各部分名称
前项
后项
比号
= 2
比值
内项
外 项
知识讲解
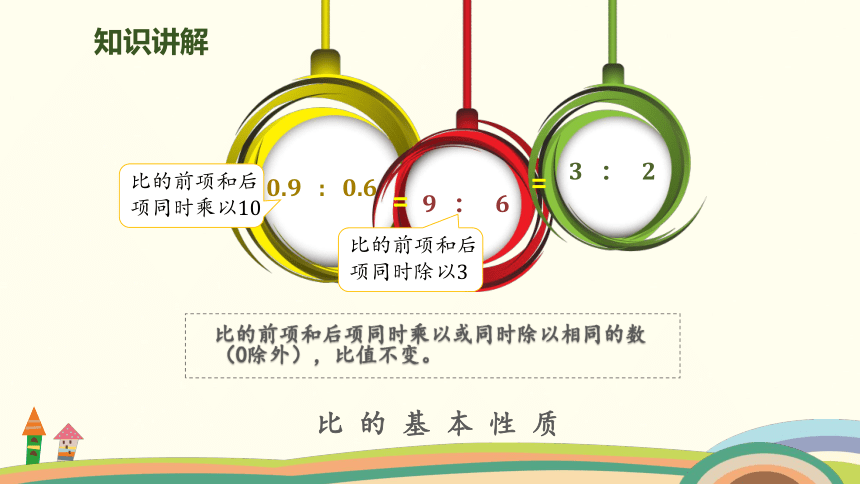
0.9 : 0.6
9 : 6
3 : 2
比 的 基 本 性 质
=
=
比的前项和后项同时乘以10
比的前项和后项同时除以3
比的前项和后项同时乘以或同时除以相同的数(0除外),比值不变。
知识讲解
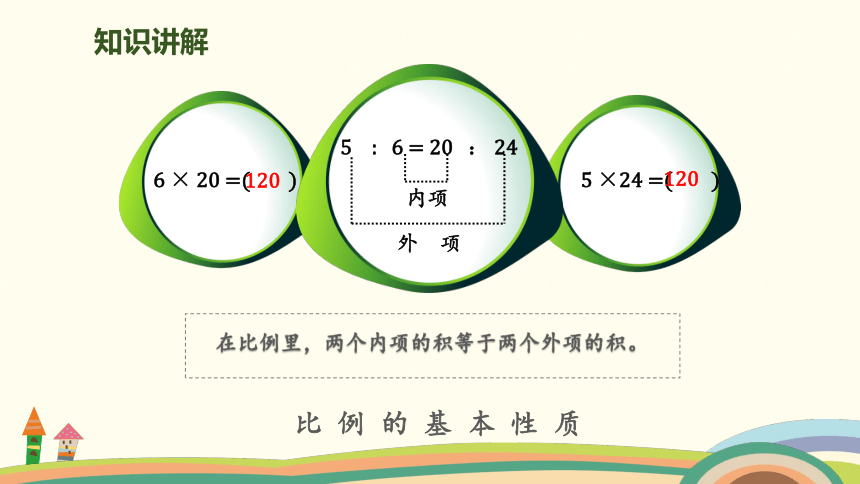
5 : 6 = 20 : 24
内项
外 项
6 × 20 =( )
5 ×24 =( )
120
120
比 例 的 基 本 性 质
在比例里,两个内项的积等于两个外项的积。
知识讲解
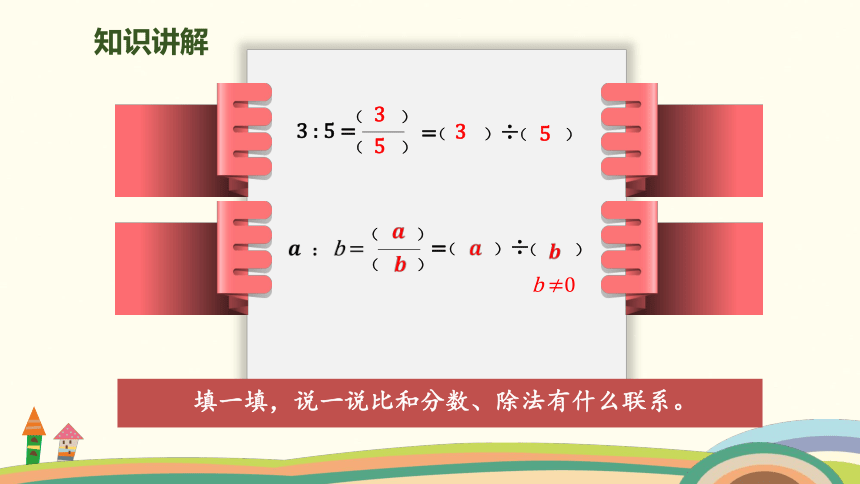
填一填,说一说比和分数、除法有什么联系。
3 : 5 =
( )
( )
= ÷
( )
( )
( )
( )
= ÷
( )
( )
b ≠0
3
5
3
5
知识讲解
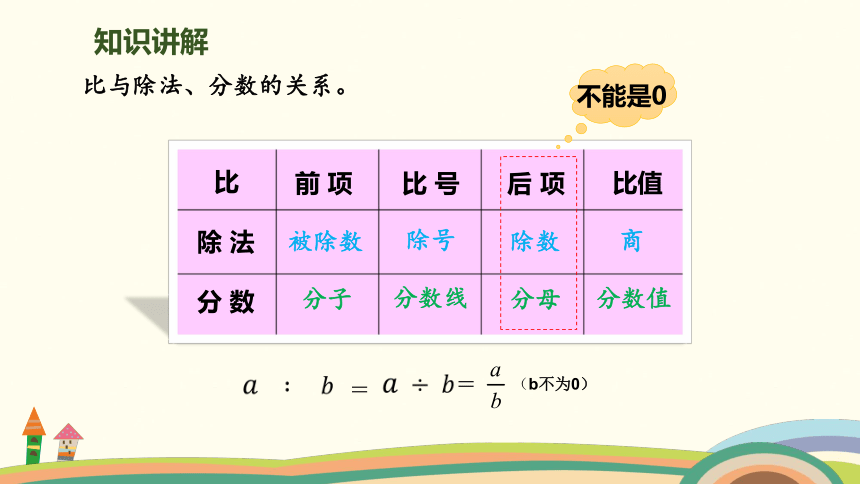
比与除法、分数的关系。
不能是0
比
除 法
分 数
前 项
比 号
后 项
比值
被除数
除号
除数
分子
分数线
分母
商
分数值
不能是0
=
=
(b不为0)
知识讲解
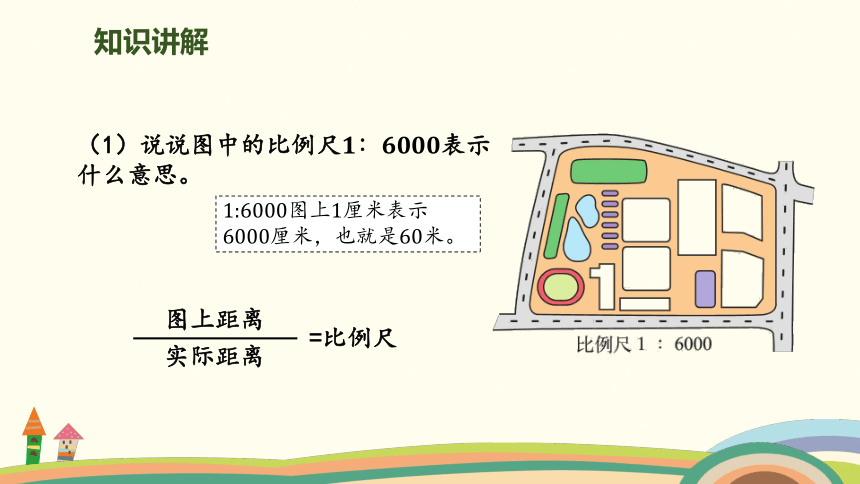
(1)说说图中的比例尺1∶6000表示什么意思。
1:6000图上1厘米表示6000厘米,也就是60米。
图上距离
实际距离
=比例尺
知识讲解
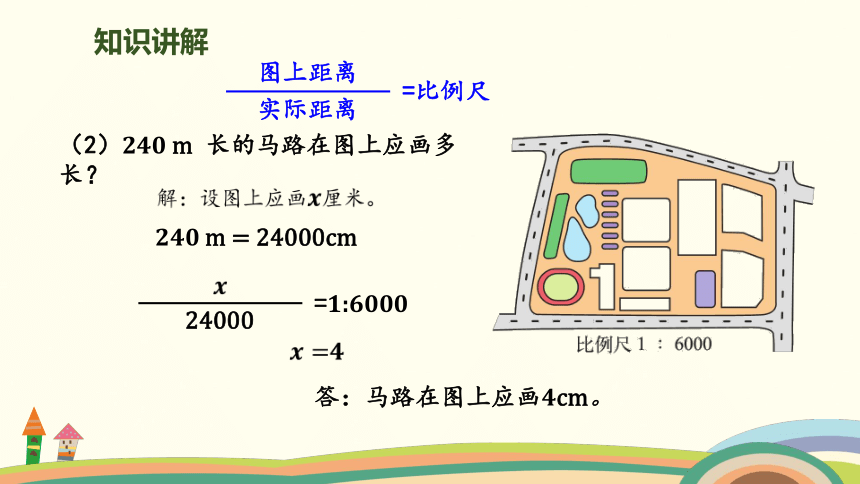
(2)240 m 长的马路在图上应画多长?
图上距离
实际距离
=比例尺
24000
=1:6000
240 m = 24000cm
答:马路在图上应画4cm。
知识讲解
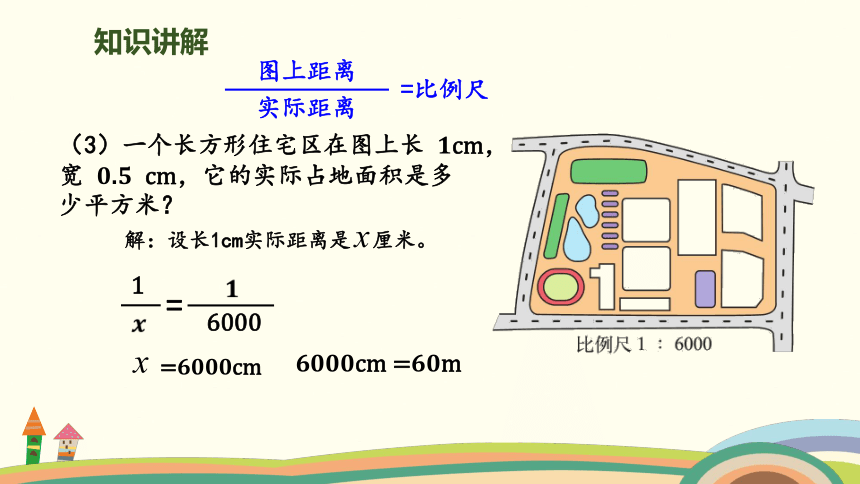
(3)一个长方形住宅区在图上长 1cm,
宽 0.5 cm,它的实际占地面积是多
少平方米?
图上距离
实际距离
=比例尺
1
6000
=
6000cm =60m
解:设长1cm实际距离是 厘米。
=6000cm
知识讲解
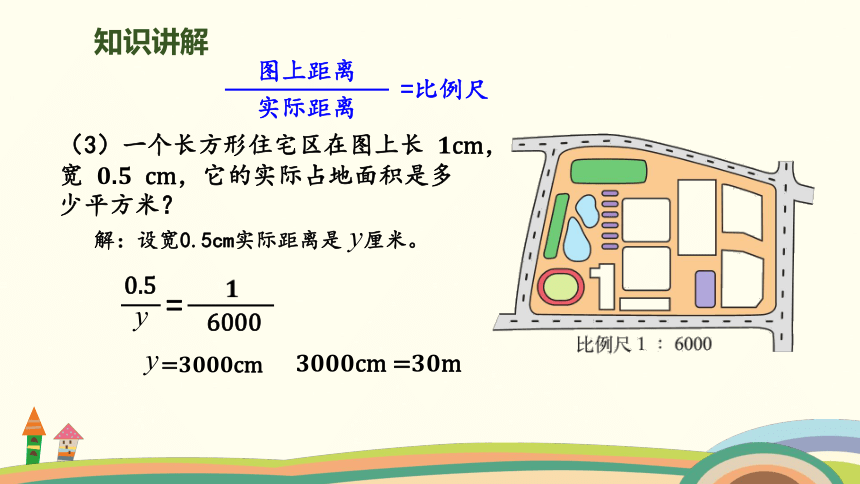
(3)一个长方形住宅区在图上长 1cm,
宽 0.5 cm,它的实际占地面积是多
少平方米?
图上距离
实际距离
=比例尺
3000cm =30m
解:设宽0.5cm实际距离是 厘米。
0.5
6000
=
=3000cm
知识讲解
(3)一个长方形住宅区在图上长 1cm,
宽 0.5 cm,它的实际占地面积是多
少平方米?
图上距离
实际距离
=比例尺
60 × 30 = 1800(平方米)
答:它的实际占地面积是1800平方米。
激趣导入
正、反比例的异同点
反比例的意义
正比例的意义
知识讲解
一辆汽车在高速路上行驶,速度保持在 100 千米 / 时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
时间(时)
1
路程(km)
100
2
3
4
…
5
速度一定
知识讲解
100 千米 / 时
速度一定
时间(时)
1
路程(km)
100
2
200
3
300
4
400
…
…
5
500
知识讲解
时间(时)
1
路程(km)
100
2
200
3
300
4
400
…
…
5
500
100 千米 / 时
如果用 t 表示汽车行驶的时间,s 表示汽车行驶的路程,那么_____________________。
知识讲解
= 速度(一定)
路程
时间
两种相关联的量
一种量变化
另一种量也随着变化
100
100
100
100
100
速度
当速度一定时,路程和时间成正比例的量。
时间(时)
1
路程(km)
100
2
200
3
300
4
400
…
…
5
500
知识讲解
一辆汽车在高速路上行驶,速度保持在 100 千米 / 时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
路程/km
时间/时
1
2
3
4
5
0
100
300
200
400
500
正比例的图像是一条直线。
知识讲解
正比例
意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值(商)一定,这两种量就叫做成正比例的量。(它们的关系叫做正比例关系)
公路长120千米
知识讲解
举例 说说生活中有哪些成反比例的量
时间(时)
1
速度(km/ 时)
120
2
60
3
40
4
30
…
…
1小时
2小时
3小时
4小时
知识讲解
= 路程(一定)
速度
时间
两种相关联的量
一种量变化
另一种量也随着变化
120
120
120
120
120
路程
当路程一定时,时间和速度成反比例的量。
时间(时)
1
速度(km/ 时)
120
2
60
3
40
4
30
…
…
×
速度km/ 时
时间/时
1
2
3
4
0
20
60
40
80
100
120
知识讲解
时间(时)
1
速度(km/ 时)
120
2
60
3
40
4
30
…
…
反比例的图像是一条曲线。
知识讲解
反比例
意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。(它们的关系叫做反比例关系)
知识讲解
正比例
反比例
相同点
1、一个不变量,两个变量。
1、一个不变量,两个变量。
2、一种量随着另一种量变化。
2、一种量随着另一种量变化。
知识讲解
正比例
反比例
不同点
比值(商)一定。
积一定
(一定)
(一定)
正比例的图像是一条直线。
反比例的图像是一条曲线。
练习巩固
1
2
3
两个正方形的边长比是 1∶3 ,
周长比是( ),面积比是( )。
9 元可以买 2 kg 鸡蛋,总价与数量
的比是( ),比值是( )。
汽车 3 时行 150 km,路程与时间的比是( ),比值是( )。
练习巩固
1
2
3
一捆 100 m 长的电线,用去的长度与剩下的长度。 ( )
三角形的面积一定,它的底和高。
( )。
一个数与它的倒数。 ( )。
判断下面每题中的两个量是否成正比例或反比例。
反比例
反比例
不成比例
练习巩固
化 简
30 : 90
0.45 : 0.9
30 : 90=30÷30 : 90÷30 =1 :3
0.45 : 0.9=0.45×100 : 0.9×100 =45 :90=45÷45 : 90÷45 =1 :2
120000
练习巩固
妙妙家到学校的距离是1200米,图上距离是多少厘米?
妙妙家
学校
电影院
奇思家
比例尺1∶8000
8000
=
1200米=120000厘米
答:图上距离是15厘米。
练习巩固
应付金额与所买邮票的数量成正比例吗?
邮票单价×邮票的数量=应付金额
(一定)
当邮票单价一定时,应付金额与邮票数量成正比例的量。
练习巩固
每袋化肥的质量一定,化肥的总质量和袋数成比例吗。
每袋化肥的质量×化肥的袋数=总质量
(一定)
当每袋化肥的质量一定时,化肥的总质量和袋数成正比例的量。
练习巩固
行驶的路程一定,车轮的周长与车轮需要转动的圈数成比例吗。
1
车轮的周长×转动的圈数=行驶的路程
(一定)
当行驶的路程一定时,车轮的周长与车轮需要转动的圈数成正比例的量。
知识总结
比 和 比 例
比
比例
两个数相除
叫做两个数的比。
表示两个比相
等的式子。
知识总结
比的基本性质
比例的基本性质
比的前项和后项同时乘以或同时除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
知识总结
比例尺
图上距离
实际距离
=比例尺
知识总结
正比例
反比例
相同点
1、一个不变量,两个变量。
2、一种量随着另一种量变化。
不同点
比值(商)一定。
积一定
(一定)
(一定)
正比例的图像是一条直线。
反比例的图像是一条曲线。
课后作业
第84页第2、3、4题
谢谢观看
<
=
>
+
×
-
÷
1
2
3
北师版小学数学六年级下
<
=
>
+
×
-
÷
1
2
3
北师版小学数学六年级下
激趣导入
比和比例
比例尺
比和分数、除法有什么联系。
知识讲解
比
比例
两个数相除叫做两个数的比。
表示两个比相等的式子。
知识讲解
8 : 4
比
3 : 1.5 = 5 : 2.5
比 例
各部分名称
前项
后项
比号
= 2
比值
内项
外 项
知识讲解
0.9 : 0.6
9 : 6
3 : 2
比 的 基 本 性 质
=
=
比的前项和后项同时乘以10
比的前项和后项同时除以3
比的前项和后项同时乘以或同时除以相同的数(0除外),比值不变。
知识讲解
5 : 6 = 20 : 24
内项
外 项
6 × 20 =( )
5 ×24 =( )
120
120
比 例 的 基 本 性 质
在比例里,两个内项的积等于两个外项的积。
知识讲解
填一填,说一说比和分数、除法有什么联系。
3 : 5 =
( )
( )
= ÷
( )
( )
( )
( )
= ÷
( )
( )
b ≠0
3
5
3
5
知识讲解
比与除法、分数的关系。
不能是0
比
除 法
分 数
前 项
比 号
后 项
比值
被除数
除号
除数
分子
分数线
分母
商
分数值
不能是0
=
=
(b不为0)
知识讲解
(1)说说图中的比例尺1∶6000表示什么意思。
1:6000图上1厘米表示6000厘米,也就是60米。
图上距离
实际距离
=比例尺
知识讲解
(2)240 m 长的马路在图上应画多长?
图上距离
实际距离
=比例尺
24000
=1:6000
240 m = 24000cm
答:马路在图上应画4cm。
知识讲解
(3)一个长方形住宅区在图上长 1cm,
宽 0.5 cm,它的实际占地面积是多
少平方米?
图上距离
实际距离
=比例尺
1
6000
=
6000cm =60m
解:设长1cm实际距离是 厘米。
=6000cm
知识讲解
(3)一个长方形住宅区在图上长 1cm,
宽 0.5 cm,它的实际占地面积是多
少平方米?
图上距离
实际距离
=比例尺
3000cm =30m
解:设宽0.5cm实际距离是 厘米。
0.5
6000
=
=3000cm
知识讲解
(3)一个长方形住宅区在图上长 1cm,
宽 0.5 cm,它的实际占地面积是多
少平方米?
图上距离
实际距离
=比例尺
60 × 30 = 1800(平方米)
答:它的实际占地面积是1800平方米。
激趣导入
正、反比例的异同点
反比例的意义
正比例的意义
知识讲解
一辆汽车在高速路上行驶,速度保持在 100 千米 / 时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
时间(时)
1
路程(km)
100
2
3
4
…
5
速度一定
知识讲解
100 千米 / 时
速度一定
时间(时)
1
路程(km)
100
2
200
3
300
4
400
…
…
5
500
知识讲解
时间(时)
1
路程(km)
100
2
200
3
300
4
400
…
…
5
500
100 千米 / 时
如果用 t 表示汽车行驶的时间,s 表示汽车行驶的路程,那么_____________________。
知识讲解
= 速度(一定)
路程
时间
两种相关联的量
一种量变化
另一种量也随着变化
100
100
100
100
100
速度
当速度一定时,路程和时间成正比例的量。
时间(时)
1
路程(km)
100
2
200
3
300
4
400
…
…
5
500
知识讲解
一辆汽车在高速路上行驶,速度保持在 100 千米 / 时。说一说汽车行驶的路程随时间变化的情况,并用多种方式表示这两个量之间的关系。
路程/km
时间/时
1
2
3
4
5
0
100
300
200
400
500
正比例的图像是一条直线。
知识讲解
正比例
意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比的比值(商)一定,这两种量就叫做成正比例的量。(它们的关系叫做正比例关系)
公路长120千米
知识讲解
举例 说说生活中有哪些成反比例的量
时间(时)
1
速度(km/ 时)
120
2
60
3
40
4
30
…
…
1小时
2小时
3小时
4小时
知识讲解
= 路程(一定)
速度
时间
两种相关联的量
一种量变化
另一种量也随着变化
120
120
120
120
120
路程
当路程一定时,时间和速度成反比例的量。
时间(时)
1
速度(km/ 时)
120
2
60
3
40
4
30
…
…
×
速度km/ 时
时间/时
1
2
3
4
0
20
60
40
80
100
120
知识讲解
时间(时)
1
速度(km/ 时)
120
2
60
3
40
4
30
…
…
反比例的图像是一条曲线。
知识讲解
反比例
意义
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量。(它们的关系叫做反比例关系)
知识讲解
正比例
反比例
相同点
1、一个不变量,两个变量。
1、一个不变量,两个变量。
2、一种量随着另一种量变化。
2、一种量随着另一种量变化。
知识讲解
正比例
反比例
不同点
比值(商)一定。
积一定
(一定)
(一定)
正比例的图像是一条直线。
反比例的图像是一条曲线。
练习巩固
1
2
3
两个正方形的边长比是 1∶3 ,
周长比是( ),面积比是( )。
9 元可以买 2 kg 鸡蛋,总价与数量
的比是( ),比值是( )。
汽车 3 时行 150 km,路程与时间的比是( ),比值是( )。
练习巩固
1
2
3
一捆 100 m 长的电线,用去的长度与剩下的长度。 ( )
三角形的面积一定,它的底和高。
( )。
一个数与它的倒数。 ( )。
判断下面每题中的两个量是否成正比例或反比例。
反比例
反比例
不成比例
练习巩固
化 简
30 : 90
0.45 : 0.9
30 : 90=30÷30 : 90÷30 =1 :3
0.45 : 0.9=0.45×100 : 0.9×100 =45 :90=45÷45 : 90÷45 =1 :2
120000
练习巩固
妙妙家到学校的距离是1200米,图上距离是多少厘米?
妙妙家
学校
电影院
奇思家
比例尺1∶8000
8000
=
1200米=120000厘米
答:图上距离是15厘米。
练习巩固
应付金额与所买邮票的数量成正比例吗?
邮票单价×邮票的数量=应付金额
(一定)
当邮票单价一定时,应付金额与邮票数量成正比例的量。
练习巩固
每袋化肥的质量一定,化肥的总质量和袋数成比例吗。
每袋化肥的质量×化肥的袋数=总质量
(一定)
当每袋化肥的质量一定时,化肥的总质量和袋数成正比例的量。
练习巩固
行驶的路程一定,车轮的周长与车轮需要转动的圈数成比例吗。
1
车轮的周长×转动的圈数=行驶的路程
(一定)
当行驶的路程一定时,车轮的周长与车轮需要转动的圈数成正比例的量。
知识总结
比 和 比 例
比
比例
两个数相除
叫做两个数的比。
表示两个比相
等的式子。
知识总结
比的基本性质
比例的基本性质
比的前项和后项同时乘以或同时除以相同的数(0除外),比值不变。
在比例里,两个内项的积等于两个外项的积。
知识总结
比例尺
图上距离
实际距离
=比例尺
知识总结
正比例
反比例
相同点
1、一个不变量,两个变量。
2、一种量随着另一种量变化。
不同点
比值(商)一定。
积一定
(一定)
(一定)
正比例的图像是一条直线。
反比例的图像是一条曲线。
课后作业
第84页第2、3、4题
谢谢观看
<
=
>
+
×
-
÷
1
2
3
北师版小学数学六年级下
