湘教版(2012)初中数学九年级上册 3.6 坐标平面中的位似变换 教案
文档属性
| 名称 | 湘教版(2012)初中数学九年级上册 3.6 坐标平面中的位似变换 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 303.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览

文档简介
《坐标平面中的位似变换》
湖南省教育出版社义务教育教科书《数学》九年级上册第98页到第99页的教学内容,过去湘教版教科书中没有,对于我们来说是新的授课内容,比较生疏,容易忽视,再说,我们的老师上课时不愿意画图,我们的学生更是如此,鉴于此,对本节课的教学设计有以下思考,供广大同行在教学中参考。
一、对本节课的课题设计的思考:
很明显,本节课是在坐标平面中研究位拟变换,因此,命名为“坐标平面中的位似变换”能使学生更加明确本节课的学习目标:
1、如何在坐标平面中进行位拟变换;
2、坐标平面中位似变换时,对应点的坐标与相似比有何关系。
二、对“动脑筋”教学设计的思考:
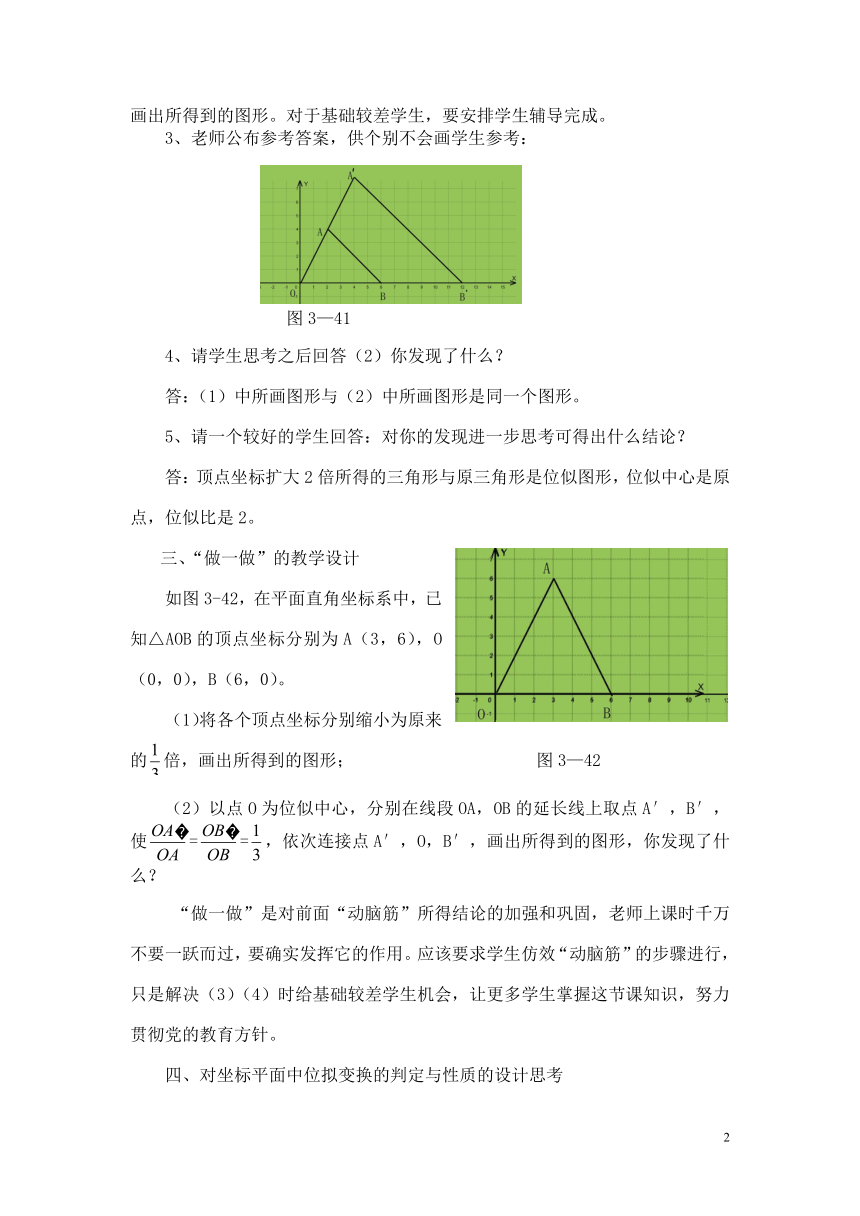
如图3-40,在平面直角坐标系中,已知△AOB的顶点坐标分别为A(2,4),O(0,0),B(6,0)。
(1)将各个顶点坐标分别扩大为原来的2倍,画出所得到的图形;
(2)以点O为位似中心,分别在线段OA,OB的延长线上取点A′,B′,使==2,依
图
3—40
次连接点A′,O,B′,画出所得到的图形,你发现了什么?
处理此段课文时,老师往往忽视学生动手的必要性,不给学生动手的机会,或学生动手不彻底,从而很难有所发现。不要忘记,实践才能出真知,数学教学中必须时刻遵循的这个原则。
这段课文我建议作如下设计:
1、要求每个学生在图3-40中认真完成(1)将各个顶点坐标分别扩大为原来的2倍,画出所得到的图形。对于基础较差学生,要安排学生辅导完成。
2、要求每个学生在图3-40中认真完成(2)以点O为位似中心,分别在线取OA、OB的延长线上取点A',B',使==2,依次连接A',O,B',画出所得到的图形。对于基础较差学生,要安排学生辅导完成。
3、老师公布参考答案,供个别不会画学生参考:
图3—41
4、请学生思考之后回答(2)你发现了什么?
答:(1)中所画图形与(2)中所画图形是同一个图形。
5、请一个较好的学生回答:对你的发现进一步思考可得出什么结论?
答:顶点坐标扩大2倍所得的三角形与原三角形是位似图形,位似中心是原点,位似比是2。
三、“做一做”的教学设计
如图3-42,在平面直角坐标系中,已知△AOB的顶点坐标分别为A(3,6),O(0,0),B(6,0)。
(1)将各个顶点坐标分别缩小为原来的倍,画出所得到的图形;
图3—42
(2)以点O为位似中心,分别在线段OA,OB的延长线上取点A′,B′,使==,依次连接点A′,O,B′,画出所得到的图形,你发现了什么?
“做一做”是对前面“动脑筋”所得结论的加强和巩固,老师上课时千万不要一跃而过,要确实发挥它的作用。应该要求学生仿效“动脑筋”的步骤进行,只是解决(3)(4)时给基础较差学生机会,让更多学生掌握这节课知识,努力贯彻党的教育方针。
四、对坐标平面中位拟变换的判定与性质的设计思考
1、前面的“动脑筋”、“做一做”的位似图形的位似中心都比较特殊:都是三角形的一个顶点,如果位似中心任取一点,是否有以上结论呢?因此,可设计一个如下“做一做”让全体学生去发现。
如图,在平面直角坐标系中,已知△ABC的顶点坐标分别为A(0,2),B(-1,-1),C(3,1)。
(1)将各个顶点坐标分别扩大成原来的2倍,画出所得图形。
(2)以点O为位似中心,分别在线OA、OB、OC的延长线上取点A'、B'、C',使
=
=
=2
顺次连接A'、B'、C',画出所得到的图形,你发现了什么?
让学生仿照前面“动脑筋”和“做一做”完成此“做一做”,然后公布如下答案:
2、至此,书中的结论学生已经完全认可了,但要提醒学生认真注意书中结论,把书中有关结论作上记号。
3、书中结论不妨命名为:坐标系中位似变换的判定与性质,这样对结论有更清的认识,更有利于运用解题。
五、对第99页例题的设计思考:
如图3-43,在平面直角坐标系中,已知OABC的顶点坐标分别为O(0,0),A(3,0),B(4,2),C(1,2),以坐标原点O为位似中心,将
OABC放大为原图形的3倍。
在解答此题时,一是要注重对题目的引道分析,帮助学生克服新学知识的生疏性。此题主要是对结论的分析,可设计如下几个问题:
1、此题要画的图形与□ABCD有何关系?
答:位似。
2、位似中心是什么?位拟比是多少?
答:位似中心是坐标原点,位似比是3。
3、怎样得到要画图形的四个顶点的坐标?
答:□OABC各顶点坐标分别乘以3。
二是运用书中结论解答此题后,要认真细致的画图,进一步验证上述结论的正确性,使学生再次感觉结论的真实可靠,从而无形中掌握知识。解答过程如下:
解
将
OABC的各顶点的坐标分别乘3,得A(0,0),A'(9,0),B'(12,6)、C'(3,6),依次连接点O,A'、B'、C',则四边形OA'、B'、C'即为所要求的图形,如图3-44所示。
六、对第99页“练习”的设计思考
1、练习已对本节知识运用的检验,更是让学生发现问题,查漏补缺的良好机会,所以必须给学生充分练习的机会,发现问题的机会。
2、学生参差不齐,初学知识对基础较差学生来说,一时难以运用,要让他们下位去请教。
3、让学生说出答案,学生对自己存在的问题会更加重视。
总之,本节课设计时,老师要强调学生多画图,要认真画图,更要用心画图,要通过画图发现知识,通过画图加深对知识的理解,努力贯彻数形结合的数学教学原则。
2
湖南省教育出版社义务教育教科书《数学》九年级上册第98页到第99页的教学内容,过去湘教版教科书中没有,对于我们来说是新的授课内容,比较生疏,容易忽视,再说,我们的老师上课时不愿意画图,我们的学生更是如此,鉴于此,对本节课的教学设计有以下思考,供广大同行在教学中参考。
一、对本节课的课题设计的思考:
很明显,本节课是在坐标平面中研究位拟变换,因此,命名为“坐标平面中的位似变换”能使学生更加明确本节课的学习目标:
1、如何在坐标平面中进行位拟变换;
2、坐标平面中位似变换时,对应点的坐标与相似比有何关系。
二、对“动脑筋”教学设计的思考:
如图3-40,在平面直角坐标系中,已知△AOB的顶点坐标分别为A(2,4),O(0,0),B(6,0)。
(1)将各个顶点坐标分别扩大为原来的2倍,画出所得到的图形;
(2)以点O为位似中心,分别在线段OA,OB的延长线上取点A′,B′,使==2,依
图
3—40
次连接点A′,O,B′,画出所得到的图形,你发现了什么?
处理此段课文时,老师往往忽视学生动手的必要性,不给学生动手的机会,或学生动手不彻底,从而很难有所发现。不要忘记,实践才能出真知,数学教学中必须时刻遵循的这个原则。
这段课文我建议作如下设计:
1、要求每个学生在图3-40中认真完成(1)将各个顶点坐标分别扩大为原来的2倍,画出所得到的图形。对于基础较差学生,要安排学生辅导完成。
2、要求每个学生在图3-40中认真完成(2)以点O为位似中心,分别在线取OA、OB的延长线上取点A',B',使==2,依次连接A',O,B',画出所得到的图形。对于基础较差学生,要安排学生辅导完成。
3、老师公布参考答案,供个别不会画学生参考:
图3—41
4、请学生思考之后回答(2)你发现了什么?
答:(1)中所画图形与(2)中所画图形是同一个图形。
5、请一个较好的学生回答:对你的发现进一步思考可得出什么结论?
答:顶点坐标扩大2倍所得的三角形与原三角形是位似图形,位似中心是原点,位似比是2。
三、“做一做”的教学设计
如图3-42,在平面直角坐标系中,已知△AOB的顶点坐标分别为A(3,6),O(0,0),B(6,0)。
(1)将各个顶点坐标分别缩小为原来的倍,画出所得到的图形;
图3—42
(2)以点O为位似中心,分别在线段OA,OB的延长线上取点A′,B′,使==,依次连接点A′,O,B′,画出所得到的图形,你发现了什么?
“做一做”是对前面“动脑筋”所得结论的加强和巩固,老师上课时千万不要一跃而过,要确实发挥它的作用。应该要求学生仿效“动脑筋”的步骤进行,只是解决(3)(4)时给基础较差学生机会,让更多学生掌握这节课知识,努力贯彻党的教育方针。
四、对坐标平面中位拟变换的判定与性质的设计思考
1、前面的“动脑筋”、“做一做”的位似图形的位似中心都比较特殊:都是三角形的一个顶点,如果位似中心任取一点,是否有以上结论呢?因此,可设计一个如下“做一做”让全体学生去发现。
如图,在平面直角坐标系中,已知△ABC的顶点坐标分别为A(0,2),B(-1,-1),C(3,1)。
(1)将各个顶点坐标分别扩大成原来的2倍,画出所得图形。
(2)以点O为位似中心,分别在线OA、OB、OC的延长线上取点A'、B'、C',使
=
=
=2
顺次连接A'、B'、C',画出所得到的图形,你发现了什么?
让学生仿照前面“动脑筋”和“做一做”完成此“做一做”,然后公布如下答案:
2、至此,书中的结论学生已经完全认可了,但要提醒学生认真注意书中结论,把书中有关结论作上记号。
3、书中结论不妨命名为:坐标系中位似变换的判定与性质,这样对结论有更清的认识,更有利于运用解题。
五、对第99页例题的设计思考:
如图3-43,在平面直角坐标系中,已知OABC的顶点坐标分别为O(0,0),A(3,0),B(4,2),C(1,2),以坐标原点O为位似中心,将
OABC放大为原图形的3倍。
在解答此题时,一是要注重对题目的引道分析,帮助学生克服新学知识的生疏性。此题主要是对结论的分析,可设计如下几个问题:
1、此题要画的图形与□ABCD有何关系?
答:位似。
2、位似中心是什么?位拟比是多少?
答:位似中心是坐标原点,位似比是3。
3、怎样得到要画图形的四个顶点的坐标?
答:□OABC各顶点坐标分别乘以3。
二是运用书中结论解答此题后,要认真细致的画图,进一步验证上述结论的正确性,使学生再次感觉结论的真实可靠,从而无形中掌握知识。解答过程如下:
解
将
OABC的各顶点的坐标分别乘3,得A(0,0),A'(9,0),B'(12,6)、C'(3,6),依次连接点O,A'、B'、C',则四边形OA'、B'、C'即为所要求的图形,如图3-44所示。
六、对第99页“练习”的设计思考
1、练习已对本节知识运用的检验,更是让学生发现问题,查漏补缺的良好机会,所以必须给学生充分练习的机会,发现问题的机会。
2、学生参差不齐,初学知识对基础较差学生来说,一时难以运用,要让他们下位去请教。
3、让学生说出答案,学生对自己存在的问题会更加重视。
总之,本节课设计时,老师要强调学生多画图,要认真画图,更要用心画图,要通过画图发现知识,通过画图加深对知识的理解,努力贯彻数形结合的数学教学原则。
2
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
