沪科版八年级数学上册第14章全等三角形中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版八年级数学上册第14章全等三角形中考题汇编(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 74.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览


文档简介
沪科版八年级数学上册第八章全等三角形中考题汇编(含答案)
1
一、
选择题
1.
(2019·安顺)如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.
∠A=∠D
B.
AC=DF
C.
AB=ED
D.
BF=EC
2.
(2019·临沂)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是( )
A.
0.5
B.
1
C.
1.5
D.
2
3.
(导学号81760080)(2019·滨州)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.有下列结论:①
AC=BD;②
∠AMB=40°;③
OM平分∠BOC;④
MO平分∠BMC.其中,正确的个数为( )
A.
4
B.
3
C.
2
D.
1
二、
填空题
4.
(2019·上海)在△ABC和△A1B1C1中,∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D,D1分别在边AB,A1B1上,且△ACD≌△C1A1D1,那么AD的长是________.
5.
(2019·齐齐哈尔)如图,在△ABC和△DEF中,∠B=∠E,BF=CE,点B,F,C,E在同一条直线上.若使△ABC≌△DEF,则还需添加的一个条件是________(只填一个即可).
6.
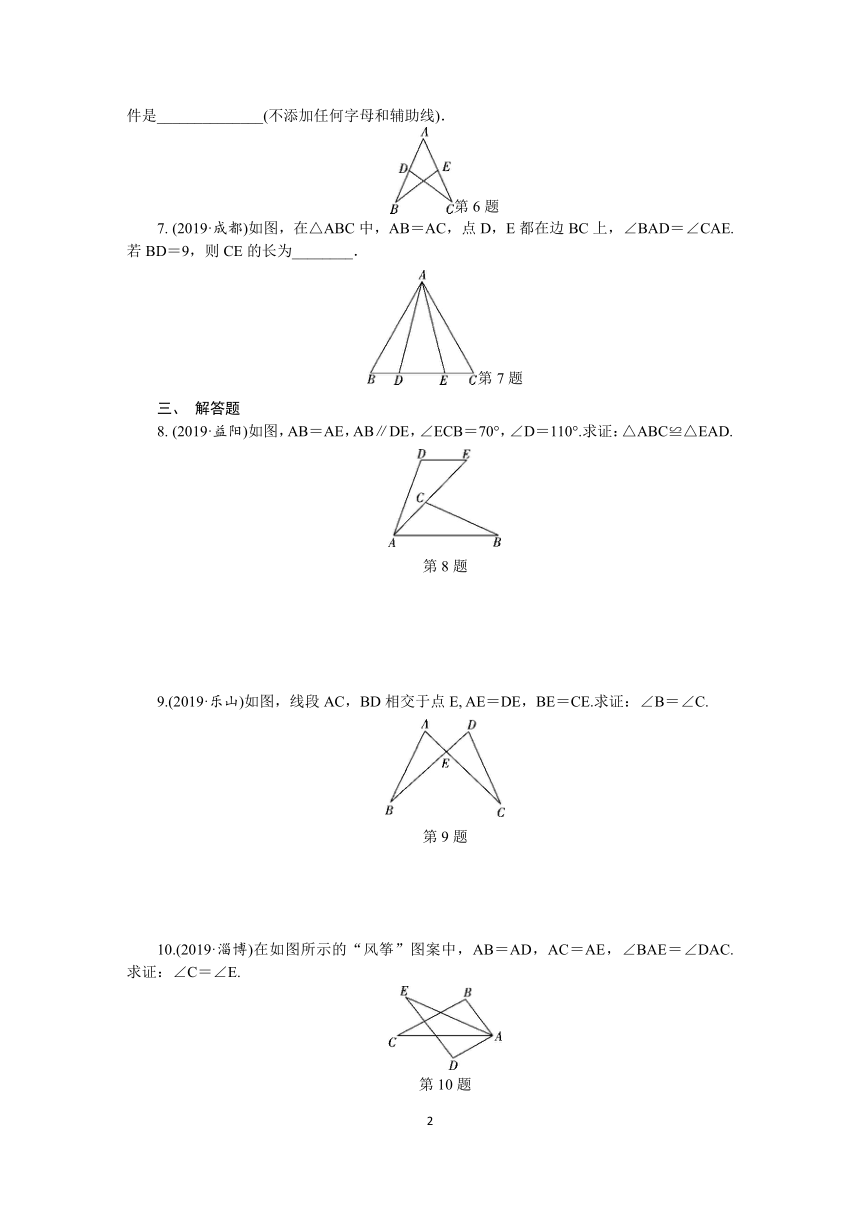
(2019·邵阳)如图,AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是______________(不添加任何字母和辅助线).
7.
(2019·成都)如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE.若BD=9,则CE的长为________.
三、
解答题
8.
(2019·益阳)如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°.求证:△ABC≌△EAD.
第8题
9.(2019·乐山)如图,线段AC,BD相交于点E,
AE=DE,BE=CE.求证:∠B=∠C.
第9题
10.(2019·淄博)在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
第10题
11.(2019·宜昌)如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)
求证:△ABE≌△DBE;
(2)
若∠A=100°,∠C=50°,求∠AEB的度数.
第11题
12.(2019·
苏州)如图,在△ABC中,点E在BC边上,AE=AB.将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)
求证:EF=BC;
(2)
若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
第12题
13.(2019·黄石)如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.求证:
(1)
∠C=∠BAD;
(2)
AC=EF.
第13题
14.(2019·温州)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)
求证:△BDE≌△CDF;
(2)
当AD⊥BC,AE=1,CF=2时,求AC的长.
第14题
15
(2019·安顺)(1)
如图①,在四边形ABCD中,AB∥CD,E是BC的中点.若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB,AD,DC之间的等量关系:________________.
(2)
问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点.若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
参考答案
一、
A
B
B
二、
答案不唯一,如AB=DE
答案不唯一,如AB=AC
9
三、
∵
∠ECB=70°,∴
∠ACB=180°-∠ECB=110°.∵
∠D=110°,∴
∠ACB=∠D.∵
AB∥DE,∴
∠CAB=∠E.又∵
AB=EA,∴
△ABC≌△EAD
在△AEB和△DEC中,∴
△AEB≌△DEC.∴
∠B=∠C
∵
∠BAE=∠DAC,∴
∠BAE+∠CAE=∠DAC+∠CAE.∴
∠CAB=∠EAD.又∵
AB=AD,AC=AE,∴
△ABC≌△ADE.∴
∠C=∠E
(1)
∵
BE平分∠ABC,∴
∠ABE=∠DBE.在△ABE和△DBE中,∴
△ABE≌△DBE (2)
∵
∠A=100°,∠C=50°,∴
∠ABC=180°-100°-50°=30°.∵
BE平分∠ABC,∴
∠ABE=∠ABC=15°.∴
∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°
(1)
∵
线段AC绕点A旋转到AF的位置,∴
AC=AF.∵
∠CAF=∠BAE,∴
∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.在△AEF和△ABC中,∴
△AEF≌△ABC.∴
EF=BC (2)
∵
AE=AB,∴
∠AEB=∠ABC=
65°.∵
△AEF≌△ABC,∴
∠AEF=∠ABC=
65°.∴
∠FEC=180°
-∠AEB-∠AEF=180°-65°-65°=50°.∵
∠FGC是△EGC的外角,∠ACB=28°,∴
∠FGC=∠FEC+∠ACB=50°+28°=78°
(1)
∵
AB=AE,D为线段BE的中点,∴
AD⊥BC.∴
∠C+∠DAC=90°.∵
∠BAC=90°,∴
∠BAD+∠DAC=90°.∴
∠C=∠BAD (2)
∵
AF∥BC,∴
∠FAE=∠AEB.∵
AB=AE,∴
∠B=∠AEB.∴
∠B=∠FAE.∵
EF⊥AE,∴
∠AEF=∠BAC=90°.又∵
AB=EA,∴
△ABC≌△EAF.∴
AC=EF
(1)
∵
CF∥AB,∴
∠EBD=∠FCD,∠BED=∠CFD.∵
AD是BC边上的中线,∴
BD=CD.∴
△BDE≌△CDF (2)
∵
△BDE≌△CDF,∴
BE=CF=2.∴
AB=AE+BE=1+2=3.∵
AD⊥BC,BD=CD,∴
AC=AB=3
(1)
AD=AB+DC (2)
AB=CF+AF.如图,延长AE交DF的延长线于点G.∵
E是BC的中点,∴
CE=BE.∵
AB∥CD,∴
∠BAE=∠G.又∵
BE=CE,∠AEB=∠GEC,∴
△AEB≌△GEC.∴
AB=GC.∵
AE是∠BAF的平分线,∴
∠BAG=∠FAG.∵
∠BAG=∠G,∴
∠FAG=∠G.∴
FA=FG.∵
CG=CF+FG,∴
AB=CF+AF
1
一、
选择题
1.
(2019·安顺)如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.
∠A=∠D
B.
AC=DF
C.
AB=ED
D.
BF=EC
2.
(2019·临沂)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是( )
A.
0.5
B.
1
C.
1.5
D.
2
3.
(导学号81760080)(2019·滨州)如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.有下列结论:①
AC=BD;②
∠AMB=40°;③
OM平分∠BOC;④
MO平分∠BMC.其中,正确的个数为( )
A.
4
B.
3
C.
2
D.
1
二、
填空题
4.
(2019·上海)在△ABC和△A1B1C1中,∠C=∠C1=90°,AC=A1C1=3,BC=4,B1C1=2,点D,D1分别在边AB,A1B1上,且△ACD≌△C1A1D1,那么AD的长是________.
5.
(2019·齐齐哈尔)如图,在△ABC和△DEF中,∠B=∠E,BF=CE,点B,F,C,E在同一条直线上.若使△ABC≌△DEF,则还需添加的一个条件是________(只填一个即可).
6.
(2019·邵阳)如图,AD=AE,请你添加一个条件,使得△ADC≌△AEB,你添加的条件是______________(不添加任何字母和辅助线).
7.
(2019·成都)如图,在△ABC中,AB=AC,点D,E都在边BC上,∠BAD=∠CAE.若BD=9,则CE的长为________.
三、
解答题
8.
(2019·益阳)如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°.求证:△ABC≌△EAD.
第8题
9.(2019·乐山)如图,线段AC,BD相交于点E,
AE=DE,BE=CE.求证:∠B=∠C.
第9题
10.(2019·淄博)在如图所示的“风筝”图案中,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
第10题
11.(2019·宜昌)如图,在△ABC中,D是BC边上的一点,AB=DB,BE平分∠ABC,交AC边于点E,连接DE.
(1)
求证:△ABE≌△DBE;
(2)
若∠A=100°,∠C=50°,求∠AEB的度数.
第11题
12.(2019·
苏州)如图,在△ABC中,点E在BC边上,AE=AB.将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,EF与AC交于点G.
(1)
求证:EF=BC;
(2)
若∠ABC=65°,∠ACB=28°,求∠FGC的度数.
第12题
13.(2019·黄石)如图,在△ABC中,∠BAC=90°,E为边BC上的点,且AB=AE,D为线段BE的中点,过点E作EF⊥AE,过点A作AF∥BC,且AF,EF相交于点F.求证:
(1)
∠C=∠BAD;
(2)
AC=EF.
第13题
14.(2019·温州)如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
(1)
求证:△BDE≌△CDF;
(2)
当AD⊥BC,AE=1,CF=2时,求AC的长.
第14题
15
(2019·安顺)(1)
如图①,在四边形ABCD中,AB∥CD,E是BC的中点.若AE是∠BAD的平分线,试判断AB,AD,DC之间的等量关系.
解决此问题可以用如下方法:延长AE交DC的延长线于点F,易证△AEB≌△FEC,得到AB=FC,从而把AB,AD,DC转化在一个三角形中即可判断.
AB,AD,DC之间的等量关系:________________.
(2)
问题探究:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点.若AE是∠BAF的平分线,试探究AB,AF,CF之间的等量关系,并证明你的结论.
参考答案
一、
A
B
B
二、
答案不唯一,如AB=DE
答案不唯一,如AB=AC
9
三、
∵
∠ECB=70°,∴
∠ACB=180°-∠ECB=110°.∵
∠D=110°,∴
∠ACB=∠D.∵
AB∥DE,∴
∠CAB=∠E.又∵
AB=EA,∴
△ABC≌△EAD
在△AEB和△DEC中,∴
△AEB≌△DEC.∴
∠B=∠C
∵
∠BAE=∠DAC,∴
∠BAE+∠CAE=∠DAC+∠CAE.∴
∠CAB=∠EAD.又∵
AB=AD,AC=AE,∴
△ABC≌△ADE.∴
∠C=∠E
(1)
∵
BE平分∠ABC,∴
∠ABE=∠DBE.在△ABE和△DBE中,∴
△ABE≌△DBE (2)
∵
∠A=100°,∠C=50°,∴
∠ABC=180°-100°-50°=30°.∵
BE平分∠ABC,∴
∠ABE=∠ABC=15°.∴
∠AEB=180°-∠A-∠ABE=180°-100°-15°=65°
(1)
∵
线段AC绕点A旋转到AF的位置,∴
AC=AF.∵
∠CAF=∠BAE,∴
∠CAF+∠CAE=∠BAE+∠CAE,即∠EAF=∠BAC.在△AEF和△ABC中,∴
△AEF≌△ABC.∴
EF=BC (2)
∵
AE=AB,∴
∠AEB=∠ABC=
65°.∵
△AEF≌△ABC,∴
∠AEF=∠ABC=
65°.∴
∠FEC=180°
-∠AEB-∠AEF=180°-65°-65°=50°.∵
∠FGC是△EGC的外角,∠ACB=28°,∴
∠FGC=∠FEC+∠ACB=50°+28°=78°
(1)
∵
AB=AE,D为线段BE的中点,∴
AD⊥BC.∴
∠C+∠DAC=90°.∵
∠BAC=90°,∴
∠BAD+∠DAC=90°.∴
∠C=∠BAD (2)
∵
AF∥BC,∴
∠FAE=∠AEB.∵
AB=AE,∴
∠B=∠AEB.∴
∠B=∠FAE.∵
EF⊥AE,∴
∠AEF=∠BAC=90°.又∵
AB=EA,∴
△ABC≌△EAF.∴
AC=EF
(1)
∵
CF∥AB,∴
∠EBD=∠FCD,∠BED=∠CFD.∵
AD是BC边上的中线,∴
BD=CD.∴
△BDE≌△CDF (2)
∵
△BDE≌△CDF,∴
BE=CF=2.∴
AB=AE+BE=1+2=3.∵
AD⊥BC,BD=CD,∴
AC=AB=3
(1)
AD=AB+DC (2)
AB=CF+AF.如图,延长AE交DF的延长线于点G.∵
E是BC的中点,∴
CE=BE.∵
AB∥CD,∴
∠BAE=∠G.又∵
BE=CE,∠AEB=∠GEC,∴
△AEB≌△GEC.∴
AB=GC.∵
AE是∠BAF的平分线,∴
∠BAG=∠FAG.∵
∠BAG=∠G,∴
∠FAG=∠G.∴
FA=FG.∵
CG=CF+FG,∴
AB=CF+AF
