华东师大版九年级数学下册 第26章 二次函数 单元测试题(Word版 含解析)
文档属性
| 名称 | 华东师大版九年级数学下册 第26章 二次函数 单元测试题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 143.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-10 00:00:00 | ||
图片预览



文档简介
第26章
二次函数
单元测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列函数是二次函数的是(?
?
?
?
)
A.
B.
C.
D.
?
2.
已知正方形,设,则正方形的面积与之间的函数关系式为(
)
A.
B.
C.
D.
?
3.
与
的图象的不同之处是(????????)
A.对称轴
B.开口方向
C.顶点
D.形状
?
4.
对抛物线:而言,下列结论正确的是(
)
A.与轴有两个交点
B.开口向上
C.与轴的交点坐标是
D.顶点坐标是
?
5.
抛物线的顶点坐标一定位于
(?
?
?
?
)
A.轴的负半轴上
B.第二象限
C.第三象限
D.第二象限或第三象限
?
6.
二次函数的顶点坐标是?
?
?
?
A.
B.
C.
D.
?
7.
对于二次函数,下列说法错误的是?
?
?
?
A.对称轴为直线
B.其图象一定经过点
C.当时,随的增大而增大
D.当时,将抛物线先向上平移个单位,再向左平移个单位,得到抛物线.
?
8.
已知二次函数,当时,随的增大而增大,当时,随的增大而减小,当时,的值为(?
?
?
?
)
A.
B.
C.
D.
?
9.
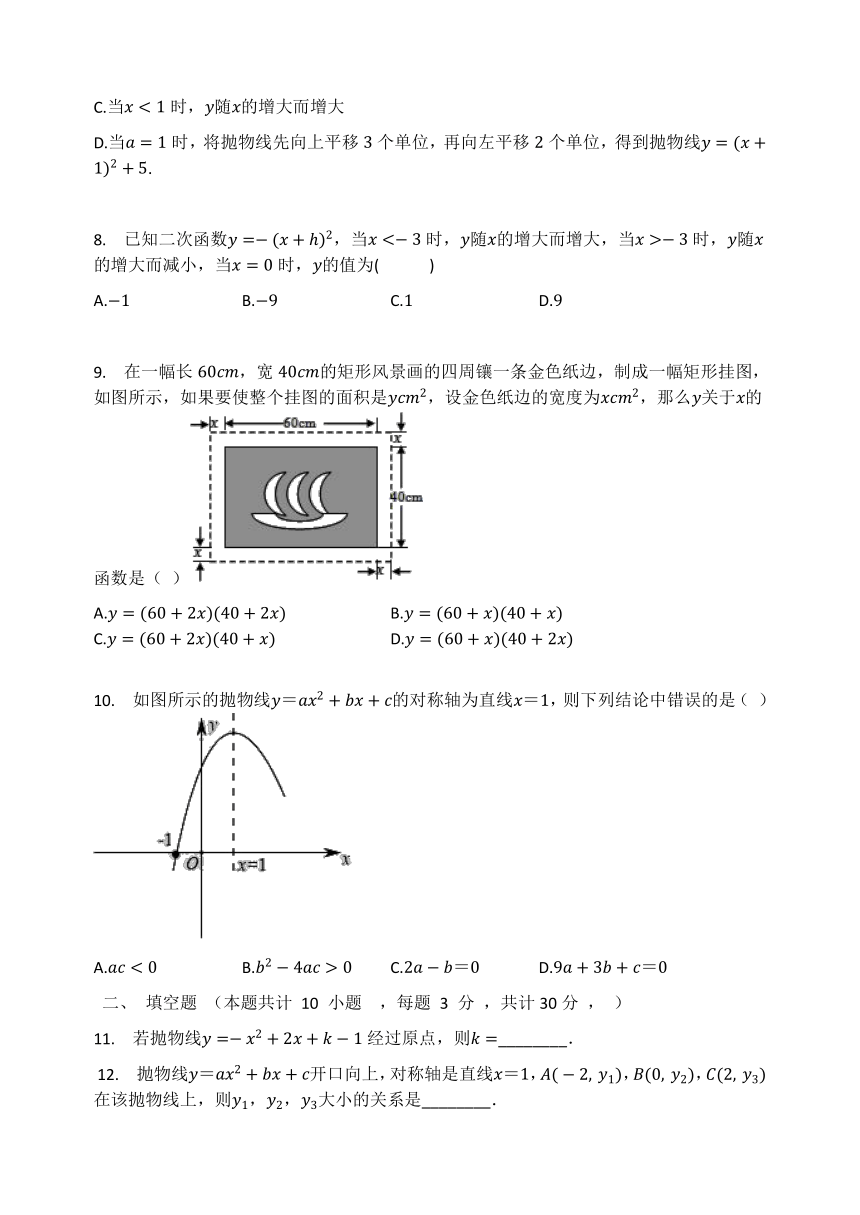
在一幅长,宽的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是,设金色纸边的宽度为,那么关于的函数是(
)
A.
B.
C.
D.
?
10.
如图所示的抛物线=的对称轴为直线=,则下列结论中错误的是(
)
A.
B.
C.=
D.=
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
若抛物线经过原点,则________.
?12.
抛物线=开口向上,对称轴是直线=,,,在该抛物线上,则,,大小的关系是________.
?
13.
将二次函数的图象绕着它与轴的交点旋转所得到新抛物线表达式为________.
?
14.
将抛物线向下平移,若平移后的抛物线经过点,则平移后的抛物线的解析式为________.
?
15.
抛物线的对称轴是直线,那么抛物线的解析式是________.
?
16.
已知抛物线的顶点坐标为,且过点,则该抛物线的表达式为________.
?
17.
已知,点,,都在函数的图象上,则,,的大小关系是________.
?
18.
把二次函数化成的形式是________.
?
19.
有一种产品的质量要求从低到高分为,,,共四种不同的档次.若工时不变,车间每天可生产最低档次(即第一档次)的产品件,生产每件产品的利润为元;如果每提高一个档次,每件产品利润可增加元,但每天少生产件产品.现在车间计划只生产一种档次的产品.要使利润最大,车间应生产第________种档次的产品.
?
20.
已知二次函数的图象如图所示,则这个二次函数的表达式是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知二次函数和函数.
(1)你能用图象法求出方程的解吗?试试看;
(2)请通过解方程的方法验证(1)问的解.
?
22.
抛物线与轴交于,,与轴交于,且
(1)求,的坐标;
(2)到,,距离相等,在抛物线上求点,使,,,为顶点的四边形为平行四边形.
?
23.
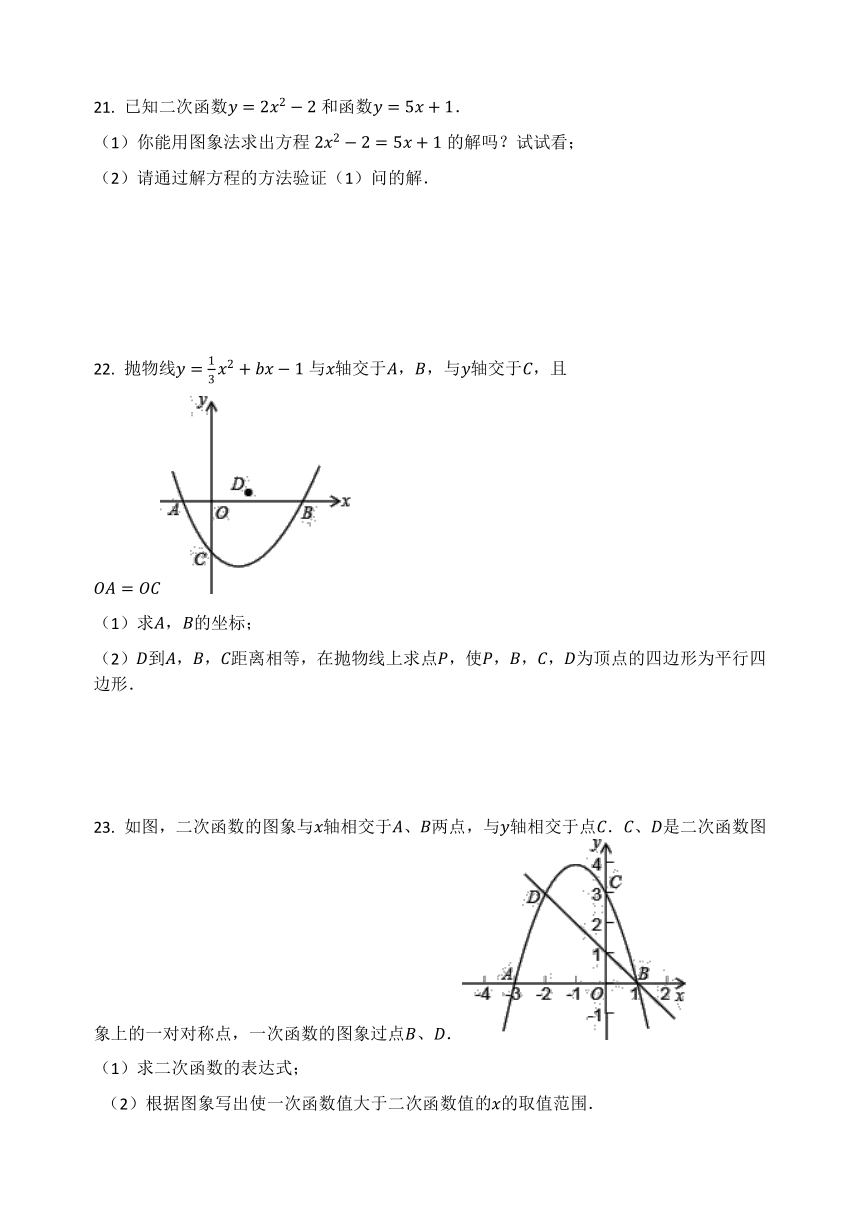
如图,二次函数的图象与轴相交于、两点,与轴相交于点.、是二次函数图象上的一对对称点,一次函数的图象过点、.
(1)求二次函数的表达式;
(2)根据图象写出使一次函数值大于二次函数值的的取值范围.
?
24.
某商场购进一批换季衣服,进价为每件元.市场调研发现,以单价元出售,平均月销售量为件.在此基础上,若单价每降低元,则平均月销售量增加件.
(1)商场想要这种衣服平均月销售量至少件,那么单价至多为多少元?
(2)当单价定为多少元时,商场卖这批衣服的月销售利润达到最大?最大月销售利润为多少元?
?
25.
某商场要经营一种新上市的文具,进价为元/件,试营销阶段发现;当销售单价元/件时,每天的销售量是件,销售单价每上涨元,每天的销售量就减少件.
(1)写出商场销售这种文具,每天所得的销售利润(元)与销售单价(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?
?
26.
如图,在平面直角坐标系中,抛物线与轴的交点为点和点,与轴的交点为,对称轴是,对称轴与轴交于点.
(1)求抛物线的函数表达式;
(2)点为对称轴上一个动点,当的值最小时,求点的坐标;
(3)在第一象限内的抛物线上是否存在点,使得?若存在,直接写出点的坐标;若不存在,请说明理由.
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:,是二次函数;
,,是一次函数;
,,不是含自变量的整式,不是二次函数;
,,二次项系数不能确定是否为,不是二次函数.
故选.
2.
【答案】
B
【解答】
解:由正方形面积公式得:
.
故选.
3.
【答案】
C
【解答】
解:函数的对称轴是轴,开口向上,顶点;
函数的对称轴是轴,开口向上,顶点;
这两个函数的二次项系数都是,则它们的形状相同.
故选.
4.
【答案】
D
【解答】
解:,∵
,抛物线与轴无交点,本选项错误;
,∵
二次项系数,抛物线开口向下,本选项错误;
,当时,,抛物线与轴交点坐标为,本选项错误;
,∵
,∴
抛物线顶点坐标为,本选项正确.
故选.
5.
【答案】
B
【解答】
此题暂无解答
6.
【答案】
C
【解答】
解:∵
∴
抛物线顶点坐标为,
故选.
7.
【答案】
C
【解答】
解:、对称轴为直线,正确;
、当时,,正确;
、当时,,将抛物线先向上平移个单位,
再向左平移个单位,得到抛物线,正确.
故选.
8.
【答案】
B
【解答】
解:由题意得:二次函数的对称轴为,
故,
把代入二次函数可得,
当时,.
故选.
9.
【答案】
A
【解答】
解:长是:,宽是:,
由矩形的面积公式得
则.
故选.
10.
【答案】
【解答】
解:、由抛物线可知,
.故正确;
、…二次函数的图象与轴有两个交点,
∴
即
…故正确;
、由对称轴可知,
∴
,故错误;
、关于的对称点为
…当时,,故正确;
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:把代入得,解得.
故答案为.
12.
【答案】
=
【解答】
∵
抛物线=开口向上,对称轴是直线=,
∴
抛物线上的点离对称轴越远,对应的函数值就越大,
∵
取时所对应的点离对称轴最远,取与时所对应的点离对称轴一样近,
∴
=.
13.
【答案】
【解答】
解:因为二次函数的图象绕它与轴的交点旋转后,其对称轴不变,只是图象开口向下,因此二次函数新抛物线表达式为
故答案为:.
14.
【答案】
【解答】
解:设平移后抛物线的表达式为,
把代入,得
,
解得.
所以平移后的抛物线的解析式是.
故答案为:.
15.
【答案】
【解答】
解:∵
抛物线的对称轴是直线,
∴
,
解得:,
∴
,
故答案为:.
16.
【答案】
.
【解答】
解:设函数的解析式是.
把代入函数解析式得,
解得:,
则抛物线的解析式是.
17.
【答案】
【解答】
解:∵
当时,,
而抛物线的对称轴为直线,开口向上,
∴
三点都在对称轴的左边,随的增大而减小,
∴
.
故本题答案为:.
18.
【答案】
【解答】
解:.
故答案为.
19.
【答案】
【解答】
解:设生产档的产品.
利润,
∴
时,利润最大为,
故答案为.
20.
【答案】
【解答】
解:根据图象可知顶点坐标,
设函数解析式是:,
把点代入解析式,得:
,即,
∴
解析式为,即.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:(1)如图在平面直角坐标系内画出和函数的图象,
图象交点的横坐标是,
的解是,;
(2)化简得
,
因式分解,得.
解得,.
【解答】
解:(1)如图在平面直角坐标系内画出和函数的图象,
图象交点的横坐标是,
的解是,;
(2)化简得
,
因式分解,得.
解得,.
22.
【答案】
解:(1)∵
抛物线与轴交于,,与轴交于,且,
∴
,
∴
的坐标,,
代入得,解得,,
∴
抛物线为,
令,则,解得,,,
∴
的坐标为.
(2)如图,∵
到,,距离相等,
∴
是直线和的交点,
∴
,
∵
使,,,为顶点的四边形为平行四边形,,,
∴
,,.
∴
当的坐标为或或时,使,,,为顶点的四边形为平行四边形.
【解答】
解:(1)∵
抛物线与轴交于,,与轴交于,且,
∴
,
∴
的坐标,,
代入得,解得,,
∴
抛物线为,
令,则,解得,,,
∴
的坐标为.
(2)如图,∵
到,,距离相等,
∴
是直线和的交点,
∴
,
∵
使,,,为顶点的四边形为平行四边形,,,
∴
,,.
∴
当的坐标为或或时,使,,,为顶点的四边形为平行四边形.
23.
【答案】
解:(1)设抛物线的解析式为,由函数图象,得
,
解得:,
,
.
∴
二次函数的表达式为:;
(2)设直线的解析式为,由直线经过和,得
,
解得:,
一次函数的解析式为:.
,
解得:,
故抛物线与轴的加点坐标为:或.
由函数图象得:当或时,一次函数值大于二次函数值.
【解答】
解:(1)设抛物线的解析式为,由函数图象,得
,
解得:,
,
.
∴
二次函数的表达式为:;
(2)设直线的解析式为,由直线经过和,得
,
解得:,
一次函数的解析式为:.
,
解得:,
故抛物线与轴的加点坐标为:或.
由函数图象得:当或时,一次函数值大于二次函数值.
24.
【答案】
解;(1)设单价定为元,
,
解得,
即单价至少为元;
(2)设单价定为元,销售利润为元,
,
∴
时,取得最大值,此时,
即当单价定为元时,商场卖这批衣服的月销售利润达到最大,最大月销售利润为元.
【解答】
解;(1)设单价定为元,
,
解得,
即单价至少为元;
(2)设单价定为元,销售利润为元,
,
∴
时,取得最大值,此时,
即当单价定为元时,商场卖这批衣服的月销售利润达到最大,最大月销售利润为元.
25.
【答案】
解:(1)由题意可得:
;
(2)∵
,
∴
当时,取到最大值,
即销售单价为元时,每天销售利润最大,最大利润为元.
【解答】
解:(1)由题意可得:
;
(2)∵
,
∴
当时,取到最大值,
即销售单价为元时,每天销售利润最大,最大利润为元.
26.
【答案】
解:(1)∵
抛物线交轴于,
∴
,
∵
对称轴是,
∴
,即,
两关于、的方程联立解得?,,
∴
抛物线为.
(2)由得到:,
如图,点关于对称轴对称的点的坐标为:.连接交于点,此时的值最小.
设直线方程为:,
则,
解得.
故直线的方程为:.
当时,,
所以;
(3)∵
,,
∴
.
如果,那么,
∵
在轴上,
∴
为或.
①当为时,连接,过作直线平分交于,交抛物线于,,连接、,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得,
∴
.
设,则有,
解得,或,
则,.
②当为时,连接,过作直线平分交于,交抛物线于,,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得?,
∴
.
设,则有,
解得或,
则,.
综上所述,点的坐标为或或或.
【解答】
解:(1)∵
抛物线交轴于,
∴
,
∵
对称轴是,
∴
,即,
两关于、的方程联立解得?,,
∴
抛物线为.
(2)由得到:,
如图,点关于对称轴对称的点的坐标为:.连接交于点,此时的值最小.
设直线方程为:,
则,
解得.
故直线的方程为:.
当时,,
所以;
(3)∵
,,
∴
.
如果,那么,
∵
在轴上,
∴
为或.
①当为时,连接,过作直线平分交于,交抛物线于,,连接、,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得,
∴
.
设,则有,
解得,或,
则,.
②当为时,连接,过作直线平分交于,交抛物线于,,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得?,
∴
.
设,则有,
解得或,
则,.
综上所述,点的坐标为或或或.
二次函数
单元测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
下列函数是二次函数的是(?
?
?
?
)
A.
B.
C.
D.
?
2.
已知正方形,设,则正方形的面积与之间的函数关系式为(
)
A.
B.
C.
D.
?
3.
与
的图象的不同之处是(????????)
A.对称轴
B.开口方向
C.顶点
D.形状
?
4.
对抛物线:而言,下列结论正确的是(
)
A.与轴有两个交点
B.开口向上
C.与轴的交点坐标是
D.顶点坐标是
?
5.
抛物线的顶点坐标一定位于
(?
?
?
?
)
A.轴的负半轴上
B.第二象限
C.第三象限
D.第二象限或第三象限
?
6.
二次函数的顶点坐标是?
?
?
?
A.
B.
C.
D.
?
7.
对于二次函数,下列说法错误的是?
?
?
?
A.对称轴为直线
B.其图象一定经过点
C.当时,随的增大而增大
D.当时,将抛物线先向上平移个单位,再向左平移个单位,得到抛物线.
?
8.
已知二次函数,当时,随的增大而增大,当时,随的增大而减小,当时,的值为(?
?
?
?
)
A.
B.
C.
D.
?
9.
在一幅长,宽的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是,设金色纸边的宽度为,那么关于的函数是(
)
A.
B.
C.
D.
?
10.
如图所示的抛物线=的对称轴为直线=,则下列结论中错误的是(
)
A.
B.
C.=
D.=
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?
11.
若抛物线经过原点,则________.
?12.
抛物线=开口向上,对称轴是直线=,,,在该抛物线上,则,,大小的关系是________.
?
13.
将二次函数的图象绕着它与轴的交点旋转所得到新抛物线表达式为________.
?
14.
将抛物线向下平移,若平移后的抛物线经过点,则平移后的抛物线的解析式为________.
?
15.
抛物线的对称轴是直线,那么抛物线的解析式是________.
?
16.
已知抛物线的顶点坐标为,且过点,则该抛物线的表达式为________.
?
17.
已知,点,,都在函数的图象上,则,,的大小关系是________.
?
18.
把二次函数化成的形式是________.
?
19.
有一种产品的质量要求从低到高分为,,,共四种不同的档次.若工时不变,车间每天可生产最低档次(即第一档次)的产品件,生产每件产品的利润为元;如果每提高一个档次,每件产品利润可增加元,但每天少生产件产品.现在车间计划只生产一种档次的产品.要使利润最大,车间应生产第________种档次的产品.
?
20.
已知二次函数的图象如图所示,则这个二次函数的表达式是________.
三、
解答题
(本题共计
6
小题
,共计60分
,
)
?
21.
已知二次函数和函数.
(1)你能用图象法求出方程的解吗?试试看;
(2)请通过解方程的方法验证(1)问的解.
?
22.
抛物线与轴交于,,与轴交于,且
(1)求,的坐标;
(2)到,,距离相等,在抛物线上求点,使,,,为顶点的四边形为平行四边形.
?
23.
如图,二次函数的图象与轴相交于、两点,与轴相交于点.、是二次函数图象上的一对对称点,一次函数的图象过点、.
(1)求二次函数的表达式;
(2)根据图象写出使一次函数值大于二次函数值的的取值范围.
?
24.
某商场购进一批换季衣服,进价为每件元.市场调研发现,以单价元出售,平均月销售量为件.在此基础上,若单价每降低元,则平均月销售量增加件.
(1)商场想要这种衣服平均月销售量至少件,那么单价至多为多少元?
(2)当单价定为多少元时,商场卖这批衣服的月销售利润达到最大?最大月销售利润为多少元?
?
25.
某商场要经营一种新上市的文具,进价为元/件,试营销阶段发现;当销售单价元/件时,每天的销售量是件,销售单价每上涨元,每天的销售量就减少件.
(1)写出商场销售这种文具,每天所得的销售利润(元)与销售单价(元)之间的函数关系式;
(2)求销售单价为多少元时,该文具每天的销售利润最大?最大利润是多少?
?
26.
如图,在平面直角坐标系中,抛物线与轴的交点为点和点,与轴的交点为,对称轴是,对称轴与轴交于点.
(1)求抛物线的函数表达式;
(2)点为对称轴上一个动点,当的值最小时,求点的坐标;
(3)在第一象限内的抛物线上是否存在点,使得?若存在,直接写出点的坐标;若不存在,请说明理由.
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:,是二次函数;
,,是一次函数;
,,不是含自变量的整式,不是二次函数;
,,二次项系数不能确定是否为,不是二次函数.
故选.
2.
【答案】
B
【解答】
解:由正方形面积公式得:
.
故选.
3.
【答案】
C
【解答】
解:函数的对称轴是轴,开口向上,顶点;
函数的对称轴是轴,开口向上,顶点;
这两个函数的二次项系数都是,则它们的形状相同.
故选.
4.
【答案】
D
【解答】
解:,∵
,抛物线与轴无交点,本选项错误;
,∵
二次项系数,抛物线开口向下,本选项错误;
,当时,,抛物线与轴交点坐标为,本选项错误;
,∵
,∴
抛物线顶点坐标为,本选项正确.
故选.
5.
【答案】
B
【解答】
此题暂无解答
6.
【答案】
C
【解答】
解:∵
∴
抛物线顶点坐标为,
故选.
7.
【答案】
C
【解答】
解:、对称轴为直线,正确;
、当时,,正确;
、当时,,将抛物线先向上平移个单位,
再向左平移个单位,得到抛物线,正确.
故选.
8.
【答案】
B
【解答】
解:由题意得:二次函数的对称轴为,
故,
把代入二次函数可得,
当时,.
故选.
9.
【答案】
A
【解答】
解:长是:,宽是:,
由矩形的面积公式得
则.
故选.
10.
【答案】
【解答】
解:、由抛物线可知,
.故正确;
、…二次函数的图象与轴有两个交点,
∴
即
…故正确;
、由对称轴可知,
∴
,故错误;
、关于的对称点为
…当时,,故正确;
故选:.
二、
填空题
(本题共计
10
小题
,每题
3
分
,共计30分
)
11.
【答案】
【解答】
解:把代入得,解得.
故答案为.
12.
【答案】
=
【解答】
∵
抛物线=开口向上,对称轴是直线=,
∴
抛物线上的点离对称轴越远,对应的函数值就越大,
∵
取时所对应的点离对称轴最远,取与时所对应的点离对称轴一样近,
∴
=.
13.
【答案】
【解答】
解:因为二次函数的图象绕它与轴的交点旋转后,其对称轴不变,只是图象开口向下,因此二次函数新抛物线表达式为
故答案为:.
14.
【答案】
【解答】
解:设平移后抛物线的表达式为,
把代入,得
,
解得.
所以平移后的抛物线的解析式是.
故答案为:.
15.
【答案】
【解答】
解:∵
抛物线的对称轴是直线,
∴
,
解得:,
∴
,
故答案为:.
16.
【答案】
.
【解答】
解:设函数的解析式是.
把代入函数解析式得,
解得:,
则抛物线的解析式是.
17.
【答案】
【解答】
解:∵
当时,,
而抛物线的对称轴为直线,开口向上,
∴
三点都在对称轴的左边,随的增大而减小,
∴
.
故本题答案为:.
18.
【答案】
【解答】
解:.
故答案为.
19.
【答案】
【解答】
解:设生产档的产品.
利润,
∴
时,利润最大为,
故答案为.
20.
【答案】
【解答】
解:根据图象可知顶点坐标,
设函数解析式是:,
把点代入解析式,得:
,即,
∴
解析式为,即.
三、
解答题
(本题共计
6
小题
,每题
10
分
,共计60分
)
21.
【答案】
解:(1)如图在平面直角坐标系内画出和函数的图象,
图象交点的横坐标是,
的解是,;
(2)化简得
,
因式分解,得.
解得,.
【解答】
解:(1)如图在平面直角坐标系内画出和函数的图象,
图象交点的横坐标是,
的解是,;
(2)化简得
,
因式分解,得.
解得,.
22.
【答案】
解:(1)∵
抛物线与轴交于,,与轴交于,且,
∴
,
∴
的坐标,,
代入得,解得,,
∴
抛物线为,
令,则,解得,,,
∴
的坐标为.
(2)如图,∵
到,,距离相等,
∴
是直线和的交点,
∴
,
∵
使,,,为顶点的四边形为平行四边形,,,
∴
,,.
∴
当的坐标为或或时,使,,,为顶点的四边形为平行四边形.
【解答】
解:(1)∵
抛物线与轴交于,,与轴交于,且,
∴
,
∴
的坐标,,
代入得,解得,,
∴
抛物线为,
令,则,解得,,,
∴
的坐标为.
(2)如图,∵
到,,距离相等,
∴
是直线和的交点,
∴
,
∵
使,,,为顶点的四边形为平行四边形,,,
∴
,,.
∴
当的坐标为或或时,使,,,为顶点的四边形为平行四边形.
23.
【答案】
解:(1)设抛物线的解析式为,由函数图象,得
,
解得:,
,
.
∴
二次函数的表达式为:;
(2)设直线的解析式为,由直线经过和,得
,
解得:,
一次函数的解析式为:.
,
解得:,
故抛物线与轴的加点坐标为:或.
由函数图象得:当或时,一次函数值大于二次函数值.
【解答】
解:(1)设抛物线的解析式为,由函数图象,得
,
解得:,
,
.
∴
二次函数的表达式为:;
(2)设直线的解析式为,由直线经过和,得
,
解得:,
一次函数的解析式为:.
,
解得:,
故抛物线与轴的加点坐标为:或.
由函数图象得:当或时,一次函数值大于二次函数值.
24.
【答案】
解;(1)设单价定为元,
,
解得,
即单价至少为元;
(2)设单价定为元,销售利润为元,
,
∴
时,取得最大值,此时,
即当单价定为元时,商场卖这批衣服的月销售利润达到最大,最大月销售利润为元.
【解答】
解;(1)设单价定为元,
,
解得,
即单价至少为元;
(2)设单价定为元,销售利润为元,
,
∴
时,取得最大值,此时,
即当单价定为元时,商场卖这批衣服的月销售利润达到最大,最大月销售利润为元.
25.
【答案】
解:(1)由题意可得:
;
(2)∵
,
∴
当时,取到最大值,
即销售单价为元时,每天销售利润最大,最大利润为元.
【解答】
解:(1)由题意可得:
;
(2)∵
,
∴
当时,取到最大值,
即销售单价为元时,每天销售利润最大,最大利润为元.
26.
【答案】
解:(1)∵
抛物线交轴于,
∴
,
∵
对称轴是,
∴
,即,
两关于、的方程联立解得?,,
∴
抛物线为.
(2)由得到:,
如图,点关于对称轴对称的点的坐标为:.连接交于点,此时的值最小.
设直线方程为:,
则,
解得.
故直线的方程为:.
当时,,
所以;
(3)∵
,,
∴
.
如果,那么,
∵
在轴上,
∴
为或.
①当为时,连接,过作直线平分交于,交抛物线于,,连接、,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得,
∴
.
设,则有,
解得,或,
则,.
②当为时,连接,过作直线平分交于,交抛物线于,,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得?,
∴
.
设,则有,
解得或,
则,.
综上所述,点的坐标为或或或.
【解答】
解:(1)∵
抛物线交轴于,
∴
,
∵
对称轴是,
∴
,即,
两关于、的方程联立解得?,,
∴
抛物线为.
(2)由得到:,
如图,点关于对称轴对称的点的坐标为:.连接交于点,此时的值最小.
设直线方程为:,
则,
解得.
故直线的方程为:.
当时,,
所以;
(3)∵
,,
∴
.
如果,那么,
∵
在轴上,
∴
为或.
①当为时,连接,过作直线平分交于,交抛物线于,,连接、,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得,
∴
.
设,则有,
解得,或,
则,.
②当为时,连接,过作直线平分交于,交抛物线于,,如图所示,
此时,,
∵
,
∴
为的中点,即,
设过,的直线为,则,
解得?,
∴
.
设,则有,
解得或,
则,.
综上所述,点的坐标为或或或.
