沪科版八年级数学上册>第12章一次函数的图象和性质中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版八年级数学上册>第12章一次函数的图象和性质中考题汇编(Word版 含答案) | 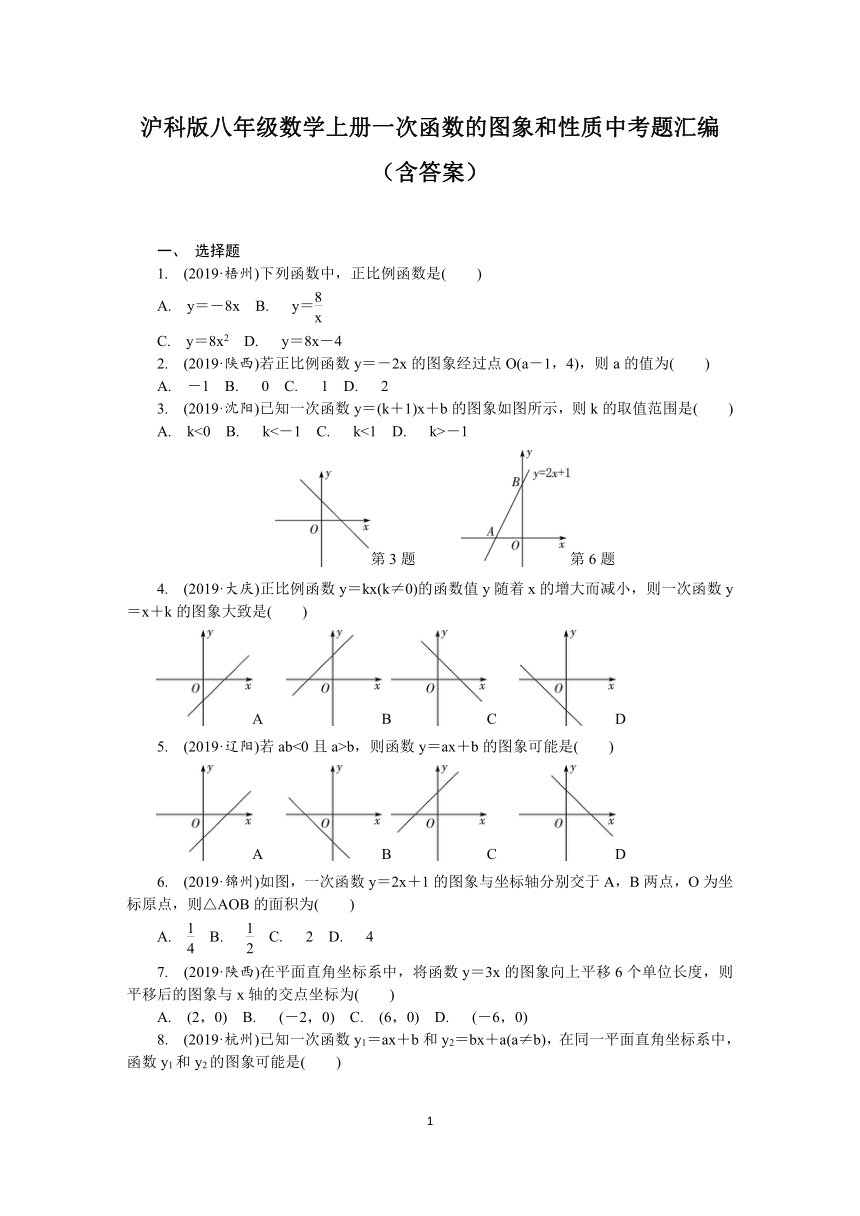 | |
| 格式 | zip | ||
| 文件大小 | 182.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 18:20:02 | ||
图片预览


文档简介
沪科版八年级数学上册一次函数的图象和性质中考题汇编(含答案)
1
一、
选择题
1.
(2019·梧州)下列函数中,正比例函数是( )
A.
y=-8x
B.
y=
C.
y=8x2
D.
y=8x-4
2.
(2019·陕西)若正比例函数y=-2x的图象经过点O(a-1,4),则a的值为( )
A.
-1
B.
0
C.
1
D.
2
3.
(2019·沈阳)已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是( )
A.
k<0
B.
k<-1
C.
k<1
D.
k>-1
4.
(2019·大庆)正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,则一次函数y=x+k的图象大致是( )
5.
(2019·辽阳)若ab<0且a>b,则函数y=ax+b的图象可能是( )
6.
(2019·锦州)如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为( )
A.
B.
C.
2
D.
4
7.
(2019·陕西)在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )
A.
(2,0)
B.
(-2,0)
C.
(6,0)
D.
(-6,0)
8.
(2019·杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),在同一平面直角坐标系中,函数y1和y2的图象可能是( )
9.
(2019·娄底)如图,直线y=x+b和y=kx+2与x轴分别交于点A(-2,0),点B(3,0),则解集为( )
A.
x<-2
B.
x>3
C.
x<-2或x>3
D.
-210.
(2019·苏州)若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.
x<0
B.
x>0
C.
x<1
D.
x>1
11.
(2019·通辽)如图,直线y=kx+b(k≠0)经过点(-1,3),则不等式kx+b≥3的解集为( )
A.
x>-1
B.
x<-1
C.
x≥3
D.
x≥-1
12.
(2019·遵义)如图,直线l1:y=x+6与直线l2:y=-x-2交于点P(-2,3),不等式x+6>-x-2的解集是( )
A.
x>-2
B.
x≥-2
C.
x<-2
D.
x≤-2
13.
(2019·桂林)如图,四边形ABCD的顶点坐标分别为A(-4,0),B(-2,-1),C(3,0),D(0,3),当过点B的直线l将四边形ABCD分成面积相等的两部分时,直线l对应的函数解析式为( )
A.
y=x+
B.
y=x+
C.
y=x+1
D.
y=x+
二、
填空题
14.
(2018·阿坝州)若一次函数y=kx-2的函数值y随自变量x的增大而减小,则k的取值范围是________.
15.
(2019·成都)已知一次函数y=(k-3)x+1的图象经过第一、二、四象限,则k的取值范围是________.
16.
(2019·天津)直线y=2x-1与x轴的交点坐标为________.
17.
(2019·湘潭)将一次函数y=3x的图象向上平移2个单位长度,所得图象对应的函数解析式为________.
18.
(2019·黔东南州)如图,一次函数y=ax+b(a,b为常数,且a>0)的图象经过点A(4,1),则不等式ax+b<1的解集为________.
19.
(2019·无锡)已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为________.
20.
(2019·烟台)如图,直线y=x+2与直线y=ax+c相交于点P(m,3),则关于x的不等式x+2≤ax+c的解集为________.
21.
(2019·鄂州)在平面直角坐标系中,点P(x0,y0)到直线Ax+By+C=0的距离公式为d=,则点P(3,-3)到直线y=-x+的距离为________.
22.
(2019·盐城)如图,在平面直角坐标系中,一次函数y=2x-1的图象分别交x轴,y轴于点A,B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC对应的函数解析式是________.
三、
解答题
23.
(2019·潍坊)当直线y=(2-2k)x+k-3经过第二、三、四象限时,求k的取值范围.
24.(2019·南京)已知一次函数y1=kx+2(k为常数,k≠0)和y2=x-3.
(1)
当k=-2时,若y1>y2,求x的取值范围.
(2)
当x<1时,y1>y2.结合图象,直接写出k的取值范围.
25.(2019·江西)如图,在平面直角坐标系中,点A,B的坐标分别为,,连接AB,以AB为边向上作等边三角形ABC.求:
(1)
点C的坐标.
(2)
线段BC所在直线对应的函数解析式.
第25题
26.(2019·北京)在平面直角坐标系xOy中,直线l:y=kx+1(k≠0)与直线x=k,直线y=-k分别交于点A,B,直线x=k与直线y=-k交于点C.
(1)
求直线l与y轴的交点坐标.
(2)
已知横、纵坐标都是整数的点叫整点,记线段AB,BC,CA围成的区域(不含边界)为W.
①
当k=2时,结合函数图象,求区域W内的整点个数;
②
若区域W内没有整点,直接写出k的取值范围.
参考答案
一、
A
A
B
A
A
A
B
A
D
D
D
A
D
二、
k<0
k<3
y=3x+2
x<4
x<2
x≤1
y=x-1
三、
∵
直线y=(2-2k)x+k-3经过第二、三、四象限,∴
解得1<k<3
(1)
k=-2时,y1=-2x+2.根据题意,得-2x+2>x-3,解得x< (2)
-4≤k≤1且k≠0
(1)
如图,过点B作BH⊥x轴于点H,∵
点A的坐标为,点B的坐标为,∴
AH=-=,BH=1.∴
AB==2.∵
BH=1,∴
在Rt△ABH中,∠BAH=30°.∵
△ABC为等边三角形,∴
AB=AC=2,∠CAB=60°.∴
∠CAB+∠BAH=90°.∴
点C的纵坐标为2.∴
点C的坐标为 (2)
由(1),知点C的坐标为,点B的坐标为.设线段BC所在直线对应的函数解析式为y=kx+b,则解得∴
线段BC所在直线对应的函数解析式为y=-x+
(1)
令x=0,得y=1.∴
直线l与y轴的交点坐标为(0,1)
(2)
由题意,得A(k,k2+1),B,C(k,-k).①
当k=2时,A(2,5),B,C(2,-2),结合图象(图略),易得在区域W内有6个整数点 ②
-1≤k<0或k=-2
1
一、
选择题
1.
(2019·梧州)下列函数中,正比例函数是( )
A.
y=-8x
B.
y=
C.
y=8x2
D.
y=8x-4
2.
(2019·陕西)若正比例函数y=-2x的图象经过点O(a-1,4),则a的值为( )
A.
-1
B.
0
C.
1
D.
2
3.
(2019·沈阳)已知一次函数y=(k+1)x+b的图象如图所示,则k的取值范围是( )
A.
k<0
B.
k<-1
C.
k<1
D.
k>-1
4.
(2019·大庆)正比例函数y=kx(k≠0)的函数值y随着x的增大而减小,则一次函数y=x+k的图象大致是( )
5.
(2019·辽阳)若ab<0且a>b,则函数y=ax+b的图象可能是( )
6.
(2019·锦州)如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为( )
A.
B.
C.
2
D.
4
7.
(2019·陕西)在平面直角坐标系中,将函数y=3x的图象向上平移6个单位长度,则平移后的图象与x轴的交点坐标为( )
A.
(2,0)
B.
(-2,0)
C.
(6,0)
D.
(-6,0)
8.
(2019·杭州)已知一次函数y1=ax+b和y2=bx+a(a≠b),在同一平面直角坐标系中,函数y1和y2的图象可能是( )
9.
(2019·娄底)如图,直线y=x+b和y=kx+2与x轴分别交于点A(-2,0),点B(3,0),则解集为( )
A.
x<-2
B.
x>3
C.
x<-2或x>3
D.
-2
(2019·苏州)若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点A(0,-1),B(1,1),则不等式kx+b>1的解集为( )
A.
x<0
B.
x>0
C.
x<1
D.
x>1
11.
(2019·通辽)如图,直线y=kx+b(k≠0)经过点(-1,3),则不等式kx+b≥3的解集为( )
A.
x>-1
B.
x<-1
C.
x≥3
D.
x≥-1
12.
(2019·遵义)如图,直线l1:y=x+6与直线l2:y=-x-2交于点P(-2,3),不等式x+6>-x-2的解集是( )
A.
x>-2
B.
x≥-2
C.
x<-2
D.
x≤-2
13.
(2019·桂林)如图,四边形ABCD的顶点坐标分别为A(-4,0),B(-2,-1),C(3,0),D(0,3),当过点B的直线l将四边形ABCD分成面积相等的两部分时,直线l对应的函数解析式为( )
A.
y=x+
B.
y=x+
C.
y=x+1
D.
y=x+
二、
填空题
14.
(2018·阿坝州)若一次函数y=kx-2的函数值y随自变量x的增大而减小,则k的取值范围是________.
15.
(2019·成都)已知一次函数y=(k-3)x+1的图象经过第一、二、四象限,则k的取值范围是________.
16.
(2019·天津)直线y=2x-1与x轴的交点坐标为________.
17.
(2019·湘潭)将一次函数y=3x的图象向上平移2个单位长度,所得图象对应的函数解析式为________.
18.
(2019·黔东南州)如图,一次函数y=ax+b(a,b为常数,且a>0)的图象经过点A(4,1),则不等式ax+b<1的解集为________.
19.
(2019·无锡)已知一次函数y=kx+b的图象如图所示,则关于x的不等式3kx-b>0的解集为________.
20.
(2019·烟台)如图,直线y=x+2与直线y=ax+c相交于点P(m,3),则关于x的不等式x+2≤ax+c的解集为________.
21.
(2019·鄂州)在平面直角坐标系中,点P(x0,y0)到直线Ax+By+C=0的距离公式为d=,则点P(3,-3)到直线y=-x+的距离为________.
22.
(2019·盐城)如图,在平面直角坐标系中,一次函数y=2x-1的图象分别交x轴,y轴于点A,B,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC对应的函数解析式是________.
三、
解答题
23.
(2019·潍坊)当直线y=(2-2k)x+k-3经过第二、三、四象限时,求k的取值范围.
24.(2019·南京)已知一次函数y1=kx+2(k为常数,k≠0)和y2=x-3.
(1)
当k=-2时,若y1>y2,求x的取值范围.
(2)
当x<1时,y1>y2.结合图象,直接写出k的取值范围.
25.(2019·江西)如图,在平面直角坐标系中,点A,B的坐标分别为,,连接AB,以AB为边向上作等边三角形ABC.求:
(1)
点C的坐标.
(2)
线段BC所在直线对应的函数解析式.
第25题
26.(2019·北京)在平面直角坐标系xOy中,直线l:y=kx+1(k≠0)与直线x=k,直线y=-k分别交于点A,B,直线x=k与直线y=-k交于点C.
(1)
求直线l与y轴的交点坐标.
(2)
已知横、纵坐标都是整数的点叫整点,记线段AB,BC,CA围成的区域(不含边界)为W.
①
当k=2时,结合函数图象,求区域W内的整点个数;
②
若区域W内没有整点,直接写出k的取值范围.
参考答案
一、
A
A
B
A
A
A
B
A
D
D
D
A
D
二、
k<0
k<3
y=3x+2
x<4
x<2
x≤1
y=x-1
三、
∵
直线y=(2-2k)x+k-3经过第二、三、四象限,∴
解得1<k<3
(1)
k=-2时,y1=-2x+2.根据题意,得-2x+2>x-3,解得x< (2)
-4≤k≤1且k≠0
(1)
如图,过点B作BH⊥x轴于点H,∵
点A的坐标为,点B的坐标为,∴
AH=-=,BH=1.∴
AB==2.∵
BH=1,∴
在Rt△ABH中,∠BAH=30°.∵
△ABC为等边三角形,∴
AB=AC=2,∠CAB=60°.∴
∠CAB+∠BAH=90°.∴
点C的纵坐标为2.∴
点C的坐标为 (2)
由(1),知点C的坐标为,点B的坐标为.设线段BC所在直线对应的函数解析式为y=kx+b,则解得∴
线段BC所在直线对应的函数解析式为y=-x+
(1)
令x=0,得y=1.∴
直线l与y轴的交点坐标为(0,1)
(2)
由题意,得A(k,k2+1),B,C(k,-k).①
当k=2时,A(2,5),B,C(2,-2),结合图象(图略),易得在区域W内有6个整数点 ②
-1≤k<0或k=-2
