沪科版九年级数学上册21.5 反比例函数的图象、性质及其应用中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版九年级数学上册21.5 反比例函数的图象、性质及其应用中考题汇编(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 440.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览


文档简介
沪科版九年级数学上册反比例函数的图象、性质及其应用中考题汇编(含答案)
17
一、
选择题
1.
(2019·孝感)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1
200
N和0.5
m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A.
F=
B.
F=
C.
F=
D.
F=
2.
(2019·上海)下列函数中,函数值y随自变量x的值增大而增大的是( )
A.
y=
B.
y=-
C.
y=
D.
y=-
3.
(2019·柳州)反比例函数y=的图象位于( )
A.
第一、三象限
B.
第二、三象限
C.
第一、二象限
D.
第二、四象限
4.
(2019·淮安)当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是( )
5.
(2019·江西)已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下列说法正确的是
( )
A.
反比例函数y2的解析式是y2=-
B.
两个函数图象的另一交点坐标为(2,-4)
C.
当x<-2或0<x<2时,y1<y2
D.
正比例函数y1与反比例函数y2都随x的增大而增大
6.
(2019·安徽)已知点A(1,-3)关于x轴的对称点A′在反比例函数y=的图象上,则实数k的值为( )
A.
3
B.
C.
-3
D.
-
7.
(2019·哈尔滨)点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.
(4,-1)
B.
C.
(-4,-1)
D.
8.
(2019·毕节)若点A(-4,y1),B(-2,y2),C(2,y3)都在反比例函数y=-的图象上,则y1,y2,y3的大小关系是( )
A.
y1>y2>y3
B.
y3>y2>y1
C.
y2>y1>y3
D.
y1>y3>y2
9.
(2019·崇左)若点(-1,y1),(2,y2),(3,y3)在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系是( )
A.
y1>y2>y3
B.
y3>y2>y1
C.
y1>y3>y2
D.
y2>y3>y1
10.
(2019·徐州)若A(x1,y1),B(x2,y2)都在函数y=的图象上,且x1<0<x2,则( )
A.
y1<y2
B.
y1=y2
C.
y1>y2
D.
y1=-y2
11.
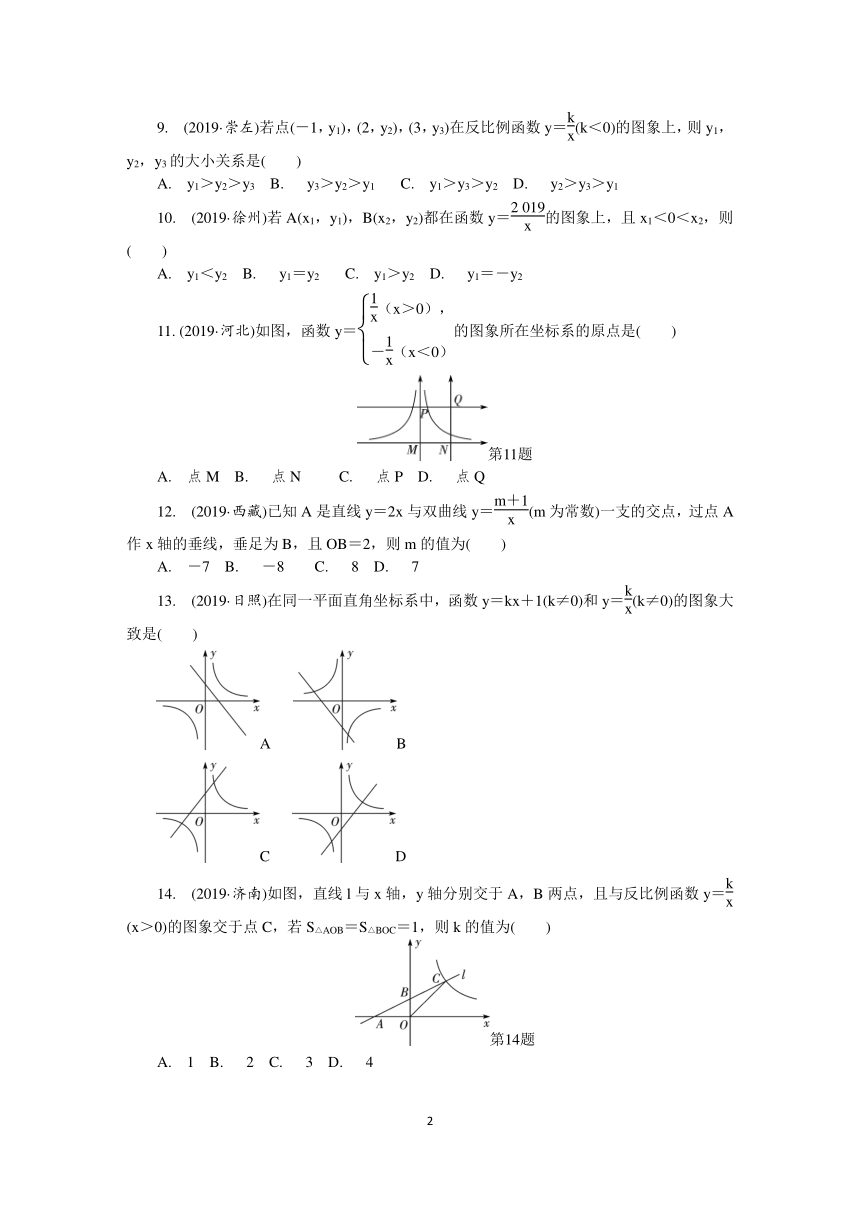
(2019·河北)如图,函数y=的图象所在坐标系的原点是( )
A.
点M
B.
点N
C.
点P
D.
点Q
12.
(2019·西藏)已知A是直线y=2x与双曲线y=(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,且OB=2,则m的值为( )
A.
-7
B.
-8
C.
8
D.
7
13.
(2019·日照)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
14.
(2019·济南)如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k的值为( )
A.
1
B.
2
C.
3
D.
4
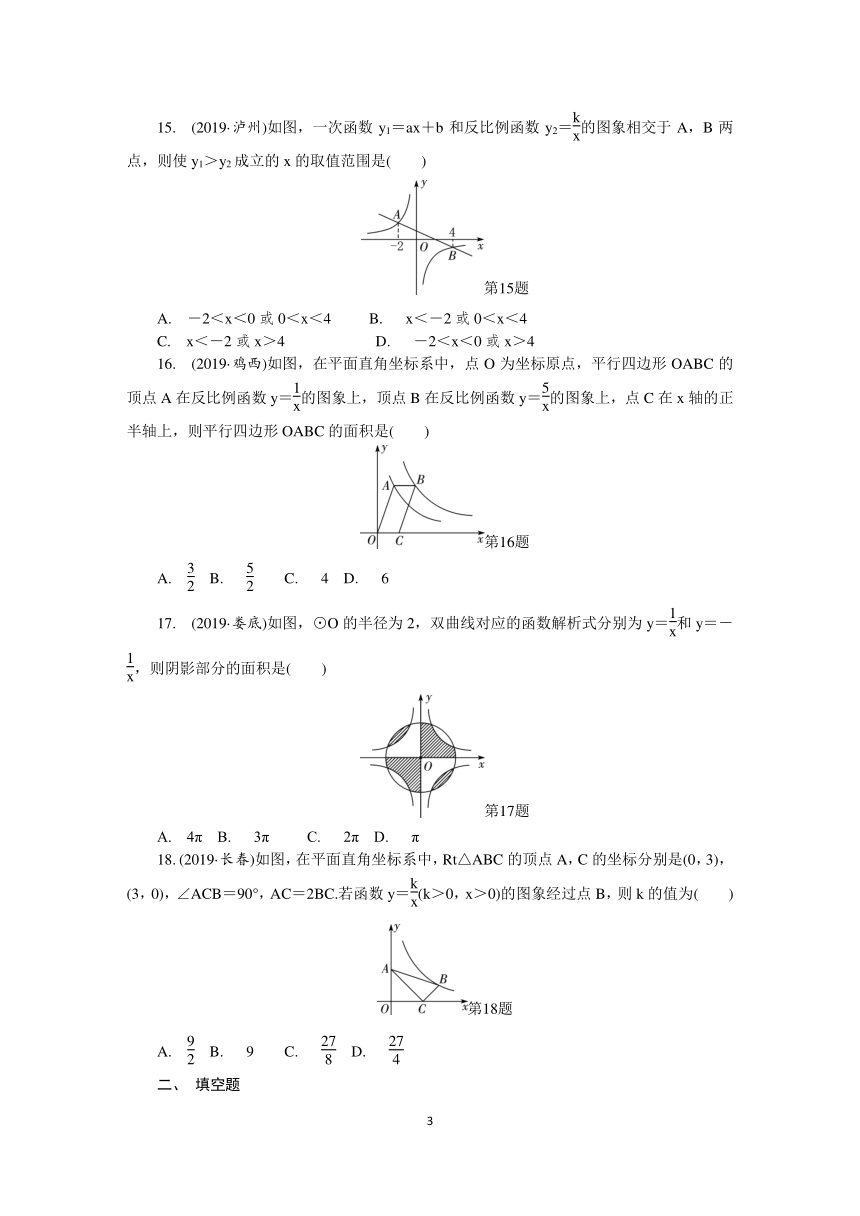
15.
(2019·泸州)如图,一次函数y1=ax+b和反比例函数y2=的图象相交于A,B两点,则使y1>y2成立的x的取值范围是( )
A.
-2<x<0或0<x<4
B.
x<-2或0<x<4
C.
x<-2或x>4
D.
-2<x<0或x>4
16.
(2019·鸡西)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A.
B.
C.
4
D.
6
17.
(2019·娄底)如图,⊙O的半径为2,双曲线对应的函数解析式分别为y=和y=-,则阴影部分的面积是( )
A.
4π
B.
3π
C.
2π
D.
π
18.
(2019·长春)如图,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,3),(3,0),∠ACB=90°,AC=2BC.若函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A.
B.
9
C.
D.
二、
填空题
19.
(2019·云南)若点(3,5)在反比例函数y=(k≠0)的图象上,则k=________.
20.
(2019·镇江)若已知点A(-2,y1),B(-1,y2)都在反比例函数y=-的图象上,则y1________y2(填“>”或“<”
).
21.
(2019·山西)如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A的坐标为(-4,0),点D的坐标为(-1,4),反比例函数y=(x>0)的图象恰好经过点C,则k的值为________.
22.
(2019·绥化)一次函数y1=-x+6与反比例函数y2=(x>0)的图象如图所示,当y1>y2时,自变量x的取值范围是________.
23.
(2019·青海)如图,P是反比例函数y=图象上的一点,过点P向x轴作垂线,垂足为A,连接OP.若图中涂色部分的面积是1,则此反比例函数的解析式为________.
24.
(2019·安顺)如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于A,B两点,连接OA,OB,已知△OAB的面积为4,则k1-k2=________.
25.
(2019·北京)在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为________.
26.
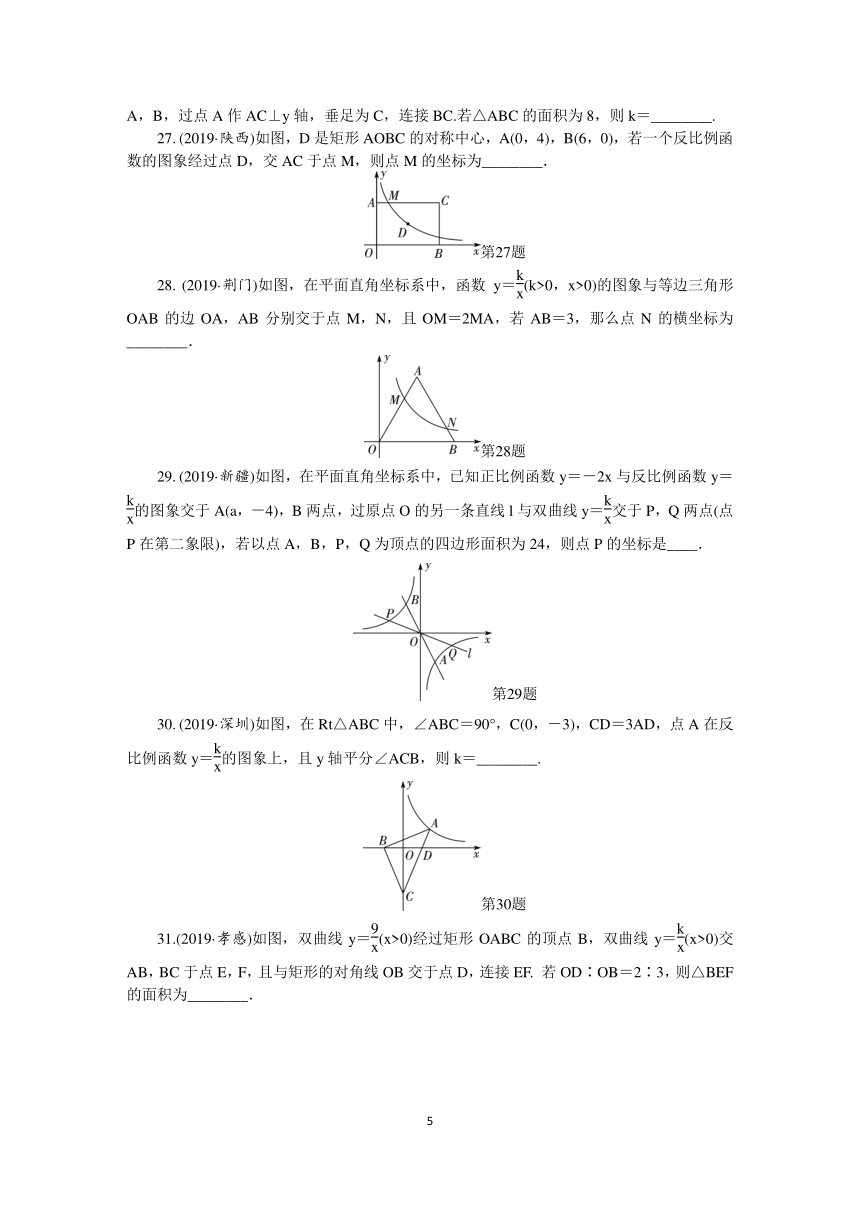
(2019·黄冈)如图,一直线经过原点O,且与反比例函数y=(k>0)的图象相交于点A,B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC的面积为8,则k=________.
27.
(2019·陕西)如图,D是矩形AOBC的对称中心,A(0,4),B(6,0),若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为________.
28.
(2019·荆门)如图,在平面直角坐标系中,函数y=(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM=2MA,若AB=3,那么点N的横坐标为________.
29.
(2019·新疆)如图,在平面直角坐标系中,已知正比例函数y=-2x与反比例函数y=的图象交于A(a,-4),B两点,过原点O的另一条直线l与双曲线y=交于P,Q两点(点P在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是____.
30.
(2019·深圳)如图,在Rt△ABC中,∠ABC=90°,C(0,-3),CD=3AD,点A在反比例函数y=的图象上,且y轴平分∠ACB,则k=________.
31.(2019·孝感)如图,双曲线y=(x>0)经过矩形OABC的顶点B,双曲线y=(x>0)交AB,BC于点E,F,且与矩形的对角线OB交于点D,连接EF.
若OD∶OB=2∶3,则△BEF的面积为________.
32.
(2019·南通)如图,过点C(3,4)的直线y=2x+b交x轴于点A,∠ABC=90°,AB=CB,曲线y=(x>0)过点B,将点A沿y轴正方向平移a个单位长度恰好落在该曲线上,则a的值为________.
三、
解答题
33.
(2019·常州)如图,在?OABC中,OA=2,∠AOC=45°,点C在y轴上,D是BC的中点,反比例函数y=(x>0)的图象经过点A,D.求:
(1)
k的值;
(2)
点D的坐标.
第33题
34.(2019·盐城)如图,一次函数y=x+1的图象交y轴于点A,与反比例函数y=(x>0)的图象交于点B(m,2).求:
(1)
反比例函数的解析式;
(2)
△AOB的面积.
第34题
35.(2019·宿迁)如图,一次函数y=kx+b的图象与反比例函数y=-的图象相交于A(-1,m),B(n,-1)两点.求:
(1)
一次函数的解析式;
(2)
△AOB的面积.
第35题
36.(2019·东营)如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a),B两点,BC⊥x轴,垂足为C,△AOC的面积是2.求:
(1)
m,n的值;
(2)
直线AC对应的函数解析式.
第36题
37.(2019·广东)如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A,B两点,其中点A的坐标为(-1,4),点B的坐标为(4,n).
(1)
根据图象,直接写出满足k1x+b>的x的取值范围;
(2)
求这两个函数的解析式;
(3)
点P在线段AB上,且S△AOP∶S△BOP=1∶2,求点P的坐标.
第37题
38.
(2019·葫芦岛)如图,一次函数y=k1x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y=的图象分别交于C,D两点,点C的坐标为(2,4),B是线段AC的中点.
(1)
求一次函数y=k1x+b与反比例函数y=的解析式;
(2)
求△COD的面积;
(3)
直接写出当x取什么值时,k1x+b<.
第38题
39.(2019·大庆)如图,反比例函数y=和一次函数y=kx-1的图象相交于A(m,2m),B两点.
(1)
求一次函数的解析式;
(2)
求出点B的坐标,并根据图象直接写出满足不等式<kx-1的x的取值范围.
第39题
40.(2019·湘西州)如图,一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
(1)
求函数y=和y=kx+b的解析式;
(2)
结合图象直接写出不等式组0<<kx+b的解集.
第40题
41.
(2019·襄阳)如图,一次函数y1=kx+b与反比例函数y2=的图象在第一、三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)
求一次函数和反比例函数的解析式;
(2)
比较大小:AD________BC(填“>”“<”或“=”);
(3)
直接写出y1<y2时,x的取值范围.
第41题
42.
(2019·大连)如图,在平面直角坐标系xOy中,点A(3,2)在反比例函数y=(x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.
(1)
求该反比例函数的解析式;
(2)
若S△ACD=,设点C的坐标为(a,0),求线段BD的长.
第42题
43.(2019·雅安)如图,在平面直角坐标系中,一次函数y=-x+m的图象与反比例函数y=(x>0)的图象交于A,B两点,已知A(2,4).
(1)
求一次函数和反比例函数的解析式;
(2)
求点B的坐标;
(3)
连接AO,BO,求△AOB的面积.
第43题
44.
((2019·成都)如图,在平面直角坐标系xOy中,一次函数y=x+5和y=-2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)
求反比例函数的解析式;
(2)
设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积.
第44题
45.(2018·河南)小明在研究矩形面积S与矩形的边长x,y之间的关系时,得到如下数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
4
3
2
■
1
0.5
结果发现一个数据被墨水涂黑了.
(1)
被墨水涂黑的数据为________.
(2)
y与x之间的函数解析式为________,且y随x的增大而________.
(3)
如图是小明画出的y关于x的函数图象,点B,E均在该函数的图象上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1和S2的大小关系,并说明理由.
(4)
在(3)的条件下,DE交BC于点G,反比例函数y=的图象经过点G,交AB于点H,连接OG,OH,则四边形OGBH的面积为________.
第45题
46.(2019·杭州)方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480
km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定为不超过120
km/h.
(1)
求v关于t的函数解析式;
(2)
方方上午8点驾驶小汽车从A地出发.
①
方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②
方方能否在当天11点30分前到达B地?说明理由.
47.(2018·乐山)某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y
(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)
求y与x(0≤x≤24)的函数解析式;
(2)
求恒温系统设定的恒定温度;
(3)
若大棚内的温度低于10
℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多长时间,才能使蔬菜避免受到伤害?
第47题
48.
(2019·鄂尔多斯)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10
℃,加热到100
℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30
℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30
℃时接通电源,水温y(℃)与时间x(min)的关系如图所示.
(1)
分别写出水温上升和下降阶段y与x之间的函数解析式;
(2)
怡萱同学想喝高于50
℃的水,请问她最多需要等待多长时间?
第48题
参考答案
一、
B
A
A
B
C
A
A
C
C
A
A
D
C
D
B
C
C
D
二、
15
<
16
2y=
8
0
8
(-4,2)或(-1,8)
4
三、
(1)
过点A作AH⊥y轴于点H.在Rt△AOH中,∵
∠AOC=45°,OA=2,∴
OH=AH=2.∴
点A的坐标为(2,2).∴
k=4 (2)
∵
四边形OABC是平行四边形,∴
OC∥AB.∴
AB⊥x轴.∴
点B的横坐标为2.∵
D是BC的中点,∴
点D的横坐标为1.又由(1),知反比例函数的解析式为y=,且点D在其图象上,∴
点D的坐标为(1,4)
(1)
∵
点B(m,2)在一次函数y=x+1的图象上,∴
2=m+1,解得m=1.∴
点B的坐标为(1,2).∵
点B(1,2)在反比例函数y=(x>0)的图象上,∴
k=2×1=2,即反比例函数的解析式是y= (2)
将x=0代入y=x+1,得y=1,则点A的坐标为(0,1).∵
点B的坐标为(1,2),∴
S△AOB=×1×1=
(1)
把A(-1,m),B(n,-1)分别代入y=-,得m=5,n=5,∴
点A的坐标为(-1,5),点B的坐标为(5,-1).把A(-1,5),B(5,-1)代入y=kx+b,得解得∴
一次函数的解析式为y=-x+4 (2)
如图,当x=0时,y=4,∴
OD=4.∴
S△AOB=S△AOD+S△BOD=×4×1+×4×5=12
(1)
∵
直线y=mx与双曲线y=相交于A(-2,a),B两点,∴
点A与点B关于原点成中心对称.∴
点B的坐标为(2,-a).∴
点C的坐标为(2,0).∴
OC=2.∵
S△AOC=2,∴
×2a=2,解得a=2.∴
点A的坐标为(-2,2).把A(-2,2)代入y=mx和y=,得解得 (2)
设直线AC对应的函数解析式为y=kx+b,∵
直线经过点A,C,∴
解得∴
直线AC对应的函数解析式为y=-x+1
(1)
x<-1或0<x<4 (2)
∵
反比例函数y=的图象过点A(-1,4),B(4,n),∴
k2=-1×4=-4,k2=4n.∴
n=-1.∴
点B的坐标为(4,-1).∵
一次函数y=k1x+b的图象过点A,B,∴
解得∴
一次函数的解析式为y=-x+3,反比例函数的解析式为y=- (3)
设直线AB与y轴的交点为C,则点C的坐标为(0,3).∴
S△AOB=S△AOC+S△BOC=×3×1+×3×4=.∵
S△AOP∶S△BOP=1∶2,∴
S△AOP=×=.∴
S△COP=S△AOP-S△AOC=-=1.∴
×3·xP=1.∴
xP=.∵
点P在线段AB上,∴
y=.∴
点P的坐标为
(1)
∵
点C(2,4)在反比例函数y=的图象上,∴
k2=2×4=8.∴
反比例函数的解析式为y=.如图,过点C作CE⊥x轴于点E,∵
C(2,4),B是线段AC的中点,∴
易得点B的坐标为(0,2).∵
B,C两点在一次函数y=k1x+b的图象上,∴
解得∴
一次函数的解析式为y=x+2
(2)
由解得或∴
点D的坐标为(-4,-2).∴
S△COD=S△BOC+S△BOD=×2×2+×2×4=6 (3)
由图象,可得当0<x<2或x<-4时,k1x+b<
(1)
∵
A(m,2m)在反比例函数y=的图象上,∴
2m=.∴
m=1.∴
点A的坐标为(1,2).又∵
点A(1,2)在一次函数y=kx-1的图象上,∴
2=k-1,即k=3.∴
一次函数的解析式为y=3x-1 (2)
联立解得或∴
点B的坐标为.由图象,知满足不等式<kx-1的x的取值范围为-<x<0或x>1
(1)
把点A(3,2)代入反比例函数y=,可得m=3×2=6,∴
反比例函数的解析式为y=.∵
OB=4,∴
点B的坐标为(0,-4).把点A(3,2),B(0,-4)代入一次函数y=kx+b,可得解得∴
一次函数的解析式为y=2x-4
(2)
x>3
(1)
把A(3,4)代入反比例函数y2=,得4=,解得m=12.∴
反比例函数的解析式为y2=.∵
点B(a,-2)在反比例函数y2=的图象上,∴
-2a=12,解得a=-6.∴
点B的坐标为(-6,-2).∵
一次函数y1=kx+b的图象经过A(3,4),B(-6,-2)两点,∴
解得∴
一次函数的解析式为y1=x+2 (2)
= (3)
由图象,可知当y1<y2时,x的取值范围是x<-6或0<x<3
(1)
∵
点A(3,2)在反比例函数y=(x>0)的图象上,∴
k=3×2=6.∴
反比例函数的解析式为y= (2)
如图,过点A作AE⊥OC,垂足为E,设直线OA对应的函数解析式为y=mx,将A(3,2)代入,得2=3m,解得m=.∴
直线OA对应的函数解析式为y=x.∵
点C的坐标为(a,0),BC⊥x轴,把x=a代入y=x,得y=a,∴
点B的坐标为.∴
BC=a.把x=a代入y=,得y=.∴
点D的坐标为.∴
CD=.∵
S△ACD=,∴
CD·EC=,即··(a-3)=,解得a=6.∴
BD=BC-CD=a-=3
(1)
将A(2,4)代入y=-x+m与y=(x>0)中,得4=-2+m,4=,∴
m=6,k=8.∴
一次函数的解析式为y=-x+6,反比例函数的解析式为y= (2)
联立解得或∴
点B的坐标为(4,2) (3)
设直线y=-x+6与y轴交于点C,易得点C的坐标为(0,6),∴
OC=6.∴
易得S△AOB=S△COB-S△AOC=×6×4-×6×2=6
(1)
由解得∴
点A的坐标为(-2,4).∵
反比例函数y=的图象经过点A,∴
k=-2×4=-8.∴
反比例函数的解析式是y=- (2)
联立解得或∴
点B的坐标为(-8,1).∵
直线AB对应的函数解析式为y=x+5,∴
易得直线AB与x轴的交点坐标为(-10,0).∴
S△ABO=×10×4-×10×1=15
(1)
1.5 (2)
y= 减小 (3)
S1=S2 理由:∵
S1=OA·AB=6,S2=OD·DE=6,∴
S1=S2. (4)
4
(1)
∵
vt=480,且全程速度限定为不超过120
km/h,∴
v关于t的函数解析式为v=(t≥4) (2)
①
8点至12点48分的时长为
h,8点至14点的时长为6
h,将t=6代入v=,得v=80;将t=代入v=,得v=100.∴
小汽车行驶速度v的范围为80≤v≤100 ②
方方不能在当天11点30分前到达B地 理由:8点至11点30分的时长为
h,将t=代入v=,得v=137.∵
137>120,即小汽车超速了,∴
方方不能在当天11点30分前到达B地.
(1)
设线段AB所在直线对应的函数解析式为y=k1x+b(k1≠0),把(0,10),(2,14)代入,得解得∴
线段AB所在直线对应的函数解析式为y=2x+10.∵
点B在线段AB上,∴
当x=5时,y=20.∴
点B的坐标为(5,20).∴
线段BC所在直线对应的函数解析式为y=20.设双曲线CD对应的函数解析式为y=(k2≠0),∵
C(10,20)在双曲线上,∴
k2=200.∴
双曲线CD对应的函数解析式为y=.∴
y与x的函数解析式为y= (2)
由(1)可知,恒温系统设定的恒定温度为20
℃ (3)
把y=10代入y=中,解得x=20,∴
20-10=10(h).答:恒温系统最多关闭10
h,蔬菜才能避免受到伤害
(1)
观察图象,可知当x=7时,y=100.当0≤x≤7时,设y关于x的函数解析式为y=kx+b,将点(0,30),(7,100)代入,得解得∴
当0≤x≤7时,y关于x的函数解析式为y=10x+30;当x>7时,设y=,将点(7,100)代入,得100=,解得a=700.∴
当x>7时,y关于x的函数解析式为y=.当y=30时,x=.∴
y与x之间的函数解析式为y= (2)
将y=50代入y=10x+30,得x=2;将y=50代入y=,得x=14.+2-14=(min).答:怡萱同学想喝高于50
℃的水,她最多需要等待
min
17
一、
选择题
1.
(2019·孝感)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1
200
N和0.5
m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A.
F=
B.
F=
C.
F=
D.
F=
2.
(2019·上海)下列函数中,函数值y随自变量x的值增大而增大的是( )
A.
y=
B.
y=-
C.
y=
D.
y=-
3.
(2019·柳州)反比例函数y=的图象位于( )
A.
第一、三象限
B.
第二、三象限
C.
第一、二象限
D.
第二、四象限
4.
(2019·淮安)当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是( )
5.
(2019·江西)已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下列说法正确的是
( )
A.
反比例函数y2的解析式是y2=-
B.
两个函数图象的另一交点坐标为(2,-4)
C.
当x<-2或0<x<2时,y1<y2
D.
正比例函数y1与反比例函数y2都随x的增大而增大
6.
(2019·安徽)已知点A(1,-3)关于x轴的对称点A′在反比例函数y=的图象上,则实数k的值为( )
A.
3
B.
C.
-3
D.
-
7.
(2019·哈尔滨)点(-1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是( )
A.
(4,-1)
B.
C.
(-4,-1)
D.
8.
(2019·毕节)若点A(-4,y1),B(-2,y2),C(2,y3)都在反比例函数y=-的图象上,则y1,y2,y3的大小关系是( )
A.
y1>y2>y3
B.
y3>y2>y1
C.
y2>y1>y3
D.
y1>y3>y2
9.
(2019·崇左)若点(-1,y1),(2,y2),(3,y3)在反比例函数y=(k<0)的图象上,则y1,y2,y3的大小关系是( )
A.
y1>y2>y3
B.
y3>y2>y1
C.
y1>y3>y2
D.
y2>y3>y1
10.
(2019·徐州)若A(x1,y1),B(x2,y2)都在函数y=的图象上,且x1<0<x2,则( )
A.
y1<y2
B.
y1=y2
C.
y1>y2
D.
y1=-y2
11.
(2019·河北)如图,函数y=的图象所在坐标系的原点是( )
A.
点M
B.
点N
C.
点P
D.
点Q
12.
(2019·西藏)已知A是直线y=2x与双曲线y=(m为常数)一支的交点,过点A作x轴的垂线,垂足为B,且OB=2,则m的值为( )
A.
-7
B.
-8
C.
8
D.
7
13.
(2019·日照)在同一平面直角坐标系中,函数y=kx+1(k≠0)和y=(k≠0)的图象大致是( )
14.
(2019·济南)如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k的值为( )
A.
1
B.
2
C.
3
D.
4
15.
(2019·泸州)如图,一次函数y1=ax+b和反比例函数y2=的图象相交于A,B两点,则使y1>y2成立的x的取值范围是( )
A.
-2<x<0或0<x<4
B.
x<-2或0<x<4
C.
x<-2或x>4
D.
-2<x<0或x>4
16.
(2019·鸡西)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数y=的图象上,顶点B在反比例函数y=的图象上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A.
B.
C.
4
D.
6
17.
(2019·娄底)如图,⊙O的半径为2,双曲线对应的函数解析式分别为y=和y=-,则阴影部分的面积是( )
A.
4π
B.
3π
C.
2π
D.
π
18.
(2019·长春)如图,在平面直角坐标系中,Rt△ABC的顶点A,C的坐标分别是(0,3),(3,0),∠ACB=90°,AC=2BC.若函数y=(k>0,x>0)的图象经过点B,则k的值为( )
A.
B.
9
C.
D.
二、
填空题
19.
(2019·云南)若点(3,5)在反比例函数y=(k≠0)的图象上,则k=________.
20.
(2019·镇江)若已知点A(-2,y1),B(-1,y2)都在反比例函数y=-的图象上,则y1________y2(填“>”或“<”
).
21.
(2019·山西)如图,在平面直角坐标系中,点O为坐标原点,菱形ABCD的顶点B在x轴的正半轴上,点A的坐标为(-4,0),点D的坐标为(-1,4),反比例函数y=(x>0)的图象恰好经过点C,则k的值为________.
22.
(2019·绥化)一次函数y1=-x+6与反比例函数y2=(x>0)的图象如图所示,当y1>y2时,自变量x的取值范围是________.
23.
(2019·青海)如图,P是反比例函数y=图象上的一点,过点P向x轴作垂线,垂足为A,连接OP.若图中涂色部分的面积是1,则此反比例函数的解析式为________.
24.
(2019·安顺)如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于A,B两点,连接OA,OB,已知△OAB的面积为4,则k1-k2=________.
25.
(2019·北京)在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=上,点A关于x轴的对称点B在双曲线y=上,则k1+k2的值为________.
26.
(2019·黄冈)如图,一直线经过原点O,且与反比例函数y=(k>0)的图象相交于点A,B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC的面积为8,则k=________.
27.
(2019·陕西)如图,D是矩形AOBC的对称中心,A(0,4),B(6,0),若一个反比例函数的图象经过点D,交AC于点M,则点M的坐标为________.
28.
(2019·荆门)如图,在平面直角坐标系中,函数y=(k>0,x>0)的图象与等边三角形OAB的边OA,AB分别交于点M,N,且OM=2MA,若AB=3,那么点N的横坐标为________.
29.
(2019·新疆)如图,在平面直角坐标系中,已知正比例函数y=-2x与反比例函数y=的图象交于A(a,-4),B两点,过原点O的另一条直线l与双曲线y=交于P,Q两点(点P在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是____.
30.
(2019·深圳)如图,在Rt△ABC中,∠ABC=90°,C(0,-3),CD=3AD,点A在反比例函数y=的图象上,且y轴平分∠ACB,则k=________.
31.(2019·孝感)如图,双曲线y=(x>0)经过矩形OABC的顶点B,双曲线y=(x>0)交AB,BC于点E,F,且与矩形的对角线OB交于点D,连接EF.
若OD∶OB=2∶3,则△BEF的面积为________.
32.
(2019·南通)如图,过点C(3,4)的直线y=2x+b交x轴于点A,∠ABC=90°,AB=CB,曲线y=(x>0)过点B,将点A沿y轴正方向平移a个单位长度恰好落在该曲线上,则a的值为________.
三、
解答题
33.
(2019·常州)如图,在?OABC中,OA=2,∠AOC=45°,点C在y轴上,D是BC的中点,反比例函数y=(x>0)的图象经过点A,D.求:
(1)
k的值;
(2)
点D的坐标.
第33题
34.(2019·盐城)如图,一次函数y=x+1的图象交y轴于点A,与反比例函数y=(x>0)的图象交于点B(m,2).求:
(1)
反比例函数的解析式;
(2)
△AOB的面积.
第34题
35.(2019·宿迁)如图,一次函数y=kx+b的图象与反比例函数y=-的图象相交于A(-1,m),B(n,-1)两点.求:
(1)
一次函数的解析式;
(2)
△AOB的面积.
第35题
36.(2019·东营)如图,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a),B两点,BC⊥x轴,垂足为C,△AOC的面积是2.求:
(1)
m,n的值;
(2)
直线AC对应的函数解析式.
第36题
37.(2019·广东)如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A,B两点,其中点A的坐标为(-1,4),点B的坐标为(4,n).
(1)
根据图象,直接写出满足k1x+b>的x的取值范围;
(2)
求这两个函数的解析式;
(3)
点P在线段AB上,且S△AOP∶S△BOP=1∶2,求点P的坐标.
第37题
38.
(2019·葫芦岛)如图,一次函数y=k1x+b的图象与x轴,y轴分别交于A,B两点,与反比例函数y=的图象分别交于C,D两点,点C的坐标为(2,4),B是线段AC的中点.
(1)
求一次函数y=k1x+b与反比例函数y=的解析式;
(2)
求△COD的面积;
(3)
直接写出当x取什么值时,k1x+b<.
第38题
39.(2019·大庆)如图,反比例函数y=和一次函数y=kx-1的图象相交于A(m,2m),B两点.
(1)
求一次函数的解析式;
(2)
求出点B的坐标,并根据图象直接写出满足不等式<kx-1的x的取值范围.
第39题
40.(2019·湘西州)如图,一次函数y=kx+b的图象与反比例函数y=的图象在第一象限交于点A(3,2),与y轴的负半轴交于点B,且OB=4.
(1)
求函数y=和y=kx+b的解析式;
(2)
结合图象直接写出不等式组0<<kx+b的解集.
第40题
41.
(2019·襄阳)如图,一次函数y1=kx+b与反比例函数y2=的图象在第一、三象限分别交于A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)
求一次函数和反比例函数的解析式;
(2)
比较大小:AD________BC(填“>”“<”或“=”);
(3)
直接写出y1<y2时,x的取值范围.
第41题
42.
(2019·大连)如图,在平面直角坐标系xOy中,点A(3,2)在反比例函数y=(x>0)的图象上,点B在OA的延长线上,BC⊥x轴,垂足为C,BC与反比例函数的图象相交于点D,连接AC,AD.
(1)
求该反比例函数的解析式;
(2)
若S△ACD=,设点C的坐标为(a,0),求线段BD的长.
第42题
43.(2019·雅安)如图,在平面直角坐标系中,一次函数y=-x+m的图象与反比例函数y=(x>0)的图象交于A,B两点,已知A(2,4).
(1)
求一次函数和反比例函数的解析式;
(2)
求点B的坐标;
(3)
连接AO,BO,求△AOB的面积.
第43题
44.
((2019·成都)如图,在平面直角坐标系xOy中,一次函数y=x+5和y=-2x的图象相交于点A,反比例函数y=的图象经过点A.
(1)
求反比例函数的解析式;
(2)
设一次函数y=x+5的图象与反比例函数y=的图象的另一个交点为B,连接OB,求△ABO的面积.
第44题
45.(2018·河南)小明在研究矩形面积S与矩形的边长x,y之间的关系时,得到如下数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
4
3
2
■
1
0.5
结果发现一个数据被墨水涂黑了.
(1)
被墨水涂黑的数据为________.
(2)
y与x之间的函数解析式为________,且y随x的增大而________.
(3)
如图是小明画出的y关于x的函数图象,点B,E均在该函数的图象上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1和S2的大小关系,并说明理由.
(4)
在(3)的条件下,DE交BC于点G,反比例函数y=的图象经过点G,交AB于点H,连接OG,OH,则四边形OGBH的面积为________.
第45题
46.(2019·杭州)方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480
km,设小汽车的行驶时间为t(h),行驶速度为v(km/h),且全程速度限定为不超过120
km/h.
(1)
求v关于t的函数解析式;
(2)
方方上午8点驾驶小汽车从A地出发.
①
方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②
方方能否在当天11点30分前到达B地?说明理由.
47.(2018·乐山)某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y
(℃)与时间x(h)之间的函数关系,其中线段AB,BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)
求y与x(0≤x≤24)的函数解析式;
(2)
求恒温系统设定的恒定温度;
(3)
若大棚内的温度低于10
℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多长时间,才能使蔬菜避免受到伤害?
第47题
48.
(2019·鄂尔多斯)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10
℃,加热到100
℃停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30
℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30
℃时接通电源,水温y(℃)与时间x(min)的关系如图所示.
(1)
分别写出水温上升和下降阶段y与x之间的函数解析式;
(2)
怡萱同学想喝高于50
℃的水,请问她最多需要等待多长时间?
第48题
参考答案
一、
B
A
A
B
C
A
A
C
C
A
A
D
C
D
B
C
C
D
二、
15
<
16
2
8
0
8
(-4,2)或(-1,8)
4
三、
(1)
过点A作AH⊥y轴于点H.在Rt△AOH中,∵
∠AOC=45°,OA=2,∴
OH=AH=2.∴
点A的坐标为(2,2).∴
k=4 (2)
∵
四边形OABC是平行四边形,∴
OC∥AB.∴
AB⊥x轴.∴
点B的横坐标为2.∵
D是BC的中点,∴
点D的横坐标为1.又由(1),知反比例函数的解析式为y=,且点D在其图象上,∴
点D的坐标为(1,4)
(1)
∵
点B(m,2)在一次函数y=x+1的图象上,∴
2=m+1,解得m=1.∴
点B的坐标为(1,2).∵
点B(1,2)在反比例函数y=(x>0)的图象上,∴
k=2×1=2,即反比例函数的解析式是y= (2)
将x=0代入y=x+1,得y=1,则点A的坐标为(0,1).∵
点B的坐标为(1,2),∴
S△AOB=×1×1=
(1)
把A(-1,m),B(n,-1)分别代入y=-,得m=5,n=5,∴
点A的坐标为(-1,5),点B的坐标为(5,-1).把A(-1,5),B(5,-1)代入y=kx+b,得解得∴
一次函数的解析式为y=-x+4 (2)
如图,当x=0时,y=4,∴
OD=4.∴
S△AOB=S△AOD+S△BOD=×4×1+×4×5=12
(1)
∵
直线y=mx与双曲线y=相交于A(-2,a),B两点,∴
点A与点B关于原点成中心对称.∴
点B的坐标为(2,-a).∴
点C的坐标为(2,0).∴
OC=2.∵
S△AOC=2,∴
×2a=2,解得a=2.∴
点A的坐标为(-2,2).把A(-2,2)代入y=mx和y=,得解得 (2)
设直线AC对应的函数解析式为y=kx+b,∵
直线经过点A,C,∴
解得∴
直线AC对应的函数解析式为y=-x+1
(1)
x<-1或0<x<4 (2)
∵
反比例函数y=的图象过点A(-1,4),B(4,n),∴
k2=-1×4=-4,k2=4n.∴
n=-1.∴
点B的坐标为(4,-1).∵
一次函数y=k1x+b的图象过点A,B,∴
解得∴
一次函数的解析式为y=-x+3,反比例函数的解析式为y=- (3)
设直线AB与y轴的交点为C,则点C的坐标为(0,3).∴
S△AOB=S△AOC+S△BOC=×3×1+×3×4=.∵
S△AOP∶S△BOP=1∶2,∴
S△AOP=×=.∴
S△COP=S△AOP-S△AOC=-=1.∴
×3·xP=1.∴
xP=.∵
点P在线段AB上,∴
y=.∴
点P的坐标为
(1)
∵
点C(2,4)在反比例函数y=的图象上,∴
k2=2×4=8.∴
反比例函数的解析式为y=.如图,过点C作CE⊥x轴于点E,∵
C(2,4),B是线段AC的中点,∴
易得点B的坐标为(0,2).∵
B,C两点在一次函数y=k1x+b的图象上,∴
解得∴
一次函数的解析式为y=x+2
(2)
由解得或∴
点D的坐标为(-4,-2).∴
S△COD=S△BOC+S△BOD=×2×2+×2×4=6 (3)
由图象,可得当0<x<2或x<-4时,k1x+b<
(1)
∵
A(m,2m)在反比例函数y=的图象上,∴
2m=.∴
m=1.∴
点A的坐标为(1,2).又∵
点A(1,2)在一次函数y=kx-1的图象上,∴
2=k-1,即k=3.∴
一次函数的解析式为y=3x-1 (2)
联立解得或∴
点B的坐标为.由图象,知满足不等式<kx-1的x的取值范围为-<x<0或x>1
(1)
把点A(3,2)代入反比例函数y=,可得m=3×2=6,∴
反比例函数的解析式为y=.∵
OB=4,∴
点B的坐标为(0,-4).把点A(3,2),B(0,-4)代入一次函数y=kx+b,可得解得∴
一次函数的解析式为y=2x-4
(2)
x>3
(1)
把A(3,4)代入反比例函数y2=,得4=,解得m=12.∴
反比例函数的解析式为y2=.∵
点B(a,-2)在反比例函数y2=的图象上,∴
-2a=12,解得a=-6.∴
点B的坐标为(-6,-2).∵
一次函数y1=kx+b的图象经过A(3,4),B(-6,-2)两点,∴
解得∴
一次函数的解析式为y1=x+2 (2)
= (3)
由图象,可知当y1<y2时,x的取值范围是x<-6或0<x<3
(1)
∵
点A(3,2)在反比例函数y=(x>0)的图象上,∴
k=3×2=6.∴
反比例函数的解析式为y= (2)
如图,过点A作AE⊥OC,垂足为E,设直线OA对应的函数解析式为y=mx,将A(3,2)代入,得2=3m,解得m=.∴
直线OA对应的函数解析式为y=x.∵
点C的坐标为(a,0),BC⊥x轴,把x=a代入y=x,得y=a,∴
点B的坐标为.∴
BC=a.把x=a代入y=,得y=.∴
点D的坐标为.∴
CD=.∵
S△ACD=,∴
CD·EC=,即··(a-3)=,解得a=6.∴
BD=BC-CD=a-=3
(1)
将A(2,4)代入y=-x+m与y=(x>0)中,得4=-2+m,4=,∴
m=6,k=8.∴
一次函数的解析式为y=-x+6,反比例函数的解析式为y= (2)
联立解得或∴
点B的坐标为(4,2) (3)
设直线y=-x+6与y轴交于点C,易得点C的坐标为(0,6),∴
OC=6.∴
易得S△AOB=S△COB-S△AOC=×6×4-×6×2=6
(1)
由解得∴
点A的坐标为(-2,4).∵
反比例函数y=的图象经过点A,∴
k=-2×4=-8.∴
反比例函数的解析式是y=- (2)
联立解得或∴
点B的坐标为(-8,1).∵
直线AB对应的函数解析式为y=x+5,∴
易得直线AB与x轴的交点坐标为(-10,0).∴
S△ABO=×10×4-×10×1=15
(1)
1.5 (2)
y= 减小 (3)
S1=S2 理由:∵
S1=OA·AB=6,S2=OD·DE=6,∴
S1=S2. (4)
4
(1)
∵
vt=480,且全程速度限定为不超过120
km/h,∴
v关于t的函数解析式为v=(t≥4) (2)
①
8点至12点48分的时长为
h,8点至14点的时长为6
h,将t=6代入v=,得v=80;将t=代入v=,得v=100.∴
小汽车行驶速度v的范围为80≤v≤100 ②
方方不能在当天11点30分前到达B地 理由:8点至11点30分的时长为
h,将t=代入v=,得v=137.∵
137>120,即小汽车超速了,∴
方方不能在当天11点30分前到达B地.
(1)
设线段AB所在直线对应的函数解析式为y=k1x+b(k1≠0),把(0,10),(2,14)代入,得解得∴
线段AB所在直线对应的函数解析式为y=2x+10.∵
点B在线段AB上,∴
当x=5时,y=20.∴
点B的坐标为(5,20).∴
线段BC所在直线对应的函数解析式为y=20.设双曲线CD对应的函数解析式为y=(k2≠0),∵
C(10,20)在双曲线上,∴
k2=200.∴
双曲线CD对应的函数解析式为y=.∴
y与x的函数解析式为y= (2)
由(1)可知,恒温系统设定的恒定温度为20
℃ (3)
把y=10代入y=中,解得x=20,∴
20-10=10(h).答:恒温系统最多关闭10
h,蔬菜才能避免受到伤害
(1)
观察图象,可知当x=7时,y=100.当0≤x≤7时,设y关于x的函数解析式为y=kx+b,将点(0,30),(7,100)代入,得解得∴
当0≤x≤7时,y关于x的函数解析式为y=10x+30;当x>7时,设y=,将点(7,100)代入,得100=,解得a=700.∴
当x>7时,y关于x的函数解析式为y=.当y=30时,x=.∴
y与x之间的函数解析式为y= (2)
将y=50代入y=10x+30,得x=2;将y=50代入y=,得x=14.+2-14=(min).答:怡萱同学想喝高于50
℃的水,她最多需要等待
min
