沪科版八年级数学下册第18章 直角三角形与勾股定理中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版八年级数学下册第18章 直角三角形与勾股定理中考题汇编(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 67.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 18:26:19 | ||
图片预览


文档简介
沪科版八年级数学下册直角三角形与勾股定理中考题汇编(含答案)
一、
选择题
1.
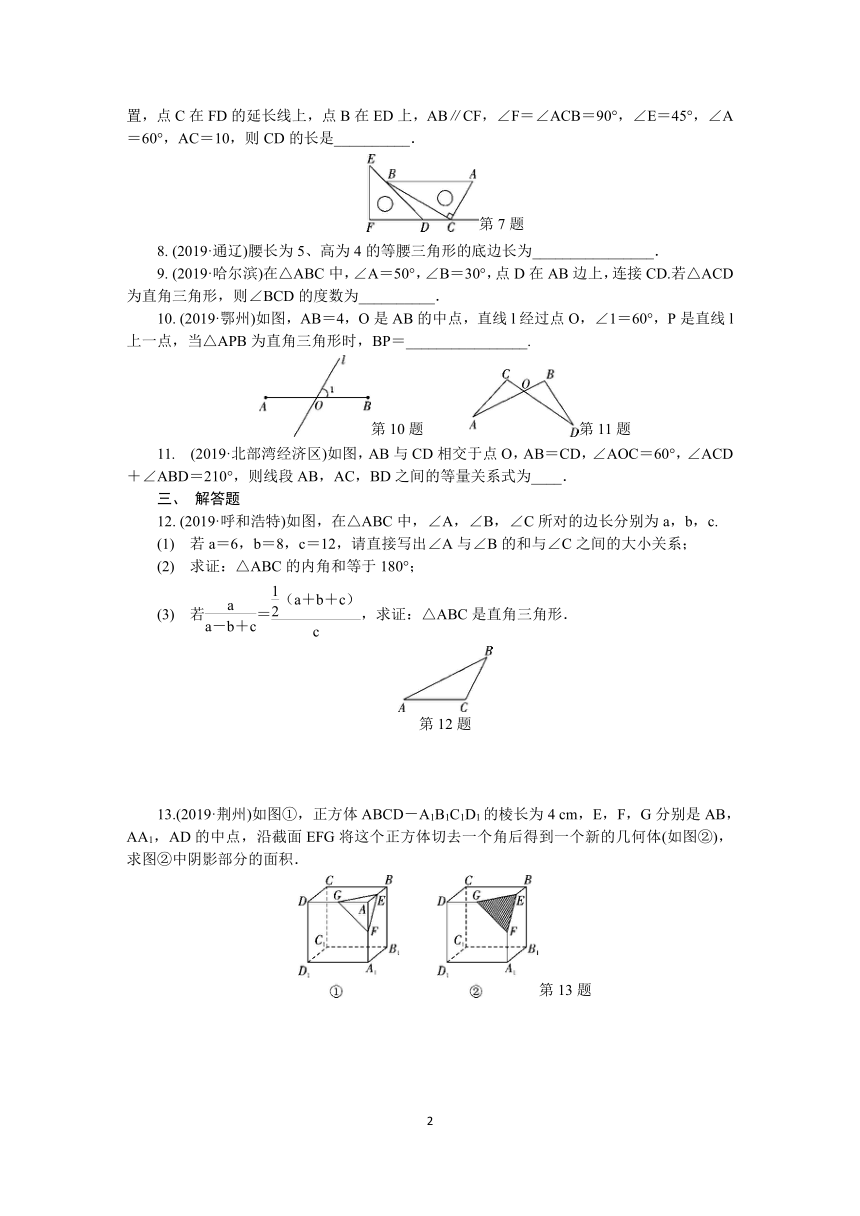
(2019·毕节)如图,点E在正方形ABCD的边AB上.若EB=1,EC=2,则正方形ABCD的面积为( )
A.
B.
3
C.
D.
5
2.
(2019·湖州)在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线把平行四边形分成面积相等的两部分.如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A.
2
B.
C.
D.
3.
(2019·宁波)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按如图②所示的方式放置在最大正方形内.若知道图②中涂色部分的面积,则一定能求出( )
A.
直角三角形的面积
B.
最大正方形的面积
C.
较小两个正方形重叠部分的面积
D.
最大正方形与直角三角形的面积和
二、
填空题
4.
(2019·常州)在平面直角坐标系中,点P(-3,4)到原点的距离是________.
5.
(2019·东营)已知等腰三角形的底角是30°,腰长为2,则它的周长是__________.
6.
(2019·枣庄)把两块同样大小含45°的三角尺按如图所示的方式放置,其中一块三角尺的锐角顶点与另一块三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD=________.
7.
(2019·毕节)三角尺是我们学习数学的好帮手.将一对直角三角尺按如图所示的方式放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长是__________.
8.
(2019·通辽)腰长为5、高为4的等腰三角形的底边长为________________.
9.
(2019·哈尔滨)在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD.若△ACD为直角三角形,则∠BCD的度数为__________.
10.
(2019·鄂州)如图,AB=4,O是AB的中点,直线l经过点O,∠1=60°,P是直线l上一点,当△APB为直角三角形时,BP=________________.
11.
(2019·北部湾经济区)如图,AB与CD相交于点O,AB=CD,∠AOC=60°,∠ACD+∠ABD=210°,则线段AB,AC,BD之间的等量关系式为____.
三、
解答题
12.
(2019·呼和浩特)如图,在△ABC中,∠A,∠B,∠C所对的边长分别为a,b,c.
(1)
若a=6,b=8,c=12,请直接写出∠A与∠B的和与∠C之间的大小关系;
(2)
求证:△ABC的内角和等于180°;
(3)
若=,求证:△ABC是直角三角形.
第12题
13.(2019·荆州)如图①,正方体ABCD-A1B1C1D1的棱长为4
cm,E,F,G分别是AB,AA1,AD的中点,沿截面EFG将这个正方体切去一个角后得到一个新的几何体(如图②),求图②中阴影部分的面积.
14.(2019·巴中)如图,等腰直角三角尺如图放置.直角顶点C在直线m上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m于点D.
(1)
求证:EC=DB;
(2)
若△AEC的三边长分别为a,b,c,利用此图证明勾股定理.
第14题
15.(2019·河北)已知:整式A=(n2-1)2+(2n)2,整式B>0.
【尝试】
(1)
化简整式A.
【发现】
(2)
A=B2,求整式B.
【联想】
(3)
由上可知,B2=(n2-1)2+(2n)2,当n>1时,n2-1,2n,B为直角三角形的三边长(如图).填写下表中B的值:
直角三角形三边
n2-1
2n
B
勾股数组Ⅰ
/
8
勾股数组Ⅱ
35
/
16.
(2019·枣庄)在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)
如图①,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;
(2)
如图②,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(3)
如图③,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=AM.
3
参考答案
一、
B
D
C
二、
5
6+4
-
15-5
6或2或4
60°或10°
2或2或2
AB2=AC2+BD2
三、
(1)
∠C>∠A+∠B (2)
如图,过点B作直线DE∥AC,∴
∠A=∠ABD,∠C=∠CBE.又∵
∠ABD+∠ABC+∠CBE=180°,∴
∠A+∠ABC+∠C=180°.∴
△ABC的内角和等于180° (3)
原式可变形为=.∴
(a+c)2-b2=2ac,即a2+2ac+c2-b2=2ac.∴
a2+c2=b2.∴
△ABC是直角三角形,且∠B=90°
∵
正方体ABCD-A1B1C1D1的棱长为4
cm,E,F,G分别是AB,AA1,AD的中点,∴
易得GF=GE=EF==2(cm).∴
△GFE是等边三角形.如图,过点G作GH⊥EF于点H.∴
FH=HE=
cm.∴
在Rt△GHF中,GH===(cm).∴
题图②中阴影部分的面积为×2×=2(cm2)
(1)
由题意,得AC=CB,∠ACB=90°,∴
∠ACE+∠BCD=90°.∵
AE⊥直线m于点E,BD⊥直线m于点D,∴
∠AEC=∠BDC=90°.∴
∠ACE+∠CAE=90°.∴
∠CAE=∠BCD.在△CAE和△BCD中,∴
△CAE≌△BCD.∴
EC=DB (2)
∵
△CAE≌△BCD,∴
BD=CE=a,CD=AE=b.∴
S梯形AEDB=(a+b)(a+b)=a2+ab+b2.又∵
S梯形AEDB=S△AEC+S△BCD+S△ABC=ab+ab+c2=ab+c2.∴
a2+ab+b2=ab+c2.整理,得a2+b2=c2
(1)
A=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1 (2)
∵
A=n4+2n2+1=(n2+1)2,又∵
A=B2,B>0,∴
B=n2+1 (3)
17 37
(1)
∵
∠BAC=90°,AB=AC,AD⊥BC,∴
AD=BD=DC,∠ABC=∠ACB=45°,∠BAD=∠CAD=45°.∵
AB=2,∴
在Rt△ABD中,由勾股定理,得BD=.∴
AD=DC=BD=.∵
∠AMN=30°,∴
∠BMD=180°-90°-30°=60°.∴
∠MBD=30°.∴
BM=2DM.在Rt△BMD中,由勾股定理,得BM2-DM2=BD2,即(2DM)2-DM2=()2,解得DM=(负值舍去).∴
AM=AD-DM=- (2)
∵
AD⊥BC,∴
∠ADB=∠EDF=90°.∴
∠ADB-∠ADE=∠EDF-∠ADE,即∠BDE=∠ADF.又由(1),得AD=BD,∠B=∠DAF=45°,∴
在△BDE和△ADF中,∴
△BDE≌△ADF.∴
BE=AF (3)
过点M作ME∥BC交AB的延长线于点E.∵
ME∥BC,∠ABC=45°,AD⊥BC,∴
∠AME=∠ADB=90°,∠BEM=∠ABD=45°.∴
AM=ME.∴
在Rt△AME中,由勾股定理,得AE==AM.∵
∠AME=∠BMN=90°,∴
∠BME=∠NMA.在△BME和△NMA中,∴
△BME≌△NMA.∴
BE=NA.∴
AB+AN=AB+BE=AE=AM
一、
选择题
1.
(2019·毕节)如图,点E在正方形ABCD的边AB上.若EB=1,EC=2,则正方形ABCD的面积为( )
A.
B.
3
C.
D.
5
2.
(2019·湖州)在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线把平行四边形分成面积相等的两部分.如图是由5个边长为1的小正方形拼成的图形,P是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A.
2
B.
C.
D.
3.
(2019·宁波)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按如图②所示的方式放置在最大正方形内.若知道图②中涂色部分的面积,则一定能求出( )
A.
直角三角形的面积
B.
最大正方形的面积
C.
较小两个正方形重叠部分的面积
D.
最大正方形与直角三角形的面积和
二、
填空题
4.
(2019·常州)在平面直角坐标系中,点P(-3,4)到原点的距离是________.
5.
(2019·东营)已知等腰三角形的底角是30°,腰长为2,则它的周长是__________.
6.
(2019·枣庄)把两块同样大小含45°的三角尺按如图所示的方式放置,其中一块三角尺的锐角顶点与另一块三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD=________.
7.
(2019·毕节)三角尺是我们学习数学的好帮手.将一对直角三角尺按如图所示的方式放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长是__________.
8.
(2019·通辽)腰长为5、高为4的等腰三角形的底边长为________________.
9.
(2019·哈尔滨)在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD.若△ACD为直角三角形,则∠BCD的度数为__________.
10.
(2019·鄂州)如图,AB=4,O是AB的中点,直线l经过点O,∠1=60°,P是直线l上一点,当△APB为直角三角形时,BP=________________.
11.
(2019·北部湾经济区)如图,AB与CD相交于点O,AB=CD,∠AOC=60°,∠ACD+∠ABD=210°,则线段AB,AC,BD之间的等量关系式为____.
三、
解答题
12.
(2019·呼和浩特)如图,在△ABC中,∠A,∠B,∠C所对的边长分别为a,b,c.
(1)
若a=6,b=8,c=12,请直接写出∠A与∠B的和与∠C之间的大小关系;
(2)
求证:△ABC的内角和等于180°;
(3)
若=,求证:△ABC是直角三角形.
第12题
13.(2019·荆州)如图①,正方体ABCD-A1B1C1D1的棱长为4
cm,E,F,G分别是AB,AA1,AD的中点,沿截面EFG将这个正方体切去一个角后得到一个新的几何体(如图②),求图②中阴影部分的面积.
14.(2019·巴中)如图,等腰直角三角尺如图放置.直角顶点C在直线m上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m于点D.
(1)
求证:EC=DB;
(2)
若△AEC的三边长分别为a,b,c,利用此图证明勾股定理.
第14题
15.(2019·河北)已知:整式A=(n2-1)2+(2n)2,整式B>0.
【尝试】
(1)
化简整式A.
【发现】
(2)
A=B2,求整式B.
【联想】
(3)
由上可知,B2=(n2-1)2+(2n)2,当n>1时,n2-1,2n,B为直角三角形的三边长(如图).填写下表中B的值:
直角三角形三边
n2-1
2n
B
勾股数组Ⅰ
/
8
勾股数组Ⅱ
35
/
16.
(2019·枣庄)在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)
如图①,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;
(2)
如图②,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(3)
如图③,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=AM.
3
参考答案
一、
B
D
C
二、
5
6+4
-
15-5
6或2或4
60°或10°
2或2或2
AB2=AC2+BD2
三、
(1)
∠C>∠A+∠B (2)
如图,过点B作直线DE∥AC,∴
∠A=∠ABD,∠C=∠CBE.又∵
∠ABD+∠ABC+∠CBE=180°,∴
∠A+∠ABC+∠C=180°.∴
△ABC的内角和等于180° (3)
原式可变形为=.∴
(a+c)2-b2=2ac,即a2+2ac+c2-b2=2ac.∴
a2+c2=b2.∴
△ABC是直角三角形,且∠B=90°
∵
正方体ABCD-A1B1C1D1的棱长为4
cm,E,F,G分别是AB,AA1,AD的中点,∴
易得GF=GE=EF==2(cm).∴
△GFE是等边三角形.如图,过点G作GH⊥EF于点H.∴
FH=HE=
cm.∴
在Rt△GHF中,GH===(cm).∴
题图②中阴影部分的面积为×2×=2(cm2)
(1)
由题意,得AC=CB,∠ACB=90°,∴
∠ACE+∠BCD=90°.∵
AE⊥直线m于点E,BD⊥直线m于点D,∴
∠AEC=∠BDC=90°.∴
∠ACE+∠CAE=90°.∴
∠CAE=∠BCD.在△CAE和△BCD中,∴
△CAE≌△BCD.∴
EC=DB (2)
∵
△CAE≌△BCD,∴
BD=CE=a,CD=AE=b.∴
S梯形AEDB=(a+b)(a+b)=a2+ab+b2.又∵
S梯形AEDB=S△AEC+S△BCD+S△ABC=ab+ab+c2=ab+c2.∴
a2+ab+b2=ab+c2.整理,得a2+b2=c2
(1)
A=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1 (2)
∵
A=n4+2n2+1=(n2+1)2,又∵
A=B2,B>0,∴
B=n2+1 (3)
17 37
(1)
∵
∠BAC=90°,AB=AC,AD⊥BC,∴
AD=BD=DC,∠ABC=∠ACB=45°,∠BAD=∠CAD=45°.∵
AB=2,∴
在Rt△ABD中,由勾股定理,得BD=.∴
AD=DC=BD=.∵
∠AMN=30°,∴
∠BMD=180°-90°-30°=60°.∴
∠MBD=30°.∴
BM=2DM.在Rt△BMD中,由勾股定理,得BM2-DM2=BD2,即(2DM)2-DM2=()2,解得DM=(负值舍去).∴
AM=AD-DM=- (2)
∵
AD⊥BC,∴
∠ADB=∠EDF=90°.∴
∠ADB-∠ADE=∠EDF-∠ADE,即∠BDE=∠ADF.又由(1),得AD=BD,∠B=∠DAF=45°,∴
在△BDE和△ADF中,∴
△BDE≌△ADF.∴
BE=AF (3)
过点M作ME∥BC交AB的延长线于点E.∵
ME∥BC,∠ABC=45°,AD⊥BC,∴
∠AME=∠ADB=90°,∠BEM=∠ABD=45°.∴
AM=ME.∴
在Rt△AME中,由勾股定理,得AE==AM.∵
∠AME=∠BMN=90°,∴
∠BME=∠NMA.在△BME和△NMA中,∴
△BME≌△NMA.∴
BE=NA.∴
AB+AN=AB+BE=AE=AM
