华东师大版九年级数学上册 第21章 二次根式 单元测试题(Word版有答案)
文档属性
| 名称 | 华东师大版九年级数学上册 第21章 二次根式 单元测试题(Word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 33.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览



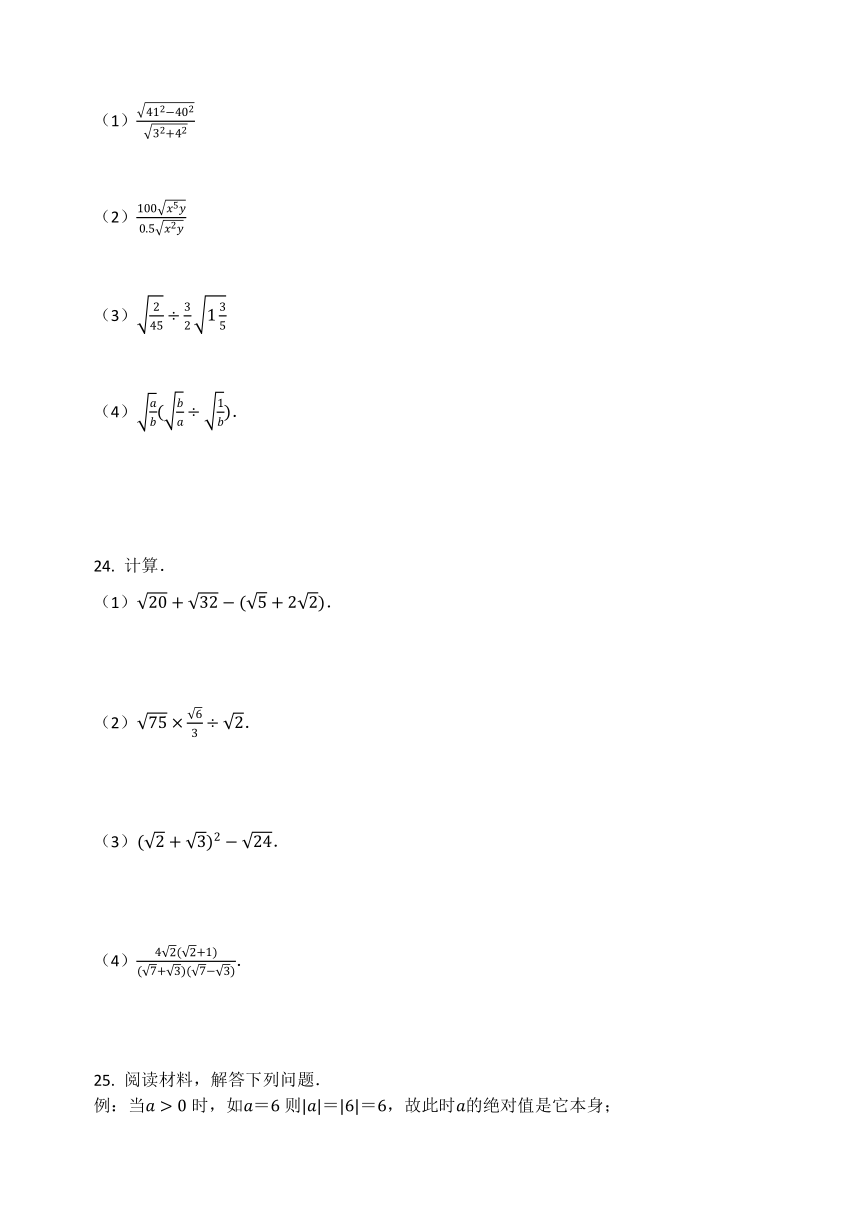

文档简介
第21章
二次根式
单元测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
1.
化简的结果是?
?
?
?
A.
B.
C.
D.
?
2.
给出下列各数:①②③④,其中是方程的解的个数有(
)
A.个
B.个
C.个
D.个
?
3.
下列二次根式中,最简二次根式是(?
?
?
?
)
A.
B.
C.
D.
?
4.
化简的结果为(
)
A.
B.
C.
D.
?
5.
已知,,则代数式的值为(
)
A.
B.
C.
D.
?
6.
化简二次根式的正确结果是???
A.
B.
C.
D.
?
7.
化简+-的结果为??????
A.
B.
C.
D.
?8.
下列计算正确的是(
)
A.
B.=
C.=
D.=
?
9.
已知为实数,则代数式的最小值为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
10.
在中,是最简二次根式的是________.
?
11.
计算的结果等于________.
?
12.
若等式成立,则的取值范围是________.
?
13.
在实数范围内,使二次根式有意义的的取值范围是________.
?
14.
若矩形的长为,宽为,则此矩形的面积为________?.
?
15.
二次根式中的取值范围是________.
?
16.
若二次根式有意义,则的取值范围为________.
?
17.
计算________.
?
18.
化简并计算:________.(结果中分母不含根式)
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
设长方形的面积为,相邻两边分别为,
(1)已知,,求;
(2)已知=,=,求.
?
20.
已知,求的值.
?
21.
若最简二次根式与是同类二次根式,求的值.
?
22.
计算:
.
?23.
计算:
(1)
(2)
(3)
(4).
?
24.
计算.
(1).
(2).
(3).
(4).
?
25.
阅读材料,解答下列问题.
例:当时,如=则==,故此时的绝对值是它本身;
当=时,=,故此时的绝对值是零;
当时,如=则==,故此时的绝对值是它的相反数.
∴
综合起来一个数的绝对值要分三种情况,即,
这种分析方法渗透了数学的分类讨论思想.
问:(
(1))请仿照例中的分类讨论的方法,分析二次根式的各种展开的情况;
(2)猜想与的大小关系.
参考答案与试题解析
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
)
1.
【答案】
B
【解答】
解:.
故选.
2.
【答案】
A
【解答】
=,
解得;=,,
故①②③④,其中是方程的解.
3.
【答案】
A
【解答】
解:、是最简二次根式;?
、,被开方数含能开得尽方的因数,不是最简二次根式;
、,被开方数含分母,不是最简二次根式;
、,被开方数含分母,不是最简二次根式.
故选.
4.
【答案】
D
【解答】
解:∵
有意义,
∴
,
∴
,
∴
,
∴
.
故选.
5.
【答案】
B
【解答】
解:当,时,
.
故选:.
6.
【答案】
【解答】
解:…二次根式有意义,则,即
…原式
故选:.
7.
【答案】
【解答】
此题暂无解答
8.
【答案】
A
【解答】
、,故此选项正确;
、=,故此选项错误;
、=,故此选项错误;
、无法计算,故此选项错误;
9.
【答案】
B
【解答】
∵
原式
∴
当=,即=时
代数式的值最小,为即
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
)
10.
【答案】
【解答】
,不是最简二次根式;
,不是最简二次根式;
,不是最简二次根式;
,是最简二次根式;
11.
【答案】
【解答】
解:
,
故答案为:.
12.
【答案】
【解答】
解:∵
等式成立,
∴
,且;
解得.
故答案为:.
13.
【答案】
【解答】
解:根据题意得:,
解得:.
故答案是:.
14.
【答案】
【解答】
解:此矩形的面积,
,
,
.
故答案为:.
15.
【答案】
【解答】
略
16.
【答案】
【解答】
此题暂无解答
17.
【答案】
【解答】
原式=
=
=.
18.
【答案】
【解答】
解:原式.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
∵
,,
∴
=.
∵
=,=,
∴
=
=
=.
【解答】
∵
,,
∴
=.
∵
=,=,
∴
=
=
=.
20.
【答案】
解:∵
,
∴
,
∴
,
故.
【解答】
解:∵
,
∴
,
∴
,
故.
21.
【答案】
的值为.
【解答】
解:∵
最简二次根式与是同类二次根式,
∴
,
解得:,
22.
【答案】
解:;
;
;
;
;
;
;
∵
,
∴
.
【解答】
解:;
;
;
;
;
;
;
∵
,
∴
.
23.
【答案】
解:(1)原式;
(2)原式;
(3)原式;
(4)原式.
【解答】
解:(1)原式;
(2)原式;
(3)原式;
(4)原式.
24.
【答案】
原式=;
原式=
=
=;
原式=;
原式.
【解答】
原式=;
原式=
=
=;
原式=;
原式.
25.
【答案】
由题意可得;
由(1)可得:.
【解答】
由题意可得;
由(1)可得:.
二次根式
单元测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
1.
化简的结果是?
?
?
?
A.
B.
C.
D.
?
2.
给出下列各数:①②③④,其中是方程的解的个数有(
)
A.个
B.个
C.个
D.个
?
3.
下列二次根式中,最简二次根式是(?
?
?
?
)
A.
B.
C.
D.
?
4.
化简的结果为(
)
A.
B.
C.
D.
?
5.
已知,,则代数式的值为(
)
A.
B.
C.
D.
?
6.
化简二次根式的正确结果是???
A.
B.
C.
D.
?
7.
化简+-的结果为??????
A.
B.
C.
D.
?8.
下列计算正确的是(
)
A.
B.=
C.=
D.=
?
9.
已知为实数,则代数式的最小值为(
)
A.
B.
C.
D.
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
10.
在中,是最简二次根式的是________.
?
11.
计算的结果等于________.
?
12.
若等式成立,则的取值范围是________.
?
13.
在实数范围内,使二次根式有意义的的取值范围是________.
?
14.
若矩形的长为,宽为,则此矩形的面积为________?.
?
15.
二次根式中的取值范围是________.
?
16.
若二次根式有意义,则的取值范围为________.
?
17.
计算________.
?
18.
化简并计算:________.(结果中分母不含根式)
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
设长方形的面积为,相邻两边分别为,
(1)已知,,求;
(2)已知=,=,求.
?
20.
已知,求的值.
?
21.
若最简二次根式与是同类二次根式,求的值.
?
22.
计算:
.
?23.
计算:
(1)
(2)
(3)
(4).
?
24.
计算.
(1).
(2).
(3).
(4).
?
25.
阅读材料,解答下列问题.
例:当时,如=则==,故此时的绝对值是它本身;
当=时,=,故此时的绝对值是零;
当时,如=则==,故此时的绝对值是它的相反数.
∴
综合起来一个数的绝对值要分三种情况,即,
这种分析方法渗透了数学的分类讨论思想.
问:(
(1))请仿照例中的分类讨论的方法,分析二次根式的各种展开的情况;
(2)猜想与的大小关系.
参考答案与试题解析
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
)
1.
【答案】
B
【解答】
解:.
故选.
2.
【答案】
A
【解答】
=,
解得;=,,
故①②③④,其中是方程的解.
3.
【答案】
A
【解答】
解:、是最简二次根式;?
、,被开方数含能开得尽方的因数,不是最简二次根式;
、,被开方数含分母,不是最简二次根式;
、,被开方数含分母,不是最简二次根式.
故选.
4.
【答案】
D
【解答】
解:∵
有意义,
∴
,
∴
,
∴
,
∴
.
故选.
5.
【答案】
B
【解答】
解:当,时,
.
故选:.
6.
【答案】
【解答】
解:…二次根式有意义,则,即
…原式
故选:.
7.
【答案】
【解答】
此题暂无解答
8.
【答案】
A
【解答】
、,故此选项正确;
、=,故此选项错误;
、=,故此选项错误;
、无法计算,故此选项错误;
9.
【答案】
B
【解答】
∵
原式
∴
当=,即=时
代数式的值最小,为即
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
)
10.
【答案】
【解答】
,不是最简二次根式;
,不是最简二次根式;
,不是最简二次根式;
,是最简二次根式;
11.
【答案】
【解答】
解:
,
故答案为:.
12.
【答案】
【解答】
解:∵
等式成立,
∴
,且;
解得.
故答案为:.
13.
【答案】
【解答】
解:根据题意得:,
解得:.
故答案是:.
14.
【答案】
【解答】
解:此矩形的面积,
,
,
.
故答案为:.
15.
【答案】
【解答】
略
16.
【答案】
【解答】
此题暂无解答
17.
【答案】
【解答】
原式=
=
=.
18.
【答案】
【解答】
解:原式.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
∵
,,
∴
=.
∵
=,=,
∴
=
=
=.
【解答】
∵
,,
∴
=.
∵
=,=,
∴
=
=
=.
20.
【答案】
解:∵
,
∴
,
∴
,
故.
【解答】
解:∵
,
∴
,
∴
,
故.
21.
【答案】
的值为.
【解答】
解:∵
最简二次根式与是同类二次根式,
∴
,
解得:,
22.
【答案】
解:;
;
;
;
;
;
;
∵
,
∴
.
【解答】
解:;
;
;
;
;
;
;
∵
,
∴
.
23.
【答案】
解:(1)原式;
(2)原式;
(3)原式;
(4)原式.
【解答】
解:(1)原式;
(2)原式;
(3)原式;
(4)原式.
24.
【答案】
原式=;
原式=
=
=;
原式=;
原式.
【解答】
原式=;
原式=
=
=;
原式=;
原式.
25.
【答案】
由题意可得;
由(1)可得:.
【解答】
由题意可得;
由(1)可得:.
