苏科版九年级数学上册培优圆周角定理练习(word版含答案)
文档属性
| 名称 | 苏科版九年级数学上册培优圆周角定理练习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 20:46:42 | ||
图片预览



文档简介
第10讲 圆周角定理
【思维入门】
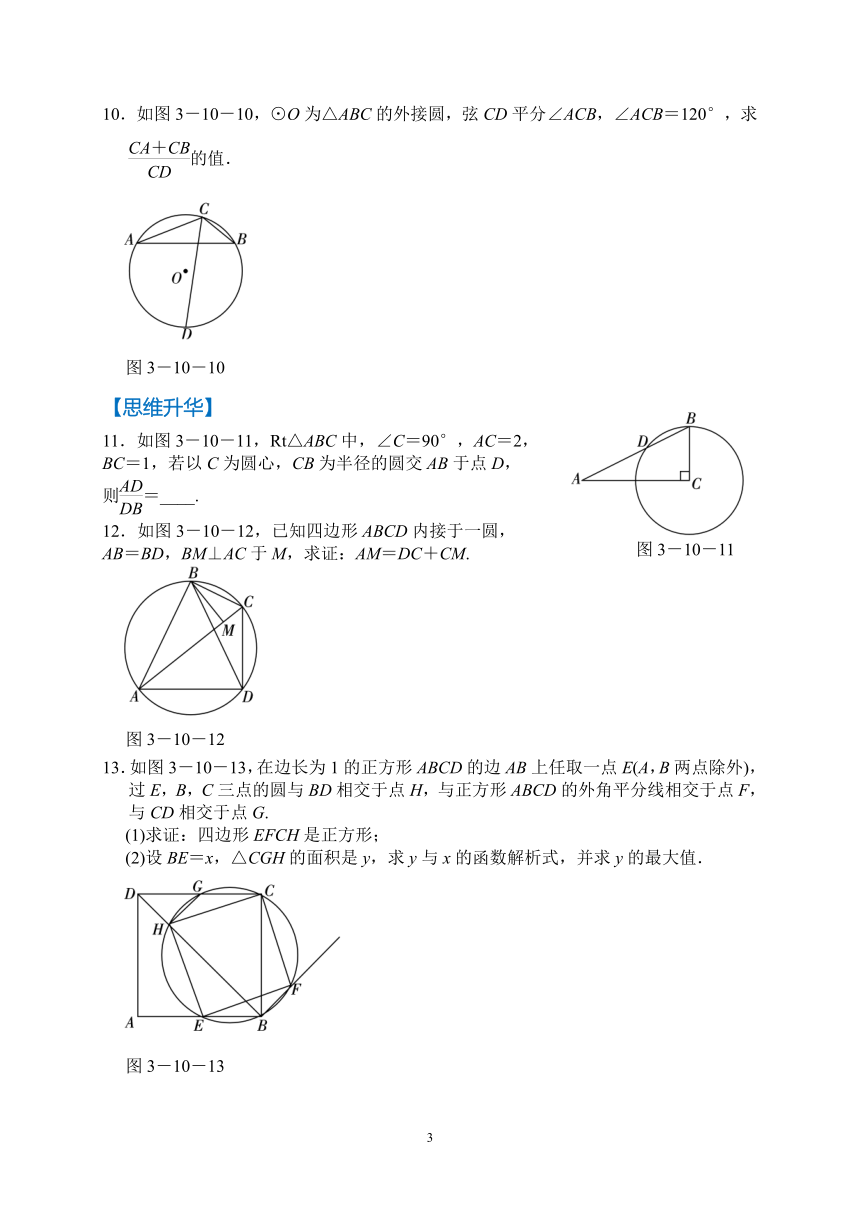
如图3-10-1,CD是⊙O的直径,弦AB⊥CD于E,
连结BC,BD,下列结论中不一定正确的是
( )
A.AE=BE
B.=
C.OE=DE
D.∠DBC=90°
图3-10-1
图3-10-2
图3-10-3
2.如图3-10-2,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为
( )
A.
B.3
C.2
D.4
3.如图3-10-3,?ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,连结AE,∠E=36°,则∠ADC的度数是
( )
A.44°
B.54°
C.72°
D.53°
4.如图3-10-4,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB等于
( )
A.55°
B.60°
C.65°
D.70°
图3-10-4
图3-10-5
5.如图3-10-5,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连结OD,OE,若∠A=65°,则∠DOE=____°.
6.如图3-10-6,点A,B,D,E在圆上,弦AE的延长线与弦BD的延长线相交于点C.给出下列三个条件:(1)AB是圆的直径;(2)D是BC的中点;(3)AB=AC.
请在上述条件中选择两个作为已知条件,第三个作为结论,写出一个你认为正确的命题,并加以证明.
图3-10-6
【思维拓展】
7.如图3-10-7,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为
( )
A.2
B.8
C.2
D.2
图3-10-7
图3-10-8
8.如图3-10-8,半圆O的直径AB=10
cm,弦AC=6
cm,AD平分∠BAC,则AD的长为
( )
A.4
cm
B.3
cm
C.5
cm
D.4
cm
9.如图3-10-9,已知在△ABC中,AB>AC,∠A的外角平分线交△ABC的外接圆于点E,过E作EF⊥AB,垂足为F.求证:AB-AC=2AF.
图3-10-9
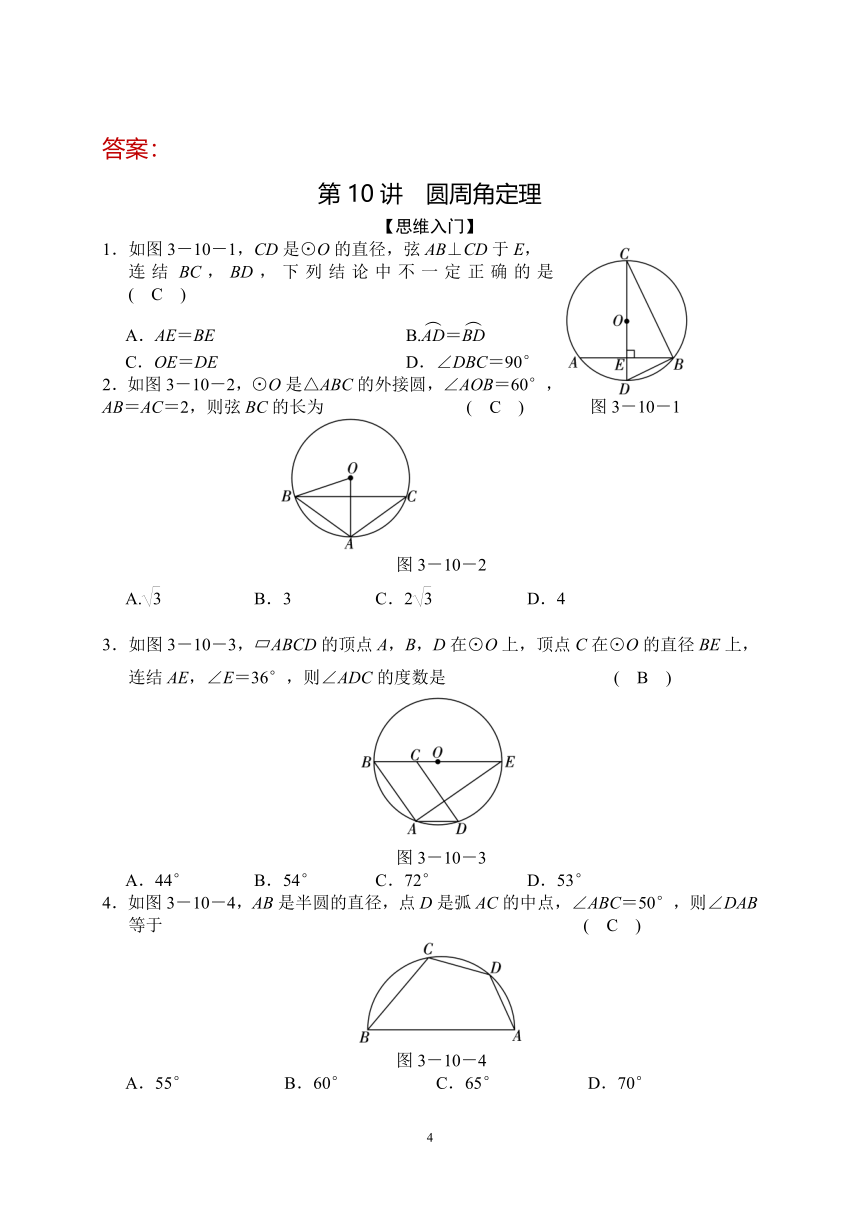
10.如图3-10-10,⊙O为△ABC的外接圆,弦CD平分∠ACB,∠ACB=120°,求的值.
图3-10-10
【思维升华】
11.如图3-10-11,Rt△ABC中,∠C=90°,AC=2,
BC=1,若以C为圆心,CB为半径的圆交AB于点D,
则=____.
12.如图3-10-12,已知四边形ABCD内接于一圆,
AB=BD,BM⊥AC于M,求证:AM=DC+CM.
图3-10-12
13.如图3-10-13,在边长为1的正方形ABCD的边AB上任取一点E(A,B两点除外),过E,B,C三点的圆与BD相交于点H,与正方形ABCD的外角平分线相交于点F,与CD相交于点G.
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CGH的面积是y,求y与x的函数解析式,并求y的最大值.
图3-10-13
答案:
第10讲 圆周角定理
【思维入门】
如图3-10-1,CD是⊙O的直径,弦AB⊥CD于E,
连结BC,BD,下列结论中不一定正确的是
( C )
A.AE=BE
B.=
C.OE=DE
D.∠DBC=90°
2.如图3-10-2,⊙O是△ABC的外接圆,∠AOB=60°,
AB=AC=2,则弦BC的长为
( C )
图3-10-2
A.
B.3
C.2
D.4
3.如图3-10-3,?ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,连结AE,∠E=36°,则∠ADC的度数是
( B )
图3-10-3
A.44°
B.54°
C.72°
D.53°
4.如图3-10-4,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB等于
( C )
图3-10-4
A.55°
B.60°
C.65°
D.70°
【解析】
连结BD,如答图,
第4题答图
∵点D是AC弧的中点,
即=,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,∴∠DAB=90°-25°=65°.
5.如图3-10-5,以△ABC的边BC为直径的⊙O分别交
AB,AC于点D,E,连结OD,OE,若∠A=65°,则∠DOE
=__50__°.
6.如图3-10-6,点A,B,D,E在圆上,弦AE的延长线
与弦BD的延长线相交于点C.
给出下列三个条件:(1)AB是圆的直径;(2)D是BC的中点;(3)AB=AC.
请在上述条件中选择两个作为已知条件,第三个作为结论,写出一个你认为正确的命题,并加以证明.
图3-10-6
解:(1)(2)为已知条件,(3)为结论.
证明:如答图,连结AD,
第6题答图
∵AB是圆的直径,
∴AD⊥BC,
∵D是BC的中点,
∴AD垂直平分BC,
∴AB=AC.
(1)(3)作为条件,(2)作为结论,
证明:如答图,连结AD,
∵AB是圆的直径,∴AD⊥BC,
∵AB=AC,∴D是BC的中点(等腰三角形三线合一).
(2)(3)作为条件,(1)作为结论.
证明:如答图,连结AD,
∵AB=AC,D是BC的中点,∴AD⊥BC,
∴AB是圆的直径.
【思维拓展】
7.如图3-10-7,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为
( D )
图3-10-7
A.2
B.8
C.2
D.2
【解析】
∵⊙O的半径OD⊥弦AB于点C,AB=8,
∴AC=AB=4,
设⊙O的半径为r,则OC=r-2,
在Rt△AOC中,
∵AC=4,OC=r-2,
∴OA2=AC2+OC2,即r2=42+(r-2)2,解得r=5,
∴AE=2r=10,
连结BE,如答图,
第7题答图
∵AE是⊙O的直径,∴∠ABE=90°,
在Rt△ABE中,
∵AE=10,AB=8,
∴BE===6,
在Rt△BCE中,
∵BE=6,BC=4,
∴CE===2.
故选D.
8.如图3-10-8,半圆O的直径AB=10
cm,弦AC
=6
cm,AD平分∠BAC,则AD的长为
( A )
A.4
cm
B.3
cm
C.5
cm
D.4
cm
【解析】
如答图,连结OD,OC,作DE⊥AB于E,OF⊥AC于F,
∵∠CAD=∠BAD(角平分线的性质),
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△ODE,
∴OE=AF=AC=3
cm,
在Rt△DOE中,DE==4
cm,
在Rt△ADE中,AD==4
cm.
故选A.
9.如图3-10-9,已知在△ABC中,AB>AC,∠A的外角平分线交△ABC的外接圆于点E,过E作EF⊥AB,垂足为F.求证:AB-AC=2AF.
图3-10-9
证明:如答图,在AB上取D使FD=AF,连结ED并延长交圆于G,连结BG,
第9题答图
则有∠1=∠2=∠3,∠1=∠G.
∴∠3=∠G,∴BG=BD,
又∵∠BAC=180°-2∠1=180°-(∠1+∠2)=∠AEG,
∴=,∴=,即AC=BG.
∴AB-AC=AB-BD=AD=2AF.
10.如图3-10-10,⊙O为△ABC的外接圆,弦CD平分∠ACB,∠ACB=120°,求的值.
图3-10-10
解:如答图,连结AD,DB,作BE∥CD交AC延长线于E.
第10题答图
∵CD平分∠ACB,∠ACB=120°,
∴∠E=∠ACD=60°,∠ECB=60°,=,
∴△BEC为等边三角形,AD=BD,
∴BE=EC=CB,
∵∠ADB=180°-∠ACB=∠ECB=60°,AD=BD,
∴△ADB为等边三角形,
∵∠EBC=∠ABD=60°,
∴AD=DB=AB,
在△ABE与△DBC中,
∴△ABE≌△DBC(SAS),
∴CD=AE=CA+CE=CA+CB,
∴=1.
【思维升华】
11.如图3-10-11,Rt△ABC中,∠C=90°,AC=2,
BC=1,若以C为圆心,CB为半径的圆交AB于点D,
则=____.
12.如图3-10-12,已知四边形ABCD内接于一圆,
AB=BD,BM⊥AC于M,求证:AM=DC+CM.
图3-10-12
证明:在MA上截取ME=MC,连结BE,如答图,
∵BM⊥AC,而ME=MC,
∴BE=BC,∴∠BEC=∠BCE,
∵AB=BD,∴∠ADB=∠BAD,
第12题答图
而∠ADB=∠BCE,
∴∠BEC=∠BAD,
又∵∠BCD+∠BAD=180°,∠BEA+∠BEC=180°,
∴∠BEA=∠BCD,
而∠BAE=∠BDC,AB=BD,
∴△ABE≌△DBC,∴AE=DC,
∴AM=AE+ME=DC+CM.
13.如图3-10-13,在边长为1的正方形ABCD的边AB上任取一点E(A,B两点除外),过E,B,C三点的圆与BD相交于点H,与正方形ABCD的外角平分线相交于点F,与CD相交于点G.
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CGH的面积是y,求y与x的函数解析式,并求y的最大值.
图3-10-13
解:(1)∵
E,B,C,H,F在同一圆上,且∠EBC=90°,
∴
∠EHC=90°,∠EFC=90°.
又∵∠FBC=∠HBC=45°,∴
CF=CH.
∵∠HBF+∠HCF=180°,
∴∠HCF=90°.
∴
四边形EFCH是正方形.
(2)∵
∠GHB+∠GCB=180°,
∴∠GHB=90°,由(1)知∠CHE=90°,
∴∠CHG+∠CHB=∠EHB+∠CHB.
∴∠CHG=∠EHB.
∴CG=BE=x,∴DG=DC-CG=1-x.
∴△CGH
中,CG边上是高为DG=(1-x).
∴
y=x.(1-x)=-+.
当x=时,y有最大值.
【思维入门】
如图3-10-1,CD是⊙O的直径,弦AB⊥CD于E,
连结BC,BD,下列结论中不一定正确的是
( )
A.AE=BE
B.=
C.OE=DE
D.∠DBC=90°
图3-10-1
图3-10-2
图3-10-3
2.如图3-10-2,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为
( )
A.
B.3
C.2
D.4
3.如图3-10-3,?ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,连结AE,∠E=36°,则∠ADC的度数是
( )
A.44°
B.54°
C.72°
D.53°
4.如图3-10-4,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB等于
( )
A.55°
B.60°
C.65°
D.70°
图3-10-4
图3-10-5
5.如图3-10-5,以△ABC的边BC为直径的⊙O分别交AB,AC于点D,E,连结OD,OE,若∠A=65°,则∠DOE=____°.
6.如图3-10-6,点A,B,D,E在圆上,弦AE的延长线与弦BD的延长线相交于点C.给出下列三个条件:(1)AB是圆的直径;(2)D是BC的中点;(3)AB=AC.
请在上述条件中选择两个作为已知条件,第三个作为结论,写出一个你认为正确的命题,并加以证明.
图3-10-6
【思维拓展】
7.如图3-10-7,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为
( )
A.2
B.8
C.2
D.2
图3-10-7
图3-10-8
8.如图3-10-8,半圆O的直径AB=10
cm,弦AC=6
cm,AD平分∠BAC,则AD的长为
( )
A.4
cm
B.3
cm
C.5
cm
D.4
cm
9.如图3-10-9,已知在△ABC中,AB>AC,∠A的外角平分线交△ABC的外接圆于点E,过E作EF⊥AB,垂足为F.求证:AB-AC=2AF.
图3-10-9
10.如图3-10-10,⊙O为△ABC的外接圆,弦CD平分∠ACB,∠ACB=120°,求的值.
图3-10-10
【思维升华】
11.如图3-10-11,Rt△ABC中,∠C=90°,AC=2,
BC=1,若以C为圆心,CB为半径的圆交AB于点D,
则=____.
12.如图3-10-12,已知四边形ABCD内接于一圆,
AB=BD,BM⊥AC于M,求证:AM=DC+CM.
图3-10-12
13.如图3-10-13,在边长为1的正方形ABCD的边AB上任取一点E(A,B两点除外),过E,B,C三点的圆与BD相交于点H,与正方形ABCD的外角平分线相交于点F,与CD相交于点G.
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CGH的面积是y,求y与x的函数解析式,并求y的最大值.
图3-10-13
答案:
第10讲 圆周角定理
【思维入门】
如图3-10-1,CD是⊙O的直径,弦AB⊥CD于E,
连结BC,BD,下列结论中不一定正确的是
( C )
A.AE=BE
B.=
C.OE=DE
D.∠DBC=90°
2.如图3-10-2,⊙O是△ABC的外接圆,∠AOB=60°,
AB=AC=2,则弦BC的长为
( C )
图3-10-2
A.
B.3
C.2
D.4
3.如图3-10-3,?ABCD的顶点A,B,D在⊙O上,顶点C在⊙O的直径BE上,连结AE,∠E=36°,则∠ADC的度数是
( B )
图3-10-3
A.44°
B.54°
C.72°
D.53°
4.如图3-10-4,AB是半圆的直径,点D是弧AC的中点,∠ABC=50°,则∠DAB等于
( C )
图3-10-4
A.55°
B.60°
C.65°
D.70°
【解析】
连结BD,如答图,
第4题答图
∵点D是AC弧的中点,
即=,
∴∠ABD=∠CBD,
而∠ABC=50°,
∴∠ABD=×50°=25°,
∵AB是半圆的直径,
∴∠ADB=90°,∴∠DAB=90°-25°=65°.
5.如图3-10-5,以△ABC的边BC为直径的⊙O分别交
AB,AC于点D,E,连结OD,OE,若∠A=65°,则∠DOE
=__50__°.
6.如图3-10-6,点A,B,D,E在圆上,弦AE的延长线
与弦BD的延长线相交于点C.
给出下列三个条件:(1)AB是圆的直径;(2)D是BC的中点;(3)AB=AC.
请在上述条件中选择两个作为已知条件,第三个作为结论,写出一个你认为正确的命题,并加以证明.
图3-10-6
解:(1)(2)为已知条件,(3)为结论.
证明:如答图,连结AD,
第6题答图
∵AB是圆的直径,
∴AD⊥BC,
∵D是BC的中点,
∴AD垂直平分BC,
∴AB=AC.
(1)(3)作为条件,(2)作为结论,
证明:如答图,连结AD,
∵AB是圆的直径,∴AD⊥BC,
∵AB=AC,∴D是BC的中点(等腰三角形三线合一).
(2)(3)作为条件,(1)作为结论.
证明:如答图,连结AD,
∵AB=AC,D是BC的中点,∴AD⊥BC,
∴AB是圆的直径.
【思维拓展】
7.如图3-10-7,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为
( D )
图3-10-7
A.2
B.8
C.2
D.2
【解析】
∵⊙O的半径OD⊥弦AB于点C,AB=8,
∴AC=AB=4,
设⊙O的半径为r,则OC=r-2,
在Rt△AOC中,
∵AC=4,OC=r-2,
∴OA2=AC2+OC2,即r2=42+(r-2)2,解得r=5,
∴AE=2r=10,
连结BE,如答图,
第7题答图
∵AE是⊙O的直径,∴∠ABE=90°,
在Rt△ABE中,
∵AE=10,AB=8,
∴BE===6,
在Rt△BCE中,
∵BE=6,BC=4,
∴CE===2.
故选D.
8.如图3-10-8,半圆O的直径AB=10
cm,弦AC
=6
cm,AD平分∠BAC,则AD的长为
( A )
A.4
cm
B.3
cm
C.5
cm
D.4
cm
【解析】
如答图,连结OD,OC,作DE⊥AB于E,OF⊥AC于F,
∵∠CAD=∠BAD(角平分线的性质),
∴∠DOB=∠OAC=2∠BAD,
∴△AOF≌△ODE,
∴OE=AF=AC=3
cm,
在Rt△DOE中,DE==4
cm,
在Rt△ADE中,AD==4
cm.
故选A.
9.如图3-10-9,已知在△ABC中,AB>AC,∠A的外角平分线交△ABC的外接圆于点E,过E作EF⊥AB,垂足为F.求证:AB-AC=2AF.
图3-10-9
证明:如答图,在AB上取D使FD=AF,连结ED并延长交圆于G,连结BG,
第9题答图
则有∠1=∠2=∠3,∠1=∠G.
∴∠3=∠G,∴BG=BD,
又∵∠BAC=180°-2∠1=180°-(∠1+∠2)=∠AEG,
∴=,∴=,即AC=BG.
∴AB-AC=AB-BD=AD=2AF.
10.如图3-10-10,⊙O为△ABC的外接圆,弦CD平分∠ACB,∠ACB=120°,求的值.
图3-10-10
解:如答图,连结AD,DB,作BE∥CD交AC延长线于E.
第10题答图
∵CD平分∠ACB,∠ACB=120°,
∴∠E=∠ACD=60°,∠ECB=60°,=,
∴△BEC为等边三角形,AD=BD,
∴BE=EC=CB,
∵∠ADB=180°-∠ACB=∠ECB=60°,AD=BD,
∴△ADB为等边三角形,
∵∠EBC=∠ABD=60°,
∴AD=DB=AB,
在△ABE与△DBC中,
∴△ABE≌△DBC(SAS),
∴CD=AE=CA+CE=CA+CB,
∴=1.
【思维升华】
11.如图3-10-11,Rt△ABC中,∠C=90°,AC=2,
BC=1,若以C为圆心,CB为半径的圆交AB于点D,
则=____.
12.如图3-10-12,已知四边形ABCD内接于一圆,
AB=BD,BM⊥AC于M,求证:AM=DC+CM.
图3-10-12
证明:在MA上截取ME=MC,连结BE,如答图,
∵BM⊥AC,而ME=MC,
∴BE=BC,∴∠BEC=∠BCE,
∵AB=BD,∴∠ADB=∠BAD,
第12题答图
而∠ADB=∠BCE,
∴∠BEC=∠BAD,
又∵∠BCD+∠BAD=180°,∠BEA+∠BEC=180°,
∴∠BEA=∠BCD,
而∠BAE=∠BDC,AB=BD,
∴△ABE≌△DBC,∴AE=DC,
∴AM=AE+ME=DC+CM.
13.如图3-10-13,在边长为1的正方形ABCD的边AB上任取一点E(A,B两点除外),过E,B,C三点的圆与BD相交于点H,与正方形ABCD的外角平分线相交于点F,与CD相交于点G.
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CGH的面积是y,求y与x的函数解析式,并求y的最大值.
图3-10-13
解:(1)∵
E,B,C,H,F在同一圆上,且∠EBC=90°,
∴
∠EHC=90°,∠EFC=90°.
又∵∠FBC=∠HBC=45°,∴
CF=CH.
∵∠HBF+∠HCF=180°,
∴∠HCF=90°.
∴
四边形EFCH是正方形.
(2)∵
∠GHB+∠GCB=180°,
∴∠GHB=90°,由(1)知∠CHE=90°,
∴∠CHG+∠CHB=∠EHB+∠CHB.
∴∠CHG=∠EHB.
∴CG=BE=x,∴DG=DC-CG=1-x.
∴△CGH
中,CG边上是高为DG=(1-x).
∴
y=x.(1-x)=-+.
当x=时,y有最大值.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
