苏科版九年级数学下册 第8章 统计和概率的简单应用 单元测试题(word版有答案)
文档属性
| 名称 | 苏科版九年级数学下册 第8章 统计和概率的简单应用 单元测试题(word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 711.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 20:48:23 | ||
图片预览


文档简介
第8章
统计和概率的简单应用
单元测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
针对动物园中四种可爱的动物:熊猫、孔雀、小猴、梅花鹿,想了解本班同学喜欢哪种动物的人最多,则调查对象是(
)
A.本班全体同学
B.熊猫、孔雀、小猴、梅花鹿
C.记录下来的数据
D.同学们的选票
?2.
下列事件中,发生的可能性最大的是(?
?
?
?
)
A.经过有交通信号灯的路口,遇到红灯
B.太阳从西边升起
C.从长为,,,的四条线段中任选三条,构成三角形
D.在圆中,平分弦的直径会垂直于弦
?
3.
下列事件中是必然事件的是(
)
A.明天太阳从西边升起
B.篮球队员在罚球线上投篮一次,未投中
C.抛出一枚硬币,落地后正面朝上
D.实心铁球投入水中会沉入水底
?
4.
下列调查适合用普查的是(
)
A.全市学生家庭周内收看“新闻联播”的次数
B.航天飞机的零件
C.长江中现有鱼的种类
D.一批炮弹的杀伤力
?
5.
用两把不同的钥匙去开两把不同的锁,这两把钥匙恰好能打开这两把锁,任意取出一把钥匙和一把锁,这把钥匙恰好能打开这把锁的概率是(
)
A.
B.
C.
D.
?
6.
下列游戏公平的是(
)
A.掷一个硬币两次,出现两次正面甲胜,出现两次反面乙胜
B.掷一个硬币两次,出现一次正面甲胜,出现两次反面乙胜
C.掷一个硬币两次,至少出现一次正面甲胜,出现一次反面一次正面乙胜
D.掷一个硬币两次,出现相同面甲胜,至少出现一次正面乙胜
?
7.
要调查长乐市初三学生周日的睡眠时间,选取调查对象合适的是(
)
A.选取一个学校的学生
B.选取名男生
C.选取名女生
D.随机选取名初三学生
?8.
一个口袋中有红球、白球共只,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一只球,记下它的颜色后再放回,不断重复这一过程,共摸了次,发现有次摸到红球,则估计这个口块中有红球大约多少只?(
)
A.只
B.只
C.只
D.只
?
9.
某养猪场有头猪,从中任意抽取头猪,对它们的体重检测,知这头猪,则估计这头猪共重(
)
A.
B.
C.
D.
?
10.
一个不透明的袋中有六个完全相同的小球,把它们分别标上数字小红从中随机摸出一个小球,记下数字后放回,小丽再随机摸出摸出一个小球记下数字,则两人摸出的小球上数字之和为的倍数的概率是(?
?
?
?
)
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
11.
一个不透明的袋子中有个红球,个白球,个黑球,这些球除颜色不同外没有任何区别.随机地从这个袋子中摸出一个球,这个球为红球的概率是________.
?
12.
一个班级有人,一次数学考试中,优秀的有人.在扇形图中表示优秀的人数所占百分比的扇形的圆心角的度数是________.
?
13.
由某个总体中抽取个,个,个,个组成一个样本,那么这个样本的容量为________.
?
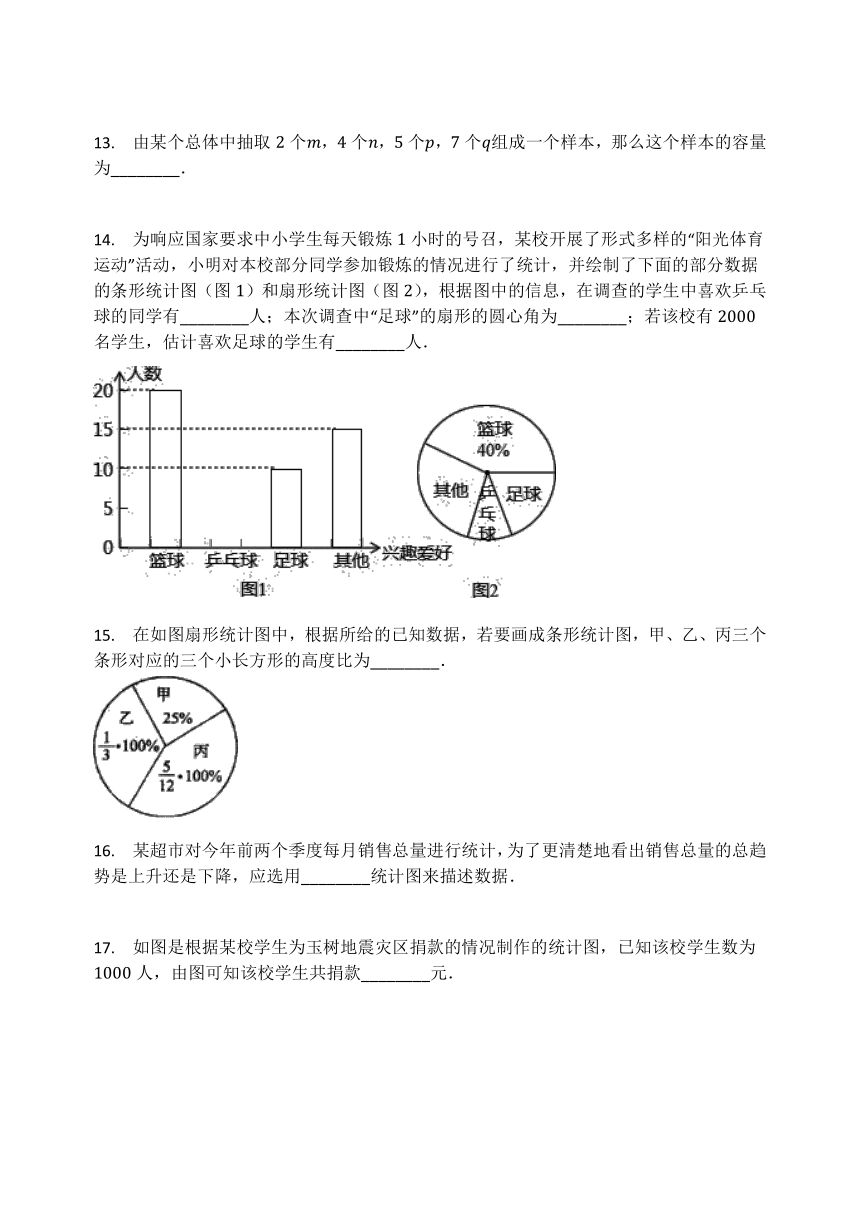
14.
为响应国家要求中小学生每天锻炼小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对本校部分同学参加锻炼的情况进行了统计,并绘制了下面的部分数据的条形统计图(图)和扇形统计图(图),根据图中的信息,在调查的学生中喜欢乒乓球的同学有________人;本次调查中“足球”的扇形的圆心角为________;若该校有名学生,估计喜欢足球的学生有________人.
15.
在如图扇形统计图中,根据所给的已知数据,若要画成条形统计图,甲、乙、丙三个条形对应的三个小长方形的高度比为________.
?
16.
某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用________统计图来描述数据.
?
17.
如图是根据某校学生为玉树地震灾区捐款的情况制作的统计图,已知该校学生数为人,由图可知该校学生共捐款________元.
?
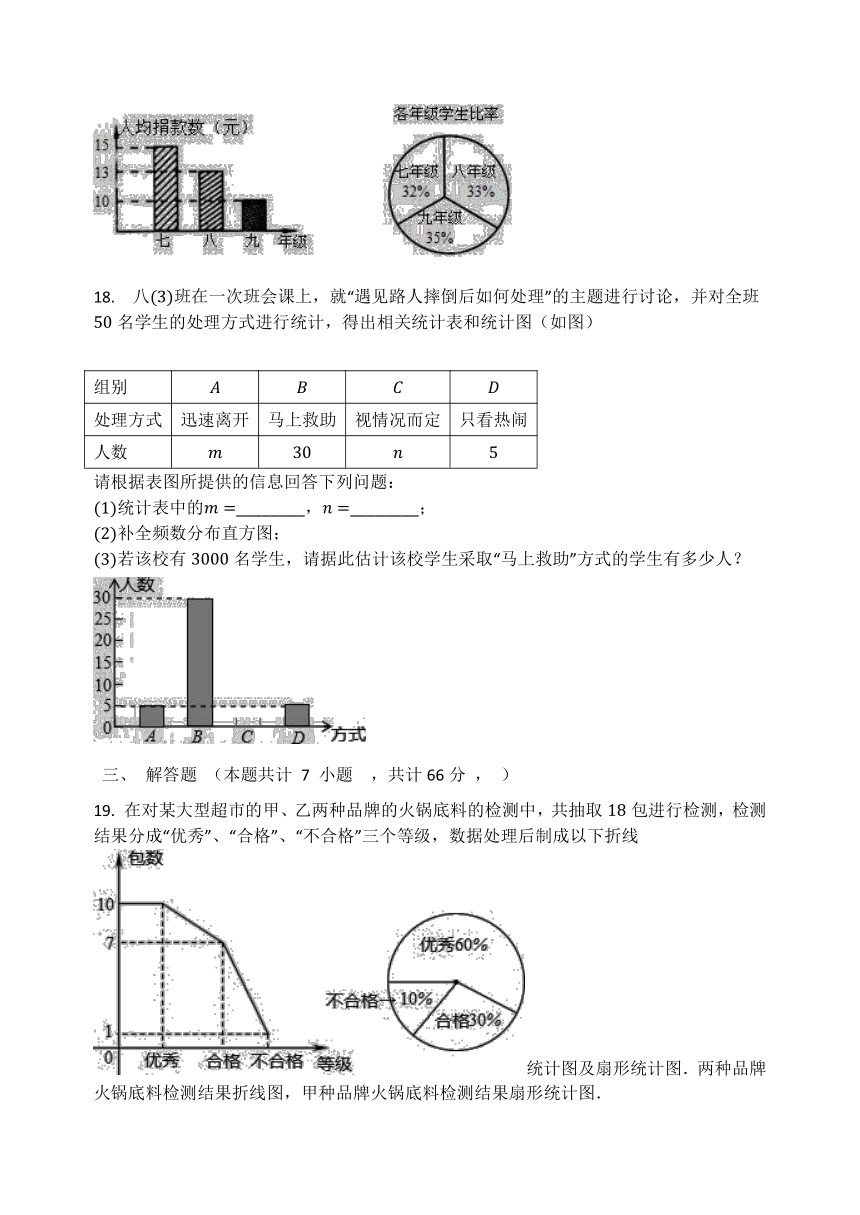
18.
八班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班名学生的处理方式进行统计,得出相关统计表和统计图(如图)
组别
处理方式
迅速离开
马上救助
视情况而定
只看热闹
人数
请根据表图所提供的信息回答下列问题:
统计表中的________,________;
补全频数分布直方图;
若该校有名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
在对某大型超市的甲、乙两种品牌的火锅底料的检测中,共抽取包进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以下折线统计图及扇形统计图.两种品牌火锅底料检测结果折线图,甲种品牌火锅底料检测结果扇形统计图.
(1)甲、乙两种火锅底料各被抽取了多少包用于检测?
(2)在该超购买甲、乙两种品牌火锅底料各一包,请你用树状图或表格方式估计能买到均为“合格”等级的概率是多少?
?
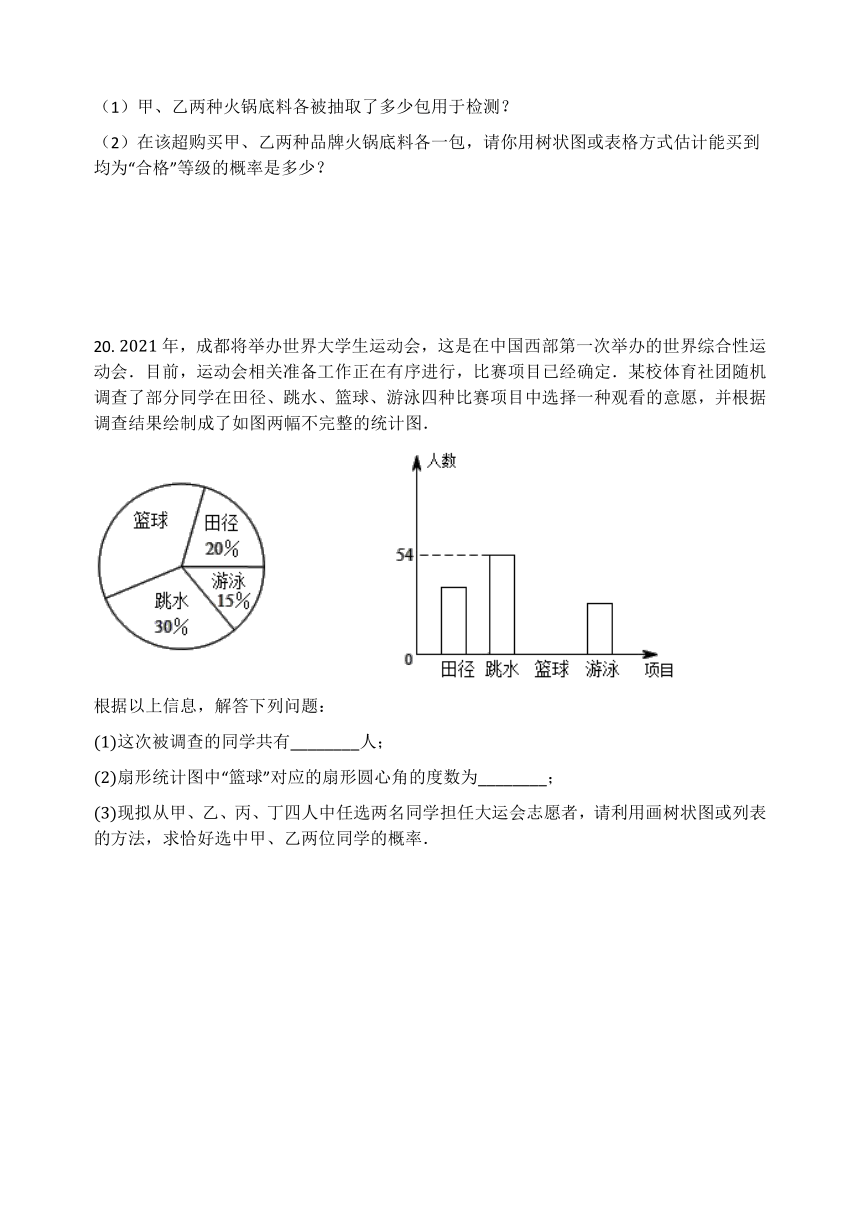
20.
年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会.目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机调查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了如图两幅不完整的统计图.
根据以上信息,解答下列问题:
这次被调查的同学共有________人;
扇形统计图中“篮球”对应的扇形圆心角的度数为________;
现拟从甲、乙、丙、丁四人中任选两名同学担任大运会志愿者,请利用画树状图或列表的方法,求恰好选中甲、乙两位同学的概率.
?
21.
某中学对九年级准备选考分钟跳绳的同学进行测试,测试结果如下表:
频数分布表
组别
跳绳(次分钟)
频数
第组
第组
第组
第组
第组
请回答下列问题:
(1)此次测试成绩的中位数落在第________组中;
(2)如果成绩达到或超过次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的________;
?
22.
胜利中学为丰富同学们的校园生活,举行“校园电视台主待人“选拔赛,现将名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:
请根据统计图的信息,解答下列问题:
补全频数分布直方图,并求扇形统计图中扇形对应的圆心角度数;
成绩在区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
23
农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了个谷穗作为样本,量得它们的长度(单位:).对样本数据适当分组后,列出了如下频数分布表:
穗长
频数
(1)请你在图,图中分别绘出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;
(3)求这块试验田里穗长在范围内的谷穗的概率.
24
武汉市号召全市人民大力推进“四城同创”,某小学名学生参加《四城同创我知晓知识问卷》活动中,为了解本次问卷成绩分布情况,从中抽取了名学生得分(得分取整数,满分分)进行统计,请根据表中提供的信息,解答下列各题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)规定把成绩在分以上的同学定为优胜者,学校准备给这些学生佩戴小红花,那么学校大约要购买多少朵小红花?
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:调查的是本班学生分别喜欢以上四种动物中的哪种动物,然后确定喜欢哪种动物的人数最多,所以是把本班全体学生作为调查对象,故正确;
故选:.
2.
【答案】
C
【解答】
解:,经过有交通信号灯的路口,遇到红灯是随机事件;
,太阳从西边升起是不可能事件;
,从长为,,,的四条线段中任选三条,构成三角形的可能性为;
,在圆中,平分(非直径)弦的直径垂直于弦是必然事件.
故选
3.
【答案】
D
【解答】
、明天太阳从西边升起是不可能事件;
、篮球队员在罚球线上投篮一次,未投中是随机事件;
、抛出一枚硬币,落地后正面朝上是随机事件;
、实心铁球投入水中会沉入水底是必然事件,
4.
【答案】
B
【解答】
解:、调查全市学生家庭周内收看“新闻联播”的次数,人数众多,应用抽样调查;
、调查航天飞机的零件,意义重大,因此应用普查;
、调查长江中现有鱼的种类,数量众多,应用抽样调查;
、调查一批炮弹的杀伤力,如果普查,所有炮弹都报废,这样就失去了实际意义,应用抽样调查;
故选:.
5.
【答案】
C
【解答】
解:设两把锁分别为:,,两把钥匙分别为:,,其中与对应,与对应,
根据题意画树状图得:
故所有可能为种,其中能打开的有两种情况,
则任意取出一把钥匙和一把锁,这把钥匙恰好能打开这把锁的概率是:.
故选:.
6.
【答案】
A
【解答】
解:∵
掷一个硬币两次,可能的结果有:正正,正反,反正,反反,
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项公平;
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项不公平;
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项不公平;
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项不公平.
故选.
7.
【答案】
D
【解答】
解:因为要调查长乐市初三学生周日的睡眠时间,所以选取调查对象是随机选取名初三学生,故选.
8.
【答案】
B
【解答】
∵
共摸了次,其中有次摸到红球,
∴
口袋中红球和总球数之比为,
∵
口袋中有红球、白球共只,
∴
估计这个口块中有红球大约有(只).
9.
【答案】
A
【解答】
解:∵
任意抽取头猪,知这头猪,
∴
估计这头猪共重.
故选.
10.
【答案】
C
【解答】
解:小丽和小红从中各摸一球,共有种情况,
其中数字之和是的倍数有共种,
故数字之和是的倍数概率为.
故选
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
解:∵
一个不透明的袋子中有个红球,个白球,个黑球,这些球除颜色不同外其他完全相同,
∴
从袋子中随机摸出一个球是球红的概率为:.
故答案为:;
12.
【答案】
【解答】
解:扇形图中表示优秀的人数所占百分比的扇形的圆心角的度数是.
故答案为:.
13.
【答案】
【解答】
解:根据样本的容量的定义可得:
这个样本的容量为:,
故答案为:.
14.
【答案】
,,
【解答】
解:调查的总人数是:(人),
则调查的学生中喜欢乒乓球的同学有(人),
本次调查中“足球”的扇形的圆心角为:,
估计喜欢足球的学生有(人).
故答案是:,,.
15.
【答案】
【解答】
解:,
故.
故答案为:.
16.
【答案】
折线
【解答】
解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
17.
【答案】
【解答】
解:元;
元;
元;
∴
该校学生共捐款元.
故答案为:.
18.
【答案】
,
【解答】
解:根据条形图可以得到:,(人);
故答案是:,;
根据求出的的值,可直接补图如下:
根据题意得:
(人).
答:该校学生采取“马上救助”方式的学生有人.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:(1),,
即甲种品牌有包,乙种品牌有包.
(2)根据折线图与扇形图可以得出:
不合格等级的有包,而且是甲种品牌火锅底料,
选取甲火锅底料一共有种可能,选取乙火锅底料一共有种可能,故所有可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的概率是:.
【解答】
解:(1),,
即甲种品牌有包,乙种品牌有包.
(2)根据折线图与扇形图可以得出:
不合格等级的有包,而且是甲种品牌火锅底料,
选取甲火锅底料一共有种可能,选取乙火锅底料一共有种可能,故所有可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的概率是:.
20.
【答案】
列表如下:
甲
乙
丙
丁
甲
一
(乙,甲)
(丙,甲)
(丁,甲)
乙
(甲,乙)
一
(丙,乙)
(丁,乙)
丙
(甲,丙)
(乙,丙)
一
(丁,丙)
丁
(甲,丁)
(乙,丁)
(丙,丁)
一
∵
共有种等可能的情况,恰好选中甲、乙两位同学的有种,
∴
恰好选中甲、乙两位同学的概率为.
【解答】
解:根据题意得:
(人).
故答案为:.
根据题意得:
.
故答案为:.
列表如下:
甲
乙
丙
丁
甲
一
(乙,甲)
(丙,甲)
(丁,甲)
乙
(甲,乙)
一
(丙,乙)
(丁,乙)
丙
(甲,丙)
(乙,丙)
一
(丁,丙)
丁
(甲,丁)
(乙,丁)
(丙,丁)
一
∵
共有种等可能的情况,恰好选中甲、乙两位同学的有种,
∴
恰好选中甲、乙两位同学的概率为.
21.
【答案】
,
不可以,选考跳绳的同学说明对跳绳比较擅长,这样一来,样本不具有随机性.所以不能代表整体的水平.
【解答】
数据个数:=,位置处于中间数是第和个,落在第小组,
=,
=;
不可以,选考跳绳的同学说明对跳绳比较擅长,这样一来,样本不具有随机性.所以不能代表整体的水平.
22.
【答案】
解:的频数为,
则的频数为,
的频数为,
补全频数分布直方图如下:
扇形统计图中扇形对应的圆心角度数为.
画树状图为:
共有种等可能的结果数,其中抽取的学生恰好是一名男生和一名女生的结果数为,
所以抽取的学生恰好是一名男生和一名女生的概率为.
【解答】
解:的频数为,
则的频数为,
的频数为,
补全频数分布直方图如下:
扇形统计图中扇形对应的圆心角度数为.
画树状图为:
共有种等可能的结果数,其中抽取的学生恰好是一名男生和一名女生的结果数为,
所以抽取的学生恰好是一名男生和一名女生的概率为.
23.
【答案】
解:(1)做出统计图,如图所示:
(2)由(1)可知谷穗长度大部分落在至之间,其它区域较少,
长度在范围内的谷穗个数最多,有个,而长度在,范围内的谷穗个数很少,总共只有个;
(3)这块试验田里穗长在范围内的谷穗的概率为.
【解答】
解:(1)做出统计图,如图所示:
(2)由(1)可知谷穗长度大部分落在至之间,其它区域较少,
长度在范围内的谷穗个数最多,有个,而长度在,范围内的谷穗个数很少,总共只有个;
(3)这块试验田里穗长在范围内的谷穗的概率为.
24
【答案】
解:组的频率,
组的频数,
的频率;
如图:
(3)从图中可以看出四五组为分以上的学生数,
∴
分以上的人数人.
【解答】
解:组的频率,
组的频数,
的频率;
如图:
(3)从图中可以看出四五组为分以上的学生数,
∴
分以上的人数人
统计和概率的简单应用
单元测试题
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
针对动物园中四种可爱的动物:熊猫、孔雀、小猴、梅花鹿,想了解本班同学喜欢哪种动物的人最多,则调查对象是(
)
A.本班全体同学
B.熊猫、孔雀、小猴、梅花鹿
C.记录下来的数据
D.同学们的选票
?2.
下列事件中,发生的可能性最大的是(?
?
?
?
)
A.经过有交通信号灯的路口,遇到红灯
B.太阳从西边升起
C.从长为,,,的四条线段中任选三条,构成三角形
D.在圆中,平分弦的直径会垂直于弦
?
3.
下列事件中是必然事件的是(
)
A.明天太阳从西边升起
B.篮球队员在罚球线上投篮一次,未投中
C.抛出一枚硬币,落地后正面朝上
D.实心铁球投入水中会沉入水底
?
4.
下列调查适合用普查的是(
)
A.全市学生家庭周内收看“新闻联播”的次数
B.航天飞机的零件
C.长江中现有鱼的种类
D.一批炮弹的杀伤力
?
5.
用两把不同的钥匙去开两把不同的锁,这两把钥匙恰好能打开这两把锁,任意取出一把钥匙和一把锁,这把钥匙恰好能打开这把锁的概率是(
)
A.
B.
C.
D.
?
6.
下列游戏公平的是(
)
A.掷一个硬币两次,出现两次正面甲胜,出现两次反面乙胜
B.掷一个硬币两次,出现一次正面甲胜,出现两次反面乙胜
C.掷一个硬币两次,至少出现一次正面甲胜,出现一次反面一次正面乙胜
D.掷一个硬币两次,出现相同面甲胜,至少出现一次正面乙胜
?
7.
要调查长乐市初三学生周日的睡眠时间,选取调查对象合适的是(
)
A.选取一个学校的学生
B.选取名男生
C.选取名女生
D.随机选取名初三学生
?8.
一个口袋中有红球、白球共只,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一只球,记下它的颜色后再放回,不断重复这一过程,共摸了次,发现有次摸到红球,则估计这个口块中有红球大约多少只?(
)
A.只
B.只
C.只
D.只
?
9.
某养猪场有头猪,从中任意抽取头猪,对它们的体重检测,知这头猪,则估计这头猪共重(
)
A.
B.
C.
D.
?
10.
一个不透明的袋中有六个完全相同的小球,把它们分别标上数字小红从中随机摸出一个小球,记下数字后放回,小丽再随机摸出摸出一个小球记下数字,则两人摸出的小球上数字之和为的倍数的概率是(?
?
?
?
)
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
11.
一个不透明的袋子中有个红球,个白球,个黑球,这些球除颜色不同外没有任何区别.随机地从这个袋子中摸出一个球,这个球为红球的概率是________.
?
12.
一个班级有人,一次数学考试中,优秀的有人.在扇形图中表示优秀的人数所占百分比的扇形的圆心角的度数是________.
?
13.
由某个总体中抽取个,个,个,个组成一个样本,那么这个样本的容量为________.
?
14.
为响应国家要求中小学生每天锻炼小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对本校部分同学参加锻炼的情况进行了统计,并绘制了下面的部分数据的条形统计图(图)和扇形统计图(图),根据图中的信息,在调查的学生中喜欢乒乓球的同学有________人;本次调查中“足球”的扇形的圆心角为________;若该校有名学生,估计喜欢足球的学生有________人.
15.
在如图扇形统计图中,根据所给的已知数据,若要画成条形统计图,甲、乙、丙三个条形对应的三个小长方形的高度比为________.
?
16.
某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用________统计图来描述数据.
?
17.
如图是根据某校学生为玉树地震灾区捐款的情况制作的统计图,已知该校学生数为人,由图可知该校学生共捐款________元.
?
18.
八班在一次班会课上,就“遇见路人摔倒后如何处理”的主题进行讨论,并对全班名学生的处理方式进行统计,得出相关统计表和统计图(如图)
组别
处理方式
迅速离开
马上救助
视情况而定
只看热闹
人数
请根据表图所提供的信息回答下列问题:
统计表中的________,________;
补全频数分布直方图;
若该校有名学生,请据此估计该校学生采取“马上救助”方式的学生有多少人?
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
在对某大型超市的甲、乙两种品牌的火锅底料的检测中,共抽取包进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以下折线统计图及扇形统计图.两种品牌火锅底料检测结果折线图,甲种品牌火锅底料检测结果扇形统计图.
(1)甲、乙两种火锅底料各被抽取了多少包用于检测?
(2)在该超购买甲、乙两种品牌火锅底料各一包,请你用树状图或表格方式估计能买到均为“合格”等级的概率是多少?
?
20.
年,成都将举办世界大学生运动会,这是在中国西部第一次举办的世界综合性运动会.目前,运动会相关准备工作正在有序进行,比赛项目已经确定.某校体育社团随机调查了部分同学在田径、跳水、篮球、游泳四种比赛项目中选择一种观看的意愿,并根据调查结果绘制成了如图两幅不完整的统计图.
根据以上信息,解答下列问题:
这次被调查的同学共有________人;
扇形统计图中“篮球”对应的扇形圆心角的度数为________;
现拟从甲、乙、丙、丁四人中任选两名同学担任大运会志愿者,请利用画树状图或列表的方法,求恰好选中甲、乙两位同学的概率.
?
21.
某中学对九年级准备选考分钟跳绳的同学进行测试,测试结果如下表:
频数分布表
组别
跳绳(次分钟)
频数
第组
第组
第组
第组
第组
请回答下列问题:
(1)此次测试成绩的中位数落在第________组中;
(2)如果成绩达到或超过次/分钟的同学可获满分,那么本次测试中获得满分的人数占参加测试人数的________;
?
22.
胜利中学为丰富同学们的校园生活,举行“校园电视台主待人“选拔赛,现将名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:
请根据统计图的信息,解答下列问题:
补全频数分布直方图,并求扇形统计图中扇形对应的圆心角度数;
成绩在区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
23
农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了个谷穗作为样本,量得它们的长度(单位:).对样本数据适当分组后,列出了如下频数分布表:
穗长
频数
(1)请你在图,图中分别绘出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;
(3)求这块试验田里穗长在范围内的谷穗的概率.
24
武汉市号召全市人民大力推进“四城同创”,某小学名学生参加《四城同创我知晓知识问卷》活动中,为了解本次问卷成绩分布情况,从中抽取了名学生得分(得分取整数,满分分)进行统计,请根据表中提供的信息,解答下列各题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)规定把成绩在分以上的同学定为优胜者,学校准备给这些学生佩戴小红花,那么学校大约要购买多少朵小红花?
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
A
【解答】
解:调查的是本班学生分别喜欢以上四种动物中的哪种动物,然后确定喜欢哪种动物的人数最多,所以是把本班全体学生作为调查对象,故正确;
故选:.
2.
【答案】
C
【解答】
解:,经过有交通信号灯的路口,遇到红灯是随机事件;
,太阳从西边升起是不可能事件;
,从长为,,,的四条线段中任选三条,构成三角形的可能性为;
,在圆中,平分(非直径)弦的直径垂直于弦是必然事件.
故选
3.
【答案】
D
【解答】
、明天太阳从西边升起是不可能事件;
、篮球队员在罚球线上投篮一次,未投中是随机事件;
、抛出一枚硬币,落地后正面朝上是随机事件;
、实心铁球投入水中会沉入水底是必然事件,
4.
【答案】
B
【解答】
解:、调查全市学生家庭周内收看“新闻联播”的次数,人数众多,应用抽样调查;
、调查航天飞机的零件,意义重大,因此应用普查;
、调查长江中现有鱼的种类,数量众多,应用抽样调查;
、调查一批炮弹的杀伤力,如果普查,所有炮弹都报废,这样就失去了实际意义,应用抽样调查;
故选:.
5.
【答案】
C
【解答】
解:设两把锁分别为:,,两把钥匙分别为:,,其中与对应,与对应,
根据题意画树状图得:
故所有可能为种,其中能打开的有两种情况,
则任意取出一把钥匙和一把锁,这把钥匙恰好能打开这把锁的概率是:.
故选:.
6.
【答案】
A
【解答】
解:∵
掷一个硬币两次,可能的结果有:正正,正反,反正,反反,
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项公平;
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项不公平;
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项不公平;
、∵
(甲胜),(乙胜),∴
(甲胜)(乙胜),故本选项不公平.
故选.
7.
【答案】
D
【解答】
解:因为要调查长乐市初三学生周日的睡眠时间,所以选取调查对象是随机选取名初三学生,故选.
8.
【答案】
B
【解答】
∵
共摸了次,其中有次摸到红球,
∴
口袋中红球和总球数之比为,
∵
口袋中有红球、白球共只,
∴
估计这个口块中有红球大约有(只).
9.
【答案】
A
【解答】
解:∵
任意抽取头猪,知这头猪,
∴
估计这头猪共重.
故选.
10.
【答案】
C
【解答】
解:小丽和小红从中各摸一球,共有种情况,
其中数字之和是的倍数有共种,
故数字之和是的倍数概率为.
故选
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
解:∵
一个不透明的袋子中有个红球,个白球,个黑球,这些球除颜色不同外其他完全相同,
∴
从袋子中随机摸出一个球是球红的概率为:.
故答案为:;
12.
【答案】
【解答】
解:扇形图中表示优秀的人数所占百分比的扇形的圆心角的度数是.
故答案为:.
13.
【答案】
【解答】
解:根据样本的容量的定义可得:
这个样本的容量为:,
故答案为:.
14.
【答案】
,,
【解答】
解:调查的总人数是:(人),
则调查的学生中喜欢乒乓球的同学有(人),
本次调查中“足球”的扇形的圆心角为:,
估计喜欢足球的学生有(人).
故答案是:,,.
15.
【答案】
【解答】
解:,
故.
故答案为:.
16.
【答案】
折线
【解答】
解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
17.
【答案】
【解答】
解:元;
元;
元;
∴
该校学生共捐款元.
故答案为:.
18.
【答案】
,
【解答】
解:根据条形图可以得到:,(人);
故答案是:,;
根据求出的的值,可直接补图如下:
根据题意得:
(人).
答:该校学生采取“马上救助”方式的学生有人.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:(1),,
即甲种品牌有包,乙种品牌有包.
(2)根据折线图与扇形图可以得出:
不合格等级的有包,而且是甲种品牌火锅底料,
选取甲火锅底料一共有种可能,选取乙火锅底料一共有种可能,故所有可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的概率是:.
【解答】
解:(1),,
即甲种品牌有包,乙种品牌有包.
(2)根据折线图与扇形图可以得出:
不合格等级的有包,而且是甲种品牌火锅底料,
选取甲火锅底料一共有种可能,选取乙火锅底料一共有种可能,故所有可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的可能是种,
则在该超购买甲、乙两种品牌火锅底料各一包,能买到均为“合格”等级的概率是:.
20.
【答案】
列表如下:
甲
乙
丙
丁
甲
一
(乙,甲)
(丙,甲)
(丁,甲)
乙
(甲,乙)
一
(丙,乙)
(丁,乙)
丙
(甲,丙)
(乙,丙)
一
(丁,丙)
丁
(甲,丁)
(乙,丁)
(丙,丁)
一
∵
共有种等可能的情况,恰好选中甲、乙两位同学的有种,
∴
恰好选中甲、乙两位同学的概率为.
【解答】
解:根据题意得:
(人).
故答案为:.
根据题意得:
.
故答案为:.
列表如下:
甲
乙
丙
丁
甲
一
(乙,甲)
(丙,甲)
(丁,甲)
乙
(甲,乙)
一
(丙,乙)
(丁,乙)
丙
(甲,丙)
(乙,丙)
一
(丁,丙)
丁
(甲,丁)
(乙,丁)
(丙,丁)
一
∵
共有种等可能的情况,恰好选中甲、乙两位同学的有种,
∴
恰好选中甲、乙两位同学的概率为.
21.
【答案】
,
不可以,选考跳绳的同学说明对跳绳比较擅长,这样一来,样本不具有随机性.所以不能代表整体的水平.
【解答】
数据个数:=,位置处于中间数是第和个,落在第小组,
=,
=;
不可以,选考跳绳的同学说明对跳绳比较擅长,这样一来,样本不具有随机性.所以不能代表整体的水平.
22.
【答案】
解:的频数为,
则的频数为,
的频数为,
补全频数分布直方图如下:
扇形统计图中扇形对应的圆心角度数为.
画树状图为:
共有种等可能的结果数,其中抽取的学生恰好是一名男生和一名女生的结果数为,
所以抽取的学生恰好是一名男生和一名女生的概率为.
【解答】
解:的频数为,
则的频数为,
的频数为,
补全频数分布直方图如下:
扇形统计图中扇形对应的圆心角度数为.
画树状图为:
共有种等可能的结果数,其中抽取的学生恰好是一名男生和一名女生的结果数为,
所以抽取的学生恰好是一名男生和一名女生的概率为.
23.
【答案】
解:(1)做出统计图,如图所示:
(2)由(1)可知谷穗长度大部分落在至之间,其它区域较少,
长度在范围内的谷穗个数最多,有个,而长度在,范围内的谷穗个数很少,总共只有个;
(3)这块试验田里穗长在范围内的谷穗的概率为.
【解答】
解:(1)做出统计图,如图所示:
(2)由(1)可知谷穗长度大部分落在至之间,其它区域较少,
长度在范围内的谷穗个数最多,有个,而长度在,范围内的谷穗个数很少,总共只有个;
(3)这块试验田里穗长在范围内的谷穗的概率为.
24
【答案】
解:组的频率,
组的频数,
的频率;
如图:
(3)从图中可以看出四五组为分以上的学生数,
∴
分以上的人数人.
【解答】
解:组的频率,
组的频数,
的频率;
如图:
(3)从图中可以看出四五组为分以上的学生数,
∴
分以上的人数人
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
