人教版九年级数学下册 27.2 ---27.3测试题(2课时 Word版 有答案)
文档属性
| 名称 | 人教版九年级数学下册 27.2 ---27.3测试题(2课时 Word版 有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 908.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 22:15:50 | ||
图片预览


文档简介
27.2
相似三角形
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如图,下列条件不能判定的是(?
?
?
?
)
A.
B.
C.
D.
?2.
如图,中,点在线段上,且,则下列结论一定正确的是(
)
A.
B.
C.
D.
?3.
如图,已知直线,直线、与直线、、分别交于点、、、、、,=,=,=,则=(
)
A.
B.
C.
D.
?
4.
两个相似三角形的对应边分别是和,它们的周长相差,则这两个三角形的周长分别是?
?
?
?
A.,
B.,
C.,
D.,
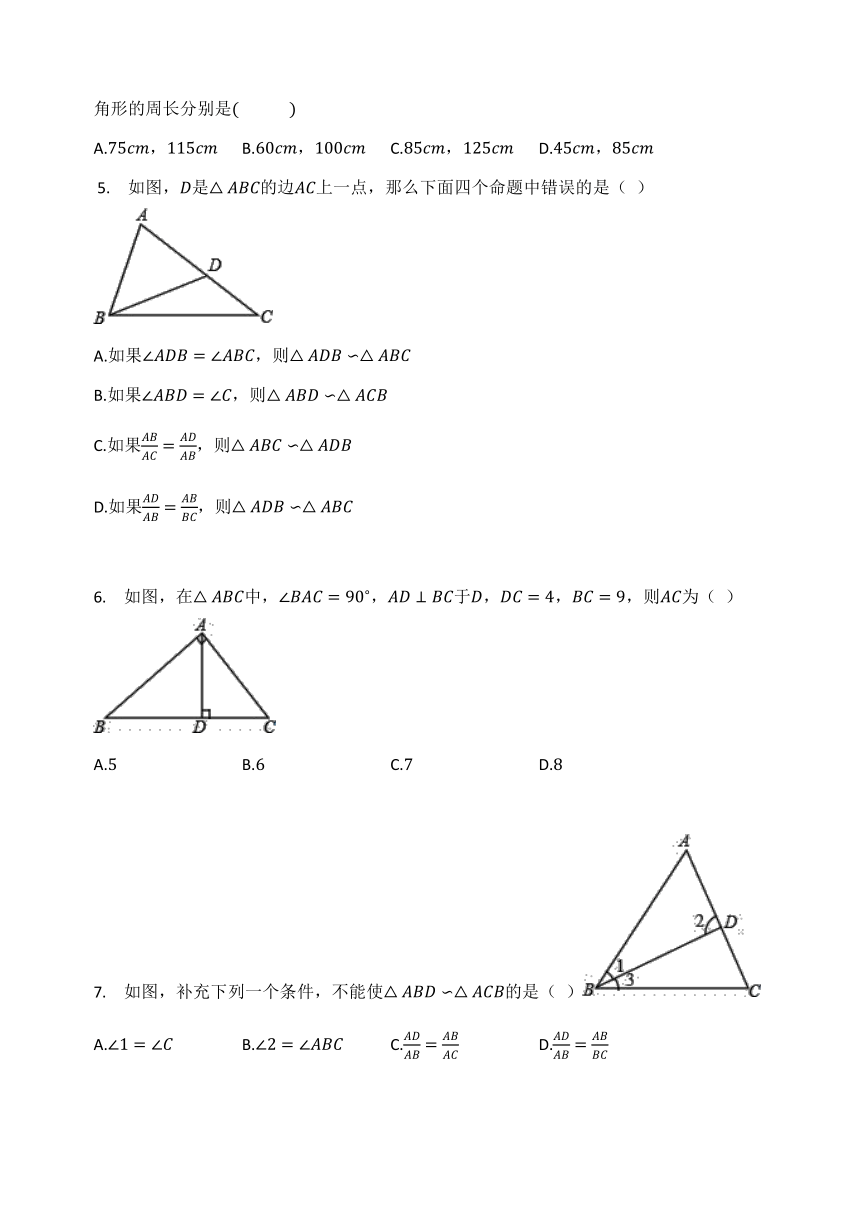
?5.
如图,是的边上一点,那么下面四个命题中错误的是(
)
A.如果,则
B.如果,则
C.如果,则
D.如果,则
?
6.
如图,在中,,于,,,则为(
)
A.
B.
C.
D.
?
7.
如图,补充下列一个条件,不能使的是(
)
A.
B.
C.
D.
?
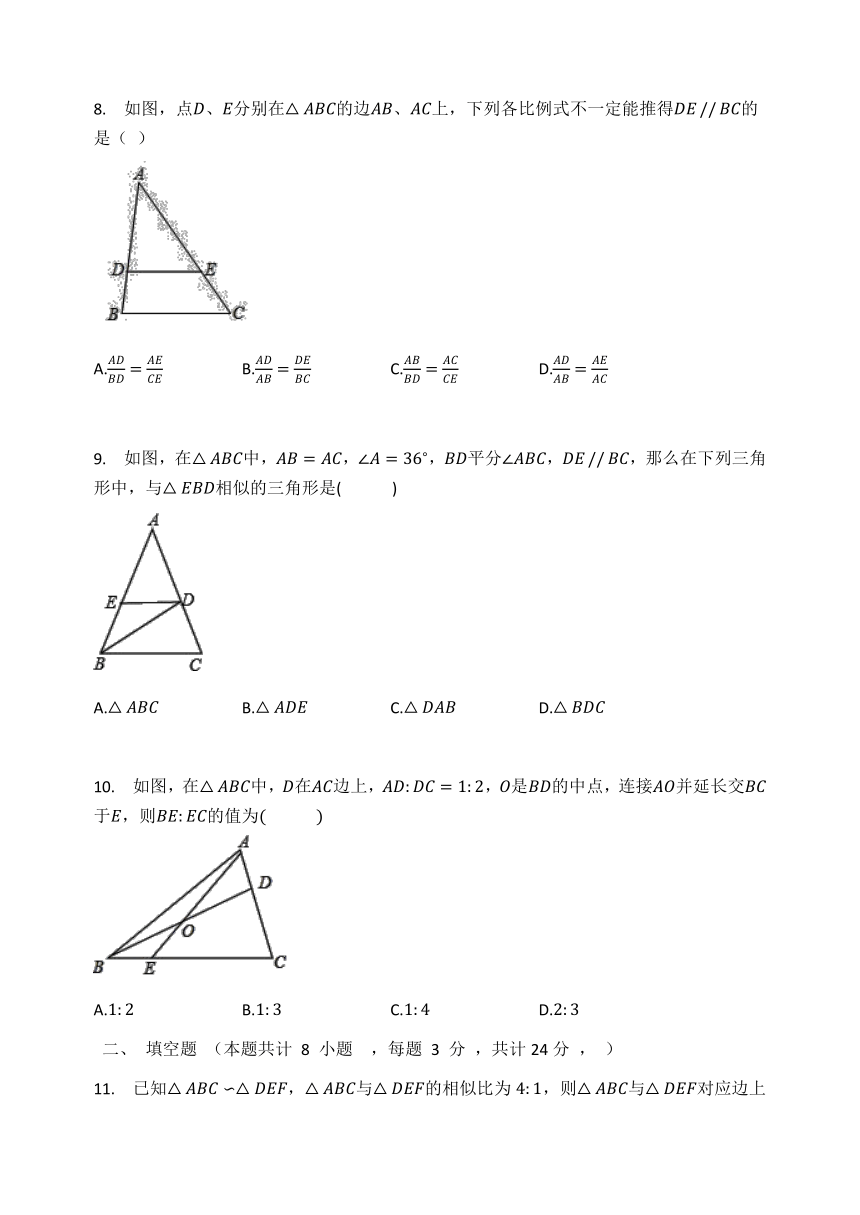
8.
如图,点、分别在的边、上,下列各比例式不一定能推得的是(
)
A.
B.
C.
D.
?
9.
如图,在中,,,平分,,那么在下列三角形中,与相似的三角形是(?
?
?
?
)
A.
B.
C.
D.
?
10.
如图,在中,在边上,,是的中点,连接并延长交于,则的值为?
?
?
?
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
11.
已知,与的相似比为,则与对应边上的高之比为________.
?
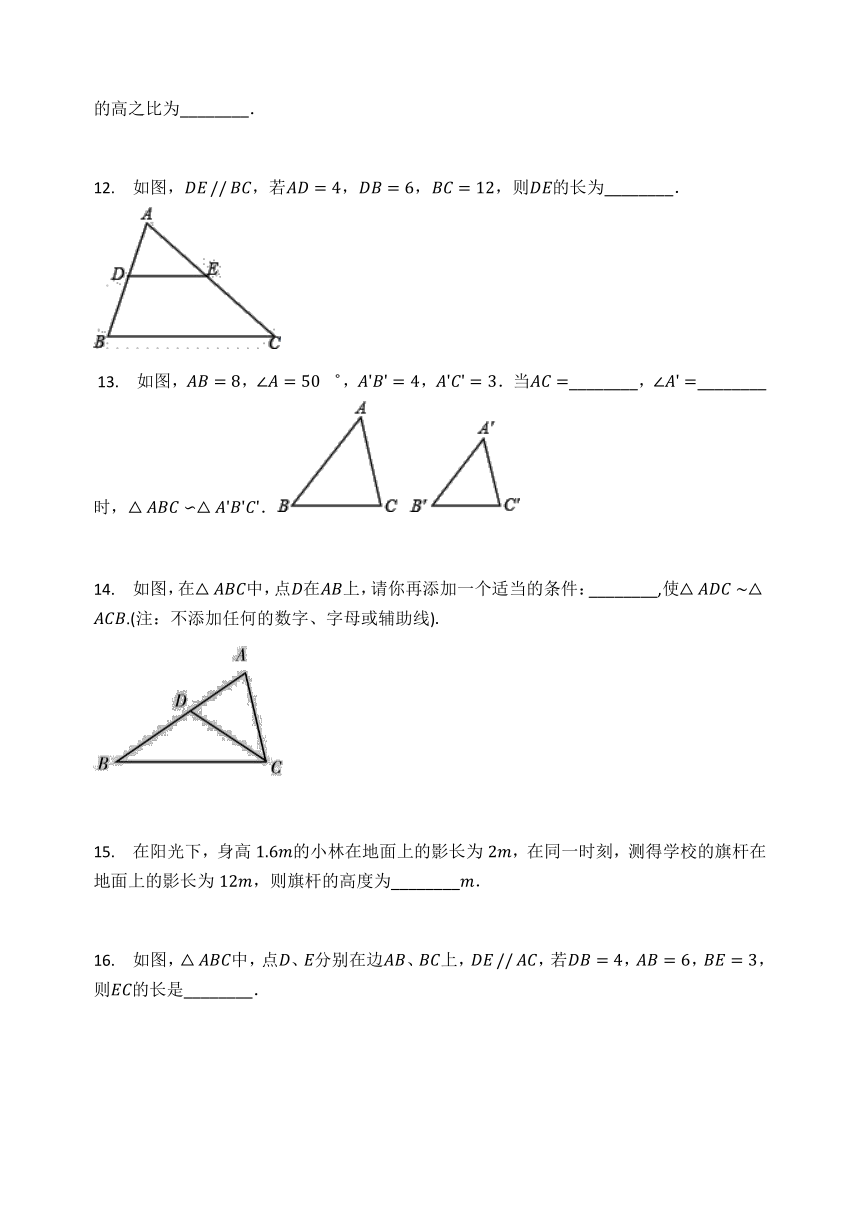
12.
如图,,若,,,则的长为________.
?13.
如图,,゜,,.当________,________时,.
?
14.
如图,在中,点在上,请你再添加一个适当的条件:________,使.(注:不添加任何的数字、字母或辅助线)
?
15.
在阳光下,身高的小林在地面上的影长为,在同一时刻,测得学校的旗杆在地面上的影长为,则旗杆的高度为________.
?
16.
如图,中,点、分别在边、上,,若,,,则的长是________.
?
17.
如图,点在的边上,请你添加一个条件,使得,这个条件可以是________.
18.
如图,某测量工作人员与标杆顶端、电视塔顶端在同一直线上,已知此人眼睛距地面米,标杆为米,且米,米,则电视塔的高________.
三、
解答题
(本题共计
7
小题
,共计60分
,
)
?
19.
如图,点为边上一点,请用尺规作图在边上找一点,使得=(保留作图痕迹,不写作法),并说明理由.
?
20.
如图,在方格纸中,以格点连线为边的三角形叫格点三角形,就是格点三角形,请在此方格纸上另画一个与相似的格点三角形,并写出它与的相似比.
?21.
如图,在中,、、分别是、上的点,且,,,,求和的长.
?
22.
如图,在正方形中,点在上,,点在上,试给出点满足什么条件时,与相似.
?
23.
已知:如图中,,.
求证:;
若,,,求的长.
?
24.
一位同学想利用有关知识测旗杆的高度,他在某一时刻测得高为的小木棒的影长为,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子,又测地面部分的影长,你能根据上述数据帮他测出旗杆的高度吗?
?
25.
中,,,为上的动点,小慧拿含角的透明三角板,使角的顶点落在点,三角板可绕点旋转.
(1)如图,当三角板的两边分别交、于点、时.求证:;
(2)将三角板绕点旋转到图情形时,三角板的两边分别交的延长线、边于点、.与还相似吗?(只需写出结论)
(3)在(2)的条件下,连结,与是否相似?若不相似,则动点运动到什么位置时,与相似?说明理由.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
解:,∵
,,∴
,故此选项不合题意;
,∵
,,∴
,故此选项不合题意;
,∵
,∴
,,,故此选项不合题意;
,∵
,∴
,不能判定,故此选项符合题意.
故选.
2.
【答案】
C
【解答】
解:∵
,
而,
∴
,
∴
,
∴
.
故选.
3.
【答案】
B
【解答】
∵
,
∴
,
∵
=,=,=,
∴
,
解得:,
∴
==.
4.
【答案】
A
【解答】
解:根据题意两个三角形的相似比是,周长比就是,
大小周长相差份,所以每份的周长是,
所以两个三角形的周长分别为,.
故选.
5.
【答案】
D
【解答】
解:中,为公共角,所以正确;
中,为公共角,所以也正确;
中对应边成比例,对应角相等,也正确;
中对应边成比例,但夹角不相等,所以错误
故选
6.
【答案】
B
【解答】
解:由射影定理得,
,
∴
.
故选:.
7.
【答案】
D
【解答】
解:∵
,,
∴
,
∴
选项不符合;
∵
,,
∴
,
∴
选项不符合;
∵
,,
∴
,
∴
选项不符合;
虽然,但,
∴
与不相似,
∴
选项符合.
故选:.
8.
【答案】
B
【解答】
∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
9.
【答案】
C
【解答】
解:∵
,,
∴
,
又∵
是的平分线,
∴
,
∵
,
∴
,
即,,
∴
.
故选.
10.
【答案】
B
【解答】
解:如图,过作,交于,
∵
是的中点,
∴
是的中点.
又,
∴
,
∴
,,
∴
,
设,,又,
∴
,,
∵
,
∴
,,
∴
,,
∴
.
故选.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
解:∵
,与的相似比为,
∴
与对应边上的高之比是,
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∴
,
∵
,,,
∴
,
∴
,
解得:.
故答案为:.
13.
【答案】
,
【解答】
解:当,时,
∵
,゜,,,
∴
,,
∴
.
故答案为,.
14.
【答案】
(答案不唯一)
【解答】
解:要使,可以添加条件.
∵
,,
∴
.
故答案为:(答案不唯一).
15.
【答案】
【解答】
解:设旗杆的高度为.
根据在同一时刻身高与影长成比例可得:,
解得:.
故答案为:.
16.
【答案】
【解答】
∵
,
∴
,
∵
,,,
∴
,
解得:,
∴
.
17.
【答案】
【解答】
在与中,为两三角形的公共角,只需再有一对应角相等即可,即,
18.
【答案】
【解答】
解:过点作,交于,交于.
由题意可得:,
∴
即,
解得:.
∴
(米).
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
【解答】
∵
=,
∴
,
∵
=,
∴
.
点
20.
【答案】
解:图形如图:相似比为.(注:答案不唯一,答对即可)
【解答】
解:图形如图:相似比为.(注:答案不唯一,答对即可)
21.
【答案】
解:∵
,
∴
,即,
∴
,
∴
,
∵
,
∴
,即,
∴
,
∴
.
【解答】
解:∵
,
∴
,即,
∴
,
∴
,
∵
,
∴
,即,
∴
,
∴
.
22.
【答案】
解:设正方形的边长为,则,
∵
,
∴
当时,,即,解得,解得;
或当时,,即,整理为,解得,
∴
当点满足或时,与相似.
【解答】
解:设正方形的边长为,则,
∵
,
∴
当时,,即,解得,解得;
或当时,,即,整理为,解得,
∴
当点满足或时,与相似.
23.
【答案】
证明:∵
,
∴
,
∵
,,,
∴
,
∴
;
解:由知,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
【解答】
证明:∵
,
∴
,
∵
,,,
∴
,
∴
;
解:由知,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
24.
【答案】
能.旗杆的高度为.
【解答】
解:∵
高为的小木棒的影长为,
∴
实际高度和影长之比为,即,
∴
落在墙上的,如果投射到地面上应该为米,即旗杆的实际影长为米,
∴
,解得,
25.
【答案】
(1)证明:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(2)解:;
理由:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(3)解:动点运动到中点位置时,与相似,
证明:同(1),可证,
得?,
而,
因此?.
又因为,
所以(两边对应成比例且夹角相等的两个三角形相似).
【解答】
(1)证明:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(2)解:;
理由:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(3)解:动点运动到中点位置时,与相似,
证明:同(1),可证,
得?,
而,
因此?.
又因为,
所以(两边对应成比例且夹角相等的两个三角形相似).
27.3
位似
(满分120分;时间:120分钟)
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
?1.
在平面直角坐标系中,,,,以原点为位似中心,将扩大到原来的倍,若点的对应点坐标为,则点的对应点的坐标为(?
?
?
?
)
A.
B.
C.
D.
?
2.
若一个多边形放大后与原多边形位似,且面积放大为原来的倍,则周长放大为原来的(
)
A.倍
B.倍
C.倍
D.倍
?
3.
在平面直角坐标系中,点,以原点为位似中心,在第一象限内把线段缩小为原来的得到线段,则点的坐标为(?
?
?
?
)
A.
B.
C.
D.
?
4.
在平面直角坐标系中,点
,将以原点为位似中心,相似比为,进行位似变换,则点的对应点的坐标是(?
?
?
?
)
A.
或
B.或
C.或
D.
或
?
5.
如图,四边形与四边形相似,位似中心是点,若=,则的值是(
)
A.
B.
C.
D.
?
6.
在平面直角坐标系中,??的三个顶点的坐标分别为??,?,以原点为位似中心,把这个三角形缩小为原来的??,得到??,则点的对应点的坐标是?
?
?
?
A.
B.
C.或
D.或
?
7.
在平面直角坐标系中,线段两个端点的坐标分别为,,若以原点为位似中心,在第一象限内将线段缩短为原来的后得到线段,则点的对应点的坐标为(
)
A.
B.
C.
D.
?
8.
把的每一个点横坐标都乘,得到,这一变换是(
)
A.位似变换
B.旋转变换
C.中心对称变换
D.轴对称变换
?
9.
如图,与是位似图形,点是位似中心,、、分别是、、的中点,则与的面积比是?
?
?
?
A.
B.
C.
D.
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
10.
四边形与四边形位似,点为位似中心.若=,则=________.
?
11.
如图,和是以点为位似中心的位似图形,已知,,,则点的对应点的坐标是________.
12.
如果两个位似图形的对应线段的长度分别为和,且面积之和为,则较小的图形的面积为________.
?
13.
如图,在
?,点、分别是,的中点,点是上一点,将沿折叠得,,交于点,当,
相似时,的长为________.
14.
?如图,与为位似图形,点是它们的位似中心,位似比是,且的面积为,那么的面积是________.
15.
已知:如图,,,的延长线交于于点,与是________图形,其中________点是位似中心.
?
16.
已知:如图,,且,则与________是位似图形,位似比为________.
?
17.
如图,已知与是以坐标原点为位似中心的位似图形,且,若点,点,则________.
?
18.
如图,点是与的位似中心,的周长为.若、、分别是线段、、的中点,则的周长为;若、、,则的周长为;…若、、,则的周长为________.(用正整数表示)
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
如图,已知是坐标原点,,的坐标分别为,.
在轴的左侧以为位似中心作的位似三角形(要求:新图与原图的相似比为
;
分别写出,的对应点,的坐标;
若线段上有一点,则点在上的对应点的坐标为________.
?
20.
如图,在网格图中,每个小正方形边长均为,点和、、三点均为格点.
(1)以为位似中心,在网格图中作,使和位似,且位似比为;
(2)连接(1)中的,求四边形的周长.(结果保留根号)
?
21.
如图,在平面直角坐标系中,、.
画出向左平移个单位长度,再向上平移个单位长度后的;
以原点为位似中心,在轴的右侧画出
的一个位似,使它与的相似比为;
判断与
是否关于某一点为位似中心的位似图形?若是,请在图中标出位似中心,并写出点的坐标.
?
22.
如图,在正方形网格中,四边形的顶点坐标分别为,,,.
以点为位似中心,在位似中心的同侧将四边形放大为原来的倍,放大后点,,的对应点分别为,,画出四边形;
求出四边形的面积.
在中,若为线段上任一点,则变化后点的对应点的坐标为(________).
?
23.
在如图所示的方格中,每个小正方形的边长均为,与是关于点为位似中心的位似图形.
在图中标出位似中心的位置,并写出点的坐标及与的位似比;
以原点为位似中心,在轴的右侧画出的另一个位似,使它与的位似比为,并写出点的对应点的坐标;
?
24.
如图中的小方格都是边长为的正方形,与是关于点为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点;
(2)求出与的位似比;
(3)以点为位似中心,在所给的网格图的右边再画一个,使它与的位似比等于.
?25.
在如图所示的方格中,的顶点坐标分别为,,,与是关于点为位似中心的位似图形.
在图中标出位似中心的位置,并写出点的坐标及与的相似比;
以原点为位似中心,在轴的左侧画出的另一个位似,使它与的位似比为,并写出点的对应点的坐标;
参考答案
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
)
1.
【答案】
B
【解答】
解:∵
以原点为位似中心,将放大为原来的倍,
点的对应点是,
则点的对应点为.
故选.
2.
【答案】
C
【解答】
解:根据题意,扩大后的多边形与原来的多边形的相似比为,
∴
它们的周长的比为,
∴
周长扩大为原来的倍.
故选:.
3.
【答案】
A
【解答】
解:在平面直角坐标系中,点,以原点为位似中心,
在第一象限内把线段缩小为原来的得到线段,
则点的对应点的坐标为,
即点坐标为.
故选.
4.
【答案】
B
【解答】
解:的一个顶点的坐标是,
以原点为位似中心相似比为,将缩小得到它的位似图形,
∴
点的坐标是:?,,
即或?.
故选
5.
【答案】
B
【解答】
∵
四边形与四边形相似,位似中心是点,=,
∴
四边形与四边形的相似比为:,
∴
=.
6.
【答案】
C
【解答】
解:∵
点,且相似比为,
∴
当与在轴同侧时,点的坐标为,
当与在轴异侧时,点的坐标为.
故选.
7.
【答案】
C
【解答】
解:∵
以原点为位似中心,在第一象限内将线段缩小为原来的后得到线段,
∴
端点的横坐标和纵坐标都变为点的横坐标和纵坐标的一半,
又∵
,
∴
端点的坐标为.
故选.
8.
【答案】
D
【解答】
解:∵
把的每一个点横坐标都乘,则对应点的横坐标都互为相反数,纵坐标不变,
∴
与关于轴对称.
故选.
9.
【答案】
C
【解答】
解:∵
与是位似图形,点是位似中心,
、、分别是、、的中点,
∴
两图形的位似之比为,
则与的面积比是.
故选.
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
)
10.
【答案】
【解答】
∵
四边形与四边形位似,
∴
,
∴
,
∴
==,
11.
【答案】
【解答】
解:设点的坐标为,
∵
和是以点为位似中心的位似图形,
∴
,,
解得,,
所以,点的坐标为.
故答案为:.
12.
【答案】
【解答】
解:设较小图形的面积为,则较大图形的面积为,
∵
两个位似图形的对应线段的长度分别为和,
∴
,
解得.
故答案为:.
13.
【答案】
或
【解答】
解:
①当时,
将沿折叠得,
∴
,
∴
,
∴
,
∴
,
∵
,
∴
,
即
,
∴
;
②当
时,如图,
将
沿折叠得
,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
.
综上所述,当
与相似时,的长为或.
故答案为∶或.
14.
【答案】
【解答】
解:∵
与为位似图形,
∴
,
∵
位似比是,
∴
相似比是,
∴
与的面积比为:,
∵
的面积为,
∴
的面积是:.
故答案为:.
15.
【答案】
位似,
【解答】
解:∵
,,
∴
,,
∴
,
∵
的延长线交于于点,
∴
与是位似图形,其中点是位似中心.
故答案为:位似,.
16.
【答案】
,
【解答】
解:∵
,,
∴
,
∴
,,
,,
∴
,,
∴
,
位似比:.
17.
【答案】
【解答】
解:∵
与是以坐标原点为位似中心的位似图形,
且,点,点,
∴
,,
∴
,
故答案为:.
18.
【答案】
【解答】
解:∵
点是与的位似中心,的周长为,
当、、分别是线段、、的中点,则的周长为;
当、、,则的周长为;
…
故当、、,则的周长为:.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:如图:即为所求.
由图可知:,
【解答】
解:如图:即为所求.
由图可知:,
根据原点位似的特点可知.
故答案为:.
20.
【答案】
解:(1)所作图形如图所示:
(2),,
∵
和位似,且位似比为;
∴
,
,
∴
,,
∴
,,
∴
四边形的周长
.
【解答】
解:(1)所作图形如图所示:
(2),,
∵
和位似,且位似比为;
∴
,
,
∴
,,
∴
,,
∴
四边形的周长
.
21.
【答案】
解:
如图?
如图所示,与是关于为位似中心的位似图形.
【解答】
解:
如图?
如图所示,与是关于为位似中心的位似图形.
22.
【答案】
解:如图所示.
四边形.
【解答】
解:如图所示.
四边形.
在中,
∵
,
;
∴
变化后的对应点的坐标为.
故答案为:.
23.
【答案】
解:如图,点即为所求,点的坐标为.
因为,
所以与的位似比为.
如图,为所求,
的坐标为.
【解答】
解:如图,点即为所求,点的坐标为.
因为,
所以与的位似比为.
如图,为所求,
的坐标为.
24.
【答案】
【解答】
此题暂无解答
25.
【答案】
解:如图,连接并延长,交的延长线于点,点即为所求.
则点的坐标为,
与的相似比为.
如图,为所求,
的坐标为.
【解答】
解:如图,连接并延长,交的延长线于点,点即为所求.
则点的坐标为,
与的相似比为.
如图,为所求,
的坐标为.
相似三角形
(满分120分;时间:120分钟)
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如图,下列条件不能判定的是(?
?
?
?
)
A.
B.
C.
D.
?2.
如图,中,点在线段上,且,则下列结论一定正确的是(
)
A.
B.
C.
D.
?3.
如图,已知直线,直线、与直线、、分别交于点、、、、、,=,=,=,则=(
)
A.
B.
C.
D.
?
4.
两个相似三角形的对应边分别是和,它们的周长相差,则这两个三角形的周长分别是?
?
?
?
A.,
B.,
C.,
D.,
?5.
如图,是的边上一点,那么下面四个命题中错误的是(
)
A.如果,则
B.如果,则
C.如果,则
D.如果,则
?
6.
如图,在中,,于,,,则为(
)
A.
B.
C.
D.
?
7.
如图,补充下列一个条件,不能使的是(
)
A.
B.
C.
D.
?
8.
如图,点、分别在的边、上,下列各比例式不一定能推得的是(
)
A.
B.
C.
D.
?
9.
如图,在中,,,平分,,那么在下列三角形中,与相似的三角形是(?
?
?
?
)
A.
B.
C.
D.
?
10.
如图,在中,在边上,,是的中点,连接并延长交于,则的值为?
?
?
?
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
11.
已知,与的相似比为,则与对应边上的高之比为________.
?
12.
如图,,若,,,则的长为________.
?13.
如图,,゜,,.当________,________时,.
?
14.
如图,在中,点在上,请你再添加一个适当的条件:________,使.(注:不添加任何的数字、字母或辅助线)
?
15.
在阳光下,身高的小林在地面上的影长为,在同一时刻,测得学校的旗杆在地面上的影长为,则旗杆的高度为________.
?
16.
如图,中,点、分别在边、上,,若,,,则的长是________.
?
17.
如图,点在的边上,请你添加一个条件,使得,这个条件可以是________.
18.
如图,某测量工作人员与标杆顶端、电视塔顶端在同一直线上,已知此人眼睛距地面米,标杆为米,且米,米,则电视塔的高________.
三、
解答题
(本题共计
7
小题
,共计60分
,
)
?
19.
如图,点为边上一点,请用尺规作图在边上找一点,使得=(保留作图痕迹,不写作法),并说明理由.
?
20.
如图,在方格纸中,以格点连线为边的三角形叫格点三角形,就是格点三角形,请在此方格纸上另画一个与相似的格点三角形,并写出它与的相似比.
?21.
如图,在中,、、分别是、上的点,且,,,,求和的长.
?
22.
如图,在正方形中,点在上,,点在上,试给出点满足什么条件时,与相似.
?
23.
已知:如图中,,.
求证:;
若,,,求的长.
?
24.
一位同学想利用有关知识测旗杆的高度,他在某一时刻测得高为的小木棒的影长为,但当他马上测量旗杆的影长时,因旗杆靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影子,又测地面部分的影长,你能根据上述数据帮他测出旗杆的高度吗?
?
25.
中,,,为上的动点,小慧拿含角的透明三角板,使角的顶点落在点,三角板可绕点旋转.
(1)如图,当三角板的两边分别交、于点、时.求证:;
(2)将三角板绕点旋转到图情形时,三角板的两边分别交的延长线、边于点、.与还相似吗?(只需写出结论)
(3)在(2)的条件下,连结,与是否相似?若不相似,则动点运动到什么位置时,与相似?说明理由.
参考答案
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
D
【解答】
解:,∵
,,∴
,故此选项不合题意;
,∵
,,∴
,故此选项不合题意;
,∵
,∴
,,,故此选项不合题意;
,∵
,∴
,不能判定,故此选项符合题意.
故选.
2.
【答案】
C
【解答】
解:∵
,
而,
∴
,
∴
,
∴
.
故选.
3.
【答案】
B
【解答】
∵
,
∴
,
∵
=,=,=,
∴
,
解得:,
∴
==.
4.
【答案】
A
【解答】
解:根据题意两个三角形的相似比是,周长比就是,
大小周长相差份,所以每份的周长是,
所以两个三角形的周长分别为,.
故选.
5.
【答案】
D
【解答】
解:中,为公共角,所以正确;
中,为公共角,所以也正确;
中对应边成比例,对应角相等,也正确;
中对应边成比例,但夹角不相等,所以错误
故选
6.
【答案】
B
【解答】
解:由射影定理得,
,
∴
.
故选:.
7.
【答案】
D
【解答】
解:∵
,,
∴
,
∴
选项不符合;
∵
,,
∴
,
∴
选项不符合;
∵
,,
∴
,
∴
选项不符合;
虽然,但,
∴
与不相似,
∴
选项符合.
故选:.
8.
【答案】
B
【解答】
∵
,
∴
,
∵
,
∴
,
∵
,
∴
,
9.
【答案】
C
【解答】
解:∵
,,
∴
,
又∵
是的平分线,
∴
,
∵
,
∴
,
即,,
∴
.
故选.
10.
【答案】
B
【解答】
解:如图,过作,交于,
∵
是的中点,
∴
是的中点.
又,
∴
,
∴
,,
∴
,
设,,又,
∴
,,
∵
,
∴
,,
∴
,,
∴
.
故选.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
【解答】
解:∵
,与的相似比为,
∴
与对应边上的高之比是,
故答案为:.
12.
【答案】
【解答】
解:∵
,
∴
,
∴
,
∵
,,,
∴
,
∴
,
解得:.
故答案为:.
13.
【答案】
,
【解答】
解:当,时,
∵
,゜,,,
∴
,,
∴
.
故答案为,.
14.
【答案】
(答案不唯一)
【解答】
解:要使,可以添加条件.
∵
,,
∴
.
故答案为:(答案不唯一).
15.
【答案】
【解答】
解:设旗杆的高度为.
根据在同一时刻身高与影长成比例可得:,
解得:.
故答案为:.
16.
【答案】
【解答】
∵
,
∴
,
∵
,,,
∴
,
解得:,
∴
.
17.
【答案】
【解答】
在与中,为两三角形的公共角,只需再有一对应角相等即可,即,
18.
【答案】
【解答】
解:过点作,交于,交于.
由题意可得:,
∴
即,
解得:.
∴
(米).
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
【解答】
∵
=,
∴
,
∵
=,
∴
.
点
20.
【答案】
解:图形如图:相似比为.(注:答案不唯一,答对即可)
【解答】
解:图形如图:相似比为.(注:答案不唯一,答对即可)
21.
【答案】
解:∵
,
∴
,即,
∴
,
∴
,
∵
,
∴
,即,
∴
,
∴
.
【解答】
解:∵
,
∴
,即,
∴
,
∴
,
∵
,
∴
,即,
∴
,
∴
.
22.
【答案】
解:设正方形的边长为,则,
∵
,
∴
当时,,即,解得,解得;
或当时,,即,整理为,解得,
∴
当点满足或时,与相似.
【解答】
解:设正方形的边长为,则,
∵
,
∴
当时,,即,解得,解得;
或当时,,即,整理为,解得,
∴
当点满足或时,与相似.
23.
【答案】
证明:∵
,
∴
,
∵
,,,
∴
,
∴
;
解:由知,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
【解答】
证明:∵
,
∴
,
∵
,,,
∴
,
∴
;
解:由知,
∴
,
∵
,
∴
,
∵
,
∴
,
∴
.
24.
【答案】
能.旗杆的高度为.
【解答】
解:∵
高为的小木棒的影长为,
∴
实际高度和影长之比为,即,
∴
落在墙上的,如果投射到地面上应该为米,即旗杆的实际影长为米,
∴
,解得,
25.
【答案】
(1)证明:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(2)解:;
理由:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(3)解:动点运动到中点位置时,与相似,
证明:同(1),可证,
得?,
而,
因此?.
又因为,
所以(两边对应成比例且夹角相等的两个三角形相似).
【解答】
(1)证明:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(2)解:;
理由:∵
在中,,,
∴
.
∵
,
∴
,
∵
,
又∵
,
∴
,
∴
,
又∵
,
∴
(两角对应相等的两个三角形相似).
(3)解:动点运动到中点位置时,与相似,
证明:同(1),可证,
得?,
而,
因此?.
又因为,
所以(两边对应成比例且夹角相等的两个三角形相似).
27.3
位似
(满分120分;时间:120分钟)
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
?1.
在平面直角坐标系中,,,,以原点为位似中心,将扩大到原来的倍,若点的对应点坐标为,则点的对应点的坐标为(?
?
?
?
)
A.
B.
C.
D.
?
2.
若一个多边形放大后与原多边形位似,且面积放大为原来的倍,则周长放大为原来的(
)
A.倍
B.倍
C.倍
D.倍
?
3.
在平面直角坐标系中,点,以原点为位似中心,在第一象限内把线段缩小为原来的得到线段,则点的坐标为(?
?
?
?
)
A.
B.
C.
D.
?
4.
在平面直角坐标系中,点
,将以原点为位似中心,相似比为,进行位似变换,则点的对应点的坐标是(?
?
?
?
)
A.
或
B.或
C.或
D.
或
?
5.
如图,四边形与四边形相似,位似中心是点,若=,则的值是(
)
A.
B.
C.
D.
?
6.
在平面直角坐标系中,??的三个顶点的坐标分别为??,?,以原点为位似中心,把这个三角形缩小为原来的??,得到??,则点的对应点的坐标是?
?
?
?
A.
B.
C.或
D.或
?
7.
在平面直角坐标系中,线段两个端点的坐标分别为,,若以原点为位似中心,在第一象限内将线段缩短为原来的后得到线段,则点的对应点的坐标为(
)
A.
B.
C.
D.
?
8.
把的每一个点横坐标都乘,得到,这一变换是(
)
A.位似变换
B.旋转变换
C.中心对称变换
D.轴对称变换
?
9.
如图,与是位似图形,点是位似中心,、、分别是、、的中点,则与的面积比是?
?
?
?
A.
B.
C.
D.
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
,
)
10.
四边形与四边形位似,点为位似中心.若=,则=________.
?
11.
如图,和是以点为位似中心的位似图形,已知,,,则点的对应点的坐标是________.
12.
如果两个位似图形的对应线段的长度分别为和,且面积之和为,则较小的图形的面积为________.
?
13.
如图,在
?,点、分别是,的中点,点是上一点,将沿折叠得,,交于点,当,
相似时,的长为________.
14.
?如图,与为位似图形,点是它们的位似中心,位似比是,且的面积为,那么的面积是________.
15.
已知:如图,,,的延长线交于于点,与是________图形,其中________点是位似中心.
?
16.
已知:如图,,且,则与________是位似图形,位似比为________.
?
17.
如图,已知与是以坐标原点为位似中心的位似图形,且,若点,点,则________.
?
18.
如图,点是与的位似中心,的周长为.若、、分别是线段、、的中点,则的周长为;若、、,则的周长为;…若、、,则的周长为________.(用正整数表示)
三、
解答题
(本题共计
7
小题
,共计66分
,
)
?
19.
如图,已知是坐标原点,,的坐标分别为,.
在轴的左侧以为位似中心作的位似三角形(要求:新图与原图的相似比为
;
分别写出,的对应点,的坐标;
若线段上有一点,则点在上的对应点的坐标为________.
?
20.
如图,在网格图中,每个小正方形边长均为,点和、、三点均为格点.
(1)以为位似中心,在网格图中作,使和位似,且位似比为;
(2)连接(1)中的,求四边形的周长.(结果保留根号)
?
21.
如图,在平面直角坐标系中,、.
画出向左平移个单位长度,再向上平移个单位长度后的;
以原点为位似中心,在轴的右侧画出
的一个位似,使它与的相似比为;
判断与
是否关于某一点为位似中心的位似图形?若是,请在图中标出位似中心,并写出点的坐标.
?
22.
如图,在正方形网格中,四边形的顶点坐标分别为,,,.
以点为位似中心,在位似中心的同侧将四边形放大为原来的倍,放大后点,,的对应点分别为,,画出四边形;
求出四边形的面积.
在中,若为线段上任一点,则变化后点的对应点的坐标为(________).
?
23.
在如图所示的方格中,每个小正方形的边长均为,与是关于点为位似中心的位似图形.
在图中标出位似中心的位置,并写出点的坐标及与的位似比;
以原点为位似中心,在轴的右侧画出的另一个位似,使它与的位似比为,并写出点的对应点的坐标;
?
24.
如图中的小方格都是边长为的正方形,与是关于点为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)画出位似中心点;
(2)求出与的位似比;
(3)以点为位似中心,在所给的网格图的右边再画一个,使它与的位似比等于.
?25.
在如图所示的方格中,的顶点坐标分别为,,,与是关于点为位似中心的位似图形.
在图中标出位似中心的位置,并写出点的坐标及与的相似比;
以原点为位似中心,在轴的左侧画出的另一个位似,使它与的位似比为,并写出点的对应点的坐标;
参考答案
一、
选择题
(本题共计
9
小题
,每题
3
分
,共计27分
)
1.
【答案】
B
【解答】
解:∵
以原点为位似中心,将放大为原来的倍,
点的对应点是,
则点的对应点为.
故选.
2.
【答案】
C
【解答】
解:根据题意,扩大后的多边形与原来的多边形的相似比为,
∴
它们的周长的比为,
∴
周长扩大为原来的倍.
故选:.
3.
【答案】
A
【解答】
解:在平面直角坐标系中,点,以原点为位似中心,
在第一象限内把线段缩小为原来的得到线段,
则点的对应点的坐标为,
即点坐标为.
故选.
4.
【答案】
B
【解答】
解:的一个顶点的坐标是,
以原点为位似中心相似比为,将缩小得到它的位似图形,
∴
点的坐标是:?,,
即或?.
故选
5.
【答案】
B
【解答】
∵
四边形与四边形相似,位似中心是点,=,
∴
四边形与四边形的相似比为:,
∴
=.
6.
【答案】
C
【解答】
解:∵
点,且相似比为,
∴
当与在轴同侧时,点的坐标为,
当与在轴异侧时,点的坐标为.
故选.
7.
【答案】
C
【解答】
解:∵
以原点为位似中心,在第一象限内将线段缩小为原来的后得到线段,
∴
端点的横坐标和纵坐标都变为点的横坐标和纵坐标的一半,
又∵
,
∴
端点的坐标为.
故选.
8.
【答案】
D
【解答】
解:∵
把的每一个点横坐标都乘,则对应点的横坐标都互为相反数,纵坐标不变,
∴
与关于轴对称.
故选.
9.
【答案】
C
【解答】
解:∵
与是位似图形,点是位似中心,
、、分别是、、的中点,
∴
两图形的位似之比为,
则与的面积比是.
故选.
二、
填空题
(本题共计
9
小题
,每题
3
分
,共计27分
)
10.
【答案】
【解答】
∵
四边形与四边形位似,
∴
,
∴
,
∴
==,
11.
【答案】
【解答】
解:设点的坐标为,
∵
和是以点为位似中心的位似图形,
∴
,,
解得,,
所以,点的坐标为.
故答案为:.
12.
【答案】
【解答】
解:设较小图形的面积为,则较大图形的面积为,
∵
两个位似图形的对应线段的长度分别为和,
∴
,
解得.
故答案为:.
13.
【答案】
或
【解答】
解:
①当时,
将沿折叠得,
∴
,
∴
,
∴
,
∴
,
∵
,
∴
,
即
,
∴
;
②当
时,如图,
将
沿折叠得
,
∴
,
∴
,
∵
,
∴
,
∴
,
∴
.
综上所述,当
与相似时,的长为或.
故答案为∶或.
14.
【答案】
【解答】
解:∵
与为位似图形,
∴
,
∵
位似比是,
∴
相似比是,
∴
与的面积比为:,
∵
的面积为,
∴
的面积是:.
故答案为:.
15.
【答案】
位似,
【解答】
解:∵
,,
∴
,,
∴
,
∵
的延长线交于于点,
∴
与是位似图形,其中点是位似中心.
故答案为:位似,.
16.
【答案】
,
【解答】
解:∵
,,
∴
,
∴
,,
,,
∴
,,
∴
,
位似比:.
17.
【答案】
【解答】
解:∵
与是以坐标原点为位似中心的位似图形,
且,点,点,
∴
,,
∴
,
故答案为:.
18.
【答案】
【解答】
解:∵
点是与的位似中心,的周长为,
当、、分别是线段、、的中点,则的周长为;
当、、,则的周长为;
…
故当、、,则的周长为:.
故答案为:.
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:如图:即为所求.
由图可知:,
【解答】
解:如图:即为所求.
由图可知:,
根据原点位似的特点可知.
故答案为:.
20.
【答案】
解:(1)所作图形如图所示:
(2),,
∵
和位似,且位似比为;
∴
,
,
∴
,,
∴
,,
∴
四边形的周长
.
【解答】
解:(1)所作图形如图所示:
(2),,
∵
和位似,且位似比为;
∴
,
,
∴
,,
∴
,,
∴
四边形的周长
.
21.
【答案】
解:
如图?
如图所示,与是关于为位似中心的位似图形.
【解答】
解:
如图?
如图所示,与是关于为位似中心的位似图形.
22.
【答案】
解:如图所示.
四边形.
【解答】
解:如图所示.
四边形.
在中,
∵
,
;
∴
变化后的对应点的坐标为.
故答案为:.
23.
【答案】
解:如图,点即为所求,点的坐标为.
因为,
所以与的位似比为.
如图,为所求,
的坐标为.
【解答】
解:如图,点即为所求,点的坐标为.
因为,
所以与的位似比为.
如图,为所求,
的坐标为.
24.
【答案】
【解答】
此题暂无解答
25.
【答案】
解:如图,连接并延长,交的延长线于点,点即为所求.
则点的坐标为,
与的相似比为.
如图,为所求,
的坐标为.
【解答】
解:如图,连接并延长,交的延长线于点,点即为所求.
则点的坐标为,
与的相似比为.
如图,为所求,
的坐标为.
