人教版数学8年级上册12.2三角形全等的判定测试题(二)(Word版 含答案)
文档属性
| 名称 | 人教版数学8年级上册12.2三角形全等的判定测试题(二)(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 74.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览


文档简介
12.2三角形全等的判定测试题(二)及答案
一.
选择题:
1.
下列各图中,一定全等的是(
)
A.
各有一个角是的两个等腰三角形
B.
两个等边三角形
C.
各有一个角是,腰长都是3cm的两个等腰三角形
D.
腰和顶角对应相等的两个等腰三角形
2.
在和中,,,若证还要从下列条件中补选一个,错误的选法是(
)
A.
B.
C.
D.
3.
如图AB=AC,BE、CF分别为AC、AB边上的高,图中与相等的角有(
)
A.
1个
B.
2个
C.
3个
D.
0个
4.
如图,∠1=∠2,∠3=∠4,则图中全等的三角形的对数是(
)
A.
3
B.
4
C.
5
D.
6
5.
如图在中,,AC=BC,AD平分交BC于D,DE⊥AB于E,若AB=6cm,则的周长是(
)
A.
6cm
B.
7cm
C.
8cm
D.
9
cm
6.
在和中,,且,,则这两个三角形(
)
A.
不一定全等
B.
不全等
C.
根据“SAS”全等
D.
根据“ASA”全等
7.
如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是(
)
A.
∠DAE=∠CBE
B.
CE=DE
C.
不全等于
D.
是等腰三角形
?
二.
填空题:
1.
已知,有,,则
。
2.
如图在中,,且则
=
。
3.
已知,BC=EF=6cm,的面积为,则EF边上的高的长是
。
4.
如图AD=AB,,,则
。
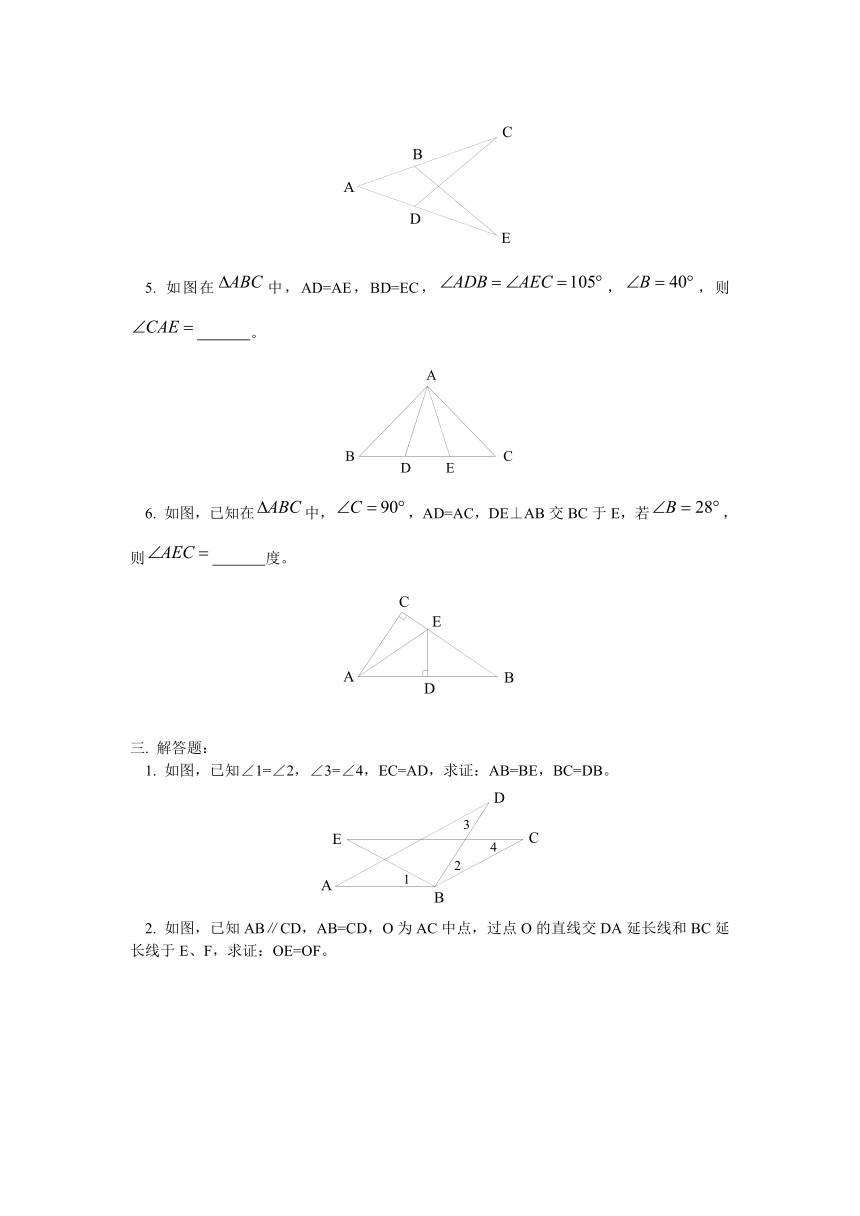
5.
如图在中,AD=AE,BD=EC,,,则
。
6.
如图,已知在中,,AD=AC,DE⊥AB交BC于E,若,则
度。
?
三.
解答题:
1.
如图,已知∠1=∠2,∠3=∠4,EC=AD,求证:AB=BE,BC=DB。
2.
如图,已知AB∥CD,AB=CD,O为AC中点,过点O的直线交DA延长线和BC延长线于E、F,求证:OE=OF。
3.
如图,已知AB=AD,AC平分∠DAB,求证:。
4.
如图(1)在四边形ABCD中,AD∥BC,,AB=DC,AE=DF。
(1)求证:BF=CE。
(2)当E、F相向运动,形成图(2)时,BF和CE还相等吗?请证明你的结论。
(1)
(2)
?
答案
一.
1.
D
2.
C
3.
A
4.
D
5.
A
6.
A
7.
C
?
二.
1.
2.
3.
6cm
4.
5.
6.
59
?
三.
1.
证明:∵
∠1=∠2
∴
∴
在与中,
∴
(AAS)
∴
AB=BE,BC=DB(全等三角形对应边相等)
2.
证明:∵
AB∥CD
∴
∠1=∠2
∴
O为AC中点
∴
AO=CO
在与中,
∴
(SAS)
∴
(全等三角形对应角相等)
∴
AD∥BC(内错角相等两直线平行)
∴
∠E=∠F
在与中,
∴
(AAS)
∴
EO=OF(全等三角形对应边相等)
3.
证明:∵
AC平分∠DAB
∴
∠1=∠2
在与中,
∴
(SAS)
∴
∠3=∠4
DC=BC(全等三角形对应边、对应角分别相等)
在与中,
∴
∴
(全等三角形对应角相等)
4.
证明:
(1)∵
AD∥BC
∠1+∠ABC=180°
∠2+∠DCB=180°
∵
∴
∠1=∠2
∵
AE=DF
∴
AD+DF=AD+AE
∴
AF=ED
在与中,
∴
(SAS)
∴
BF=CE(全等三角形对应边相等)
(2)答:EF和CE相等,此时A与E重合,D与F重合。
证明:∵
AD∥BC
∴
∵
∴
在与中,
∴
(SAS)
∴
BD=AC
即BF=CE
?
一.
选择题:
1.
下列各图中,一定全等的是(
)
A.
各有一个角是的两个等腰三角形
B.
两个等边三角形
C.
各有一个角是,腰长都是3cm的两个等腰三角形
D.
腰和顶角对应相等的两个等腰三角形
2.
在和中,,,若证还要从下列条件中补选一个,错误的选法是(
)
A.
B.
C.
D.
3.
如图AB=AC,BE、CF分别为AC、AB边上的高,图中与相等的角有(
)
A.
1个
B.
2个
C.
3个
D.
0个
4.
如图,∠1=∠2,∠3=∠4,则图中全等的三角形的对数是(
)
A.
3
B.
4
C.
5
D.
6
5.
如图在中,,AC=BC,AD平分交BC于D,DE⊥AB于E,若AB=6cm,则的周长是(
)
A.
6cm
B.
7cm
C.
8cm
D.
9
cm
6.
在和中,,且,,则这两个三角形(
)
A.
不一定全等
B.
不全等
C.
根据“SAS”全等
D.
根据“ASA”全等
7.
如图,∠1=∠2,∠C=∠D,AC、BD交于E点,下列结论中不正确的是(
)
A.
∠DAE=∠CBE
B.
CE=DE
C.
不全等于
D.
是等腰三角形
?
二.
填空题:
1.
已知,有,,则
。
2.
如图在中,,且则
=
。
3.
已知,BC=EF=6cm,的面积为,则EF边上的高的长是
。
4.
如图AD=AB,,,则
。
5.
如图在中,AD=AE,BD=EC,,,则
。
6.
如图,已知在中,,AD=AC,DE⊥AB交BC于E,若,则
度。
?
三.
解答题:
1.
如图,已知∠1=∠2,∠3=∠4,EC=AD,求证:AB=BE,BC=DB。
2.
如图,已知AB∥CD,AB=CD,O为AC中点,过点O的直线交DA延长线和BC延长线于E、F,求证:OE=OF。
3.
如图,已知AB=AD,AC平分∠DAB,求证:。
4.
如图(1)在四边形ABCD中,AD∥BC,,AB=DC,AE=DF。
(1)求证:BF=CE。
(2)当E、F相向运动,形成图(2)时,BF和CE还相等吗?请证明你的结论。
(1)
(2)
?
答案
一.
1.
D
2.
C
3.
A
4.
D
5.
A
6.
A
7.
C
?
二.
1.
2.
3.
6cm
4.
5.
6.
59
?
三.
1.
证明:∵
∠1=∠2
∴
∴
在与中,
∴
(AAS)
∴
AB=BE,BC=DB(全等三角形对应边相等)
2.
证明:∵
AB∥CD
∴
∠1=∠2
∴
O为AC中点
∴
AO=CO
在与中,
∴
(SAS)
∴
(全等三角形对应角相等)
∴
AD∥BC(内错角相等两直线平行)
∴
∠E=∠F
在与中,
∴
(AAS)
∴
EO=OF(全等三角形对应边相等)
3.
证明:∵
AC平分∠DAB
∴
∠1=∠2
在与中,
∴
(SAS)
∴
∠3=∠4
DC=BC(全等三角形对应边、对应角分别相等)
在与中,
∴
∴
(全等三角形对应角相等)
4.
证明:
(1)∵
AD∥BC
∠1+∠ABC=180°
∠2+∠DCB=180°
∵
∴
∠1=∠2
∵
AE=DF
∴
AD+DF=AD+AE
∴
AF=ED
在与中,
∴
(SAS)
∴
BF=CE(全等三角形对应边相等)
(2)答:EF和CE相等,此时A与E重合,D与F重合。
证明:∵
AD∥BC
∴
∵
∴
在与中,
∴
(SAS)
∴
BD=AC
即BF=CE
?
