鲁教版(五四制)八年级数学上册 第四章 图形的平移与旋转 同步练习(word版无答案)
文档属性
| 名称 | 鲁教版(五四制)八年级数学上册 第四章 图形的平移与旋转 同步练习(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 260.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览


文档简介
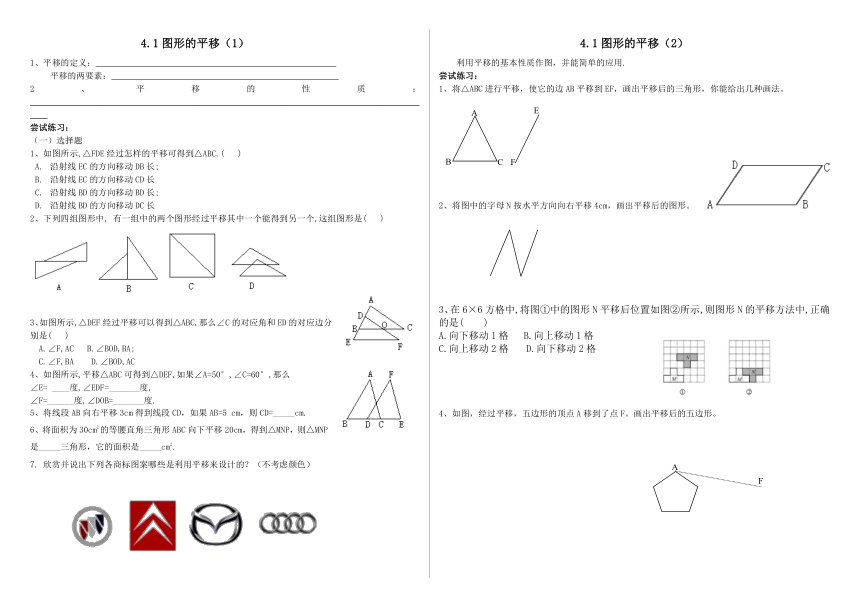
4.1图形的平移(1)
1、平移的定义:
平移的两要素:
2、平移的性质:
_____________________________________________________________________________________________
尝试练习:
(一)选择题
1、如图所示,△FDE经过怎样的平移可得到△ABC.(
)
沿射线EC的方向移动DB长;
沿射线EC的方向移动CD长
沿射线BD的方向移动BD长;
沿射线BD的方向移动DC长
2、下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是(
)
3、如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是(
)
A.∠F,AC
B.∠BOD,BA;
C.∠F,BA
D.∠BOD,AC
4、如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么
∠E=____度,∠EDF=_______度,
∠F=______度,∠DOB=_______度.
5、将线段AB向右平移3cm得到线段CD,如果AB=5
cm,则CD=_____cm.
6、将面积为30cm2的等腰直角三角形ABC向下平移20cm,得到△MNP,则△MNP是_____三角形,它的面积是_____cm2.
7.
欣赏并说出下列各商标图案哪些是利用平移来设计的?(不考虑颜色)
4.1图形的平移(2)
利用平移的基本性质作图,并能简单的应用.
尝试练习:
1、将△ABC进行平移,使它的边AB平移到EF,画出平移后的三角形,你能给出几种画法。
2、将图中的字母N按水平方向向右平移4cm,画出平移后的图形。
3、在6×6方格中,将图①中的图形N平移后位置如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格
B.向上移动1格
C.向上移动2格
D.向下移动2格
4、如图,经过平移,五边形的顶点A移到了点F。画出平移后的五边形。
4.1图形的平移(3)
把直角坐标系中的一个图形按下列要求平移,那么图形中的一点的坐标是(x,y)将如何变化?(a>0,b>0)
(1)(x,y)
((
,
)
(2)(x,y)
(
,
)
(3)(x,y)
((
,
)
(4)(x,y)
((
,
)
尝试练习:
1.将点A(﹣2,﹣3)向右平移3个单位长度得到点B,则点B所处的象限是( )
A
第一象限
B
第二象限
C
第三象限
D
第四象限
2.在平面直角坐标系中,将点P(﹣2,3)向下平移4个单位得到点P′,则点P′所在象限为( )
A
第一象限
B
第二象限
C
第三象限
D
第四象限
3.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )
A
(﹣3,2)
B
(﹣1,2)
C
(1,2)
D
(1,﹣2)
4、如图,点A,B的坐标分别为A(-1,2),B
(-3,-2),
(1)将线段AB沿x轴方向向右平移4个单位长度,得到线段CD,则点C的坐标为(
,
),点D的坐标为(
,
),并画出线段CD。
(2)将线段AB沿x轴方向向下平移2个单位长度,得到线段EF,则点E的坐标为(
,
),点F的坐标为(
,
),并画出线段EF。
4.2
图形的旋转(1)
(一)旋转的概念
在平面内,将一个图形绕一个
按
转动一个角度,图形的这种变化称为
,这个定点称为
,转动的角度称为
。
如右图,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,则点A的对应点为
,B的对应点为
,C的对应点为
,AB的对应线段为
,BC的对应线段为
,AC的对应线段为
,旋转中心是
,旋转角是
。△ABC与△DEF的关系是
。
(二)旋转的基本性质
一般地,我们可以得到:一个图形和它经过旋转所得到的图形中,
(1)
到
的距离相等;
(2)任意一组
与
的连线所成的角都等于
;
(3)
相等,
相等。
尝试练习:
1、如图,四边形ABCD是正方形,E是BC边上的一点,延长BA至F,使AF=CE,连接DE,DF。
(1)△DAF可以看做是△DCE通过旋转得到的吗?如果是,旋转中心是哪一点?旋转角是多少度?
(2)指出图中相等的线段、相等的角。
2、如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=
.
3、如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为
。
4.2
图形的旋转(2)
能够按要求做出简单平面图形旋转后的图形。
尝试练习:
1、线段AB绕点O旋转后,点A旋转到点A’。画出线段AB绕点O旋转后所得到的线段。
2、画出△ABC绕边AB的中点O旋转180度后的图形。
3、四边形ABCD绕点D旋转,边AD旋转到了ED的位置,画出旋转后的四边形。
4、在直角坐标系中,△ABC的顶点坐标分别为A(-1,0),B(0,-2),C(-3,-3),将△ABC绕原点O按逆时针方向旋转90度。
(1)写出旋转后三角形各顶点的坐标;
(2)画出旋转后的图形。
4.3
中心对称
1.
定义:
中心对称:_____________________________________________________________________
中心对称图形:_________________________________________________________________
2.
如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成________________.
3.中心对称的性质:
成中心对称的两个图形中,对应点所连接线段经过______,且被对称中心_______
尝试练习:
1.中心对称图形的定义:把一个图形绕着 旋转 度后能与自身重合的图形称为中心对称图形,这个中心点叫做 .?
2.把一个图形绕着中心旋转 后能与另一个图形重合则这 个图形关于这个点中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.?
3、下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的为( )
B.
C.
D.
4、在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P'的坐标为( )
A.(3,2) B.(2,-3) C.(-3,-2) D.(3,-2)
5、如图1,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
A.34° B.36° C.38° D.40°
6.
如图8,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是________.
5.画一个与已知四边形ABCD成中心对称的图形.
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心.
4.4 图形变化的简单应用
灵活运用平移、旋转与轴对称的组合进行简单的图案设计。
尝试练习:
1.万花筒是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心( )
(A)顺时针旋转60°得到的
(B)顺时针旋转120°得到的
(C)逆时针旋转60°得到的
(D)逆时针旋转120°得到的
2.如图所示,对该图案的形成过程叙述正确的是( )
(A)它可以看作是一只小狗绕图案的中心位置旋转90°,180°,270°形成
(B)它可以看作是相邻两只小狗绕图案的中心位置旋转180°形成
(C)它可以看作是相邻两只小狗绕图案的恰当的对称轴翻折而成的
(D)它可以看作是左侧、上面的小狗分别向右侧、下方平移得到的
第1题图
第2题图
3.如图,方格纸上的四边形A'B'C'D'是由四边形ABCD经过变换得到的,试说出它的变换过程?
4.推理证明:如图12,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,
∠B=∠D,AB=AD.
(1)求证:△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕着点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
第四章
拓展提高
1.如图,O为原点,点A的坐标为(-1,2),将△ABO绕点O顺时针旋转90°后得到△CEO,则点A的对应点C的坐标为(
)
A.(1,2)
B.(2,1)
C.(-2,1)
D.(-2,-1)
2.一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是__________(把所有你认为正确的序号都写上)。
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变。
3.如图,将△ABC平移到△A’B’C’的位置(点B’在AC边上),若∠B=55°,∠C=100°,则∠AB’A’的度数为___________。
4.如图,在一块长为12cm,宽为6cm的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm),则空白部分表示的草地面积______________。
5.如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E。
(1)如图1,猜想∠QEP=___________;
(2)如图2,图3,若当∠DAC是锐角或钝角时,其他条件不变,猜想∠QEP的度数,选取一种情况加以证明。
1、平移的定义:
平移的两要素:
2、平移的性质:
_____________________________________________________________________________________________
尝试练习:
(一)选择题
1、如图所示,△FDE经过怎样的平移可得到△ABC.(
)
沿射线EC的方向移动DB长;
沿射线EC的方向移动CD长
沿射线BD的方向移动BD长;
沿射线BD的方向移动DC长
2、下列四组图形中,有一组中的两个图形经过平移其中一个能得到另一个,这组图形是(
)
3、如图所示,△DEF经过平移可以得到△ABC,那么∠C的对应角和ED的对应边分别是(
)
A.∠F,AC
B.∠BOD,BA;
C.∠F,BA
D.∠BOD,AC
4、如图所示,平移△ABC可得到△DEF,如果∠A=50°,∠C=60°,那么
∠E=____度,∠EDF=_______度,
∠F=______度,∠DOB=_______度.
5、将线段AB向右平移3cm得到线段CD,如果AB=5
cm,则CD=_____cm.
6、将面积为30cm2的等腰直角三角形ABC向下平移20cm,得到△MNP,则△MNP是_____三角形,它的面积是_____cm2.
7.
欣赏并说出下列各商标图案哪些是利用平移来设计的?(不考虑颜色)
4.1图形的平移(2)
利用平移的基本性质作图,并能简单的应用.
尝试练习:
1、将△ABC进行平移,使它的边AB平移到EF,画出平移后的三角形,你能给出几种画法。
2、将图中的字母N按水平方向向右平移4cm,画出平移后的图形。
3、在6×6方格中,将图①中的图形N平移后位置如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格
B.向上移动1格
C.向上移动2格
D.向下移动2格
4、如图,经过平移,五边形的顶点A移到了点F。画出平移后的五边形。
4.1图形的平移(3)
把直角坐标系中的一个图形按下列要求平移,那么图形中的一点的坐标是(x,y)将如何变化?(a>0,b>0)
(1)(x,y)
((
,
)
(2)(x,y)
(
,
)
(3)(x,y)
((
,
)
(4)(x,y)
((
,
)
尝试练习:
1.将点A(﹣2,﹣3)向右平移3个单位长度得到点B,则点B所处的象限是( )
A
第一象限
B
第二象限
C
第三象限
D
第四象限
2.在平面直角坐标系中,将点P(﹣2,3)向下平移4个单位得到点P′,则点P′所在象限为( )
A
第一象限
B
第二象限
C
第三象限
D
第四象限
3.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )
A
(﹣3,2)
B
(﹣1,2)
C
(1,2)
D
(1,﹣2)
4、如图,点A,B的坐标分别为A(-1,2),B
(-3,-2),
(1)将线段AB沿x轴方向向右平移4个单位长度,得到线段CD,则点C的坐标为(
,
),点D的坐标为(
,
),并画出线段CD。
(2)将线段AB沿x轴方向向下平移2个单位长度,得到线段EF,则点E的坐标为(
,
),点F的坐标为(
,
),并画出线段EF。
4.2
图形的旋转(1)
(一)旋转的概念
在平面内,将一个图形绕一个
按
转动一个角度,图形的这种变化称为
,这个定点称为
,转动的角度称为
。
如右图,△ABC绕点O按顺时针方向旋转一个角度,得到△DEF,则点A的对应点为
,B的对应点为
,C的对应点为
,AB的对应线段为
,BC的对应线段为
,AC的对应线段为
,旋转中心是
,旋转角是
。△ABC与△DEF的关系是
。
(二)旋转的基本性质
一般地,我们可以得到:一个图形和它经过旋转所得到的图形中,
(1)
到
的距离相等;
(2)任意一组
与
的连线所成的角都等于
;
(3)
相等,
相等。
尝试练习:
1、如图,四边形ABCD是正方形,E是BC边上的一点,延长BA至F,使AF=CE,连接DE,DF。
(1)△DAF可以看做是△DCE通过旋转得到的吗?如果是,旋转中心是哪一点?旋转角是多少度?
(2)指出图中相等的线段、相等的角。
2、如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A=
.
3、如图,△ABC中,∠C=67°,将△ABC绕点A顺时针旋转后,得到△AB′C′,且C′在边BC上,则∠B′C′B的度数为
。
4.2
图形的旋转(2)
能够按要求做出简单平面图形旋转后的图形。
尝试练习:
1、线段AB绕点O旋转后,点A旋转到点A’。画出线段AB绕点O旋转后所得到的线段。
2、画出△ABC绕边AB的中点O旋转180度后的图形。
3、四边形ABCD绕点D旋转,边AD旋转到了ED的位置,画出旋转后的四边形。
4、在直角坐标系中,△ABC的顶点坐标分别为A(-1,0),B(0,-2),C(-3,-3),将△ABC绕原点O按逆时针方向旋转90度。
(1)写出旋转后三角形各顶点的坐标;
(2)画出旋转后的图形。
4.3
中心对称
1.
定义:
中心对称:_____________________________________________________________________
中心对称图形:_________________________________________________________________
2.
如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成________________.
3.中心对称的性质:
成中心对称的两个图形中,对应点所连接线段经过______,且被对称中心_______
尝试练习:
1.中心对称图形的定义:把一个图形绕着 旋转 度后能与自身重合的图形称为中心对称图形,这个中心点叫做 .?
2.把一个图形绕着中心旋转 后能与另一个图形重合则这 个图形关于这个点中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.?
3、下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的为( )
B.
C.
D.
4、在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P'的坐标为( )
A.(3,2) B.(2,-3) C.(-3,-2) D.(3,-2)
5、如图1,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数是( )
A.34° B.36° C.38° D.40°
6.
如图8,△ABC的三个顶点都在方格纸的格点上,其中点A的坐标是(-1,0).现将△ABC绕点A顺时针旋转90°,则旋转后点C的坐标是________.
5.画一个与已知四边形ABCD成中心对称的图形.
(1)以顶点A为对称中心;
(2)以BC边的中点为对称中心.
4.4 图形变化的简单应用
灵活运用平移、旋转与轴对称的组合进行简单的图案设计。
尝试练习:
1.万花筒是由三块等宽等长的玻璃片围成的.如图是看到的万花筒的一个图案,图中所有小三角形均是全等的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为中心( )
(A)顺时针旋转60°得到的
(B)顺时针旋转120°得到的
(C)逆时针旋转60°得到的
(D)逆时针旋转120°得到的
2.如图所示,对该图案的形成过程叙述正确的是( )
(A)它可以看作是一只小狗绕图案的中心位置旋转90°,180°,270°形成
(B)它可以看作是相邻两只小狗绕图案的中心位置旋转180°形成
(C)它可以看作是相邻两只小狗绕图案的恰当的对称轴翻折而成的
(D)它可以看作是左侧、上面的小狗分别向右侧、下方平移得到的
第1题图
第2题图
3.如图,方格纸上的四边形A'B'C'D'是由四边形ABCD经过变换得到的,试说出它的变换过程?
4.推理证明:如图12,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,
∠B=∠D,AB=AD.
(1)求证:△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕着点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
第四章
拓展提高
1.如图,O为原点,点A的坐标为(-1,2),将△ABO绕点O顺时针旋转90°后得到△CEO,则点A的对应点C的坐标为(
)
A.(1,2)
B.(2,1)
C.(-2,1)
D.(-2,-1)
2.一个图形无论经过平移变换还是旋转变换,下列结论一定正确的是__________(把所有你认为正确的序号都写上)。
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变。
3.如图,将△ABC平移到△A’B’C’的位置(点B’在AC边上),若∠B=55°,∠C=100°,则∠AB’A’的度数为___________。
4.如图,在一块长为12cm,宽为6cm的矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm),则空白部分表示的草地面积______________。
5.如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E。
(1)如图1,猜想∠QEP=___________;
(2)如图2,图3,若当∠DAC是锐角或钝角时,其他条件不变,猜想∠QEP的度数,选取一种情况加以证明。
