沪科版九年级数学下册24.4直线和圆的位置关系中考题汇编(Word版 含答案)
文档属性
| 名称 | 沪科版九年级数学下册24.4直线和圆的位置关系中考题汇编(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 461.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览

文档简介
沪科版九年级数学下册直线和圆的位置关系中考题汇编2020
12
一、
选择题
1.
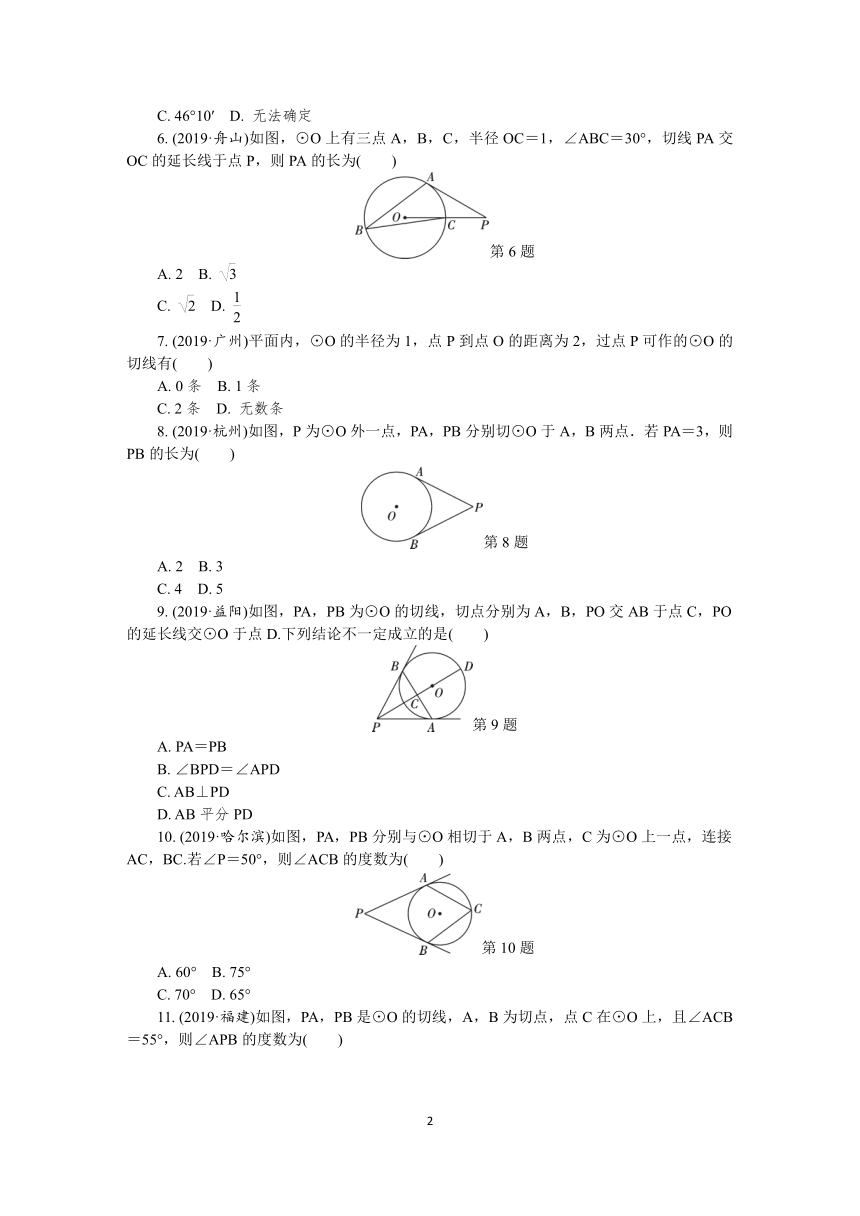
(2019·重庆)如图,AB是⊙O的直径,AC是⊙O的切线,A为切点.若∠C=40°,则∠B的度数为( )
A.
60°
B.
50°
C.
40°
D.
30°
2.
(2019·苏州)如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.
若∠ABO=36°,则∠ADC的度数为( )
A.
54°
B.
36°
C.
32°
D.
27°
3.
(2019·重庆)如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.
若∠C=50°,则∠AOD的度数为( )
A.
40°
B.
50°
C.
80°
D.
100°
4.
(2019·无锡)如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B.若∠P=40°,则∠B的度数为( )
A.
20°
B.
25°
C.
40°
D.
50°
5.
(2018·鄂尔多斯)以O为中心点的量角器与直角三角尺ABC按如图所示的方式摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角尺只有一个公共点P,则∠CBD的度数是( )
A.
45°10′
B.
44°50′
C.
46°10′
D.
无法确定
6.
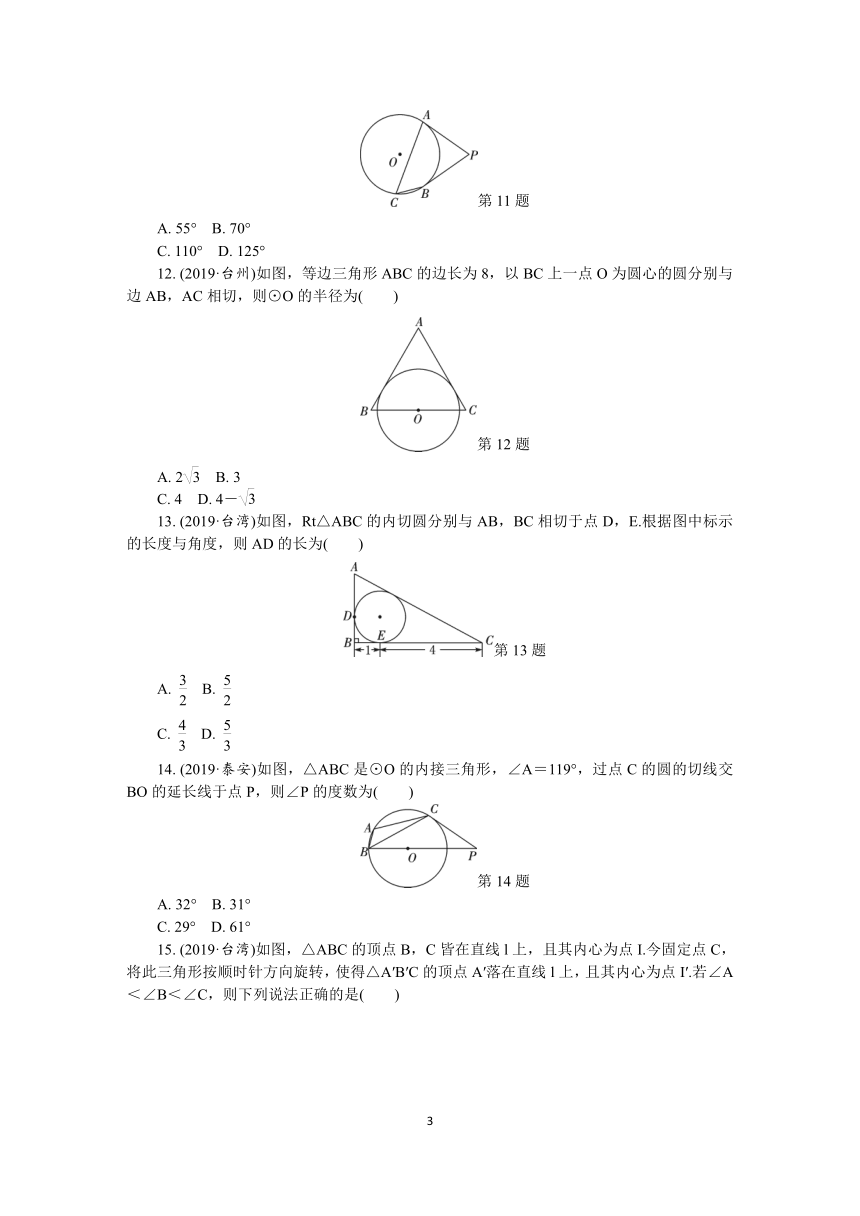
(2019·舟山)如图,⊙O上有三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.
2
B.
C.
D.
7.
(2019·广州)平面内,⊙O的半径为1,点P到点O的距离为2,过点P可作的⊙O的切线有( )
A.
0条
B.
1条
C.
2条
D.
无数条
8.
(2019·杭州)如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB的长为( )
A.
2
B.
3
C.
4
D.
5
9.
(2019·益阳)如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D.下列结论不一定成立的是( )
A.
PA=PB
B.
∠BPD=∠APD
C.
AB⊥PD
D.
AB平分PD
10.
(2019·哈尔滨)如图,PA,PB分别与⊙O相切于A,B两点,C为⊙O上一点,连接AC,BC.若∠P=50°,则∠ACB的度数为( )
A.
60°
B.
75°
C.
70°
D.
65°
11.
(2019·福建)如图,PA,PB是⊙O的切线,A,B为切点,点C在⊙O上,且∠ACB=55°,则∠APB的度数为( )
A.
55°
B.
70°
C.
110°
D.
125°
12.
(2019·台州)如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.
2
B.
3
C.
4
D.
4-
13.
(2019·台湾)如图,Rt△ABC的内切圆分别与AB,BC相切于点D,E.根据图中标示的长度与角度,则AD的长为( )
A.
B.
C.
D.
14.
(2019·泰安)如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO的延长线于点P,则∠P的度数为( )
A.
32°
B.
31°
C.
29°
D.
61°
15.
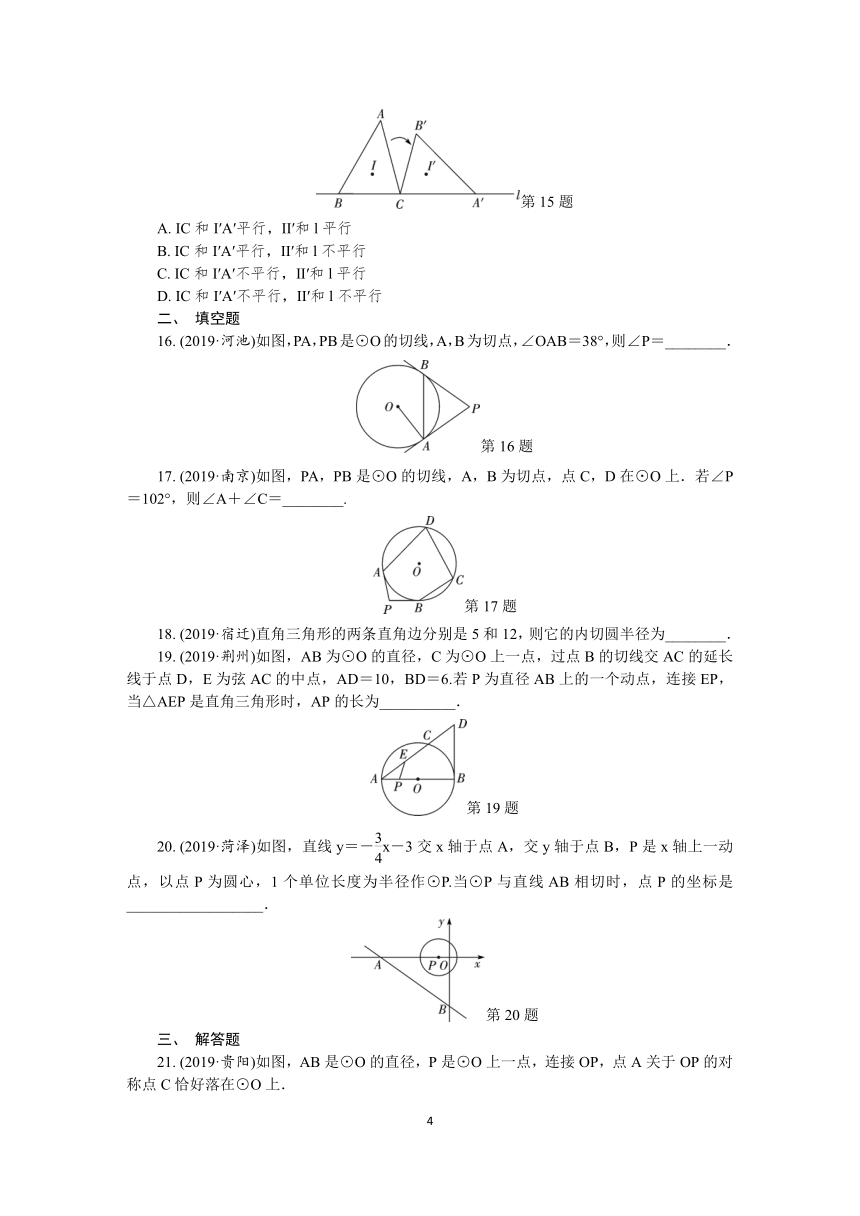
(2019·台湾)如图,△ABC的顶点B,C皆在直线l上,且其内心为点I.今固定点C,将此三角形按顺时针方向旋转,使得△A′B′C的顶点A′落在直线l上,且其内心为点I′.若∠A<∠B<∠C,则下列说法正确的是( )
A.
IC和I′A′平行,II′和l平行
B.
IC和I′A′平行,II′和l不平行
C.
IC和I′A′不平行,II′和l平行
D.
IC和I′A′不平行,II′和l不平行
二、
填空题
16.
(2019·河池)如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=________.
17.
(2019·南京)如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上.若∠P=102°,则∠A+∠C=________.
18.
(2019·宿迁)直角三角形的两条直角边分别是5和12,则它的内切圆半径为________.
19.
(2019·荆州)如图,AB为⊙O的直径,C为⊙O上一点,过点B的切线交AC的延长线于点D,E为弦AC的中点,AD=10,BD=6.若P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为__________.
20.
(2019·菏泽)如图,直线y=-x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,1个单位长度为半径作⊙P.当⊙P与直线AB相切时,点P的坐标是__________________.
三、
解答题
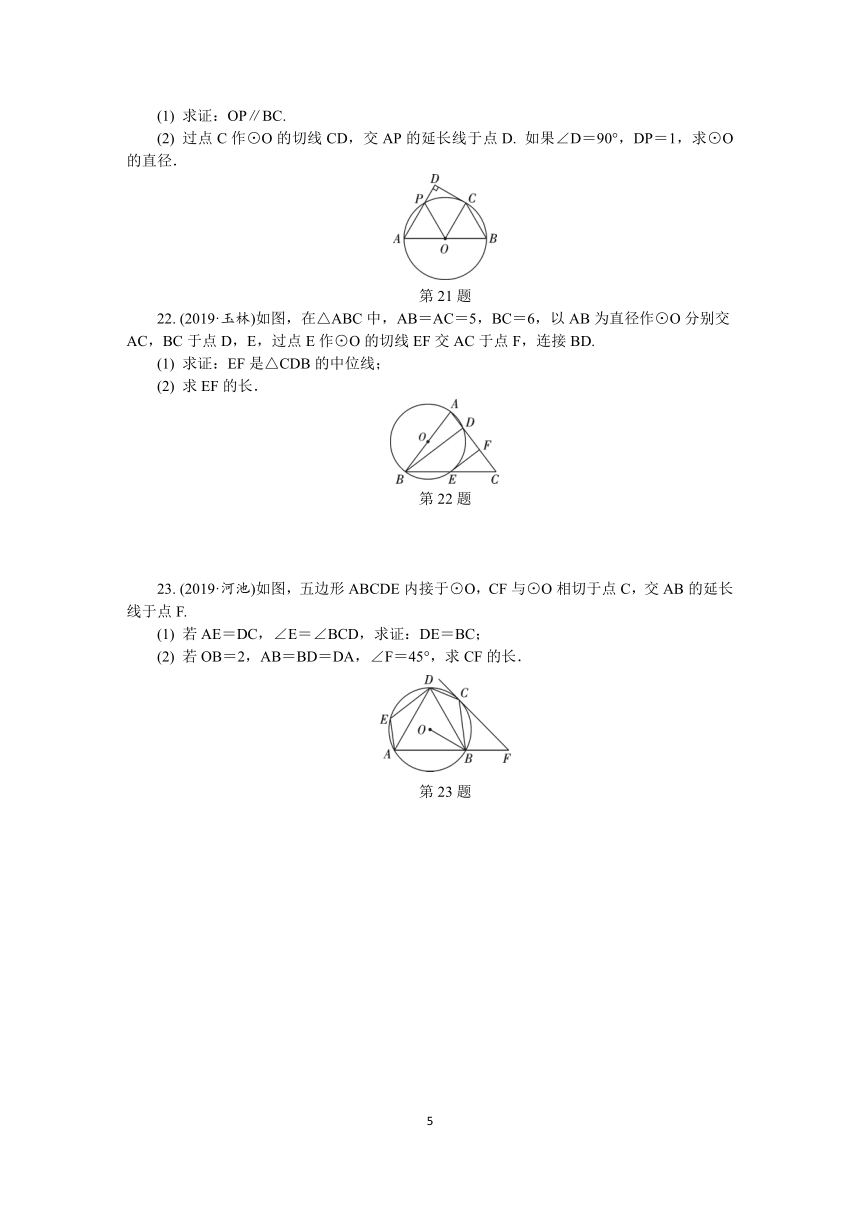
21.
(2019·贵阳)如图,AB是⊙O的直径,P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)
求证:OP∥BC.
(2)
过点C作⊙O的切线CD,交AP的延长线于点D.
如果∠D=90°,DP=1,求⊙O的直径.
第21题
22.
(2019·玉林)如图,在△ABC中,AB=AC=5,BC=6,以AB为直径作⊙O分别交AC,BC于点D,E,过点E作⊙O的切线EF交AC于点F,连接BD.
(1)
求证:EF是△CDB的中位线;
(2)
求EF的长.
第22题
23.
(2019·河池)如图,五边形ABCDE内接于⊙O,CF与⊙O相切于点C,交AB的延长线于点F.
(1)
若AE=DC,∠E=∠BCD,求证:DE=BC;
(2)
若OB=2,AB=BD=DA,∠F=45°,求CF的长.
第23题
24.
(2019·孝感)如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)
求证:DG∥CA;
(2)
求证:AD=ID;
(3)
若DE=4,BE=5,求BI的长.
第24题
25.
(2019·徐州)如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.过点D作直线AC的垂线,垂足为E,连接OD.
(1)
求证:∠A=∠DOB.
(2)
DE与⊙O有怎样的位置关系?请说明理由.
第25题
26.
(2019·江西)如图①,AB为半圆O的直径,AF为半圆O的切线,过半圆O上的点C作CD∥AB交AF于点D,连接BC.
(1)
连接DO,若BC∥OD,求证:CD是半圆O的切线;
(2)
如图②,当线段CD与半圆O交于点E时,连接AE,AC,判断∠AED和∠ACD之间的数量关系,并证明你的结论.
27.
(2019·淮安)如图,AB是⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.
(1)
试判断直线DE与⊙O的位置关系,并说明理由;
(2)
若⊙O的半径为2,∠BAC=60°,求线段EF的长.
第27题
28.
(2019·锦州)如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)
求证:MF是⊙O的切线;
(2)
若CN=3,BN=4,求CM的长.
第28题
29.
(2019·雅安)如图,AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于点E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长,交BA的延长线于点F.
(1)
求证:DC是⊙O的切线;
(2)
若∠ABC=30°,AB=8,求线段CF的长.
第29题
30.
(2019·贺州)如图,BD是⊙O的直径,弦BC与OA相交于点E,AF与⊙O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.
求:
(1)
∠ADB的度数;
(2)
AC的长.
第30题
31.
(2019·大连)如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点A的切线与CD的延长线相交于点P,且∠APC=∠BCP.
(1)
求证:∠BAC=2∠ACD.
(2)
过点D作DE⊥AC,垂足为E.当BC=6,AE=2时,求⊙O的半径.
第31题
参考答案
一、
B
D
C
B
D
B
C
B
D
D
B
A
D
A
C
二、
76°
219°
2
4或2.56
或
三、
(1)
∵
点A关于OP的对称点C恰好落在⊙O上.∴
=.∴
∠AOP=∠COP.∴
∠AOP=∠AOC.又∵
∠ABC=∠AOC,∴
∠AOP=∠ABC.∴
OP∥BC (2)
如图,连接PC.∵
CD为⊙O的切线,∴
OC⊥CD,即∠OCD=90°.又∵
∠D=90°,∴
∠OCD+∠D=180°.∴
OC∥AD.∴
∠APO=∠COP.∵
∠AOP=∠COP,∴
∠APO=∠AOP.∴
OA=AP.∵
OA=OP,∴
OA=AP=OP.∴
△APO为等边三角形.∴
∠AOP=60°.∴
∠COP=∠AOP=60°.∵
OP=OC,∴
△POC为等边三角形.∴
∠PCO=60°,PC=OP.又∵
∠OCD=90°,∴
∠PCD=30°.∵
DP=1,∠D=90°,∴
PC=2DP=2.∴
AB=2OP=2PC=4.∴
⊙O的直径为4
(1)
如图,连接AE,OE.∵
AB为⊙O的直径,∴
∠ADB=∠AEB=90°.∴
BD⊥AC,AE⊥BC.又∵
AB=AC,∴
BE=CE=3.∵
EF是⊙O的切线,∴
OE⊥EF.∵
OA=OB,∴
OE是△ABC的中位线.∴
OE∥AC.∴
OE⊥BD.∴
BD∥EF.∵
BE=CE,∴
易得CF=DF.∴
EF是△CDB的中位线 (2)
∵
∠AEB=90°,∴
AE===4.∵
S△ABC=AC·BD=BC·AE,∴
BD===.∵
EF是△CDB的中位线,∴
EF=BD=
(1)
∵
AE=DC,∴
∠ADE=∠DBC.在△ADE和△DBC中,∴
△ADE≌△DBC.∴
DE=BC (2)
如图,连接CO并延长,交AB于点G,过点O作OH⊥AB于点H.∴
∠OHG=∠OHB=90°.∵
CF与⊙O相切于点C,∴
OC⊥FC,即∠FCG=90°.∵
∠F=45°,∴
易得△CFG,△OGH是等腰直角三角形.∴
CF=CG,OH=HG.∵
AB=BD=DA,∴
△ABD是等边三角形.∴
∠ABD=60°.∴
易得∠OBH=30°.∴
OH=OB=1.∴
OG==.∴
CF=CG=OC+OG=OB+OG=2+
如图.(1)
∵
点I是△ABC的内心,∴
∠2=∠7=∠ABC.∵
DG平分∠ADF,∴
∠1=∠ADF.∵
∠ADF=∠ABC,∴
∠1=∠2.∵
∠3=∠2,∴
∠1=∠3.∴
DG∥AC (2)
∵
∠2=∠7,∠2=∠3,∴
∠7=∠3.∵
点I是△ABC的内心,∴
∠5=∠6.∵
∠4=∠7+∠5=∠3+∠6,∴
∠4=∠DAI.∴
AD=ID (3)
∵
DE=4,BE=5,∴
BD=DE+BE=9.∵
∠3=∠7,∠ADE=∠BDA,∴
△DAE∽△DBA.∴
=.∴
AD2=BD·DE=9×4=36.∴
AD=6(负值舍去).∴
DI=6.∴
BI=BD-DI=9-6=3
(1)
如图,连接OC.∵
D为的中点,∴
=.∴
∠DOB=∠DOC.∴
∠DOB=∠BOC.∵
∠A=∠BOC,∴
∠A=∠DOB (2)
DE与⊙O相切 理由:∵
∠A=∠DOB,∴
AE∥OD.∵
DE⊥AE,∴
OD⊥DE.∵
OD是⊙O的半径,∴
DE与⊙O相切.
(1)
如图①,连接OC.∵
CD∥AB,BC∥OD,∴
四边形BODC是平行四边形.∴
OB=CD.∵
OA=OB,∴
CD=OA.∴
四边形AOCD是平行四边形.∵
AF为半圆O的切线,∴
AB⊥AD,即∠A=90°.∴
四边形AOCD是矩形.∴
∠OCD=90°,即OC⊥CD.∵
OC是半圆O的半径,∴
CD是半圆O的切线 (2)
∠AED+∠ACD=90°.如图②,连接BE.∵
AB为半圆O的直径,∴
∠AEB=90°.∴
∠EBA+∠BAE=90°.∵
AD是半圆O的切线,∴
AB⊥AD,即∠BAD=90°.∴
∠DAE+∠BAE=90°.∴
∠ABE=∠DAE.∵
∠ACE=∠ABE,∴
∠ACE=∠DAE.∵
CD∥AB,∴
∠ADE=180°-∠BAD=90°.∴
∠AED+∠DAE=90°.∴
∠AED+∠ACD=90°
(1)
直线DE与⊙O相切 理由:如图,连接OD.∵
AD平分∠BAC,∴
∠OAD=∠CAD.∵
OA=OD,∴
∠OAD=∠ODA.∴
∠ODA=∠CAD.∴
OD∥AC.∵
DE⊥AC,∴
DE⊥OD.∵
OD是⊙O的半径,∴
直线DE与⊙O相切. (2)
如图,连接OF.∵
∠BAC=60°,OA=OF=2,∴
△AOF是等边三角形.∴
AF=OA=OD.∵
AF∥OD,∴
四边形AODF是平行四边形.∴
DF∥OA,DF=OA=2.∴
∠EFD=∠BAC=60°.∵
DE⊥AC,∴
∠AED=90°.∴
∠EDF=30°.∴
EF=DF=1
(1)
如图,连接OM.∵
OM=OB,∴
∠OMB=∠OBM.∵
BM平分∠ABD,∴
∠OBM=∠MBF.∴
∠OMB=∠MBF.∴
OM∥BF.∵
MF⊥BD,∴
OM⊥MF.∵
OM是⊙O的半径,∴
MF是⊙O的切线 (2)
∵
=,∴
∠CBN=∠BMN.∵
∠N=∠N,∴
△CBN∽△BMN.∴
=,即=,解得MN=.∴
CM=MN-CN=-3=
(1)
如图,连接OC.∵
OE∥AC,∴
∠OEB=∠ACB.∵
AB是⊙O的直径,∴
∠OEB=∠ACB=90°.∴
OD⊥BC.∴
CE=BE,即OD垂直平分BC.∴
DB=DC.∴
∠DBE=∠DCE.又∵
OC=OB,∴
∠OBE=∠OCE.∴
∠DBE+∠OBE=∠DCE+∠OCE,即∠DBO=∠OCD.∵
DB为⊙O的切线,∴
OB⊥BD,即∠DBO=90°.∴
∠OCD=∠DBO=90°,即OC⊥DC.∵
OC是⊙O的半径,∴
DC是⊙O的切线 (2)
在Rt△ABC中,∵
∠ABC=30°,∴
∠CAO=60°.又∵
OA=OC,∴
△AOC是等边三角形.∴
∠COF=60°.∵
AB=8,∴
OC=4.在Rt△COF中,tan
∠COF=,∴
CF=OC·tan
∠COF=4×=4
(1)
∵
AF与⊙O相切于点A,∴
OA⊥AF,即∠OAF=90°.∴
∠F=30°,∴
∠AOB=180°-∠OAF-∠F=180°-90°-30°=60°.∴
∠ADB=∠AOB=30° (2)
∵
BD是⊙O的直径,∴
∠BAD=90°.∵
∠BAC=120°,∴
∠DAC=30°.∴
∠DBC=∠DAC=30°.∵
∠F=30°,∴
∠F=∠DBC.∴
AF∥BC.∵
OA⊥AF,∴
OA⊥BC.∴
BE=CE=BC=4,AB=AC.∵
∠AOB=60°,OA=OB,∴
△AOB是等边三角形.∴
AB=OB.在Rt△BOE中,∵
∠OBE=30°,∴
OB===.∴
AC=AB=OB=
(1)
如图,过点D作DF⊥BC于点F,连接DB.∵
AP是⊙O的切线,∴
PA⊥AC,即∠PAC=90°.∴
∠APC+∠ACP=90°.∵
AC是⊙O的直径,∴
∠ADC=90°.∴
∠ACP+∠DAC=90°.∴
∠APC=∠DAC.∵
∠DAC=∠DBC,∠APC=∠BCP,∴
∠DBC=∠DCB.∴
DB=DC.∵
DF⊥BC,∴
BF=CF,∠BDC=2∠ODC.∴
易得DF经过圆心O.∵
OD=OC,∴
∠ODC=∠OCD.∴
∠BAC=∠BDC=2∠ODC=2∠OCD.∴
∠BAC=2∠ACD (2)
由(1),得CF=BC=3.∵
DE⊥AC,∴
∠DEC=∠CFD=90°.∵
∠ADC=90°,∴
∠CDF+∠ADO=90°,∠DCE+∠DAO=90°.∵
OA=OD,∴
∠ADO=∠DAO.∴
∠CDF=∠DCE.在△DEC和△CFD中,∴
△DEC≌△CFD.∴
DE=CF=3.易得△CDE∽△DAE,∴
=.∴
CE==.∴
AC=AE+CE=2+=.∴
OA=AC=.∴
⊙O的半径为
12
一、
选择题
1.
(2019·重庆)如图,AB是⊙O的直径,AC是⊙O的切线,A为切点.若∠C=40°,则∠B的度数为( )
A.
60°
B.
50°
C.
40°
D.
30°
2.
(2019·苏州)如图,AB为⊙O的切线,切点为A,连接AO,BO,BO与⊙O交于点C,延长BO与⊙O交于点D,连接AD.
若∠ABO=36°,则∠ADC的度数为( )
A.
54°
B.
36°
C.
32°
D.
27°
3.
(2019·重庆)如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.
若∠C=50°,则∠AOD的度数为( )
A.
40°
B.
50°
C.
80°
D.
100°
4.
(2019·无锡)如图,PA是⊙O的切线,切点为A,PO的延长线交⊙O于点B.若∠P=40°,则∠B的度数为( )
A.
20°
B.
25°
C.
40°
D.
50°
5.
(2018·鄂尔多斯)以O为中心点的量角器与直角三角尺ABC按如图所示的方式摆放,直角顶点B在零刻度线所在直线DE上,且量角器与三角尺只有一个公共点P,则∠CBD的度数是( )
A.
45°10′
B.
44°50′
C.
46°10′
D.
无法确定
6.
(2019·舟山)如图,⊙O上有三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC的延长线于点P,则PA的长为( )
A.
2
B.
C.
D.
7.
(2019·广州)平面内,⊙O的半径为1,点P到点O的距离为2,过点P可作的⊙O的切线有( )
A.
0条
B.
1条
C.
2条
D.
无数条
8.
(2019·杭州)如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB的长为( )
A.
2
B.
3
C.
4
D.
5
9.
(2019·益阳)如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D.下列结论不一定成立的是( )
A.
PA=PB
B.
∠BPD=∠APD
C.
AB⊥PD
D.
AB平分PD
10.
(2019·哈尔滨)如图,PA,PB分别与⊙O相切于A,B两点,C为⊙O上一点,连接AC,BC.若∠P=50°,则∠ACB的度数为( )
A.
60°
B.
75°
C.
70°
D.
65°
11.
(2019·福建)如图,PA,PB是⊙O的切线,A,B为切点,点C在⊙O上,且∠ACB=55°,则∠APB的度数为( )
A.
55°
B.
70°
C.
110°
D.
125°
12.
(2019·台州)如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( )
A.
2
B.
3
C.
4
D.
4-
13.
(2019·台湾)如图,Rt△ABC的内切圆分别与AB,BC相切于点D,E.根据图中标示的长度与角度,则AD的长为( )
A.
B.
C.
D.
14.
(2019·泰安)如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO的延长线于点P,则∠P的度数为( )
A.
32°
B.
31°
C.
29°
D.
61°
15.
(2019·台湾)如图,△ABC的顶点B,C皆在直线l上,且其内心为点I.今固定点C,将此三角形按顺时针方向旋转,使得△A′B′C的顶点A′落在直线l上,且其内心为点I′.若∠A<∠B<∠C,则下列说法正确的是( )
A.
IC和I′A′平行,II′和l平行
B.
IC和I′A′平行,II′和l不平行
C.
IC和I′A′不平行,II′和l平行
D.
IC和I′A′不平行,II′和l不平行
二、
填空题
16.
(2019·河池)如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=________.
17.
(2019·南京)如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上.若∠P=102°,则∠A+∠C=________.
18.
(2019·宿迁)直角三角形的两条直角边分别是5和12,则它的内切圆半径为________.
19.
(2019·荆州)如图,AB为⊙O的直径,C为⊙O上一点,过点B的切线交AC的延长线于点D,E为弦AC的中点,AD=10,BD=6.若P为直径AB上的一个动点,连接EP,当△AEP是直角三角形时,AP的长为__________.
20.
(2019·菏泽)如图,直线y=-x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,1个单位长度为半径作⊙P.当⊙P与直线AB相切时,点P的坐标是__________________.
三、
解答题
21.
(2019·贵阳)如图,AB是⊙O的直径,P是⊙O上一点,连接OP,点A关于OP的对称点C恰好落在⊙O上.
(1)
求证:OP∥BC.
(2)
过点C作⊙O的切线CD,交AP的延长线于点D.
如果∠D=90°,DP=1,求⊙O的直径.
第21题
22.
(2019·玉林)如图,在△ABC中,AB=AC=5,BC=6,以AB为直径作⊙O分别交AC,BC于点D,E,过点E作⊙O的切线EF交AC于点F,连接BD.
(1)
求证:EF是△CDB的中位线;
(2)
求EF的长.
第22题
23.
(2019·河池)如图,五边形ABCDE内接于⊙O,CF与⊙O相切于点C,交AB的延长线于点F.
(1)
若AE=DC,∠E=∠BCD,求证:DE=BC;
(2)
若OB=2,AB=BD=DA,∠F=45°,求CF的长.
第23题
24.
(2019·孝感)如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.
(1)
求证:DG∥CA;
(2)
求证:AD=ID;
(3)
若DE=4,BE=5,求BI的长.
第24题
25.
(2019·徐州)如图,AB为⊙O的直径,C为⊙O上一点,D为的中点.过点D作直线AC的垂线,垂足为E,连接OD.
(1)
求证:∠A=∠DOB.
(2)
DE与⊙O有怎样的位置关系?请说明理由.
第25题
26.
(2019·江西)如图①,AB为半圆O的直径,AF为半圆O的切线,过半圆O上的点C作CD∥AB交AF于点D,连接BC.
(1)
连接DO,若BC∥OD,求证:CD是半圆O的切线;
(2)
如图②,当线段CD与半圆O交于点E时,连接AE,AC,判断∠AED和∠ACD之间的数量关系,并证明你的结论.
27.
(2019·淮安)如图,AB是⊙O的直径,AC与⊙O交于点F,弦AD平分∠BAC,DE⊥AC,垂足为E.
(1)
试判断直线DE与⊙O的位置关系,并说明理由;
(2)
若⊙O的半径为2,∠BAC=60°,求线段EF的长.
第27题
28.
(2019·锦州)如图,M,N是以AB为直径的⊙O上的点,且=,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
(1)
求证:MF是⊙O的切线;
(2)
若CN=3,BN=4,求CM的长.
第28题
29.
(2019·雅安)如图,AB是⊙O的直径,AC,BC是⊙O的弦,OE∥AC交BC于点E,过点B作⊙O的切线交OE的延长线于点D,连接DC并延长,交BA的延长线于点F.
(1)
求证:DC是⊙O的切线;
(2)
若∠ABC=30°,AB=8,求线段CF的长.
第29题
30.
(2019·贺州)如图,BD是⊙O的直径,弦BC与OA相交于点E,AF与⊙O相切于点A,交DB的延长线于点F,∠F=30°,∠BAC=120°,BC=8.
求:
(1)
∠ADB的度数;
(2)
AC的长.
第30题
31.
(2019·大连)如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点A的切线与CD的延长线相交于点P,且∠APC=∠BCP.
(1)
求证:∠BAC=2∠ACD.
(2)
过点D作DE⊥AC,垂足为E.当BC=6,AE=2时,求⊙O的半径.
第31题
参考答案
一、
B
D
C
B
D
B
C
B
D
D
B
A
D
A
C
二、
76°
219°
2
4或2.56
或
三、
(1)
∵
点A关于OP的对称点C恰好落在⊙O上.∴
=.∴
∠AOP=∠COP.∴
∠AOP=∠AOC.又∵
∠ABC=∠AOC,∴
∠AOP=∠ABC.∴
OP∥BC (2)
如图,连接PC.∵
CD为⊙O的切线,∴
OC⊥CD,即∠OCD=90°.又∵
∠D=90°,∴
∠OCD+∠D=180°.∴
OC∥AD.∴
∠APO=∠COP.∵
∠AOP=∠COP,∴
∠APO=∠AOP.∴
OA=AP.∵
OA=OP,∴
OA=AP=OP.∴
△APO为等边三角形.∴
∠AOP=60°.∴
∠COP=∠AOP=60°.∵
OP=OC,∴
△POC为等边三角形.∴
∠PCO=60°,PC=OP.又∵
∠OCD=90°,∴
∠PCD=30°.∵
DP=1,∠D=90°,∴
PC=2DP=2.∴
AB=2OP=2PC=4.∴
⊙O的直径为4
(1)
如图,连接AE,OE.∵
AB为⊙O的直径,∴
∠ADB=∠AEB=90°.∴
BD⊥AC,AE⊥BC.又∵
AB=AC,∴
BE=CE=3.∵
EF是⊙O的切线,∴
OE⊥EF.∵
OA=OB,∴
OE是△ABC的中位线.∴
OE∥AC.∴
OE⊥BD.∴
BD∥EF.∵
BE=CE,∴
易得CF=DF.∴
EF是△CDB的中位线 (2)
∵
∠AEB=90°,∴
AE===4.∵
S△ABC=AC·BD=BC·AE,∴
BD===.∵
EF是△CDB的中位线,∴
EF=BD=
(1)
∵
AE=DC,∴
∠ADE=∠DBC.在△ADE和△DBC中,∴
△ADE≌△DBC.∴
DE=BC (2)
如图,连接CO并延长,交AB于点G,过点O作OH⊥AB于点H.∴
∠OHG=∠OHB=90°.∵
CF与⊙O相切于点C,∴
OC⊥FC,即∠FCG=90°.∵
∠F=45°,∴
易得△CFG,△OGH是等腰直角三角形.∴
CF=CG,OH=HG.∵
AB=BD=DA,∴
△ABD是等边三角形.∴
∠ABD=60°.∴
易得∠OBH=30°.∴
OH=OB=1.∴
OG==.∴
CF=CG=OC+OG=OB+OG=2+
如图.(1)
∵
点I是△ABC的内心,∴
∠2=∠7=∠ABC.∵
DG平分∠ADF,∴
∠1=∠ADF.∵
∠ADF=∠ABC,∴
∠1=∠2.∵
∠3=∠2,∴
∠1=∠3.∴
DG∥AC (2)
∵
∠2=∠7,∠2=∠3,∴
∠7=∠3.∵
点I是△ABC的内心,∴
∠5=∠6.∵
∠4=∠7+∠5=∠3+∠6,∴
∠4=∠DAI.∴
AD=ID (3)
∵
DE=4,BE=5,∴
BD=DE+BE=9.∵
∠3=∠7,∠ADE=∠BDA,∴
△DAE∽△DBA.∴
=.∴
AD2=BD·DE=9×4=36.∴
AD=6(负值舍去).∴
DI=6.∴
BI=BD-DI=9-6=3
(1)
如图,连接OC.∵
D为的中点,∴
=.∴
∠DOB=∠DOC.∴
∠DOB=∠BOC.∵
∠A=∠BOC,∴
∠A=∠DOB (2)
DE与⊙O相切 理由:∵
∠A=∠DOB,∴
AE∥OD.∵
DE⊥AE,∴
OD⊥DE.∵
OD是⊙O的半径,∴
DE与⊙O相切.
(1)
如图①,连接OC.∵
CD∥AB,BC∥OD,∴
四边形BODC是平行四边形.∴
OB=CD.∵
OA=OB,∴
CD=OA.∴
四边形AOCD是平行四边形.∵
AF为半圆O的切线,∴
AB⊥AD,即∠A=90°.∴
四边形AOCD是矩形.∴
∠OCD=90°,即OC⊥CD.∵
OC是半圆O的半径,∴
CD是半圆O的切线 (2)
∠AED+∠ACD=90°.如图②,连接BE.∵
AB为半圆O的直径,∴
∠AEB=90°.∴
∠EBA+∠BAE=90°.∵
AD是半圆O的切线,∴
AB⊥AD,即∠BAD=90°.∴
∠DAE+∠BAE=90°.∴
∠ABE=∠DAE.∵
∠ACE=∠ABE,∴
∠ACE=∠DAE.∵
CD∥AB,∴
∠ADE=180°-∠BAD=90°.∴
∠AED+∠DAE=90°.∴
∠AED+∠ACD=90°
(1)
直线DE与⊙O相切 理由:如图,连接OD.∵
AD平分∠BAC,∴
∠OAD=∠CAD.∵
OA=OD,∴
∠OAD=∠ODA.∴
∠ODA=∠CAD.∴
OD∥AC.∵
DE⊥AC,∴
DE⊥OD.∵
OD是⊙O的半径,∴
直线DE与⊙O相切. (2)
如图,连接OF.∵
∠BAC=60°,OA=OF=2,∴
△AOF是等边三角形.∴
AF=OA=OD.∵
AF∥OD,∴
四边形AODF是平行四边形.∴
DF∥OA,DF=OA=2.∴
∠EFD=∠BAC=60°.∵
DE⊥AC,∴
∠AED=90°.∴
∠EDF=30°.∴
EF=DF=1
(1)
如图,连接OM.∵
OM=OB,∴
∠OMB=∠OBM.∵
BM平分∠ABD,∴
∠OBM=∠MBF.∴
∠OMB=∠MBF.∴
OM∥BF.∵
MF⊥BD,∴
OM⊥MF.∵
OM是⊙O的半径,∴
MF是⊙O的切线 (2)
∵
=,∴
∠CBN=∠BMN.∵
∠N=∠N,∴
△CBN∽△BMN.∴
=,即=,解得MN=.∴
CM=MN-CN=-3=
(1)
如图,连接OC.∵
OE∥AC,∴
∠OEB=∠ACB.∵
AB是⊙O的直径,∴
∠OEB=∠ACB=90°.∴
OD⊥BC.∴
CE=BE,即OD垂直平分BC.∴
DB=DC.∴
∠DBE=∠DCE.又∵
OC=OB,∴
∠OBE=∠OCE.∴
∠DBE+∠OBE=∠DCE+∠OCE,即∠DBO=∠OCD.∵
DB为⊙O的切线,∴
OB⊥BD,即∠DBO=90°.∴
∠OCD=∠DBO=90°,即OC⊥DC.∵
OC是⊙O的半径,∴
DC是⊙O的切线 (2)
在Rt△ABC中,∵
∠ABC=30°,∴
∠CAO=60°.又∵
OA=OC,∴
△AOC是等边三角形.∴
∠COF=60°.∵
AB=8,∴
OC=4.在Rt△COF中,tan
∠COF=,∴
CF=OC·tan
∠COF=4×=4
(1)
∵
AF与⊙O相切于点A,∴
OA⊥AF,即∠OAF=90°.∴
∠F=30°,∴
∠AOB=180°-∠OAF-∠F=180°-90°-30°=60°.∴
∠ADB=∠AOB=30° (2)
∵
BD是⊙O的直径,∴
∠BAD=90°.∵
∠BAC=120°,∴
∠DAC=30°.∴
∠DBC=∠DAC=30°.∵
∠F=30°,∴
∠F=∠DBC.∴
AF∥BC.∵
OA⊥AF,∴
OA⊥BC.∴
BE=CE=BC=4,AB=AC.∵
∠AOB=60°,OA=OB,∴
△AOB是等边三角形.∴
AB=OB.在Rt△BOE中,∵
∠OBE=30°,∴
OB===.∴
AC=AB=OB=
(1)
如图,过点D作DF⊥BC于点F,连接DB.∵
AP是⊙O的切线,∴
PA⊥AC,即∠PAC=90°.∴
∠APC+∠ACP=90°.∵
AC是⊙O的直径,∴
∠ADC=90°.∴
∠ACP+∠DAC=90°.∴
∠APC=∠DAC.∵
∠DAC=∠DBC,∠APC=∠BCP,∴
∠DBC=∠DCB.∴
DB=DC.∵
DF⊥BC,∴
BF=CF,∠BDC=2∠ODC.∴
易得DF经过圆心O.∵
OD=OC,∴
∠ODC=∠OCD.∴
∠BAC=∠BDC=2∠ODC=2∠OCD.∴
∠BAC=2∠ACD (2)
由(1),得CF=BC=3.∵
DE⊥AC,∴
∠DEC=∠CFD=90°.∵
∠ADC=90°,∴
∠CDF+∠ADO=90°,∠DCE+∠DAO=90°.∵
OA=OD,∴
∠ADO=∠DAO.∴
∠CDF=∠DCE.在△DEC和△CFD中,∴
△DEC≌△CFD.∴
DE=CF=3.易得△CDE∽△DAE,∴
=.∴
CE==.∴
AC=AE+CE=2+=.∴
OA=AC=.∴
⊙O的半径为
