鲁教版(五四制)八年级数学上学期《5.2 平行四边形的判定》同步练习试题(Word版 含答案)
文档属性
| 名称 | 鲁教版(五四制)八年级数学上学期《5.2 平行四边形的判定》同步练习试题(Word版 含答案) | 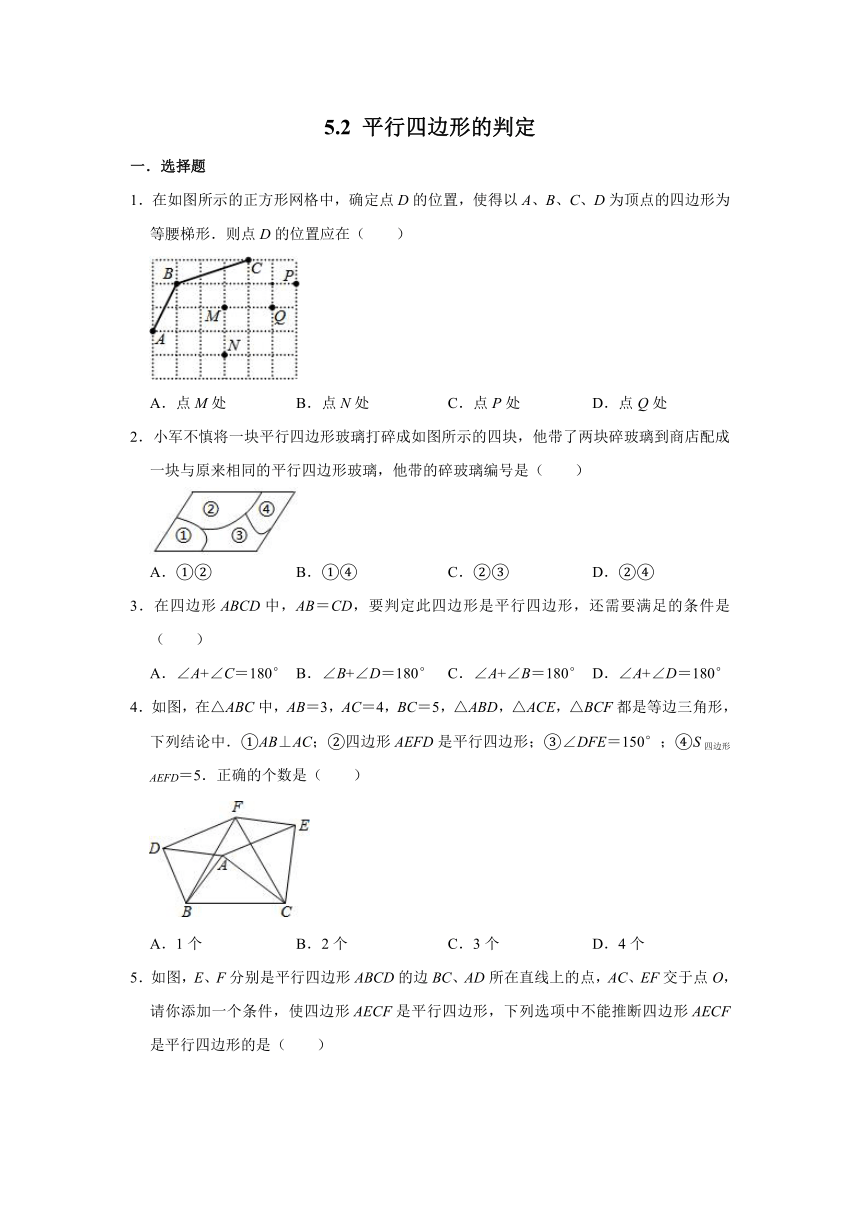 | |
| 格式 | zip | ||
| 文件大小 | 194.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 14:43:37 | ||
图片预览





文档简介
5.2
平行四边形的判定
一.选择题
1.在如图所示的正方形网格中,确定点D的位置,使得以A、B、C、D为顶点的四边形为等腰梯形.则点D的位置应在( )
A.点M处
B.点N处
C.点P处
D.点Q处
2.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①②
B.①④
C.②③
D.②④
3.在四边形ABCD中,AB=CD,要判定此四边形是平行四边形,还需要满足的条件是( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
4.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中.①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=5.正确的个数是( )
A.1个
B.2个
C.3个
D.4个
5.如图,E、F分别是平行四边形ABCD的边BC、AD所在直线上的点,AC、EF交于点O,请你添加一个条件,使四边形AECF是平行四边形,下列选项中不能推断四边形AECF是平行四边形的是( )
A.AE=CF
B.EO=FO
C.AE∥CF
D.AF=EC
6.如图,在四边形ABCD中,AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,若DE=BF,则下列结论不一定正确的是( )
A.CF=AE
B.OE=OF
C.△CDE为直角三角形
D.四边形ABCD是平行四边形
二.填空题
7.如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为1cm/s,过点P的直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<2.5),当t为
时,以P、Q、D、M为顶点的四边形是平行四边形.
8.如图,在?ABCD中,已知AD=15cm,点P在AD边上以1cm/s的速度从点A向点D运动,点Q在BC边上以4cm/s的速度从点C出发在BC上往返运动,两个点同时出发,当点P到达点D时停止运动(同时Q点也停止),设运动时间为t(s)(t>0),若以P,D,Q,B四点为顶点的四边形是平行四边形,则t的值可以是
.
9.如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=3,则GE=
.
三.解答题
10.如图,已知BE∥DF,∠ADF=∠CBE,AD=BC.求证:四边形DEBF是平行四边形.
11.如图,在四边形ABCD中,AB∥CD,∠BAD的平分线AE交CD于点F,交BC的延长线于点E,且AB=BE.
(1)求证:四边形ABCD是平行四边形;
(2)连结BF,若BF⊥AE,∠E=60°,AB=6,求四边形ABCD的面积.
12.如图,在四边形ABCD中,AC、BD交于点O,AE⊥BD,CF⊥BD,E、F分别为垂足,BE=DF,AF∥CE.
(1)试判断四边形AECF、四边形ABCD形状,并说明理由;
(2)如果AF=10,EF=8,BE=7,求BC.
13.图,点E、F分别在?ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,判断四边形AECF的形状并证明.
14.如图,?ABCD中,延长BC至E,使得CE=BC,连接DE,F是AD的中点,连接CF.
(1)求证:四边形CEDF是平行四边形:
(2)若AB=8,AD=10,∠B=60°,求四边形ABCF的面积.
15.如图,在四边形ABCD中,点E在BC上,点F在AD上,BD与EF相交于点O,并且互相平分,AF=CE.求证:四边形ABCD是平行四边形.
16.如图,AD、BF相交于点O,点E、C在BF上,BE=FC,AC=DE,AB=DF,求证:四边形ABDF是平行四边形.
17.如图,在四边形ABCD中,对角线AC与BD相交于点O,点O是BD的中点.点E、F在对角线AC上,连接DE、BF,DE∥BF,AE=CF.
求证:四边形ABCD是平行四边形.
18.如图,点E为?ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF.
(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;
(2)求证:四边形AFHD为平行四边形;
(3)连接EH,交BC于点O,若OC=OH,求证:EF⊥EG.
19.已知梯形ABCD中,AD∥BC,AB=AD=DC,点E、F分别是对角线AC、BD的中点.求证:四边形ADEF为等腰梯形.
参考答案
一.选择题
1.解:①若AB为底,如图所示:
此时没有符合题意的点D.
②若AB为腰,如图所示:
此时符合题意的点为点P.
故选:C.
2.解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选:C.
3.解:A、添加∠A+∠C=180°不能判定此四边形是平行四边形,故此选项不合题意;
B、添加∠B+∠D=180°不能判定此四边形是平行四边形,故此选项不合题意;
C、添加∠A+∠B=180°可得AD∥CB,再加上AB=CD不能判定此四边形是平行四边形,故此选项不符合题意;
D、添加∠A+∠D=180°可得AB∥CD,再加上AB=CD可判定此四边形是平行四边形,故此选项符合题意;
故选:D.
4.解:∵32+42=52,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴S?AEFD=AD?(DF?sin30°)=3×(4×)=6,故④不正确;
∴正确的个数是3个,
故选:C.
5.解:∵四边形ABCD是平行四边形,
∴AD∥BC,即AF∥EC.
A.AE=CF时,一组对边平行,另一组对边相等不能判定四边形AECF为平行四边形;
B.EO=FO,又∵AO=CO,∴四边形AECF为平行四边形;
C.∵AE∥CF,AF∥EC,∴四边形AECF是平行四边形;
D.∵AF∥EC,AF=EC,∴四边形AECF是平行四边形.
故选:A.
6.解:∵AE⊥BD于点E,CF⊥BD于点F,
∴∠DFC=∠BEA=90°,
∵DE=BF,
∴DE﹣EF=BF﹣EF,
即DF=BE,
在Rt△DCF和Rt△BAE中,,
∴Rt△DCF≌Rt△BAE(HL),
∴CF=AE,故选项A不符合题意;
∵AE⊥BD于点E,CF⊥BD于点F,
∴AE∥FC,
∵CF=AE,
∴四边形CFAE是平行四边形,
∴OE=OF,故选项B不符合题意;
∵Rt△DCF≌Rt△BAE,
∴∠CDF=∠ABE,
∴CD∥AB,
∵CD=AB,
∴四边形ABCD是平行四边形,故选项D不符合题意;
无法证明△CDE为直角三角形,故选项C符合题意;
故选:C.
二.填空题
7.解:如图1所示:
∵BD⊥AC,
∴AD===6,
∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
分两种情况:
①当点M在点D的上方时,如图2所示:
由题意得:PQ=BP=t,AM=4t,AD=6,
∴MD=AD﹣AM=6﹣4t,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=6﹣4t时,四边形PQDM是平行四边形,
解得:t=(s);
②当点M在点D的下方时,如图3所示:
根据题意得:PQ=BP=t,AM=4t,AD=6,
∴MD=AM﹣AD=4t﹣6,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=4t﹣6时,四边形PQDM是平行四边形,
解得:t=2(s);
综上所述,当t=s或t=2s时,以P、Q、D、M为顶点的四边形为平行四边形;
故答案为:s或2s.
8.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵P在AD上运动,
∴t≤=15,即t≤15,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B﹣C,方程为4t﹣15=15﹣t,
解得:t=6;
②点Q的运动路线是C﹣B﹣C﹣B,方程为15﹣(4t﹣30)=15﹣t,
解得:t=10;
③点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣45=15﹣t,
解得:t=12;
故答案为:6或10或12.
9.解:取BE的中点H,连接FH、CH,如图:
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,FH=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E是CD的中点,
∴EC=CD,
∴FH∥EC,FH=EC,
∴四边形FHCE是平行四边形,
∴GE=GH=EH.
∵BE=3,H是BE的中点,
∴EH=,
∴GE=.
故答案为:.
三.解答题
10.证明:∵BE∥DF,
∴∠BEF=∠DFE,
又∵∠ADF=∠CBE,AD=BC,
∴△BEF≌△DFE(AAS),
∴BE=DF,
∴四边形BFDE是平行四边形.
11.证明:(1)∵AB=BE,
∴∠E=∠BAE,
∵AF平分∠BAD,
∴∠DAF=∠BAE,
∴∠DAF=∠E,
∴AD∥BE,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2)∵AB=BE,∠E=60°,
∴△ABE是等边三角形,
∴BA=AE=6,∠BAE=60°,
又∵BF⊥AE,
∴AF=EF=3,
∴BF===3,
∴S△ABF=AF×BF=×3×3=,
∴?ABCD的面积=2×S△ABF=9.
12.解:(1)四边形AECF、四边形ABCD都是平行四边形,理由如下:
∵AE⊥BD,CF⊥BD,
∴AE∥CF,
∵AF∥CE,
∴四边形AECF是平行四边形;
∴OA=OC,OE=OF,
又∵BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形;
(2)由(1)得:四边形AECF是平行四边形,
∴AE=CF,
在Rt△AEF中,AE===6,
∴CF=6,
∵BE=7,EF=8,
∴BF=BE+EF=15,
在Rt△BCF中,BC===3.
13.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又∵BE=DF,
∴AB+BE=DC+DF,
即AE=CF.
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
∴AC、EF互相平分.
(2)四边形AECF是菱形.
证明:∵AB∥DC,
∴∠AEO=∠CFO.
∵EF平分∠AEC,
∴∠AEO=∠CEO.
∴∠CEO=∠CFO.
∴CE=CF.
∵四边形AECF是平行四边形,
∴四边形AECF是菱形.
14.(1)证明:在?ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴AF=DF=AD.
又∵CE=BC,
∴DF=CE,
∵DF∥CE,
∴四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H.
在?ABCD中,∵∠B=60°,AD∥BC,
∴∠B=∠DCE,CD=AB=8,BC=AD=10,
∴∠DCE=60°.
∴∠CDH=30°,
∴CH=CD=4,DH=CH=4,
由(1)得:AF=AD=5,
∴四边形ABCF的面积=(AF+BC)×DH=(5+10)×4=30.
15.证明:连接BF、DE,
∵BD与EF互相平分,
∴四边形BFDE是平行四边形,
∴DF∥BE,DF=BE,
∵AF=CE,
∴AD=BC,
∴四边形ABCD是平行四边形.
16.证明:连接AF、BD,如图所示:
∵BE=CF,
∴BE+CE=CF+CE,即BC=FE.
在△ABC和△DFE中,,
∴△ABC≌△DFE(SSS),
∴AB=DF,∠ABF=∠DFE,
∴AB∥DF,
∴四边形ABDF是平行四边形.
17.证明:∵DE∥BF,
∴∠EDO=∠FBO,
∵点O是BD的中点,
∴OD=OB,
在△DEO与△BFO中,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∵AE=CF,
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形.
18.(1)解:∵四边形ABCD是平行四边形,
∴∠BAE=∠BCD=70°,AD∥BC,
∵∠DCE=20°,AB∥CD,
∴∠CDE=180°﹣∠BAE=110°,
∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAE=∠BCD,
∵BF=BE,CG=CE,
∴BC是△EFG的中位线,
∴BC∥FG,BC=FG,
∵H为FG的中点,
∴FH=FG,
∴BC∥FH,BC=FH,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(3)证明:连接EH,CH,
∵CE=CG,FH=HG,
∴CH=EF,CH∥EF,
∵EB=BF=EF,
∴BE=CH,
∴四边形EBHC是平行四边形,
∴OB=OC,OE=OH,
∵OC=OH,
∴OE=OB=OC=BC,
∴△BCE是直角三角形,
∴∠FEG=90°,
∴EF⊥EG.
19.证明:∵AD∥BC,AB=DC,
∴AC=BD,
∵点E、F分别是对角线AC、BD的中点,
∴DF=BD,AE=AC,
∴DF=AE,
∵AB=AD=DC,点E、F分别是对角线AC、BD的中点,
∴AF⊥BD,DE⊥AC,
在Rt△ADF和Rt△DAE中,
∵,
∴△ADF≌△DAE(HL),
∴∠DAE=∠ADF,AF=DE,
在△AFE和△DEF中,
∵,
∴△AFE≌△DEF(SSS),
∴∠AEF=∠DFE,
设对角线交于点O,
∴∠AOD=180°﹣∠DAE﹣∠ADF=180°﹣2∠DAE,∠EOF=180°﹣∠AEF﹣∠DFE=180°﹣2∠AEF,
∵∠AOD=∠EOF,
∴∠DAE=∠AEF,
∴EF∥AD,
∵AF⊥BD,DE⊥AC,
∴∠DAF和∠ADE都是锐角,
∴AF与DE不平行,
∴ADEF为梯形,
又DF=AE,
∴ADEF为等腰梯形.
平行四边形的判定
一.选择题
1.在如图所示的正方形网格中,确定点D的位置,使得以A、B、C、D为顶点的四边形为等腰梯形.则点D的位置应在( )
A.点M处
B.点N处
C.点P处
D.点Q处
2.小军不慎将一块平行四边形玻璃打碎成如图所示的四块,他带了两块碎玻璃到商店配成一块与原来相同的平行四边形玻璃,他带的碎玻璃编号是( )
A.①②
B.①④
C.②③
D.②④
3.在四边形ABCD中,AB=CD,要判定此四边形是平行四边形,还需要满足的条件是( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
4.如图,在△ABC中,AB=3,AC=4,BC=5,△ABD,△ACE,△BCF都是等边三角形,下列结论中.①AB⊥AC;②四边形AEFD是平行四边形;③∠DFE=150°;④S四边形AEFD=5.正确的个数是( )
A.1个
B.2个
C.3个
D.4个
5.如图,E、F分别是平行四边形ABCD的边BC、AD所在直线上的点,AC、EF交于点O,请你添加一个条件,使四边形AECF是平行四边形,下列选项中不能推断四边形AECF是平行四边形的是( )
A.AE=CF
B.EO=FO
C.AE∥CF
D.AF=EC
6.如图,在四边形ABCD中,AB=CD,对角线AC、BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF、CE,若DE=BF,则下列结论不一定正确的是( )
A.CF=AE
B.OE=OF
C.△CDE为直角三角形
D.四边形ABCD是平行四边形
二.填空题
7.如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为1cm/s,过点P的直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<2.5),当t为
时,以P、Q、D、M为顶点的四边形是平行四边形.
8.如图,在?ABCD中,已知AD=15cm,点P在AD边上以1cm/s的速度从点A向点D运动,点Q在BC边上以4cm/s的速度从点C出发在BC上往返运动,两个点同时出发,当点P到达点D时停止运动(同时Q点也停止),设运动时间为t(s)(t>0),若以P,D,Q,B四点为顶点的四边形是平行四边形,则t的值可以是
.
9.如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=3,则GE=
.
三.解答题
10.如图,已知BE∥DF,∠ADF=∠CBE,AD=BC.求证:四边形DEBF是平行四边形.
11.如图,在四边形ABCD中,AB∥CD,∠BAD的平分线AE交CD于点F,交BC的延长线于点E,且AB=BE.
(1)求证:四边形ABCD是平行四边形;
(2)连结BF,若BF⊥AE,∠E=60°,AB=6,求四边形ABCD的面积.
12.如图,在四边形ABCD中,AC、BD交于点O,AE⊥BD,CF⊥BD,E、F分别为垂足,BE=DF,AF∥CE.
(1)试判断四边形AECF、四边形ABCD形状,并说明理由;
(2)如果AF=10,EF=8,BE=7,求BC.
13.图,点E、F分别在?ABCD的边AB、CD的延长线上,且BE=DF,连接AC、EF、AF、CE,AC与EF交于点O.
(1)求证:AC、EF互相平分;
(2)若EF平分∠AEC,判断四边形AECF的形状并证明.
14.如图,?ABCD中,延长BC至E,使得CE=BC,连接DE,F是AD的中点,连接CF.
(1)求证:四边形CEDF是平行四边形:
(2)若AB=8,AD=10,∠B=60°,求四边形ABCF的面积.
15.如图,在四边形ABCD中,点E在BC上,点F在AD上,BD与EF相交于点O,并且互相平分,AF=CE.求证:四边形ABCD是平行四边形.
16.如图,AD、BF相交于点O,点E、C在BF上,BE=FC,AC=DE,AB=DF,求证:四边形ABDF是平行四边形.
17.如图,在四边形ABCD中,对角线AC与BD相交于点O,点O是BD的中点.点E、F在对角线AC上,连接DE、BF,DE∥BF,AE=CF.
求证:四边形ABCD是平行四边形.
18.如图,点E为?ABCD的边AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH,AF.
(1)若∠BAE=70°,∠DCE=20°,求∠DEC的度数;
(2)求证:四边形AFHD为平行四边形;
(3)连接EH,交BC于点O,若OC=OH,求证:EF⊥EG.
19.已知梯形ABCD中,AD∥BC,AB=AD=DC,点E、F分别是对角线AC、BD的中点.求证:四边形ADEF为等腰梯形.
参考答案
一.选择题
1.解:①若AB为底,如图所示:
此时没有符合题意的点D.
②若AB为腰,如图所示:
此时符合题意的点为点P.
故选:C.
2.解:∵只有②③两块角的两边互相平行,且中间部分相联,角的两边的延长线的交点就是平行四边形的顶点,
∴带②③两块碎玻璃,就可以确定平行四边形的大小.
故选:C.
3.解:A、添加∠A+∠C=180°不能判定此四边形是平行四边形,故此选项不合题意;
B、添加∠B+∠D=180°不能判定此四边形是平行四边形,故此选项不合题意;
C、添加∠A+∠B=180°可得AD∥CB,再加上AB=CD不能判定此四边形是平行四边形,故此选项不符合题意;
D、添加∠A+∠D=180°可得AB∥CD,再加上AB=CD可判定此四边形是平行四边形,故此选项符合题意;
故选:D.
4.解:∵32+42=52,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∴AB⊥AC,故①正确;
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°,
∵△ABD和△FBC都是等边三角形,
∴BD=BA,BF=BC,∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC,
在△ABC与△DBF中,,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证:△ABC≌△EFC(SAS),
∴AB=EF=AD=3,
∴四边形AEFD是平行四边形,故②正确;
∴∠DFE=∠DAE=150°,故③正确;
∴∠FDA=180°﹣∠DFE=180°﹣150°=30°,
∴S?AEFD=AD?(DF?sin30°)=3×(4×)=6,故④不正确;
∴正确的个数是3个,
故选:C.
5.解:∵四边形ABCD是平行四边形,
∴AD∥BC,即AF∥EC.
A.AE=CF时,一组对边平行,另一组对边相等不能判定四边形AECF为平行四边形;
B.EO=FO,又∵AO=CO,∴四边形AECF为平行四边形;
C.∵AE∥CF,AF∥EC,∴四边形AECF是平行四边形;
D.∵AF∥EC,AF=EC,∴四边形AECF是平行四边形.
故选:A.
6.解:∵AE⊥BD于点E,CF⊥BD于点F,
∴∠DFC=∠BEA=90°,
∵DE=BF,
∴DE﹣EF=BF﹣EF,
即DF=BE,
在Rt△DCF和Rt△BAE中,,
∴Rt△DCF≌Rt△BAE(HL),
∴CF=AE,故选项A不符合题意;
∵AE⊥BD于点E,CF⊥BD于点F,
∴AE∥FC,
∵CF=AE,
∴四边形CFAE是平行四边形,
∴OE=OF,故选项B不符合题意;
∵Rt△DCF≌Rt△BAE,
∴∠CDF=∠ABE,
∴CD∥AB,
∵CD=AB,
∴四边形ABCD是平行四边形,故选项D不符合题意;
无法证明△CDE为直角三角形,故选项C符合题意;
故选:C.
二.填空题
7.解:如图1所示:
∵BD⊥AC,
∴AD===6,
∵AB=AC,
∴∠ABC=∠C,即∠PBQ=∠C,
∵PQ∥AC,
∴∠PQB=∠C,
∴∠PBQ=∠PQB,
∴PB=PQ;
分两种情况:
①当点M在点D的上方时,如图2所示:
由题意得:PQ=BP=t,AM=4t,AD=6,
∴MD=AD﹣AM=6﹣4t,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=6﹣4t时,四边形PQDM是平行四边形,
解得:t=(s);
②当点M在点D的下方时,如图3所示:
根据题意得:PQ=BP=t,AM=4t,AD=6,
∴MD=AM﹣AD=4t﹣6,
∵PQ∥AC,
∴PQ∥MD,
∴当PQ=MD时,四边形PQDM是平行四边形,
即:当t=4t﹣6时,四边形PQDM是平行四边形,
解得:t=2(s);
综上所述,当t=s或t=2s时,以P、Q、D、M为顶点的四边形为平行四边形;
故答案为:s或2s.
8.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,
∵P在AD上运动,
∴t≤=15,即t≤15,
∵以点P、D、Q、B为顶点组成平行四边形,
∴DP=BQ,
分为以下情况:①点Q的运动路线是C﹣B﹣C,方程为4t﹣15=15﹣t,
解得:t=6;
②点Q的运动路线是C﹣B﹣C﹣B,方程为15﹣(4t﹣30)=15﹣t,
解得:t=10;
③点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣45=15﹣t,
解得:t=12;
故答案为:6或10或12.
9.解:取BE的中点H,连接FH、CH,如图:
∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,FH=AB,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E是CD的中点,
∴EC=CD,
∴FH∥EC,FH=EC,
∴四边形FHCE是平行四边形,
∴GE=GH=EH.
∵BE=3,H是BE的中点,
∴EH=,
∴GE=.
故答案为:.
三.解答题
10.证明:∵BE∥DF,
∴∠BEF=∠DFE,
又∵∠ADF=∠CBE,AD=BC,
∴△BEF≌△DFE(AAS),
∴BE=DF,
∴四边形BFDE是平行四边形.
11.证明:(1)∵AB=BE,
∴∠E=∠BAE,
∵AF平分∠BAD,
∴∠DAF=∠BAE,
∴∠DAF=∠E,
∴AD∥BE,
又∵AB∥CD,
∴四边形ABCD是平行四边形;
(2)∵AB=BE,∠E=60°,
∴△ABE是等边三角形,
∴BA=AE=6,∠BAE=60°,
又∵BF⊥AE,
∴AF=EF=3,
∴BF===3,
∴S△ABF=AF×BF=×3×3=,
∴?ABCD的面积=2×S△ABF=9.
12.解:(1)四边形AECF、四边形ABCD都是平行四边形,理由如下:
∵AE⊥BD,CF⊥BD,
∴AE∥CF,
∵AF∥CE,
∴四边形AECF是平行四边形;
∴OA=OC,OE=OF,
又∵BE=DF,
∴OB=OD,
∴四边形ABCD是平行四边形;
(2)由(1)得:四边形AECF是平行四边形,
∴AE=CF,
在Rt△AEF中,AE===6,
∴CF=6,
∵BE=7,EF=8,
∴BF=BE+EF=15,
在Rt△BCF中,BC===3.
13.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC.
又∵BE=DF,
∴AB+BE=DC+DF,
即AE=CF.
∵AE=CF,AE∥CF,
∴四边形AECF是平行四边形.
∴AC、EF互相平分.
(2)四边形AECF是菱形.
证明:∵AB∥DC,
∴∠AEO=∠CFO.
∵EF平分∠AEC,
∴∠AEO=∠CEO.
∴∠CEO=∠CFO.
∴CE=CF.
∵四边形AECF是平行四边形,
∴四边形AECF是菱形.
14.(1)证明:在?ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴AF=DF=AD.
又∵CE=BC,
∴DF=CE,
∵DF∥CE,
∴四边形CEDF是平行四边形;
(2)如图,过点D作DH⊥BE于点H.
在?ABCD中,∵∠B=60°,AD∥BC,
∴∠B=∠DCE,CD=AB=8,BC=AD=10,
∴∠DCE=60°.
∴∠CDH=30°,
∴CH=CD=4,DH=CH=4,
由(1)得:AF=AD=5,
∴四边形ABCF的面积=(AF+BC)×DH=(5+10)×4=30.
15.证明:连接BF、DE,
∵BD与EF互相平分,
∴四边形BFDE是平行四边形,
∴DF∥BE,DF=BE,
∵AF=CE,
∴AD=BC,
∴四边形ABCD是平行四边形.
16.证明:连接AF、BD,如图所示:
∵BE=CF,
∴BE+CE=CF+CE,即BC=FE.
在△ABC和△DFE中,,
∴△ABC≌△DFE(SSS),
∴AB=DF,∠ABF=∠DFE,
∴AB∥DF,
∴四边形ABDF是平行四边形.
17.证明:∵DE∥BF,
∴∠EDO=∠FBO,
∵点O是BD的中点,
∴OD=OB,
在△DEO与△BFO中,
∴△DEO≌△BFO(ASA),
∴OE=OF,
∵AE=CF,
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形.
18.(1)解:∵四边形ABCD是平行四边形,
∴∠BAE=∠BCD=70°,AD∥BC,
∵∠DCE=20°,AB∥CD,
∴∠CDE=180°﹣∠BAE=110°,
∴∠DEC=180°﹣∠DCE﹣∠CDE=50°;
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠BAE=∠BCD,
∵BF=BE,CG=CE,
∴BC是△EFG的中位线,
∴BC∥FG,BC=FG,
∵H为FG的中点,
∴FH=FG,
∴BC∥FH,BC=FH,
∴AD∥FH,AD=FH,
∴四边形AFHD是平行四边形;
(3)证明:连接EH,CH,
∵CE=CG,FH=HG,
∴CH=EF,CH∥EF,
∵EB=BF=EF,
∴BE=CH,
∴四边形EBHC是平行四边形,
∴OB=OC,OE=OH,
∵OC=OH,
∴OE=OB=OC=BC,
∴△BCE是直角三角形,
∴∠FEG=90°,
∴EF⊥EG.
19.证明:∵AD∥BC,AB=DC,
∴AC=BD,
∵点E、F分别是对角线AC、BD的中点,
∴DF=BD,AE=AC,
∴DF=AE,
∵AB=AD=DC,点E、F分别是对角线AC、BD的中点,
∴AF⊥BD,DE⊥AC,
在Rt△ADF和Rt△DAE中,
∵,
∴△ADF≌△DAE(HL),
∴∠DAE=∠ADF,AF=DE,
在△AFE和△DEF中,
∵,
∴△AFE≌△DEF(SSS),
∴∠AEF=∠DFE,
设对角线交于点O,
∴∠AOD=180°﹣∠DAE﹣∠ADF=180°﹣2∠DAE,∠EOF=180°﹣∠AEF﹣∠DFE=180°﹣2∠AEF,
∵∠AOD=∠EOF,
∴∠DAE=∠AEF,
∴EF∥AD,
∵AF⊥BD,DE⊥AC,
∴∠DAF和∠ADE都是锐角,
∴AF与DE不平行,
∴ADEF为梯形,
又DF=AE,
∴ADEF为等腰梯形.
