直线与圆的位置关系
图片预览
文档简介
直线与圆的位置关系
教学目标:
1、知识与能力:使学生掌握直线和圆的三种位置关系及其判定方法和性质。
2、过程与方法:通过直线和圆的位置关系的探究,向学生渗透类比、分类、数形结合的思想、算法思想,培养学生观察、分析和发现问题的能力。
3、情感态度价值观:使学生从运动的观点来观察直线和圆相交、相切、相离的关系、培养学生的辩正唯物主义观点。
教学重点:
直线与圆的三种位置关系。
教学难点:
直线与圆的三种位置关系的性质和判定的正确运用。
教学方式:
多媒体教学的运用。
教学过程
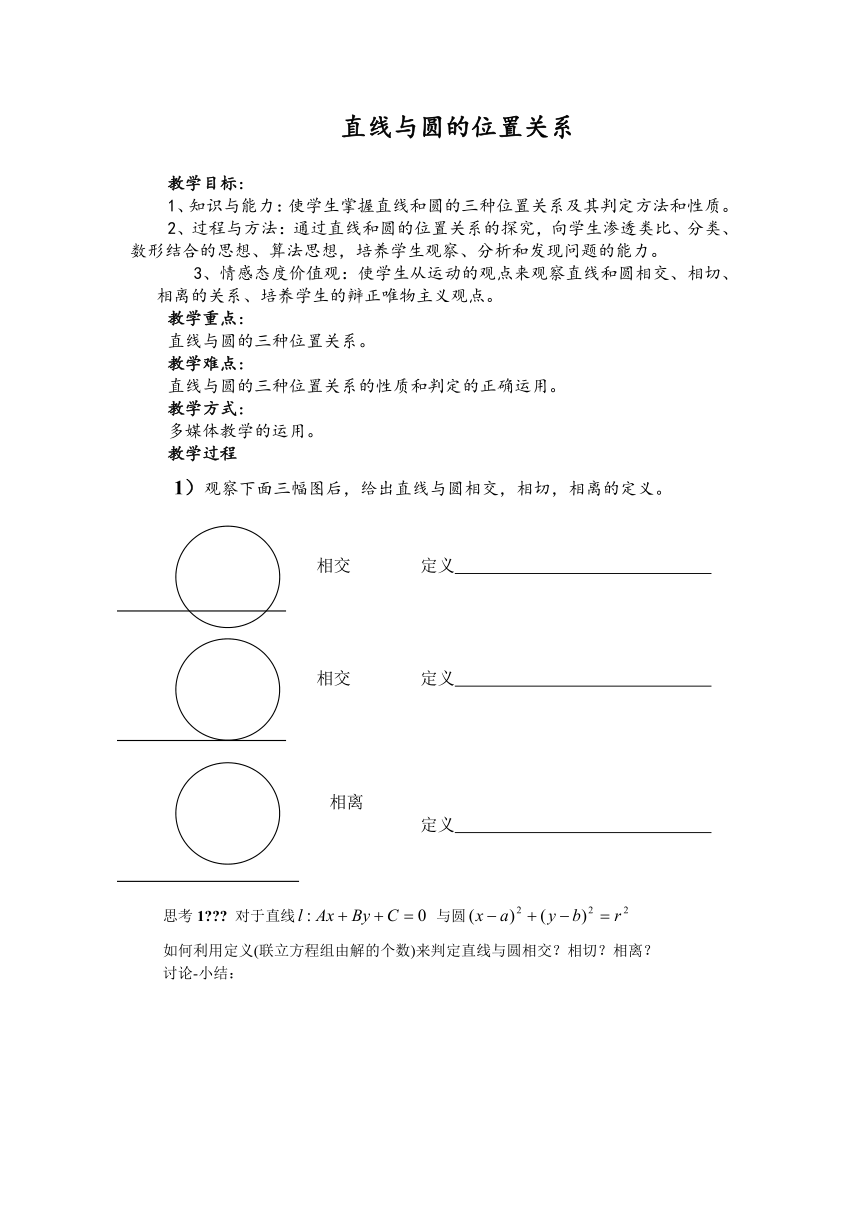
1)观察下面三幅图后,给出直线与圆相交,相切,相离的定义。
思考1 对于直线 与圆
如何利用定义(联立方程组由解的个数)来判定直线与圆相交?相切?相离?
讨论-小结:
2)小试身手
例题1:已知圆C:与直线 判断圆C与直线l的位置关系 ;如果相交,求他们的交点坐标。
例题2已知过点M(-3,-3)的直线被圆x2+y2+4y-21=0所截得的弦长为,求直线的方程:
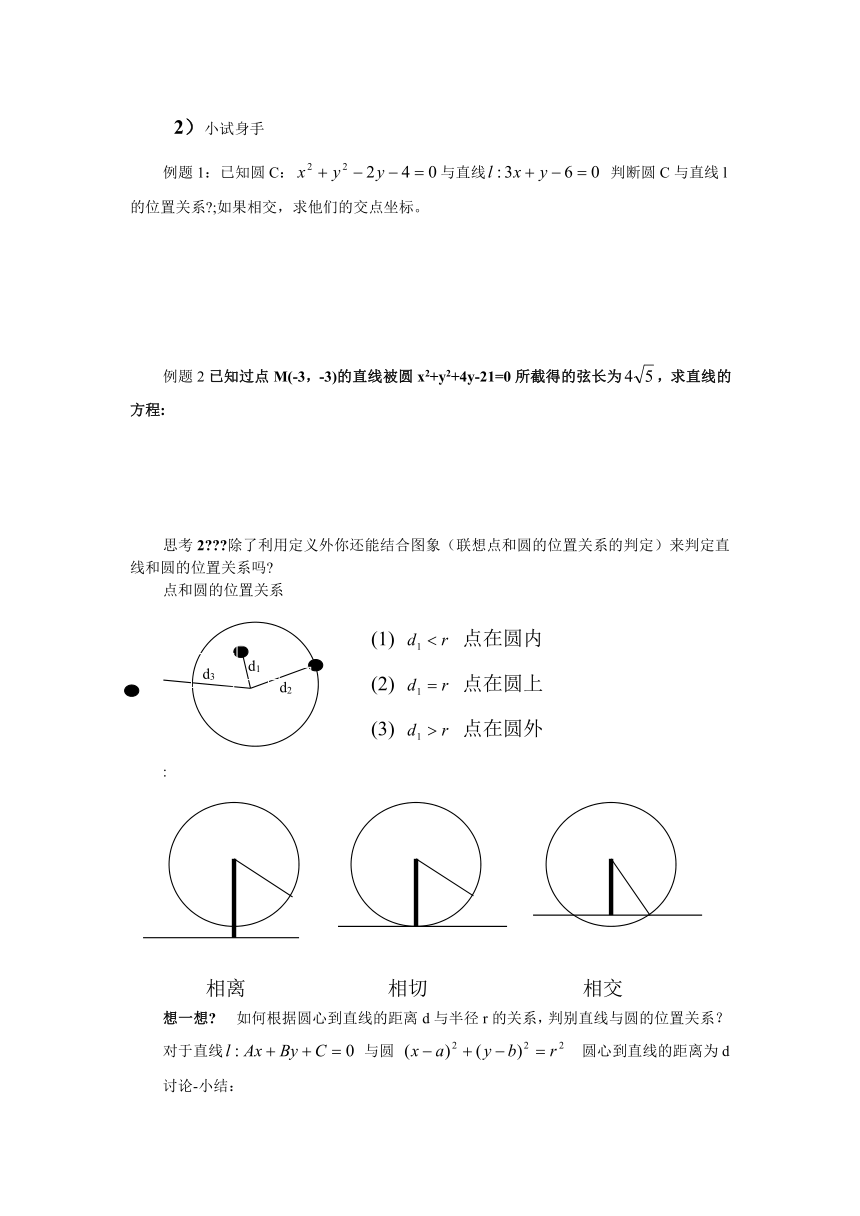
思考2 除了利用定义外你还能结合图象(联想点和圆的位置关系的判定)来判定直线和圆的位置关系吗
点和圆的位置关系
:
想一想 如何根据圆心到直线的距离d与半径r的关系,判别直线与圆的位置关系?
对于直线 与圆 圆心到直线的距离为d
讨论-小结:
3)小试身手
用几何法做上面例题1和例题2
例题1:已知圆C:与直线 判断圆C与直线l的位置关系
例题2:已知过点M(-3,-3)的直线被圆x2+y2+4y-21=0所截得的弦长为,求直线的方程:
4)课堂小结:
1,直线和圆的位置关系有那些 是如何定义的
2,如何用代数法判定直线与圆的位置关系
直线方程L:Ax+By+C=0 圆的方程C:(x-a)2+(y-b)2=r2
步骤:
第一步:联立方程组
第二步 求出
第三步 根据判定直线与圆的位置关系
3,如何用几何法判定直线与圆的位置关系
直线方程L:Ax+By+C=0 圆的方程C:(x-a)2+(y-b)2=r2
步骤
第一步:求出圆心(a,b)到直线Ax+By+C=0的距离d
第二步:比较与的大小
、
5)内容巩固
例3已知圆C: 与直线 当为值时直线与圆C相交 相切 相离
例题4 已知直线与圆相交于两点,求弦长的值
相交
相交
相离
定义
定义
定义
(1) 点在圆内
(2) 点在圆上
(3) 点在圆外
d1
d2
d3
相离
相切
相交
x
y
O
A
B
d
r
教学目标:
1、知识与能力:使学生掌握直线和圆的三种位置关系及其判定方法和性质。
2、过程与方法:通过直线和圆的位置关系的探究,向学生渗透类比、分类、数形结合的思想、算法思想,培养学生观察、分析和发现问题的能力。
3、情感态度价值观:使学生从运动的观点来观察直线和圆相交、相切、相离的关系、培养学生的辩正唯物主义观点。
教学重点:
直线与圆的三种位置关系。
教学难点:
直线与圆的三种位置关系的性质和判定的正确运用。
教学方式:
多媒体教学的运用。
教学过程
1)观察下面三幅图后,给出直线与圆相交,相切,相离的定义。
思考1 对于直线 与圆
如何利用定义(联立方程组由解的个数)来判定直线与圆相交?相切?相离?
讨论-小结:
2)小试身手
例题1:已知圆C:与直线 判断圆C与直线l的位置关系 ;如果相交,求他们的交点坐标。
例题2已知过点M(-3,-3)的直线被圆x2+y2+4y-21=0所截得的弦长为,求直线的方程:
思考2 除了利用定义外你还能结合图象(联想点和圆的位置关系的判定)来判定直线和圆的位置关系吗
点和圆的位置关系
:
想一想 如何根据圆心到直线的距离d与半径r的关系,判别直线与圆的位置关系?
对于直线 与圆 圆心到直线的距离为d
讨论-小结:
3)小试身手
用几何法做上面例题1和例题2
例题1:已知圆C:与直线 判断圆C与直线l的位置关系
例题2:已知过点M(-3,-3)的直线被圆x2+y2+4y-21=0所截得的弦长为,求直线的方程:
4)课堂小结:
1,直线和圆的位置关系有那些 是如何定义的
2,如何用代数法判定直线与圆的位置关系
直线方程L:Ax+By+C=0 圆的方程C:(x-a)2+(y-b)2=r2
步骤:
第一步:联立方程组
第二步 求出
第三步 根据判定直线与圆的位置关系
3,如何用几何法判定直线与圆的位置关系
直线方程L:Ax+By+C=0 圆的方程C:(x-a)2+(y-b)2=r2
步骤
第一步:求出圆心(a,b)到直线Ax+By+C=0的距离d
第二步:比较与的大小
、
5)内容巩固
例3已知圆C: 与直线 当为值时直线与圆C相交 相切 相离
例题4 已知直线与圆相交于两点,求弦长的值
相交
相交
相离
定义
定义
定义
(1) 点在圆内
(2) 点在圆上
(3) 点在圆外
d1
d2
d3
相离
相切
相交
x
y
O
A
B
d
r
