人教版四年级下册数学数学广角鸡兔同笼教案
文档属性
| 名称 | 人教版四年级下册数学数学广角鸡兔同笼教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 18:44:03 | ||
图片预览

文档简介
数学广角
——鸡兔同笼
教学内容:
教材第九单元《数学广角》。
教学目标:
1、了解“鸡兔同笼”问题,尝试用列举法和假设法解决“鸡兔同笼”问题。
2、在解决问题的过程中培养学生的逻辑推理能力,初步理解假设法。
3、感受古代数学问题的趣味性,受到祖国优秀数学文化的熏陶和感染。
教学重点:
用假设法解决“鸡兔同笼”问题。
教学难点:
假设法的理解。
教学过程:
一、创设情境,提出问题
师:我国是一个数学大国,从古至今,产生了许多数学名著和数学趣题。我们先来看一个短片介绍。
(多媒体出示:在我国古代,流传着许多有趣的数学问题,如“韩信点兵”、“三女归家”、“求碗问题”、“三阶幻方”等,这些问题,有的成为经典,有的为世界数学的发展起到了巨大的贡献。“鸡兔同笼”就是其中之一。早在1500年前,数学名著《孙子算经》中就记载了“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”)
师:谁能试着解释一下这道题的意思?(学生解释)对,正如你所说的,这道题的意思就是:
(出示:笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?)
师:有不少的同学在兴趣小组或课外阅读中接触过这类问题,这节课我们继续来研究它。
(板书课题:鸡兔同笼)
二、解决问题,探究新知
(一)明确方法
师:这道题中的数据比较大,我们可以把数据改小,先从简单的问题入手。把35个头改为8个头,把94只脚改为26只脚。
(出示例1:笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?)
师:请大家默读题目,思考一下:从上面数,有8个头是什么意思?从下面数,有26只脚又表示什么?
师:解决这道题都有哪些方法呢?小组内讨论一下。
(学生可能出现的方法有:a.画图法;b.列表法;c.假设法;d.方程解法……教师板书这些方法)
(二)探讨方法
1.画图法
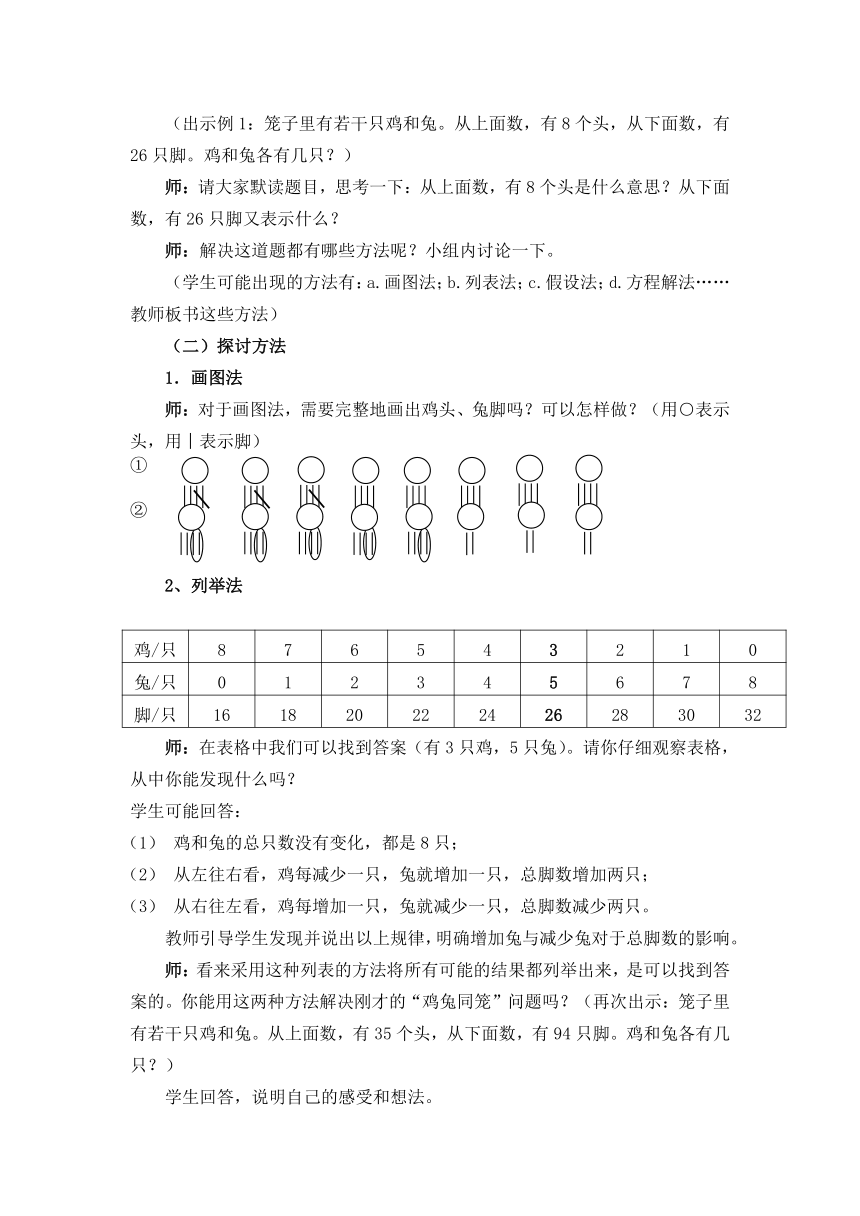
师:对于画图法,需要完整地画出鸡头、兔脚吗?可以怎样做?(用○表示头,用︱表示脚)
①
②
2、列举法
鸡/只
8
7
6
5
4
3
2
1
0
兔/只
0
1
2
3
4
5
6
7
8
脚/只
16
18
20
22
24
26
28
30
32
师:在表格中我们可以找到答案(有3只鸡,5只兔)。请你仔细观察表格,从中你能发现什么吗?
学生可能回答:
鸡和兔的总只数没有变化,都是8只;
从左往右看,鸡每减少一只,兔就增加一只,总脚数增加两只;
从右往左看,鸡每增加一只,兔就减少一只,总脚数减少两只。
教师引导学生发现并说出以上规律,明确增加兔与减少兔对于总脚数的影响。
师:看来采用这种列表的方法将所有可能的结果都列举出来,是可以找到答案的。你能用这两种方法解决刚才的“鸡兔同笼”问题吗?(再次出示:笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?)
学生回答,说明自己的感受和想法。
3、假设法
师:我们来大胆猜测一下这道题的结果吧。老师先猜一个,鸡16只,兔19只,谁也愿意来猜一猜?
(相机板书:鸡16只兔19只;鸡30只,兔5只)
师:老师猜对了吗?怎样来验证?(列式:16×2+19×4=108)
算出来是108只脚,脚多了说明了什么?
如果要你们在这个基础上接着猜,你们会怎样猜呢?
(指2—3名学生回答)为什么你们都减少兔增加鸡呢?
学生回答后,小结:因为一只兔比一只鸡多两只脚,所以脚多了的时候应该减少兔增加鸡。教师引导学生朝着这个方向再猜,(如:鸡20只,兔15只。列式:20×2+15×4=100)脚还是多了,还要减少兔增加鸡。
师:看来,只要找对了方向,像这样继续猜下去,我们也可以找到答案。接下来请大家象刚才这样验证第二组,如果不对,请试着进行调整并找到答案,数一数,你做了几次调整。
(学生活动,教师巡视,参与讨论并及时给予辅导)
指名学生展示自己的猜测过程,教师引导其他学生及时作出评议。
师:刚才老师发现有的同学调整了5次找到答案,有的同学只调整了2次就找出答案了。想一想,能一次就调整出答案吗?
(学生回答,教师引导学生进一步明确增加a只兔,就减少a只鸡,相应的就增加2a只脚;反之,增加a只鸡,就减少a只兔,相应的就减少2a只脚;)
师:多么有智慧的调整啊!这个调整的过程怎样用算式表示呢?
学生思考后,让学生上台板演:
鸡30只,兔5只
30×2+5×4=80(只)
94-80=14(只)
14÷(4-2)=7(只)
30-7=23(只)……鸡
5+7=12(只)……兔
学生列式后,引导其他学生评议并提出问题,明确“4-2”表示什么,求出的“7”又表示什么?教师再将前面的“鸡30只,兔5只”改为“假设鸡有30只,兔有5只”
师:其实,我们也可以首先猜假设鸡是0只,兔是35只,也就是假设笼子里全是兔;或者首先假设鸡35只,兔是0只,也就是假设笼子里全是鸡。请你选择一种,列出算式,解决问题。
指名板书计算过程:
假设笼子里全是鸡。
35×2+0×4=70(只)
(红色表示可以省略的)
94-70=24(只)
24÷(4-2)=12(只)
0+12=12(只)……鸡
35-12=23(只)……兔
师:象这样首先假设一种情况,再根据题目中的条件进行分析调整,直到找出答案的方法就是假设法。比较这两种假设方法,你认为哪种更简便?(学生自由评议)所以在解答类似的问题时,我们一般都采用后面的这种假设情况。
(三)延伸方法
师:刚才我们用自己的方法解决了这道历史名题,那么在《孙子算经》中又是怎样解决这个问题的呢?
(出示:教材第114页的阅读资料。)
师:这道数学历史名题,引起了世界上许多数学家的兴趣。我国著名的数学家张景中院士提出了很奇妙的解法。
出示:假设鸡的两只翅膀也变成两只脚,那么一共有35×4=140(只)脚,这样就多出了140-94=46(只)脚,这多出来的46只脚其实是鸡的翅膀。一只鸡是两只翅膀,所以有46÷2=23(只)鸡,从而求出兔是35-23=12(只)。
师:看来我们在解决问题的时候也需要有点数学家奇思妙想的本领。
建立模型,推广应用
师:“鸡兔同笼”问题后来传到日本,在日本称为“龟鹤算”,题目也发生了变化。
(出示:有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟和鹤各有几只?)
师:日本人说的“龟鹤”和我们说的“鸡兔”有联系吗?看来这类问题不仅可以叫鸡兔同笼问题,也能叫龟鹤问题了。
师:在我们的生活中,类似鸡兔同笼的问题也是很多的,那就让我们带着数学的眼光到生活中去找一找。
(多媒体出示:全班一共有58人,共租了12条船。每条大船坐6人,每条小船坐4人,恰好全都坐满。大小船各租了几条?)
师:这道题还能用“鸡兔同笼”问题的方法来解答吗?为什么?看来,“鸡兔同笼”问题不仅仅是单纯是指鸡和兔的问题了,它是一种模型,因此我们可以给课题加上一个引号。
师:请你任选一题,用今天学到的方法快速的解决它吧。
学生独立完成,教师巡视并进行个别辅导。完成后指名说明解题思路及过程,集体评议。
二、反思交流,结束新课
师:今天我们学习了用列举法和假设法来解决“鸡兔同笼”问题,列方程的方法下节课再学习。通过这节课的学习,你有什么感受呢?你还有什么问题吗?
这节课就上到这里,同学们再见。
板书设计:
鸡兔同笼
假设笼子里全是鸡。
35×2+0×4=70(只)
(红色表示可以省略的)
94-70=24(只)
24÷(4-2)=12(只)
0+12=12(只)……鸡
35-12=23(只)……兔
教学后记:
——鸡兔同笼
教学内容:
教材第九单元《数学广角》。
教学目标:
1、了解“鸡兔同笼”问题,尝试用列举法和假设法解决“鸡兔同笼”问题。
2、在解决问题的过程中培养学生的逻辑推理能力,初步理解假设法。
3、感受古代数学问题的趣味性,受到祖国优秀数学文化的熏陶和感染。
教学重点:
用假设法解决“鸡兔同笼”问题。
教学难点:
假设法的理解。
教学过程:
一、创设情境,提出问题
师:我国是一个数学大国,从古至今,产生了许多数学名著和数学趣题。我们先来看一个短片介绍。
(多媒体出示:在我国古代,流传着许多有趣的数学问题,如“韩信点兵”、“三女归家”、“求碗问题”、“三阶幻方”等,这些问题,有的成为经典,有的为世界数学的发展起到了巨大的贡献。“鸡兔同笼”就是其中之一。早在1500年前,数学名著《孙子算经》中就记载了“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”)
师:谁能试着解释一下这道题的意思?(学生解释)对,正如你所说的,这道题的意思就是:
(出示:笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?)
师:有不少的同学在兴趣小组或课外阅读中接触过这类问题,这节课我们继续来研究它。
(板书课题:鸡兔同笼)
二、解决问题,探究新知
(一)明确方法
师:这道题中的数据比较大,我们可以把数据改小,先从简单的问题入手。把35个头改为8个头,把94只脚改为26只脚。
(出示例1:笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?)
师:请大家默读题目,思考一下:从上面数,有8个头是什么意思?从下面数,有26只脚又表示什么?
师:解决这道题都有哪些方法呢?小组内讨论一下。
(学生可能出现的方法有:a.画图法;b.列表法;c.假设法;d.方程解法……教师板书这些方法)
(二)探讨方法
1.画图法
师:对于画图法,需要完整地画出鸡头、兔脚吗?可以怎样做?(用○表示头,用︱表示脚)
①
②
2、列举法
鸡/只
8
7
6
5
4
3
2
1
0
兔/只
0
1
2
3
4
5
6
7
8
脚/只
16
18
20
22
24
26
28
30
32
师:在表格中我们可以找到答案(有3只鸡,5只兔)。请你仔细观察表格,从中你能发现什么吗?
学生可能回答:
鸡和兔的总只数没有变化,都是8只;
从左往右看,鸡每减少一只,兔就增加一只,总脚数增加两只;
从右往左看,鸡每增加一只,兔就减少一只,总脚数减少两只。
教师引导学生发现并说出以上规律,明确增加兔与减少兔对于总脚数的影响。
师:看来采用这种列表的方法将所有可能的结果都列举出来,是可以找到答案的。你能用这两种方法解决刚才的“鸡兔同笼”问题吗?(再次出示:笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?)
学生回答,说明自己的感受和想法。
3、假设法
师:我们来大胆猜测一下这道题的结果吧。老师先猜一个,鸡16只,兔19只,谁也愿意来猜一猜?
(相机板书:鸡16只兔19只;鸡30只,兔5只)
师:老师猜对了吗?怎样来验证?(列式:16×2+19×4=108)
算出来是108只脚,脚多了说明了什么?
如果要你们在这个基础上接着猜,你们会怎样猜呢?
(指2—3名学生回答)为什么你们都减少兔增加鸡呢?
学生回答后,小结:因为一只兔比一只鸡多两只脚,所以脚多了的时候应该减少兔增加鸡。教师引导学生朝着这个方向再猜,(如:鸡20只,兔15只。列式:20×2+15×4=100)脚还是多了,还要减少兔增加鸡。
师:看来,只要找对了方向,像这样继续猜下去,我们也可以找到答案。接下来请大家象刚才这样验证第二组,如果不对,请试着进行调整并找到答案,数一数,你做了几次调整。
(学生活动,教师巡视,参与讨论并及时给予辅导)
指名学生展示自己的猜测过程,教师引导其他学生及时作出评议。
师:刚才老师发现有的同学调整了5次找到答案,有的同学只调整了2次就找出答案了。想一想,能一次就调整出答案吗?
(学生回答,教师引导学生进一步明确增加a只兔,就减少a只鸡,相应的就增加2a只脚;反之,增加a只鸡,就减少a只兔,相应的就减少2a只脚;)
师:多么有智慧的调整啊!这个调整的过程怎样用算式表示呢?
学生思考后,让学生上台板演:
鸡30只,兔5只
30×2+5×4=80(只)
94-80=14(只)
14÷(4-2)=7(只)
30-7=23(只)……鸡
5+7=12(只)……兔
学生列式后,引导其他学生评议并提出问题,明确“4-2”表示什么,求出的“7”又表示什么?教师再将前面的“鸡30只,兔5只”改为“假设鸡有30只,兔有5只”
师:其实,我们也可以首先猜假设鸡是0只,兔是35只,也就是假设笼子里全是兔;或者首先假设鸡35只,兔是0只,也就是假设笼子里全是鸡。请你选择一种,列出算式,解决问题。
指名板书计算过程:
假设笼子里全是鸡。
35×2+0×4=70(只)
(红色表示可以省略的)
94-70=24(只)
24÷(4-2)=12(只)
0+12=12(只)……鸡
35-12=23(只)……兔
师:象这样首先假设一种情况,再根据题目中的条件进行分析调整,直到找出答案的方法就是假设法。比较这两种假设方法,你认为哪种更简便?(学生自由评议)所以在解答类似的问题时,我们一般都采用后面的这种假设情况。
(三)延伸方法
师:刚才我们用自己的方法解决了这道历史名题,那么在《孙子算经》中又是怎样解决这个问题的呢?
(出示:教材第114页的阅读资料。)
师:这道数学历史名题,引起了世界上许多数学家的兴趣。我国著名的数学家张景中院士提出了很奇妙的解法。
出示:假设鸡的两只翅膀也变成两只脚,那么一共有35×4=140(只)脚,这样就多出了140-94=46(只)脚,这多出来的46只脚其实是鸡的翅膀。一只鸡是两只翅膀,所以有46÷2=23(只)鸡,从而求出兔是35-23=12(只)。
师:看来我们在解决问题的时候也需要有点数学家奇思妙想的本领。
建立模型,推广应用
师:“鸡兔同笼”问题后来传到日本,在日本称为“龟鹤算”,题目也发生了变化。
(出示:有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟和鹤各有几只?)
师:日本人说的“龟鹤”和我们说的“鸡兔”有联系吗?看来这类问题不仅可以叫鸡兔同笼问题,也能叫龟鹤问题了。
师:在我们的生活中,类似鸡兔同笼的问题也是很多的,那就让我们带着数学的眼光到生活中去找一找。
(多媒体出示:全班一共有58人,共租了12条船。每条大船坐6人,每条小船坐4人,恰好全都坐满。大小船各租了几条?)
师:这道题还能用“鸡兔同笼”问题的方法来解答吗?为什么?看来,“鸡兔同笼”问题不仅仅是单纯是指鸡和兔的问题了,它是一种模型,因此我们可以给课题加上一个引号。
师:请你任选一题,用今天学到的方法快速的解决它吧。
学生独立完成,教师巡视并进行个别辅导。完成后指名说明解题思路及过程,集体评议。
二、反思交流,结束新课
师:今天我们学习了用列举法和假设法来解决“鸡兔同笼”问题,列方程的方法下节课再学习。通过这节课的学习,你有什么感受呢?你还有什么问题吗?
这节课就上到这里,同学们再见。
板书设计:
鸡兔同笼
假设笼子里全是鸡。
35×2+0×4=70(只)
(红色表示可以省略的)
94-70=24(只)
24÷(4-2)=12(只)
0+12=12(只)……鸡
35-12=23(只)……兔
教学后记:
