人教八上数学14.1.2幂的乘方 课件(23张ppt)
文档属性
| 名称 | 人教八上数学14.1.2幂的乘方 课件(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
14.1.2
幂的乘方
课件说明
本课是在学生已经学习了同底数幂乘法的性质的基础上,进一步研究幂的乘方与积的乘方这两个幂的运算性质,它们都是后续学习整式乘法的基础.
课件说明
学习目标:
1.理解幂的乘方与积的乘方性质的推导根据.
2.会运用幂的乘方与积的乘方性质进行计算.
3.在类比同底数幂的乘法性质学习幂的乘方与积的
乘方性质时,体会三者的联系和区别及类比、归
纳的思想方法.
学习重点:
幂的乘方与积的乘方的性质.
(1)
(3)
(5)
(6)
(2)
(4)
1.口述同底数幂的乘法法则:
am
·
an
=
am+n
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
2.计算:
温故而知新
3.
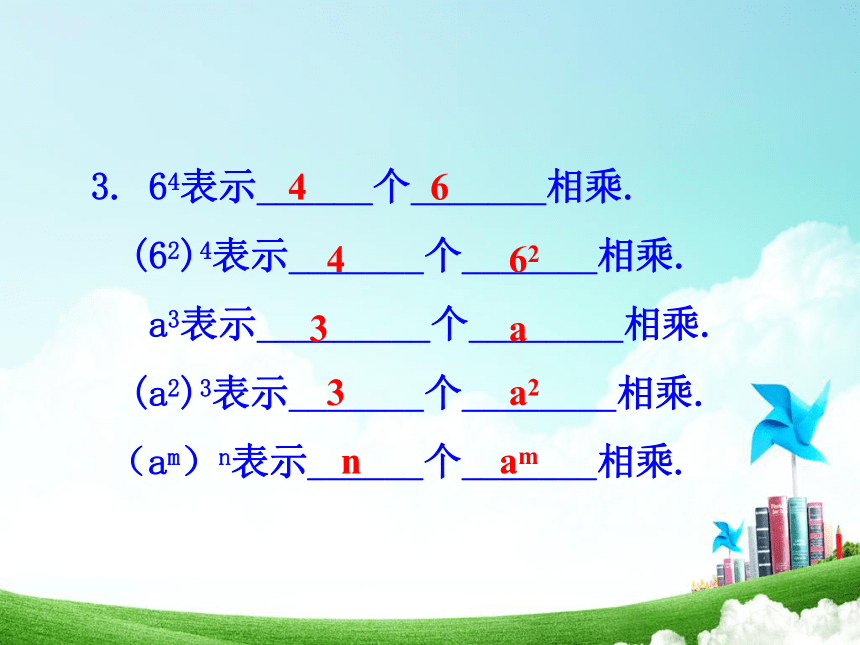
64表示______个_______相乘.
(62)4表示_______个_______相乘.
a3表示_________个________相乘.
(a2)3表示_______个________相乘.
(am)n表示______个_______相乘.
4
6
4
62
3
a
3
a2
n
am
创设情境,导入新知
解:
答:这个铁盒的容积是a6
.
问题1 有一个边长为a2
的正方体铁盒,这个铁盒
的容积是多少?
观察计算结果,你能发现什么规律?
创设情境,导入新知
问题2 根据乘方的意义及同底数幂的乘法填空:
(1)
(2)
(3) (m是正整数).
细心观察,归纳总结
对于任意底数a
与任意正整数m
,n,
?
(
m
,n都是正整数)
多重乘方可以重复运用上述法则:
细心观察,归纳总结
(m
,n
都是正整数).
幂的乘方,底数不变,指数相乘.
幂的乘方性质:
(
m
,n
,p是正整数).
动脑思考,例题解析
解:
(1)
(2)
(3)
(4)
例1 计算:
(1)
(2)
(3)
(4)
动脑思考,变式训练
练习 计算下列各题:
(1)
(2)
(3)
(4)
(5)
(6)
(3)原式=-x5m.(4)原式=a6·a5=a11.
解:(1)原式=109.(2)原式=x6.
(5)原式=x42.
(6)原式=2x2n-x2n=x2n.
动脑思考,例题解析
已知:
,求
的值.
动脑思考,例题解析
已知:
,求
的值.
细心观察,归纳总结
对于幂的乘方公式的逆用:
(
m
,n都是正整数)
动脑思考,变式训练
练习 计算:
(1)
(2)
(3)
(4)
(5)
109
x6
-x5m
a11
16a4b12c8
小结:
今天,我们学到了什么?
幂的乘方的运算性质:
(am)n
=
amn
(
m,n
都是正整数
).
同底数幂乘法的运算性质:
am
·
an=
am+n
(
m,n
都是正整数
)
底数 ,指数 。
不变
相加
底数 ,指数 。
不变
相乘
1.计算-(-3a)2的结果是(
)
A.-6a2
B.-9a2
C.6a2
D.9a2
2.(-2)3
等于(
)
A.-6
B.6
C.-8
D.8
当堂检测
B
C
3.若(x2)m=x8,则m=______.
4.若[(x3)m]2=x12,则m=_______.
5.若xm·x2m=2,求x9m的值.
6.若a3n=3,求(a3n)4的值.
解:xm·x2m=
x3m
=2,
x9m
=(x3m)3
=
23
=8.
解:(a3n)4
=34
=81.
7.已知am=2,an=3,求a2m+3n的值.
【解析】
a2m+3n
=
(am)2
·(an)3
=
22×
33
=4×27
=108.
1.已知,44?83=2x,求x的值.
2.
a=355
,b=444
,c=533
,
比较a、b、c
的大小
谢谢!
14.1.2
幂的乘方
课件说明
本课是在学生已经学习了同底数幂乘法的性质的基础上,进一步研究幂的乘方与积的乘方这两个幂的运算性质,它们都是后续学习整式乘法的基础.
课件说明
学习目标:
1.理解幂的乘方与积的乘方性质的推导根据.
2.会运用幂的乘方与积的乘方性质进行计算.
3.在类比同底数幂的乘法性质学习幂的乘方与积的
乘方性质时,体会三者的联系和区别及类比、归
纳的思想方法.
学习重点:
幂的乘方与积的乘方的性质.
(1)
(3)
(5)
(6)
(2)
(4)
1.口述同底数幂的乘法法则:
am
·
an
=
am+n
(m,n都是正整数).
同底数幂相乘,底数不变,指数相加.
2.计算:
温故而知新
3.
64表示______个_______相乘.
(62)4表示_______个_______相乘.
a3表示_________个________相乘.
(a2)3表示_______个________相乘.
(am)n表示______个_______相乘.
4
6
4
62
3
a
3
a2
n
am
创设情境,导入新知
解:
答:这个铁盒的容积是a6
.
问题1 有一个边长为a2
的正方体铁盒,这个铁盒
的容积是多少?
观察计算结果,你能发现什么规律?
创设情境,导入新知
问题2 根据乘方的意义及同底数幂的乘法填空:
(1)
(2)
(3) (m是正整数).
细心观察,归纳总结
对于任意底数a
与任意正整数m
,n,
?
(
m
,n都是正整数)
多重乘方可以重复运用上述法则:
细心观察,归纳总结
(m
,n
都是正整数).
幂的乘方,底数不变,指数相乘.
幂的乘方性质:
(
m
,n
,p是正整数).
动脑思考,例题解析
解:
(1)
(2)
(3)
(4)
例1 计算:
(1)
(2)
(3)
(4)
动脑思考,变式训练
练习 计算下列各题:
(1)
(2)
(3)
(4)
(5)
(6)
(3)原式=-x5m.(4)原式=a6·a5=a11.
解:(1)原式=109.(2)原式=x6.
(5)原式=x42.
(6)原式=2x2n-x2n=x2n.
动脑思考,例题解析
已知:
,求
的值.
动脑思考,例题解析
已知:
,求
的值.
细心观察,归纳总结
对于幂的乘方公式的逆用:
(
m
,n都是正整数)
动脑思考,变式训练
练习 计算:
(1)
(2)
(3)
(4)
(5)
109
x6
-x5m
a11
16a4b12c8
小结:
今天,我们学到了什么?
幂的乘方的运算性质:
(am)n
=
amn
(
m,n
都是正整数
).
同底数幂乘法的运算性质:
am
·
an=
am+n
(
m,n
都是正整数
)
底数 ,指数 。
不变
相加
底数 ,指数 。
不变
相乘
1.计算-(-3a)2的结果是(
)
A.-6a2
B.-9a2
C.6a2
D.9a2
2.(-2)3
等于(
)
A.-6
B.6
C.-8
D.8
当堂检测
B
C
3.若(x2)m=x8,则m=______.
4.若[(x3)m]2=x12,则m=_______.
5.若xm·x2m=2,求x9m的值.
6.若a3n=3,求(a3n)4的值.
解:xm·x2m=
x3m
=2,
x9m
=(x3m)3
=
23
=8.
解:(a3n)4
=34
=81.
7.已知am=2,an=3,求a2m+3n的值.
【解析】
a2m+3n
=
(am)2
·(an)3
=
22×
33
=4×27
=108.
1.已知,44?83=2x,求x的值.
2.
a=355
,b=444
,c=533
,
比较a、b、c
的大小
谢谢!
