鲁科版(2019)高中物理 选择性必修第三册 第1章 拓展课 气体实验定律和理想气体状态方程的应用word含解析
文档属性
| 名称 | 鲁科版(2019)高中物理 选择性必修第三册 第1章 拓展课 气体实验定律和理想气体状态方程的应用word含解析 |  | |
| 格式 | doc | ||
| 文件大小 | 535.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-11 09:52:40 | ||
图片预览



文档简介
拓展课 气体实验定律和理想气体状态方程的应用
核心要点 理想气体状态方程
[要点归纳]
1.理想气体状态方程的推导
(1)由玻意耳定律可知,一定质量的理想气体,在温度不变时,压强与体积成反比,即p∝。
(2)由查理定律可知,一定质量的理想气体,在体积不变时,压强与热力学温度成正比,即p∝T。
(3)综合以上结论可得,p=C,即=C或=。
2.对理想气体状态方程的理解
(1)成立条件:一定质量的理想气体。
(2)该方程表示的是气体三个状态参量的关系,与中间的变化过程无关。
(3)公式中常量C仅由气体的种类和质量决定,与状态参量(p、V、T)无关。
(4)方程应用时各量的单位:温度T必须是热力学温度,公式两边中压强p和体积V单位必须统一,但不一定是国际单位制中的单位。
3.理想气体状态方程与气体实验定律
=?
[经典示例]
[例1] 如图所示,粗细均匀一端封闭一端开口的U形玻璃管竖直放置,管内水银将一定质量的理想气体封闭在U形管内,当t1=31 ℃,大气压强p0=76 cmHg时,两管水银面相平,这时左管被封闭的气柱长L1=8 cm,则当温度t2是多少时,左管气柱L2为9 cm?
解析 设玻璃管的横截面积为S,
初状态:p1=p0=76 cmHg,
V1=L1·S=8 cm·S,T1=304 K;
末状态:p2=p0+2 cmHg=78 cmHg,
V2=L2·S=9 cm·S,
根据理想气体状态方程=
代入数据解得:T2=351 K,则t2=(351-273) ℃=78 ℃。
答案 78 ℃
规律总结 理想气体状态方程的应用要点
(1)选对象:根据题意,选出所研究的某一部分气体,这部分气体在状态变化过程中,其质量必须保持一定。
(2)找参量:找出作为研究对象的这部分气体发生状态变化前后的一组p、V、T数值或表达式,压强的确定往往是个关键,常需结合力学知识(如力的平衡条件或牛顿运动定律)才能写出表达式。
(3)认过程:过程表示两个状态之间的一种变化式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定,认清变化过程是正确选用物理规律的前提。
(4)列方程:根据研究对象状态变化的具体方式,选用理想气体状态方程或某一实验定律,代入具体数值,T必须用热力学温度,p、V的单位要统一,最后分析讨论所得结果的合理性及其物理意义。
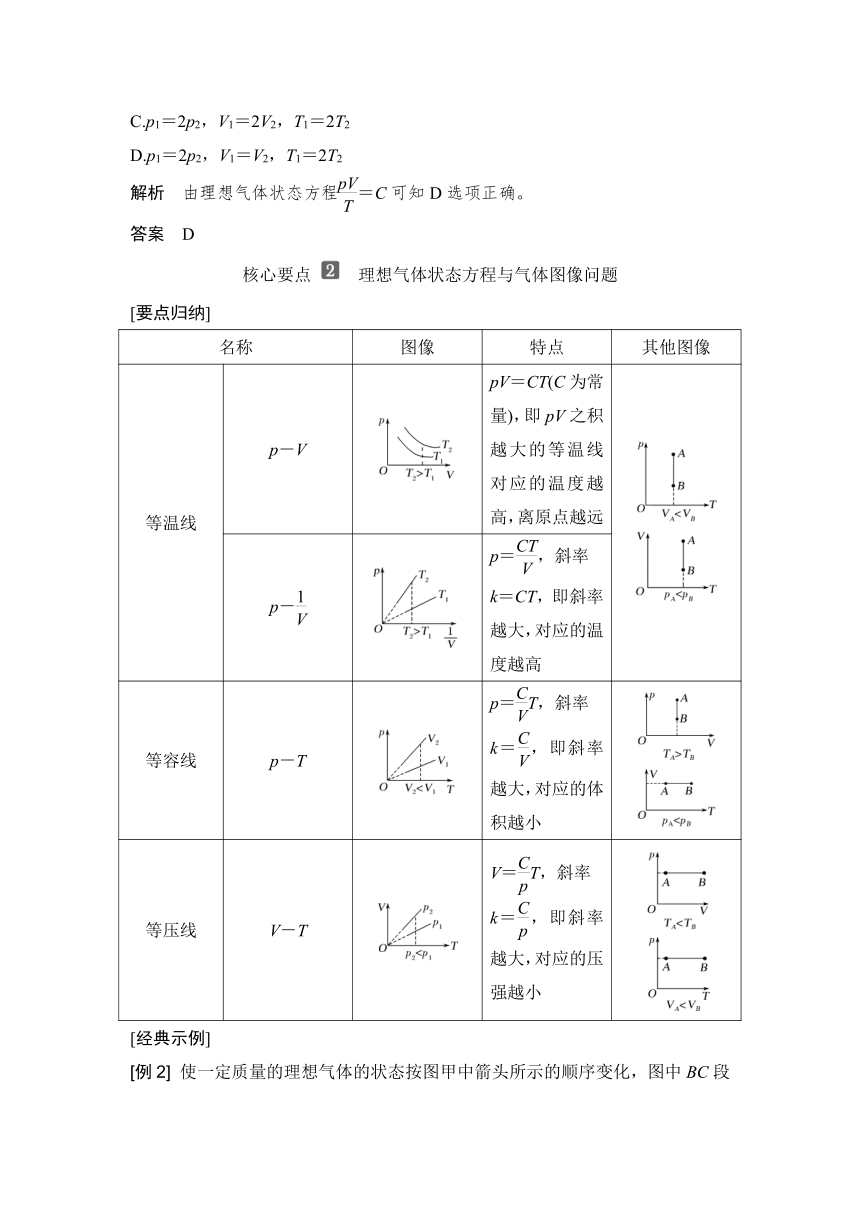
[针对训练1] 一定质量的理想气体,在某一平衡状态下的压强、体积和温度分别为p1、V1、T1,在另一平衡状态下的压强、体积和温度分别为p2、V2、T2,下列关系中可能正确的是( )
A.p1=p2,V1=2V2,T1=T2
B.p1=p2,V1=V2,T1=2T2
C.p1=2p2,V1=2V2,T1=2T2
D.p1=2p2,V1=V2,T1=2T2
解析 由理想气体状态方程=C可知D选项正确。
答案 D
核心要点 理想气体状态方程与气体图像问题
[要点归纳]
名称 图像 特点 其他图像
等温线 p-V
pV=CT(C为常量),即pV之积越大的等温线对应的温度越高,离原点越远
p-
p=,斜率
k=CT,即斜率越大,对应的温度越高
等容线 p-T
p=T,斜率
k=,即斜率越大,对应的体积越小
等压线 V-T
V=T,斜率
k=,即斜率越大,对应的压强越小
[经典示例]
[例2] 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
解析 从p-V图中可以直观地看出,气体在A、B、C、D各状态下压强和体积分别为pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,VA=10 L,VC=40 L,VD=20 L。
(1)根据理想气体状态方程
==,
可得TC=·TA=×300 K=600 K,
TD=·TA=×300 K=300 K,
由题意知B到C是等温变化,所以TB=TC=600 K。
(2)由状态B到状态C为等温变化,
由玻意耳定律有pBVB=pCVC,得
VB== L=20 L。
在V-T图上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
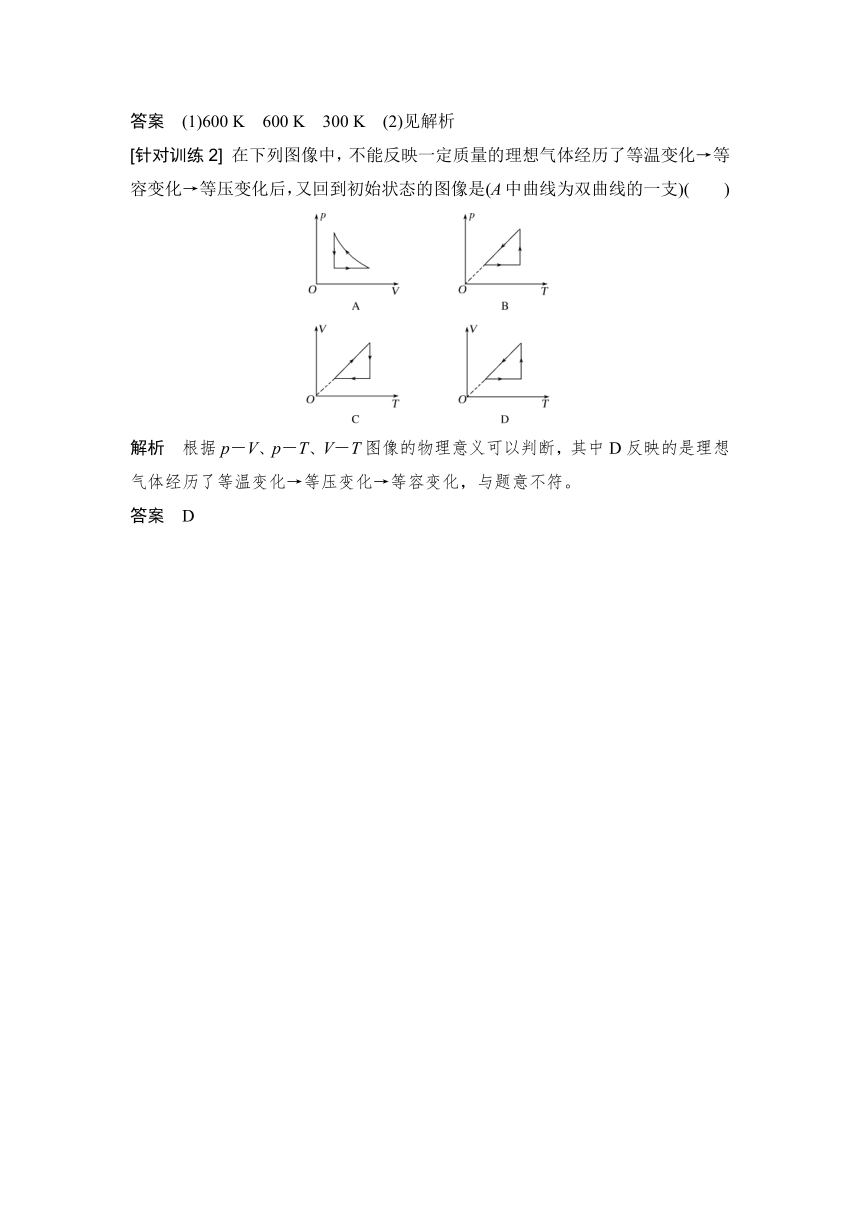
答案 (1)600 K 600 K 300 K (2)见解析
[针对训练2] 在下列图像中,不能反映一定质量的理想气体经历了等温变化→等容变化→等压变化后,又回到初始状态的图像是(A中曲线为双曲线的一支)( )
解析 根据p-V、p-T、V-T图像的物理意义可以判断,其中D反映的是理想气体经历了等温变化→等压变化→等容变化,与题意不符。
答案 D
1.(理想气体状态方程的应用)(多选)一定质量的理想气体,初始状态为p、V、T。经过一系列状态变化后,压强仍为p,则这一系列状态变化可能为( )
A.先等温膨胀,再等容降温
B.先等温压缩,再等容降温
C.先等容升温,再等温压缩
D.先等容降温,再等温压缩
解析 质量一定的理想气体状态无论怎样变化,其的值都不改变。T不变,V增大,则压强p减小,之后V不变,T降低,则压强p减小,压强降了再降,不可能回到初始状态,A项不可能;T不变,V减小,则压强p增大,之后V不变,T降低,则压强p减小,压强先增后减,可能会回到初始状态,即B项可能;V不变,T升高,则压强p增大,之后T不变,V减小,则压强p增大,压强增了再增,末态压强必大于初始状态,C项不可能;V不变,T降低,则p减小,之后T不变,V减小,则压强p增大,压强先减后增,末状态压强可能等于初始状态,D项可能。
答案 BD
2.(理想气体状态方程的应用)一定质量的理想气体,经历了如图所示的状态变化过程,1、2、3为三个状态对应的点,则此三个状态的温度之比是( )
A.1∶3∶5 B.3∶6∶5
C.3∶2∶1 D.5∶6∶3
解析 由理想气体状态方程得:=C(C为常数),可见pV=TC,即pV的乘积与温度T成正比,故B项正确。
答案 B
3.(图像问题)如图所示是理想气体经历的两个状态变化的p-T图像,对应的
p-V图像应是下图中的( )
解析 由图像可知,气体从A到B的过程中做等容变化,从B到C的过程中做等温变化,与之对应的为C选项。
答案 C
4.(气体实验定律与理想气体状态方程的综合应用)如图甲所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2×10-3 m2、质量为m=4 kg、厚度不计的活塞与气缸底部之间封闭了一部分理想气体,此时活塞与气缸底部之间的距离为24 cm,在活塞的右侧12 cm处有一对与气缸固定连接的卡环,气体的温度为300 K,大气压强p0=1×105 Pa。现将气缸竖直放置,如图乙所示,取g=10 m/s2。求:
(1)活塞与气缸底部之间的距离;
(2)加热到675 K时封闭气体的压强。
解析 (1)以气缸内气体为研究对象,
初状态:p1=p0=1×105 Pa
T1=300 K,V1=24 cm×S
末状态:p2=p0+=1.2×105 Pa
T1=T2,V2=HS
由玻意耳定律得p1V1=p2V2
解得H=20 cm。
(2)假设活塞能到达卡环处,则
T3=675 K,V3=36 cm×S
由理想气体状态方程=
得p3=1.5×105 Pa>p2=1.2×105 Pa
所以活塞能到达卡环处,封闭气体压强为1.5×105 Pa。
答案 (1)20 cm (2)1.5×105 Pa
基础过关
1.对于一定质量的理想气体,下列状态变化中可能实现的是( )
A.使气体体积增加而同时温度降低
B.使气体温度升高,体积不变、压强减小
C.使气体温度不变,而压强、体积同时增大
D.使气体温度升高,压强减小,体积减小
解析 由理想气体状态方程=C得A项中只要压强减小就有可能,故A项正确;而B项中体积不变,温度与压强应同时变大或同时变小,故B项错误;C项中温度不变,压强与体积成反比,故不能同时增大,故C项错误;D项中温度升高,压强减小,体积减小,导致减小,故D项错误。
答案 A
2.关于气体的状态变化,下列说法中正确的是( )
A.一定质量的理想气体,当压强不变而温度由100 ℃上升到200 ℃时,其体积增大为原来的2倍
B.一定质量的实际气体由状态1变化到状态2时,一定满足方程=
C.一定质量的理想气体体积增大到原来的4倍,则气体可能压强减半,热力学温度加倍
D.一定质量的理想气体压强增大到原来的4倍,则气体可能体积加倍,热力学温度减半
解析 一定质量的理想气体压强不变,体积与热力学温度成正比,温度由100 ℃上升到200 ℃时,即从373 K上升到473 K,体积增大为原来的1.27倍,故A错误;理想气体状态方程成立的条件为气体可看作理想气体且质量不变,故B错误;由理想气体状态方程=C可知,C正确,D错误。
答案 C
3.如图为伽利略设计的一种测温装置示意图,玻璃管的上端与导热良好的玻璃泡连通,下端插入水中,玻璃泡中封闭有一定质量的空气。若玻璃管中水柱上升,则外界大气的变化可能是( )
A.温度降低,压强增大
B.温度升高,压强不变
C.温度升高,压强减小
D.温度不变,压强减小
解析 由题意可知,玻璃泡中空气温度与大气温度相同,玻璃泡中空气体积随水柱的上升而减小。将玻璃泡中气体近似看成理想气体,根据理想气体状态方程=C,C为恒量,若温度降低,体积减小,压强可能增大、不变或减小,A正确;若温度升高,体积减小,压强一定增大,B、C错误;若温度不变,体积减小,压强一定增大,D错误。
答案 A
4.如图所示,为质量恒定的某种气体的p-T图像,A、B、C三态中体积最大的状态是( )
A.A状态 B.B状态
C.C状态 D.条件不足,无法确定
解析 由理想气体的状态方程=C变形后可得p=T,可见,图线斜率越小时体积越大,C正确。
答案 C
5.已知湖水深度为20 m,湖底水温为 4 ℃,水面温度为17 ℃,大气压强为1.0×105 Pa。当一气泡从湖底缓慢升到水面时,其体积约为原来的(g取10 m/s2,ρ水=1.0×103 kg/m3)( )
A.12.8倍 B.8.5倍
C.3.1倍 D.2.1倍
解析 p1=p0+ρgh=3.0×105 Pa,T0=4 K+273 K=277 K,T1=17 K+273 K=290 K,由=,解得≈3.1,C正确。
答案 C
6.(多选)一定质量的理想气体经历如图所示的一系列过程,ab、bc、cd和da这四个过程在p-T图上都是直线段,ab和dc的延长线通过坐标原点O,bc垂直于ab,ad平行于纵轴,由图可以判断( )
A.ab过程中气体体积不断减小
B.bc过程中气体体积不断减小
C.cd过程中气体体积不断增大
D.da过程中气体体积不断增大
解析 由p-T图线的特点可知a、b在同一条等容线上,体积不变,A错误;c、d在同一条等容线上,体积不变,C错误;在p-T图线中,图线的斜率越大与之对应的体积越小,因此b→c的过程体积减小,同理d→a的过程体积增大,B、D正确。
答案 BD
7.如图所示,圆柱形气缸A中用质量为2m的活塞封闭了一定质量的理想气体,气体温度为27 ℃,气缸中的活塞通过滑轮系统悬挂一质量为m的重物,稳定时活塞与气缸底部的距离为h,现在重物m上加挂一个质量为的小物体,已知大气压强为p0,活塞横截面积为S,m=,g为重力加速度,不计一切摩擦,求当气体温度升高到37 ℃且系统重新稳定后,重物m下降的高度。
解析 以气缸内的气体为研究对象,
初状态时,对活塞,由平衡条件得
p1S+mg=p0S+2mg,
气体压强p1=2p0,气体体积V1=hS,温度T1=300 K
末状态时,对活塞,由平衡条件得
p2S+mg=p0S+2mg
气体压强p2=p0,气体体积V2=(h+Δh)S,温度T2=310 K
根据理想气体状态方程:=
解得Δh=0.24h。
答案 0.24h
能力提升
8.(多选)一定质量理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则气体体积在( )
A.ab过程中不断增大
B.bc过程中保持不变
C.cd过程中不断增大
D.da过程中保持不变
解析 首先,因为bc的延长线通过原点,所以bc是等容线,即气体体积在bc过程中保持不变,B正确;ab是等温线,压强减小则体积增大,A正确;cd是等压线,温度降低则体积减小,C错误;连接aO交cd于e,如图所示,则ae是等容线,即Va=Ve,因为Vd<Ve,所以Vd<Va,da过程中体积不是保持不变,D错误。
答案 AB
9.光滑绝热的轻质活塞把密封的圆筒容器分成A、B两部分,这两部分充有温度相同的理想气体,平衡时VA∶VB=1∶2,现将A中气体加热到127 ℃,B中气体降低到27 ℃,待重新平衡后,这两部分气体体积的比VA′∶VB′为( )
A.1∶1 B.2∶3
C.3∶4 D.2∶1
解析 对A部分气体有:=①
对B部分气体有:=②
因为pA=pB,pA′=pB′,TA=TB,
所以将①÷②式得=
所以===。
答案 B
10.如图所示,一定质量的气体从状态A经状态B、C、D再回到状态A。问AB、BC、CD、DA是什么过程?已知气体在状态A时的体积是1 L,则在状态B、C、D时的体积各为多少?并把此图改为p-V图。
解析 AB过程是等容升温升压过程,BC过程是等压膨胀过程,CD过程是等温膨胀过程,DA过程是等压压缩过程。
现求A、B、C、D各点的体积:已知VA=1 L,VB=1 L(等容过程),
由=(等压过程),
得VC=TC=900× L=2 L;
由pDVD=pCVC(等温过程),
得VD=VC=2× L=6 L。
改画为p-V图如图所示。
答案 见解析
11.一水银气压计中混进了空气,因而在外界温度为27 ℃、大气压为758 mmHg时,这个水银气压计的读数为738 mmHg,此时管中水银面距管顶80 mm,当温度降至-3 ℃时,这个气压计的读数为743 mmHg,求此时外界的实际大气压值为多少mmHg?
解析 画出该题初、末状态的示意图:
分别写出水银气压计中气体的初、末状态的状态参量:
p1=758 mmHg-738 mmHg=20 mmHg
V1=(80 mm)·S
T1=(273+27) K=300 K
p2=p-743 mmHg
V2=(738+80)mm·S-(743 mm)·S=(75 mm)·S
T2=(273-3) K=270 K
由理想气体状态方程:
=
解得p=762.2 mmHg。
答案 762.2 mmHg
12.如图所示,一固定的竖直气缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞。已知大活塞的质量为m1=2.50 kg,横截面积为S1=80.0 cm2;小活塞的质量为m2=1.50 kg,横截面积为S2=40.0 cm2;两活塞用刚性轻杆连接,间距保持为l=40.0 cm;气缸外大气的压强为p=1.00×105 Pa,温度为T=303 K。初始时大活塞与大圆筒底部相距,两活塞间封闭气体的温度为T1=495 K。现气缸内气体温度缓慢下降,活塞缓慢下移。忽略两活塞与气缸壁之间的摩擦,重力加速度大小g取 10 m/s2。求:
(1)在大活塞与大圆筒底部接触前的瞬间,缸内封闭气体的温度;
(2)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强。
解析 (1)大、小活塞在缓慢下移过程中,受力情况不变,气缸内气体压强不变,由盖—吕萨克定律得=
初状态V1=(S1+S2),T1=495 K
末状态V2=lS2
解得T2=T1=330 K
(2)在大活塞与大圆筒底部接触前的瞬间,对大、小活塞受力分析则有
m1g+m2g+pS1+p1S2=p1S1+pS2
解得p1=1.1×105 Pa
缸内封闭的气体与缸外大气达到热平衡过程中,气体体积不变,由查理定律得
=
T3=T=303 K
解得p2=1.01×105 Pa。
答案 (1)330 K (2)1.01×105 Pa
核心要点 理想气体状态方程
[要点归纳]
1.理想气体状态方程的推导
(1)由玻意耳定律可知,一定质量的理想气体,在温度不变时,压强与体积成反比,即p∝。
(2)由查理定律可知,一定质量的理想气体,在体积不变时,压强与热力学温度成正比,即p∝T。
(3)综合以上结论可得,p=C,即=C或=。
2.对理想气体状态方程的理解
(1)成立条件:一定质量的理想气体。
(2)该方程表示的是气体三个状态参量的关系,与中间的变化过程无关。
(3)公式中常量C仅由气体的种类和质量决定,与状态参量(p、V、T)无关。
(4)方程应用时各量的单位:温度T必须是热力学温度,公式两边中压强p和体积V单位必须统一,但不一定是国际单位制中的单位。
3.理想气体状态方程与气体实验定律
=?
[经典示例]
[例1] 如图所示,粗细均匀一端封闭一端开口的U形玻璃管竖直放置,管内水银将一定质量的理想气体封闭在U形管内,当t1=31 ℃,大气压强p0=76 cmHg时,两管水银面相平,这时左管被封闭的气柱长L1=8 cm,则当温度t2是多少时,左管气柱L2为9 cm?
解析 设玻璃管的横截面积为S,
初状态:p1=p0=76 cmHg,
V1=L1·S=8 cm·S,T1=304 K;
末状态:p2=p0+2 cmHg=78 cmHg,
V2=L2·S=9 cm·S,
根据理想气体状态方程=
代入数据解得:T2=351 K,则t2=(351-273) ℃=78 ℃。
答案 78 ℃
规律总结 理想气体状态方程的应用要点
(1)选对象:根据题意,选出所研究的某一部分气体,这部分气体在状态变化过程中,其质量必须保持一定。
(2)找参量:找出作为研究对象的这部分气体发生状态变化前后的一组p、V、T数值或表达式,压强的确定往往是个关键,常需结合力学知识(如力的平衡条件或牛顿运动定律)才能写出表达式。
(3)认过程:过程表示两个状态之间的一种变化式,除题中条件已直接指明外,在许多情况下,往往需要通过对研究对象跟周围环境的相互关系的分析中才能确定,认清变化过程是正确选用物理规律的前提。
(4)列方程:根据研究对象状态变化的具体方式,选用理想气体状态方程或某一实验定律,代入具体数值,T必须用热力学温度,p、V的单位要统一,最后分析讨论所得结果的合理性及其物理意义。
[针对训练1] 一定质量的理想气体,在某一平衡状态下的压强、体积和温度分别为p1、V1、T1,在另一平衡状态下的压强、体积和温度分别为p2、V2、T2,下列关系中可能正确的是( )
A.p1=p2,V1=2V2,T1=T2
B.p1=p2,V1=V2,T1=2T2
C.p1=2p2,V1=2V2,T1=2T2
D.p1=2p2,V1=V2,T1=2T2
解析 由理想气体状态方程=C可知D选项正确。
答案 D
核心要点 理想气体状态方程与气体图像问题
[要点归纳]
名称 图像 特点 其他图像
等温线 p-V
pV=CT(C为常量),即pV之积越大的等温线对应的温度越高,离原点越远
p-
p=,斜率
k=CT,即斜率越大,对应的温度越高
等容线 p-T
p=T,斜率
k=,即斜率越大,对应的体积越小
等压线 V-T
V=T,斜率
k=,即斜率越大,对应的压强越小
[经典示例]
[例2] 使一定质量的理想气体的状态按图甲中箭头所示的顺序变化,图中BC段是以纵轴和横轴为渐近线的双曲线的一部分。
(1)已知气体在状态A的温度TA=300 K,求气体在状态B、C和D的温度各是多少?
(2)将上述状态变化过程在图乙中画成用体积V和热力学温度T表示的图线(图中要标明A、B、C、D四点,并且要画箭头表示变化的方向),说明每段图线各表示什么过程。
解析 从p-V图中可以直观地看出,气体在A、B、C、D各状态下压强和体积分别为pA=4 atm,pB=4 atm,pC=2 atm,pD=2 atm,VA=10 L,VC=40 L,VD=20 L。
(1)根据理想气体状态方程
==,
可得TC=·TA=×300 K=600 K,
TD=·TA=×300 K=300 K,
由题意知B到C是等温变化,所以TB=TC=600 K。
(2)由状态B到状态C为等温变化,
由玻意耳定律有pBVB=pCVC,得
VB== L=20 L。
在V-T图上状态变化过程的图线由A、B、C、D各状态依次连接(如图),AB是等压膨胀过程,BC是等温膨胀过程,CD是等压压缩过程。
答案 (1)600 K 600 K 300 K (2)见解析
[针对训练2] 在下列图像中,不能反映一定质量的理想气体经历了等温变化→等容变化→等压变化后,又回到初始状态的图像是(A中曲线为双曲线的一支)( )
解析 根据p-V、p-T、V-T图像的物理意义可以判断,其中D反映的是理想气体经历了等温变化→等压变化→等容变化,与题意不符。
答案 D
1.(理想气体状态方程的应用)(多选)一定质量的理想气体,初始状态为p、V、T。经过一系列状态变化后,压强仍为p,则这一系列状态变化可能为( )
A.先等温膨胀,再等容降温
B.先等温压缩,再等容降温
C.先等容升温,再等温压缩
D.先等容降温,再等温压缩
解析 质量一定的理想气体状态无论怎样变化,其的值都不改变。T不变,V增大,则压强p减小,之后V不变,T降低,则压强p减小,压强降了再降,不可能回到初始状态,A项不可能;T不变,V减小,则压强p增大,之后V不变,T降低,则压强p减小,压强先增后减,可能会回到初始状态,即B项可能;V不变,T升高,则压强p增大,之后T不变,V减小,则压强p增大,压强增了再增,末态压强必大于初始状态,C项不可能;V不变,T降低,则p减小,之后T不变,V减小,则压强p增大,压强先减后增,末状态压强可能等于初始状态,D项可能。
答案 BD
2.(理想气体状态方程的应用)一定质量的理想气体,经历了如图所示的状态变化过程,1、2、3为三个状态对应的点,则此三个状态的温度之比是( )
A.1∶3∶5 B.3∶6∶5
C.3∶2∶1 D.5∶6∶3
解析 由理想气体状态方程得:=C(C为常数),可见pV=TC,即pV的乘积与温度T成正比,故B项正确。
答案 B
3.(图像问题)如图所示是理想气体经历的两个状态变化的p-T图像,对应的
p-V图像应是下图中的( )
解析 由图像可知,气体从A到B的过程中做等容变化,从B到C的过程中做等温变化,与之对应的为C选项。
答案 C
4.(气体实验定律与理想气体状态方程的综合应用)如图甲所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2×10-3 m2、质量为m=4 kg、厚度不计的活塞与气缸底部之间封闭了一部分理想气体,此时活塞与气缸底部之间的距离为24 cm,在活塞的右侧12 cm处有一对与气缸固定连接的卡环,气体的温度为300 K,大气压强p0=1×105 Pa。现将气缸竖直放置,如图乙所示,取g=10 m/s2。求:
(1)活塞与气缸底部之间的距离;
(2)加热到675 K时封闭气体的压强。
解析 (1)以气缸内气体为研究对象,
初状态:p1=p0=1×105 Pa
T1=300 K,V1=24 cm×S
末状态:p2=p0+=1.2×105 Pa
T1=T2,V2=HS
由玻意耳定律得p1V1=p2V2
解得H=20 cm。
(2)假设活塞能到达卡环处,则
T3=675 K,V3=36 cm×S
由理想气体状态方程=
得p3=1.5×105 Pa>p2=1.2×105 Pa
所以活塞能到达卡环处,封闭气体压强为1.5×105 Pa。
答案 (1)20 cm (2)1.5×105 Pa
基础过关
1.对于一定质量的理想气体,下列状态变化中可能实现的是( )
A.使气体体积增加而同时温度降低
B.使气体温度升高,体积不变、压强减小
C.使气体温度不变,而压强、体积同时增大
D.使气体温度升高,压强减小,体积减小
解析 由理想气体状态方程=C得A项中只要压强减小就有可能,故A项正确;而B项中体积不变,温度与压强应同时变大或同时变小,故B项错误;C项中温度不变,压强与体积成反比,故不能同时增大,故C项错误;D项中温度升高,压强减小,体积减小,导致减小,故D项错误。
答案 A
2.关于气体的状态变化,下列说法中正确的是( )
A.一定质量的理想气体,当压强不变而温度由100 ℃上升到200 ℃时,其体积增大为原来的2倍
B.一定质量的实际气体由状态1变化到状态2时,一定满足方程=
C.一定质量的理想气体体积增大到原来的4倍,则气体可能压强减半,热力学温度加倍
D.一定质量的理想气体压强增大到原来的4倍,则气体可能体积加倍,热力学温度减半
解析 一定质量的理想气体压强不变,体积与热力学温度成正比,温度由100 ℃上升到200 ℃时,即从373 K上升到473 K,体积增大为原来的1.27倍,故A错误;理想气体状态方程成立的条件为气体可看作理想气体且质量不变,故B错误;由理想气体状态方程=C可知,C正确,D错误。
答案 C
3.如图为伽利略设计的一种测温装置示意图,玻璃管的上端与导热良好的玻璃泡连通,下端插入水中,玻璃泡中封闭有一定质量的空气。若玻璃管中水柱上升,则外界大气的变化可能是( )
A.温度降低,压强增大
B.温度升高,压强不变
C.温度升高,压强减小
D.温度不变,压强减小
解析 由题意可知,玻璃泡中空气温度与大气温度相同,玻璃泡中空气体积随水柱的上升而减小。将玻璃泡中气体近似看成理想气体,根据理想气体状态方程=C,C为恒量,若温度降低,体积减小,压强可能增大、不变或减小,A正确;若温度升高,体积减小,压强一定增大,B、C错误;若温度不变,体积减小,压强一定增大,D错误。
答案 A
4.如图所示,为质量恒定的某种气体的p-T图像,A、B、C三态中体积最大的状态是( )
A.A状态 B.B状态
C.C状态 D.条件不足,无法确定
解析 由理想气体的状态方程=C变形后可得p=T,可见,图线斜率越小时体积越大,C正确。
答案 C
5.已知湖水深度为20 m,湖底水温为 4 ℃,水面温度为17 ℃,大气压强为1.0×105 Pa。当一气泡从湖底缓慢升到水面时,其体积约为原来的(g取10 m/s2,ρ水=1.0×103 kg/m3)( )
A.12.8倍 B.8.5倍
C.3.1倍 D.2.1倍
解析 p1=p0+ρgh=3.0×105 Pa,T0=4 K+273 K=277 K,T1=17 K+273 K=290 K,由=,解得≈3.1,C正确。
答案 C
6.(多选)一定质量的理想气体经历如图所示的一系列过程,ab、bc、cd和da这四个过程在p-T图上都是直线段,ab和dc的延长线通过坐标原点O,bc垂直于ab,ad平行于纵轴,由图可以判断( )
A.ab过程中气体体积不断减小
B.bc过程中气体体积不断减小
C.cd过程中气体体积不断增大
D.da过程中气体体积不断增大
解析 由p-T图线的特点可知a、b在同一条等容线上,体积不变,A错误;c、d在同一条等容线上,体积不变,C错误;在p-T图线中,图线的斜率越大与之对应的体积越小,因此b→c的过程体积减小,同理d→a的过程体积增大,B、D正确。
答案 BD
7.如图所示,圆柱形气缸A中用质量为2m的活塞封闭了一定质量的理想气体,气体温度为27 ℃,气缸中的活塞通过滑轮系统悬挂一质量为m的重物,稳定时活塞与气缸底部的距离为h,现在重物m上加挂一个质量为的小物体,已知大气压强为p0,活塞横截面积为S,m=,g为重力加速度,不计一切摩擦,求当气体温度升高到37 ℃且系统重新稳定后,重物m下降的高度。
解析 以气缸内的气体为研究对象,
初状态时,对活塞,由平衡条件得
p1S+mg=p0S+2mg,
气体压强p1=2p0,气体体积V1=hS,温度T1=300 K
末状态时,对活塞,由平衡条件得
p2S+mg=p0S+2mg
气体压强p2=p0,气体体积V2=(h+Δh)S,温度T2=310 K
根据理想气体状态方程:=
解得Δh=0.24h。
答案 0.24h
能力提升
8.(多选)一定质量理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则气体体积在( )
A.ab过程中不断增大
B.bc过程中保持不变
C.cd过程中不断增大
D.da过程中保持不变
解析 首先,因为bc的延长线通过原点,所以bc是等容线,即气体体积在bc过程中保持不变,B正确;ab是等温线,压强减小则体积增大,A正确;cd是等压线,温度降低则体积减小,C错误;连接aO交cd于e,如图所示,则ae是等容线,即Va=Ve,因为Vd<Ve,所以Vd<Va,da过程中体积不是保持不变,D错误。
答案 AB
9.光滑绝热的轻质活塞把密封的圆筒容器分成A、B两部分,这两部分充有温度相同的理想气体,平衡时VA∶VB=1∶2,现将A中气体加热到127 ℃,B中气体降低到27 ℃,待重新平衡后,这两部分气体体积的比VA′∶VB′为( )
A.1∶1 B.2∶3
C.3∶4 D.2∶1
解析 对A部分气体有:=①
对B部分气体有:=②
因为pA=pB,pA′=pB′,TA=TB,
所以将①÷②式得=
所以===。
答案 B
10.如图所示,一定质量的气体从状态A经状态B、C、D再回到状态A。问AB、BC、CD、DA是什么过程?已知气体在状态A时的体积是1 L,则在状态B、C、D时的体积各为多少?并把此图改为p-V图。
解析 AB过程是等容升温升压过程,BC过程是等压膨胀过程,CD过程是等温膨胀过程,DA过程是等压压缩过程。
现求A、B、C、D各点的体积:已知VA=1 L,VB=1 L(等容过程),
由=(等压过程),
得VC=TC=900× L=2 L;
由pDVD=pCVC(等温过程),
得VD=VC=2× L=6 L。
改画为p-V图如图所示。
答案 见解析
11.一水银气压计中混进了空气,因而在外界温度为27 ℃、大气压为758 mmHg时,这个水银气压计的读数为738 mmHg,此时管中水银面距管顶80 mm,当温度降至-3 ℃时,这个气压计的读数为743 mmHg,求此时外界的实际大气压值为多少mmHg?
解析 画出该题初、末状态的示意图:
分别写出水银气压计中气体的初、末状态的状态参量:
p1=758 mmHg-738 mmHg=20 mmHg
V1=(80 mm)·S
T1=(273+27) K=300 K
p2=p-743 mmHg
V2=(738+80)mm·S-(743 mm)·S=(75 mm)·S
T2=(273-3) K=270 K
由理想气体状态方程:
=
解得p=762.2 mmHg。
答案 762.2 mmHg
12.如图所示,一固定的竖直气缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞。已知大活塞的质量为m1=2.50 kg,横截面积为S1=80.0 cm2;小活塞的质量为m2=1.50 kg,横截面积为S2=40.0 cm2;两活塞用刚性轻杆连接,间距保持为l=40.0 cm;气缸外大气的压强为p=1.00×105 Pa,温度为T=303 K。初始时大活塞与大圆筒底部相距,两活塞间封闭气体的温度为T1=495 K。现气缸内气体温度缓慢下降,活塞缓慢下移。忽略两活塞与气缸壁之间的摩擦,重力加速度大小g取 10 m/s2。求:
(1)在大活塞与大圆筒底部接触前的瞬间,缸内封闭气体的温度;
(2)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强。
解析 (1)大、小活塞在缓慢下移过程中,受力情况不变,气缸内气体压强不变,由盖—吕萨克定律得=
初状态V1=(S1+S2),T1=495 K
末状态V2=lS2
解得T2=T1=330 K
(2)在大活塞与大圆筒底部接触前的瞬间,对大、小活塞受力分析则有
m1g+m2g+pS1+p1S2=p1S1+pS2
解得p1=1.1×105 Pa
缸内封闭的气体与缸外大气达到热平衡过程中,气体体积不变,由查理定律得
=
T3=T=303 K
解得p2=1.01×105 Pa。
答案 (1)330 K (2)1.01×105 Pa
同课章节目录
- 第1章 分子动理论与气体实验定律
- 第1节 分子动理论的基本观点
- 第2节 科学测量:用油膜法估测油酸分子的大小
- 第3节 气体分子速率分布的统计规律
- 第4节 科学探究:气体压强与体积的关系
- 第5节 气体实验定律
- 第2章 固体与液体
- 第1节 固体类型及微观结构
- 第2节 表面张力和毛细现象
- 第3节 材料及其应用
- 第3章 热力学定律
- 第1节 热力学第一定律
- 第2节 能量的转化与守恒
- 第3节 热力学第二定律
- 第4节 熵——系统无序程度的量度
- 第4章 原子结构
- 第1节 电子的发现与汤姆孙原子模型
- 第2节 原子的核式结构模型
- 第3节 光谱与氢原子光谱
- 第4节 玻尔原子模型
- 第5章 原子核与核能
- 第1节 认识原子核
- 第2节 原子核衰变及半衰期
- 第3节 核力与核能
- 第4节 核裂变和核聚变
- 第5节 核能的利用与环境保护
- 第6章 波粒二象性
- 第1节 光电效应及其解释
- 第2节 实物粒子的波粒二象性
