九年级数学圆周角定理及其推论(共18张ppt)
文档属性
| 名称 | 九年级数学圆周角定理及其推论(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
复习导入
你还记得什么是圆心角吗?
O
A
B
顶点在圆心的角叫圆心角。
探究新知part1
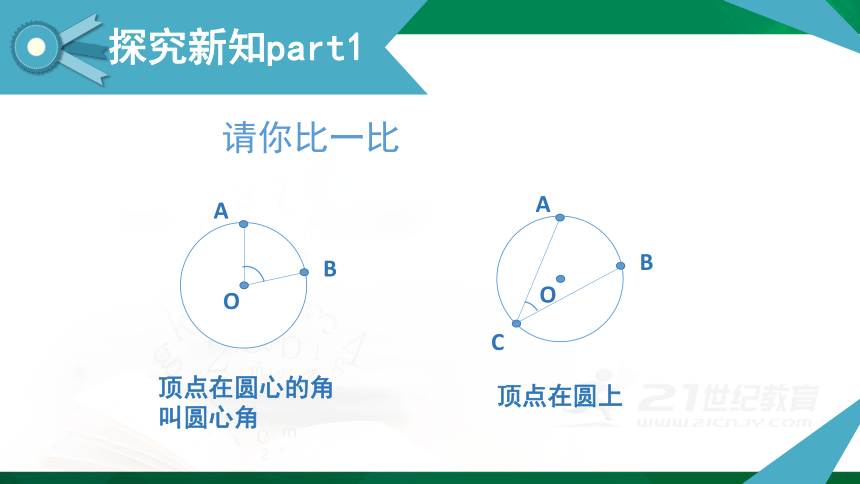
请你比一比
O
A
B
顶点在圆上
O
A
B
C
顶点在圆心的角
叫圆心角
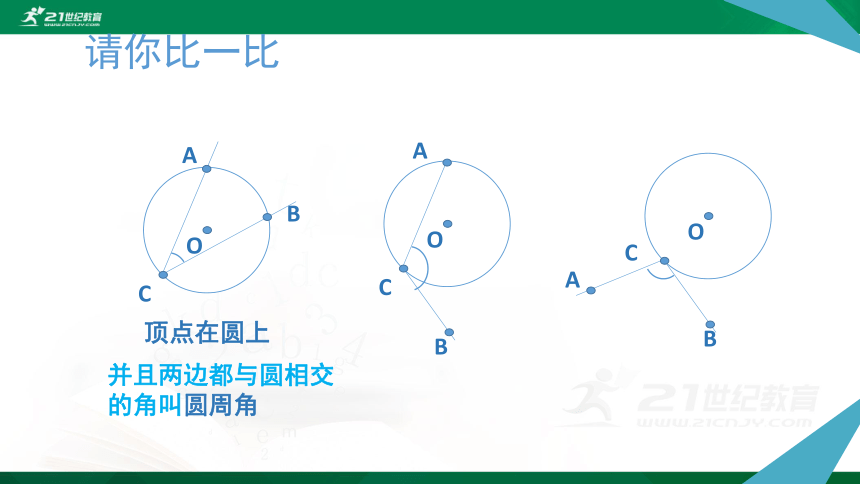
请你比一比
顶点在圆上
O
A
B
C
O
A
C
B
O
C
B
A
并且两边都与圆相交
的角叫圆周角
请你想一想
O
A
B
顶点在圆上
O
A
B
C
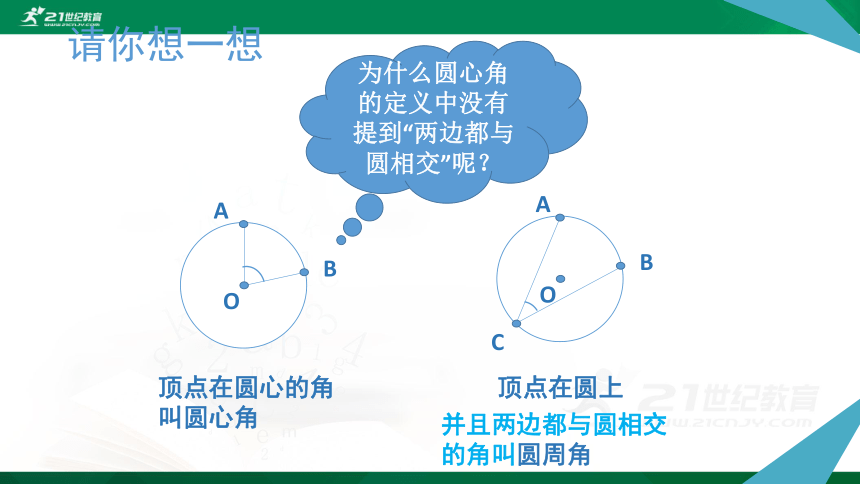
顶点在圆心的角
叫圆心角
并且两边都与圆相交
的角叫圆周角
为什么圆心角的定义中没有提到“两边都与圆相交”呢?
请你练一练
判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
P
不是,顶点不在圆上
是
不是,两边不与圆相交
不是,只有一边与圆相交
请你练一练
下列图形中的∠ACB是圆周角吗?
C
C
C
B
B
B
A
A
A
O
O
O
观察各图形中圆周角∠ACB与圆心的位置关系
圆心在角外
圆心在角内
圆心在角的一边上
探究新知part2
请你画一画
请你在⊙O上任取一段弧AB,做出这段弧所对的圆周角∠ACB,
A
C
B
O
A
C
B
O
C
B
A
O
同弧所对的圆周角等于它所对的圆心角的一半
连接AO和BO,我们会也得到圆心角∠AOB
圆周角∠ACB和圆心角∠AOB对着同一段弧AB
请你来证明1
C
B
A
O
同弧所对的圆周角等于它所对的圆心角的一半
圆心在圆周角的一条边上
∵AO=CO
∴∠C=∠A
又∵∠AOB=∠C+∠A
∴∠AOB=2∠C
即∠C=
∠AOB
1
2
请你来证明2
同弧所对的圆周角等于它所对的圆心角的一半
圆心在圆周角内部
A
C
B
O
D
C
D
A
O
∵AO=CO
∴∠ACD=∠A
又∵∠AOD=∠ACD+∠A
∴∠AOD=2∠ACD
即∠ACD=
∠AOD
同理∠BCD=
∠BOD
∴∠ACD+∠BCD=
(∠AOD+∠BOD)
即∠ACB=
∠AOB
1
2
2
1
2
1
1
2
证明:作直径CD
提示:过点C做直径CD,转化为圆心在圆周角一条边上的情况
请你来证明3
同弧所对的圆周角等于它所对的圆心角的一半
圆心在圆周角的外部
C
B
A
O
D
∵AO=CO
∴∠ACD=∠A
又∵∠AOD=∠ACD+∠A
∴∠AOD=2∠ACD
即∠ACD=
∠AOD
同理∠BCD=
∠BOD
∴∠ACD-∠BCD=
(∠AOD-∠BOD)
即∠ACB=
∠AOB
1
2
2
1
2
1
1
2
证明:作直径CD
归纳
同弧所对的圆周角等于它所对的圆心角的一半
圆周角定理:
C
B
A
O
几何表达:
∠ACB=
∠AOB
或∠AOB=2∠ACB
1
2
巩固练习
1请找出下图中弧AB所对的圆周角和圆心角,若∠C为55°,则∠AOB为多少度,∠D和∠E又分别是多少度?
C
B
A
O
D
E
由此,你有什么发现,能得出什么结论
探究新知part3
∵∠C=55°
∴∠AOB=2∠C=110°
∴∠D=
∠AOB=55°
同理∠E=
55°
归纳
同弧或等弧所对的圆周角相等
圆周角定理的推论一:
C
B
A
O
D
几何表达:∠C=∠D
C
B
A
O
D
E
F
⌒
同弧(AB):
⌒
⌒
∵
AB
=
CD
∴
∠E=∠F
⌒
⌒
等弧(AB和CD):
1
如图
A,B,C,D是⊙O上的点,则图中与∠A相等的角是(
)
A.∠B
B.∠C
C.∠DEB
D.∠D
A
B
C
D
O
巩固练习
⌒
⌒
2
如图
所示,四边形ABCD的四个顶点均在⊙O上,AB=BC
∠BAC=25°,则∠BDC=
,∠BDA=
.
C
A
B
D
O
⌒
⌒
3
如图
A,B,C,D是⊙O上的点,AB=BC,∠CDB=25°,
则∠AOB=
.
C
A
B
D
O
E
归纳
我们今天学习了哪些内容
课堂小结
同弧所对的圆周角等于它所对的圆心角的一半
圆周角定理:
同弧或等弧所对的圆周角相等
圆周角定理的推论一:
圆周角的定义:
顶点在圆上并且两边都与圆相交的角叫圆周角
复习导入
你还记得什么是圆心角吗?
O
A
B
顶点在圆心的角叫圆心角。
探究新知part1
请你比一比
O
A
B
顶点在圆上
O
A
B
C
顶点在圆心的角
叫圆心角
请你比一比
顶点在圆上
O
A
B
C
O
A
C
B
O
C
B
A
并且两边都与圆相交
的角叫圆周角
请你想一想
O
A
B
顶点在圆上
O
A
B
C
顶点在圆心的角
叫圆心角
并且两边都与圆相交
的角叫圆周角
为什么圆心角的定义中没有提到“两边都与圆相交”呢?
请你练一练
判断下列图形中所画的∠P是否为圆周角?并说明理由。
P
P
P
P
不是,顶点不在圆上
是
不是,两边不与圆相交
不是,只有一边与圆相交
请你练一练
下列图形中的∠ACB是圆周角吗?
C
C
C
B
B
B
A
A
A
O
O
O
观察各图形中圆周角∠ACB与圆心的位置关系
圆心在角外
圆心在角内
圆心在角的一边上
探究新知part2
请你画一画
请你在⊙O上任取一段弧AB,做出这段弧所对的圆周角∠ACB,
A
C
B
O
A
C
B
O
C
B
A
O
同弧所对的圆周角等于它所对的圆心角的一半
连接AO和BO,我们会也得到圆心角∠AOB
圆周角∠ACB和圆心角∠AOB对着同一段弧AB
请你来证明1
C
B
A
O
同弧所对的圆周角等于它所对的圆心角的一半
圆心在圆周角的一条边上
∵AO=CO
∴∠C=∠A
又∵∠AOB=∠C+∠A
∴∠AOB=2∠C
即∠C=
∠AOB
1
2
请你来证明2
同弧所对的圆周角等于它所对的圆心角的一半
圆心在圆周角内部
A
C
B
O
D
C
D
A
O
∵AO=CO
∴∠ACD=∠A
又∵∠AOD=∠ACD+∠A
∴∠AOD=2∠ACD
即∠ACD=
∠AOD
同理∠BCD=
∠BOD
∴∠ACD+∠BCD=
(∠AOD+∠BOD)
即∠ACB=
∠AOB
1
2
2
1
2
1
1
2
证明:作直径CD
提示:过点C做直径CD,转化为圆心在圆周角一条边上的情况
请你来证明3
同弧所对的圆周角等于它所对的圆心角的一半
圆心在圆周角的外部
C
B
A
O
D
∵AO=CO
∴∠ACD=∠A
又∵∠AOD=∠ACD+∠A
∴∠AOD=2∠ACD
即∠ACD=
∠AOD
同理∠BCD=
∠BOD
∴∠ACD-∠BCD=
(∠AOD-∠BOD)
即∠ACB=
∠AOB
1
2
2
1
2
1
1
2
证明:作直径CD
归纳
同弧所对的圆周角等于它所对的圆心角的一半
圆周角定理:
C
B
A
O
几何表达:
∠ACB=
∠AOB
或∠AOB=2∠ACB
1
2
巩固练习
1请找出下图中弧AB所对的圆周角和圆心角,若∠C为55°,则∠AOB为多少度,∠D和∠E又分别是多少度?
C
B
A
O
D
E
由此,你有什么发现,能得出什么结论
探究新知part3
∵∠C=55°
∴∠AOB=2∠C=110°
∴∠D=
∠AOB=55°
同理∠E=
55°
归纳
同弧或等弧所对的圆周角相等
圆周角定理的推论一:
C
B
A
O
D
几何表达:∠C=∠D
C
B
A
O
D
E
F
⌒
同弧(AB):
⌒
⌒
∵
AB
=
CD
∴
∠E=∠F
⌒
⌒
等弧(AB和CD):
1
如图
A,B,C,D是⊙O上的点,则图中与∠A相等的角是(
)
A.∠B
B.∠C
C.∠DEB
D.∠D
A
B
C
D
O
巩固练习
⌒
⌒
2
如图
所示,四边形ABCD的四个顶点均在⊙O上,AB=BC
∠BAC=25°,则∠BDC=
,∠BDA=
.
C
A
B
D
O
⌒
⌒
3
如图
A,B,C,D是⊙O上的点,AB=BC,∠CDB=25°,
则∠AOB=
.
C
A
B
D
O
E
归纳
我们今天学习了哪些内容
课堂小结
同弧所对的圆周角等于它所对的圆心角的一半
圆周角定理:
同弧或等弧所对的圆周角相等
圆周角定理的推论一:
圆周角的定义:
顶点在圆上并且两边都与圆相交的角叫圆周角
同课章节目录
