湘教版八年级数学下册第2章 四边形单元测试题(word含答案)
文档属性
| 名称 | 湘教版八年级数学下册第2章 四边形单元测试题(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 215.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 18:35:51 | ||
图片预览




文档简介
第2章 四边形
一、选择题(本大题共9小题,每小题4分,共36分)
1.下面几种中式窗户图形既是轴对称图形又是中心对称图形的是
( )
图1
2.菱形不具备的性质是
( )
A.是轴对称图形
B.是中心对称图形
C.对角线互相垂直
D.对角线一定相等
3.若一个多边形的内角和为1080°,则这个多边形的边数为
( )
A.6
B.7
C.8
D.9
4如图2,M,N分别是△ABC的边AB,AC的中点,若∠A=65°,∠ANM=45°,则
∠B等于
( )
图2
A.20°
B.45°
C.65°
D.70°
5.已知?ABCD中,有下列条件:
①AB=BC;②AC=BD;③AC⊥BD;④AC平分∠BAD,其中能说明?ABCD是矩形的是
( )
A.①
B.②
C.③
D.④
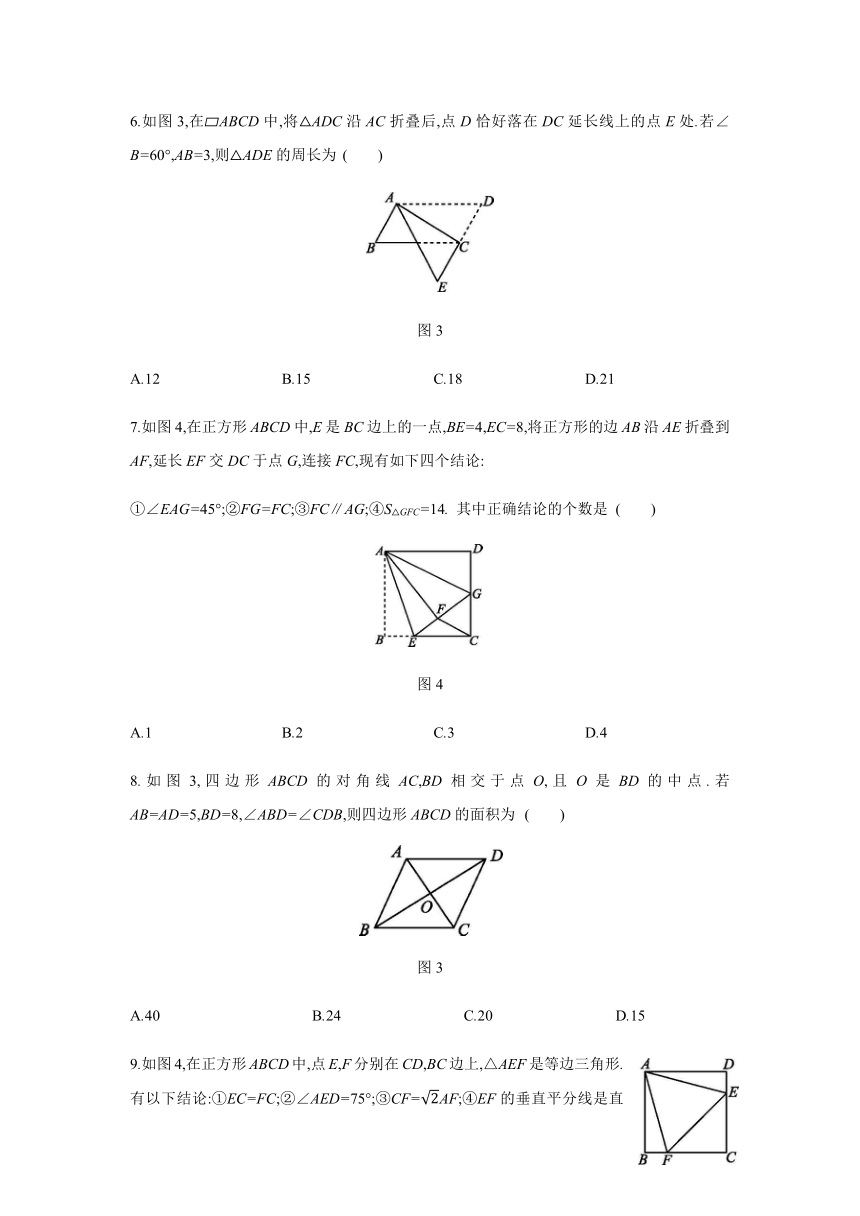
6.如图3,在?ABCD中,将△ADC沿AC折叠后,点D恰好落在DC延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为
( )
图3
A.12
B.15
C.18
D.21
7.如图4,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形的边AB沿AE折叠到AF,延长EF交DC于点G,连接FC,现有如下四个结论:
①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.
其中正确结论的个数是
( )
图4
A.1
B.2
C.3
D.4
8.如图3,四边形ABCD的对角线AC,BD相交于点O,且O是BD的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为
( )
图3
A.40
B.24
C.20
D.15
9.如图4,在正方形ABCD中,点E,F分别在CD,BC边上,△AEF是等边三角形.有以下结论:①EC=FC;②∠AED=75°;③CF=AF;④EF的垂直平分线是直线AC.正确结论的个数是( )
A.1
B.2
C.3
D.4
图4
二、
填空题(本大题共5小题,每小题5分,共25分)
10在平行四边形ABCD中,∠A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于 .?
11如图5,在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= °.?
图5
图6
12
如图6,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为E,且AE平分∠BAC,则AB的长为 .?
13.如图7,在矩形ABCD中,AD=,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB= .?
图7
14.图8为某城市部分街道的示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD于点E,GF⊥BC于点F,AD=1500
m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100
m,则小聪行走的路程为 m.?
图8
三、解答题(本大题共4小题,共39分)
15
如图7,在平行四边形ABCD中,点E,F分别在BC,AD上,AC与EF相交于点O,且AO=CO.
(1)求证:△AOF≌△COE;
(2)连接AE,CF,四边形AECF (填“是”或“不是”)平行四边形.?
图7
16如图8,在?ABCD中,BC=2AB,AB⊥AC,分别在边BC,AD上的点E与点F关于AC对称,连接EF,AE,CF,DE.
(1)试判断四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
图8
17
如图9,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF,连接OE.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
图9
18
如图10,在正方形ABCD中,E是DC边上一点(与点D,C不重合),连接AE,将△ADE沿AE所在的直线折叠,得到△AFE,延长EF交BC于点G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角的平分线),并说明理由.
图10
答案
1.
C 2.
D 3.
C 4.
D 5.
B 6.
C 7.
B
8.
B 9.C
10.16或8
11.61
12.
13.
14.4600
15.解:
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAO=∠ECO.
在△AOF和△COE中,
∴△AOF≌△COE(ASA).
(2)是
16.解:(1)四边形AECF为菱形.理由如下:
在?ABCD中,AD∥BC,∴∠CAF=∠ACE.设AC与EF相交于点O.
∵分别在边BC,AD上的点E与点F关于AC对称,
∴OE=OF,EF⊥AC.
在△AOF和△COE中,
∴△AOF≌△COE,∴OA=OC.
又OE=OF,EF⊥AC,
∴四边形AECF为菱形.
(2)证明:∵AB⊥AC,EF⊥AC,∴EF∥AB.
又∵OA=OC,
∴BE=CE=BC,OE=AB.
∵BC=2AB,∴EF=AB=BE=CE.
∵四边形ABCD是平行四边形,∴AD=BC.
又∵AF=EC,∴AF=DF=EF.
∴AE⊥DE.
17.解:(1)证明:∵四边形ABCD为菱形,
∴O为BD的中点.
∵E为AD的中点,
∴OE为△ABD的中位线,∴OE∥FG.
又∵OG∥EF,∴四边形OEFG为平行四边形.又∵EF⊥AB,∴四边形OEFG为矩形.
(2)∵E为AD的中点,AD=10,
∴AE=AD=5.∵∠EFA=90°,EF=4,
∴在Rt△AEF中,AF===3.
∵四边形ABCD为菱形,
∴AB=AD=10,∴OE=AB=5.
∵四边形OEFG为矩形,∴FG=OE=5,
∴BG=AB-AF-FG=10-3-5=2.
18.解:AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCN的平分线,GH是∠EGM的平分线.
理由:如图,过点H作HN⊥BM于点N,则∠HNC=90°.
∵四边形ABCD为正方形,
∴AD=AB=BC,∠D=∠DAB=∠B=∠DCB=∠DCM=90°.
①∵将△ADE沿AE所在的直线折叠得到△AFE,
∴△ADE≌△AFE,
∴∠D=∠AFE=90°,AD=AF,∠DAE=∠FAE,
∴∠AFG=90°,AF=AB.
又∵AG=AG,∴Rt△ABG≌Rt△AFG(HL),
∴∠BAG=∠FAG,∠AGB=∠AGF,
∴AG是∠BAF的平分线,GA是∠BGF的平分线;
②由①知,∠DAE=∠FAE,∠BAG=∠FAG.
又∵∠DAB=90°,
∴∠GAF+∠EAF=×90°=45°,
即∠GAH=45°.
∵GH⊥AG,∴∠GHA=90°-∠GAH=45°,
∴△AGH为等腰直角三角形,∴AG=GH.
∵∠AGB+∠BAG=90°,
∠AGB+∠NGH=90°,
∴∠BAG=∠NGH.
又∵∠B=∠HNG=90°,AG=GH,
∴△ABG≌△GNH(AAS),
∴BG=NH,AB=GN,∴BC=GN,
∴BC-CG=GN-CG,
即BG=CN,∴CN=NH.
∵∠HNC=90°,
∴∠NCH=∠NHC=×90°=45°,
∴∠DCH=∠DCM-∠NCH=45°,
∴∠DCH=∠NCH,
∴CH是∠DCN的平分线;
③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,
由①知,∠AGB=∠AGF,
∴∠HGN=∠EGH,
∴GH是∠EGM的平分线.
一、选择题(本大题共9小题,每小题4分,共36分)
1.下面几种中式窗户图形既是轴对称图形又是中心对称图形的是
( )
图1
2.菱形不具备的性质是
( )
A.是轴对称图形
B.是中心对称图形
C.对角线互相垂直
D.对角线一定相等
3.若一个多边形的内角和为1080°,则这个多边形的边数为
( )
A.6
B.7
C.8
D.9
4如图2,M,N分别是△ABC的边AB,AC的中点,若∠A=65°,∠ANM=45°,则
∠B等于
( )
图2
A.20°
B.45°
C.65°
D.70°
5.已知?ABCD中,有下列条件:
①AB=BC;②AC=BD;③AC⊥BD;④AC平分∠BAD,其中能说明?ABCD是矩形的是
( )
A.①
B.②
C.③
D.④
6.如图3,在?ABCD中,将△ADC沿AC折叠后,点D恰好落在DC延长线上的点E处.若∠B=60°,AB=3,则△ADE的周长为
( )
图3
A.12
B.15
C.18
D.21
7.如图4,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形的边AB沿AE折叠到AF,延长EF交DC于点G,连接FC,现有如下四个结论:
①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.
其中正确结论的个数是
( )
图4
A.1
B.2
C.3
D.4
8.如图3,四边形ABCD的对角线AC,BD相交于点O,且O是BD的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为
( )
图3
A.40
B.24
C.20
D.15
9.如图4,在正方形ABCD中,点E,F分别在CD,BC边上,△AEF是等边三角形.有以下结论:①EC=FC;②∠AED=75°;③CF=AF;④EF的垂直平分线是直线AC.正确结论的个数是( )
A.1
B.2
C.3
D.4
图4
二、
填空题(本大题共5小题,每小题5分,共25分)
10在平行四边形ABCD中,∠A=30°,AD=4,BD=4,则平行四边形ABCD的面积等于 .?
11如图5,在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= °.?
图5
图6
12
如图6,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为E,且AE平分∠BAC,则AB的长为 .?
13.如图7,在矩形ABCD中,AD=,F是DA延长线上一点,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F=20°,则AB= .?
图7
14.图8为某城市部分街道的示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD于点E,GF⊥BC于点F,AD=1500
m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F,若小敏行走的路程为3100
m,则小聪行走的路程为 m.?
图8
三、解答题(本大题共4小题,共39分)
15
如图7,在平行四边形ABCD中,点E,F分别在BC,AD上,AC与EF相交于点O,且AO=CO.
(1)求证:△AOF≌△COE;
(2)连接AE,CF,四边形AECF (填“是”或“不是”)平行四边形.?
图7
16如图8,在?ABCD中,BC=2AB,AB⊥AC,分别在边BC,AD上的点E与点F关于AC对称,连接EF,AE,CF,DE.
(1)试判断四边形AECF的形状,并说明理由;
(2)求证:AE⊥DE.
图8
17
如图9,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF,连接OE.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BG的长.
图9
18
如图10,在正方形ABCD中,E是DC边上一点(与点D,C不重合),连接AE,将△ADE沿AE所在的直线折叠,得到△AFE,延长EF交BC于点G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角的平分线),并说明理由.
图10
答案
1.
C 2.
D 3.
C 4.
D 5.
B 6.
C 7.
B
8.
B 9.C
10.16或8
11.61
12.
13.
14.4600
15.解:
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAO=∠ECO.
在△AOF和△COE中,
∴△AOF≌△COE(ASA).
(2)是
16.解:(1)四边形AECF为菱形.理由如下:
在?ABCD中,AD∥BC,∴∠CAF=∠ACE.设AC与EF相交于点O.
∵分别在边BC,AD上的点E与点F关于AC对称,
∴OE=OF,EF⊥AC.
在△AOF和△COE中,
∴△AOF≌△COE,∴OA=OC.
又OE=OF,EF⊥AC,
∴四边形AECF为菱形.
(2)证明:∵AB⊥AC,EF⊥AC,∴EF∥AB.
又∵OA=OC,
∴BE=CE=BC,OE=AB.
∵BC=2AB,∴EF=AB=BE=CE.
∵四边形ABCD是平行四边形,∴AD=BC.
又∵AF=EC,∴AF=DF=EF.
∴AE⊥DE.
17.解:(1)证明:∵四边形ABCD为菱形,
∴O为BD的中点.
∵E为AD的中点,
∴OE为△ABD的中位线,∴OE∥FG.
又∵OG∥EF,∴四边形OEFG为平行四边形.又∵EF⊥AB,∴四边形OEFG为矩形.
(2)∵E为AD的中点,AD=10,
∴AE=AD=5.∵∠EFA=90°,EF=4,
∴在Rt△AEF中,AF===3.
∵四边形ABCD为菱形,
∴AB=AD=10,∴OE=AB=5.
∵四边形OEFG为矩形,∴FG=OE=5,
∴BG=AB-AF-FG=10-3-5=2.
18.解:AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCN的平分线,GH是∠EGM的平分线.
理由:如图,过点H作HN⊥BM于点N,则∠HNC=90°.
∵四边形ABCD为正方形,
∴AD=AB=BC,∠D=∠DAB=∠B=∠DCB=∠DCM=90°.
①∵将△ADE沿AE所在的直线折叠得到△AFE,
∴△ADE≌△AFE,
∴∠D=∠AFE=90°,AD=AF,∠DAE=∠FAE,
∴∠AFG=90°,AF=AB.
又∵AG=AG,∴Rt△ABG≌Rt△AFG(HL),
∴∠BAG=∠FAG,∠AGB=∠AGF,
∴AG是∠BAF的平分线,GA是∠BGF的平分线;
②由①知,∠DAE=∠FAE,∠BAG=∠FAG.
又∵∠DAB=90°,
∴∠GAF+∠EAF=×90°=45°,
即∠GAH=45°.
∵GH⊥AG,∴∠GHA=90°-∠GAH=45°,
∴△AGH为等腰直角三角形,∴AG=GH.
∵∠AGB+∠BAG=90°,
∠AGB+∠NGH=90°,
∴∠BAG=∠NGH.
又∵∠B=∠HNG=90°,AG=GH,
∴△ABG≌△GNH(AAS),
∴BG=NH,AB=GN,∴BC=GN,
∴BC-CG=GN-CG,
即BG=CN,∴CN=NH.
∵∠HNC=90°,
∴∠NCH=∠NHC=×90°=45°,
∴∠DCH=∠DCM-∠NCH=45°,
∴∠DCH=∠NCH,
∴CH是∠DCN的平分线;
③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,
由①知,∠AGB=∠AGF,
∴∠HGN=∠EGH,
∴GH是∠EGM的平分线.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
