湘教版(2012)初中数学九年级上册 1.1.2 反比例函数说课 课件(26张)
文档属性
| 名称 | 湘教版(2012)初中数学九年级上册 1.1.2 反比例函数说课 课件(26张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
反比例函数说课稿
今天我说课的内容反比例函数的性质。主要让学生经历通过观察特例,归纳反比例函数的性质的过程,让学生体会到数学的三种主要数学思想----从特殊到一般、图形结合、类比。
我将从以下个方面来对本课进行说明。
学情分析:八年级已经学习了一次函数,对函数的学习方法和思路有一定的了解。再经过前面几课时的学习,学生较好的掌握了反比例函数的图像与系数k的关系,为今天的学习打下来较好的基础。
教材分析:本节课的内容是理解并掌握反比例函数的性质。
包括四个知识点:反比例函数的性质与系数k的关系、
系数k的几何含义。依照教材和教学大纲的要求,为了
能更好的完成本节课的教学目标,我制定了本节课教
学的重、难点。
重点:本节教学的重点是理解反比例函数的性质。
难点:能运用反比例函数的性质解决一些简单问题。
根据以上的教学分析,制定本节课的教法和学法。
教法学法:我把本节教学分为五部分。1、创设情景、激趣设疑,通过回顾前面所学,自然地设疑,激发学生学习兴趣;2、结合观察图像,发现问题,3、小组交流,在班上展示;本学段教法和学法遵循了有利于学生自主探索,动手实践、合作交流。4、归纳总结,学生通过观察、思考发现反比例函数的性质;我安排观察发现、分析归纳的发现学习法。5、精讲精练,逐步巩固加深所学。
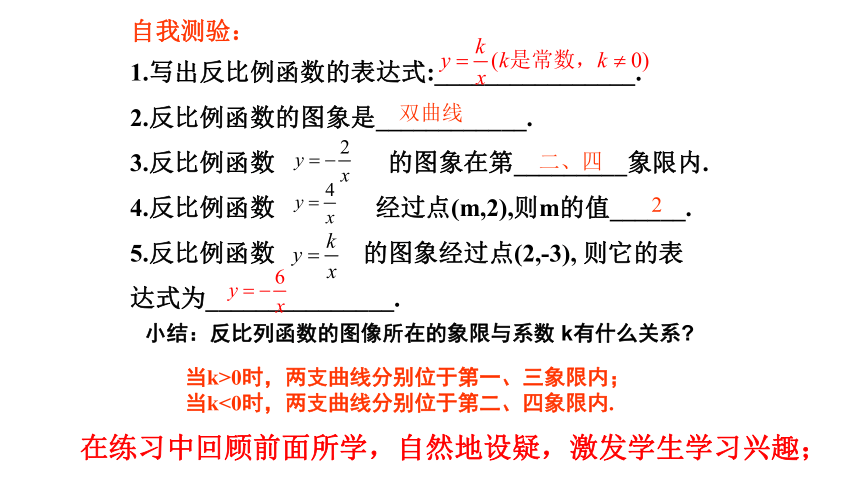
自我测验:
1.写出反比例函数的表达式:________________.
2.反比例函数的图象是____________.
3.反比例函数 的图象在第_________象限内.
4.反比例函数 经过点(m,2),则m的值______.
5.反比例函数 的图象经过点(2,-3), 则它的表
达式为_______________.
双曲线
2
二、四
小结:反比列函数的图像所在的象限与系数 k有什么关系
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
在练习中回顾前面所学,自然地设疑,激发学生学习兴趣;
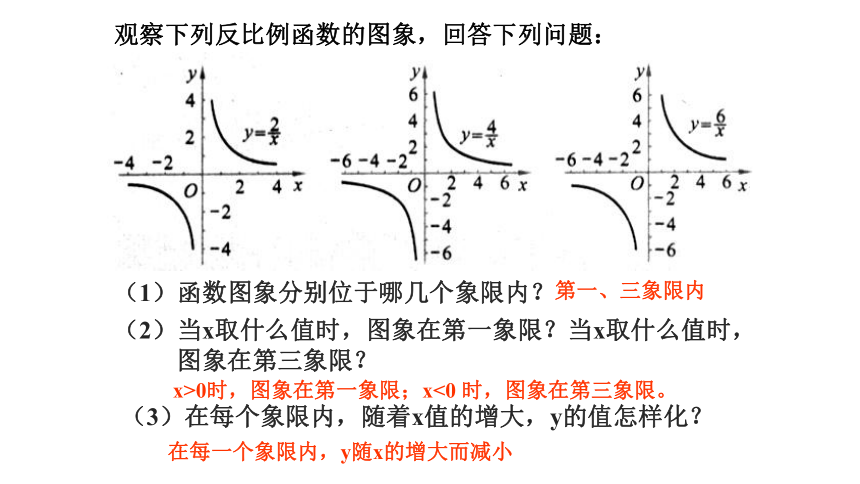
观察下列反比例函数的图象,回答下列问题:
(1)函数图象分别位于哪几个象限内?
第一、三象限内
x>0时,图象在第一象限;x<0 时,图象在第三象限。
在每一个象限内,y随x的增大而减小
(2)当x取什么值时,图象在第一象限?当x取什么值时,
图象在第三象限?
(3)在每个象限内,随着x值的增大,y的值怎样化?
如果k=-2, -4,-6,那么
的图象有又什么共同特征?
(1)函数图象分别位于哪个象限内?
x>0时,图象在第四象限;x<0 时,图象在第二象限
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一个象限内,y随x的增大而增大
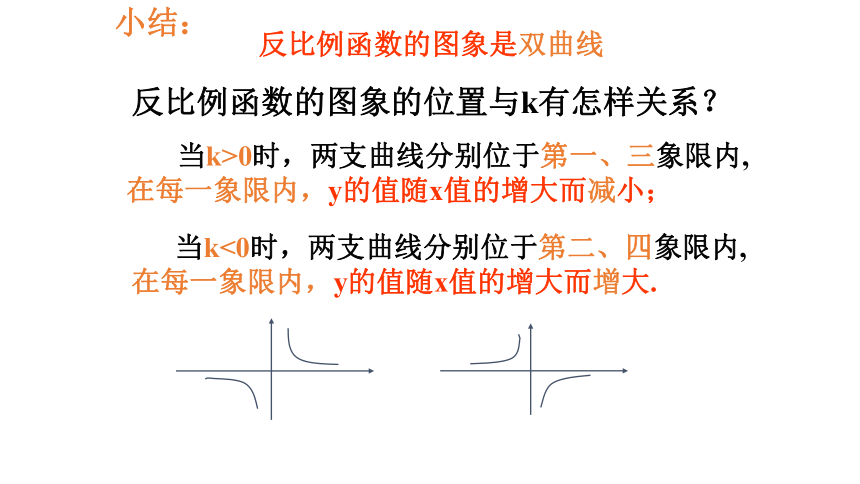
小结:
反比例函数的图象的位置与k有怎样关系?
当k>0时,两支曲线分别位于第一、三象限内,
在每一象限内,y的值随x值的增大而减小;
反比例函数的图象是双曲线
当k<0时,两支曲线分别位于第二、四象限内,
在每一象限内,y的值随x值的增大而增大.
在这个练习中,我引导学生结合观察图像,探索比较、发现规律:通过不同情况的比较,较全面的掌握反比例函数的性质。并进一步在小组中交流,在班上展示;本学段教法和学法遵循了有利于学生自主探索,动手实践、合作交流。学生通过观察、思考发现反比例函数的性质;我安排观察发现、分析归纳的发现学习法。
1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________.
(1)(2)(3)
(4)
随堂练习一
通过这一练习,初步检测学生掌握知识、运用知识的情况
2.若反比函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
3.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
在实际问题中
图象就可能只
有一支.
特别提醒
在前面练习的基础上,适当的引入学生最熟悉
的行程问题,提高了练习的难度和广度,进一
步提高学生运用知识解决问题的能力。
随堂练习二:
1.下列函数中,其图象位于第一、三象限的有__________;
在其所在的象限内,y随x的增大而增大的有___________.
2.(1) 已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数 的
图象上,比较y1、 y2 、y3的大小关系。
解:∵ k=4>0
∴ 图象在第一、三象限内,每一象限内y随x的增大而减小
∵ x10, ∴点A(-2,y1),点B(-1,y2)在第三象限
点C(3,y3)在第一象限。
∴ y3>0, y2(1)(2)(3)
(4)
本节练习注重学生明晰理由,
养成言之有理的严谨的数学学习习惯
通过这两节练习,是学生更好地理解知识,
运用知识,由易到难安排了两组练习,有
效拓展学生的知识面。
解:当k>0时, y2 < y1 < 0< y3.
当k<0时, y3 < 0 < y1 < y2.
(2)如果点A(-2,y1),B(-1,y2)和C(3,y3)都在反比例函数 的图象上,那么y1、 y2 、y3的大小关系又如何呢?
挑战自我:
学无止境,勇攀高峰
如图,已知过反比例函数 的图像上一点A
作 轴于点B,若三角形AOB的面积为2,
则K=_____________。
-2
在师生双边、学生多边的交流中,进行探究、合作、
创新,在努力完成挑战自我、勇攀高峰环节中,争取
大部分学生获得成就感,持续激发学生爱数学、用数
学的积极性。进一步激发学生自主探究与学习热情,
体会到学无止境,也较好的照顾了学习能力较强的学生。
观察反比例函数图象的两支曲线,回答下列问题:
(1)它们会与坐标轴相交吗?
(2)反比例函数的图象是中心对称图形吗?
(3)反比例函数的图象是轴对称图形吗?
它们都不与坐标轴相交。
是轴对称图形,它们有两条对称轴.
是中心对称图形,对称中心是坐标原点.
议一议
函数 正比例函数 反比例函数
表达式
图象
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
在一三象限
y随x的增大而增大
经过一三象限
每个象限内, y随x的增大而减小
经过二四象限
在二四象限
y随x的增大而减小
每个象限内, y随x的增大而增大
填表分析正比例函数和反比例函数的区别
通过以上两个练习,学生在探索比较中发现规律,由此
自然地回顾本节课所学知识,并进一步通过横向比较,
总结正比例函数与反比例函数的异同,培养学生总结、
归纳知识的学习能力
1. 已知反比例函数 ,y随x的增
大而减小,求 的值和表达式.
提高练习:
O
x
y
A
C
O
x
y
D
x
y
o
O
x
y
B
D
1、反比例函数的性质: 反比例函数y=k/x的图象,当k>0时,图象位于第一、三象限,在每一象限内,y的值随x的增大而减小; 当k<0时,图象位于第二、四象限,y的值随x的增大而增大。
2、双曲线的两条分支逼近坐标轴但不可能与坐标轴相交。
3、反比例函数的图象是一个以原点为对称中心的中心对称图形。
4、在反比例函数y=k/x的图象上任取一点,分别作坐标轴的垂线(或平行线),与坐标轴所围成的S矩形=| k |
回顾与思考
回顾与反思,学生分组讨论、总结本节课所学的知识和技能。经过师生双边和学生多边的交流,使学生经历知识的形成与应用过程,达到学生所要掌握的基本知识与基本技能,发展应用数学的意义。
反比例函数说课稿
今天我说课的内容反比例函数的性质。主要让学生经历通过观察特例,归纳反比例函数的性质的过程,让学生体会到数学的三种主要数学思想----从特殊到一般、图形结合、类比。
我将从以下个方面来对本课进行说明。
学情分析:八年级已经学习了一次函数,对函数的学习方法和思路有一定的了解。再经过前面几课时的学习,学生较好的掌握了反比例函数的图像与系数k的关系,为今天的学习打下来较好的基础。
教材分析:本节课的内容是理解并掌握反比例函数的性质。
包括四个知识点:反比例函数的性质与系数k的关系、
系数k的几何含义。依照教材和教学大纲的要求,为了
能更好的完成本节课的教学目标,我制定了本节课教
学的重、难点。
重点:本节教学的重点是理解反比例函数的性质。
难点:能运用反比例函数的性质解决一些简单问题。
根据以上的教学分析,制定本节课的教法和学法。
教法学法:我把本节教学分为五部分。1、创设情景、激趣设疑,通过回顾前面所学,自然地设疑,激发学生学习兴趣;2、结合观察图像,发现问题,3、小组交流,在班上展示;本学段教法和学法遵循了有利于学生自主探索,动手实践、合作交流。4、归纳总结,学生通过观察、思考发现反比例函数的性质;我安排观察发现、分析归纳的发现学习法。5、精讲精练,逐步巩固加深所学。
自我测验:
1.写出反比例函数的表达式:________________.
2.反比例函数的图象是____________.
3.反比例函数 的图象在第_________象限内.
4.反比例函数 经过点(m,2),则m的值______.
5.反比例函数 的图象经过点(2,-3), 则它的表
达式为_______________.
双曲线
2
二、四
小结:反比列函数的图像所在的象限与系数 k有什么关系
当k>0时,两支曲线分别位于第一、三象限内;
当k<0时,两支曲线分别位于第二、四象限内.
在练习中回顾前面所学,自然地设疑,激发学生学习兴趣;
观察下列反比例函数的图象,回答下列问题:
(1)函数图象分别位于哪几个象限内?
第一、三象限内
x>0时,图象在第一象限;x<0 时,图象在第三象限。
在每一个象限内,y随x的增大而减小
(2)当x取什么值时,图象在第一象限?当x取什么值时,
图象在第三象限?
(3)在每个象限内,随着x值的增大,y的值怎样化?
如果k=-2, -4,-6,那么
的图象有又什么共同特征?
(1)函数图象分别位于哪个象限内?
x>0时,图象在第四象限;x<0 时,图象在第二象限
(2)在每个象限内,随着x值的增大,y的值怎样变化?
在每一个象限内,y随x的增大而增大
小结:
反比例函数的图象的位置与k有怎样关系?
当k>0时,两支曲线分别位于第一、三象限内,
在每一象限内,y的值随x值的增大而减小;
反比例函数的图象是双曲线
当k<0时,两支曲线分别位于第二、四象限内,
在每一象限内,y的值随x值的增大而增大.
在这个练习中,我引导学生结合观察图像,探索比较、发现规律:通过不同情况的比较,较全面的掌握反比例函数的性质。并进一步在小组中交流,在班上展示;本学段教法和学法遵循了有利于学生自主探索,动手实践、合作交流。学生通过观察、思考发现反比例函数的性质;我安排观察发现、分析归纳的发现学习法。
1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________.
(1)(2)(3)
(4)
随堂练习一
通过这一练习,初步检测学生掌握知识、运用知识的情况
2.若反比函数 图象位于第一、三象限,
则k的取值范围是_______________
k>-1
3.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )
C
在实际问题中
图象就可能只
有一支.
特别提醒
在前面练习的基础上,适当的引入学生最熟悉
的行程问题,提高了练习的难度和广度,进一
步提高学生运用知识解决问题的能力。
随堂练习二:
1.下列函数中,其图象位于第一、三象限的有__________;
在其所在的象限内,y随x的增大而增大的有___________.
2.(1) 已知点A(-2,y1),B(-1,y2),C(3,y3)都在反比例函数 的
图象上,比较y1、 y2 、y3的大小关系。
解:∵ k=4>0
∴ 图象在第一、三象限内,每一象限内y随x的增大而减小
∵ x1
点C(3,y3)在第一象限。
∴ y3>0, y2
(4)
本节练习注重学生明晰理由,
养成言之有理的严谨的数学学习习惯
通过这两节练习,是学生更好地理解知识,
运用知识,由易到难安排了两组练习,有
效拓展学生的知识面。
解:当k>0时, y2 < y1 < 0< y3.
当k<0时, y3 < 0 < y1 < y2.
(2)如果点A(-2,y1),B(-1,y2)和C(3,y3)都在反比例函数 的图象上,那么y1、 y2 、y3的大小关系又如何呢?
挑战自我:
学无止境,勇攀高峰
如图,已知过反比例函数 的图像上一点A
作 轴于点B,若三角形AOB的面积为2,
则K=_____________。
-2
在师生双边、学生多边的交流中,进行探究、合作、
创新,在努力完成挑战自我、勇攀高峰环节中,争取
大部分学生获得成就感,持续激发学生爱数学、用数
学的积极性。进一步激发学生自主探究与学习热情,
体会到学无止境,也较好的照顾了学习能力较强的学生。
观察反比例函数图象的两支曲线,回答下列问题:
(1)它们会与坐标轴相交吗?
(2)反比例函数的图象是中心对称图形吗?
(3)反比例函数的图象是轴对称图形吗?
它们都不与坐标轴相交。
是轴对称图形,它们有两条对称轴.
是中心对称图形,对称中心是坐标原点.
议一议
函数 正比例函数 反比例函数
表达式
图象
K>0
K<0
位置
增减性
位置
增减性
y=kx ( k≠0 )
( k是常数,k≠0 )
y =
x
k
直线
双曲线
在一三象限
y随x的增大而增大
经过一三象限
每个象限内, y随x的增大而减小
经过二四象限
在二四象限
y随x的增大而减小
每个象限内, y随x的增大而增大
填表分析正比例函数和反比例函数的区别
通过以上两个练习,学生在探索比较中发现规律,由此
自然地回顾本节课所学知识,并进一步通过横向比较,
总结正比例函数与反比例函数的异同,培养学生总结、
归纳知识的学习能力
1. 已知反比例函数 ,y随x的增
大而减小,求 的值和表达式.
提高练习:
O
x
y
A
C
O
x
y
D
x
y
o
O
x
y
B
D
1、反比例函数的性质: 反比例函数y=k/x的图象,当k>0时,图象位于第一、三象限,在每一象限内,y的值随x的增大而减小; 当k<0时,图象位于第二、四象限,y的值随x的增大而增大。
2、双曲线的两条分支逼近坐标轴但不可能与坐标轴相交。
3、反比例函数的图象是一个以原点为对称中心的中心对称图形。
4、在反比例函数y=k/x的图象上任取一点,分别作坐标轴的垂线(或平行线),与坐标轴所围成的S矩形=| k |
回顾与思考
回顾与反思,学生分组讨论、总结本节课所学的知识和技能。经过师生双边和学生多边的交流,使学生经历知识的形成与应用过程,达到学生所要掌握的基本知识与基本技能,发展应用数学的意义。
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
