苏科版数学八年级上册 4.1 平方根 教案(表格式)
文档属性
| 名称 | 苏科版数学八年级上册 4.1 平方根 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 62.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览

文档简介
4.1
平方根(1)
教学目标
1.了解平方根的概念,会用根号表示数的平方根;2.了解开方与乘方互为逆运算,会用平方根运算求某些非负数的平方根.
教学重点
了解开方与乘方互为逆运算,能熟练地用平方根求某些非负数的平方根.
教学难点
用平方根运算求某些非负数的平方根.
教学过程(教师)
学生活动
设计思路
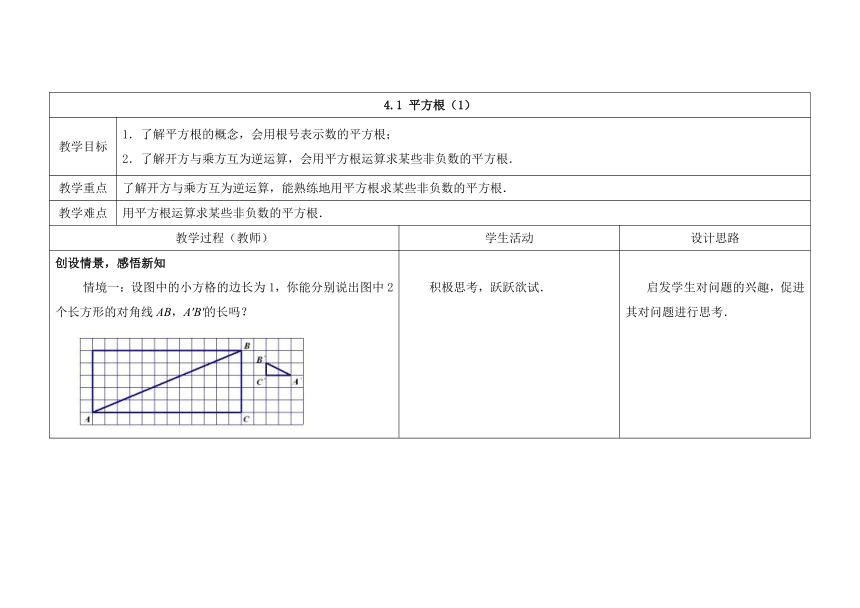
创设情景,感悟新知情境一:设图中的小方格的边长为1,你能分别说出图中2个长方形的对角线AB,A′B′的长吗?
积极思考,跃跃欲试.
启发学生对问题的兴趣,促进其对问题进行思考.
情境二:类似地,我们曾研究a2=2,那么a=?如果一个数的平方等于a,那么这个数叫做a的平方根,也称为二次方根.如果x2=a,那么x就叫做a的平方根,也称为二次方根.例如:2?=4,(-2)?=4,±2叫做4的平方根.10?=100,(-10)?=100,±10叫做100的平方根.13?=169,(-13)?=169,±13叫做169的平方根.一个正数的平方根有2个,它们互为相反数.一个正数a的正的平方根,记作“”,正数a的负的平方根记作“-”.这两个平方根合起来记作“±”,读作“正、负根号a”
.
思考、分析、讨论、交流.
让学生自己总结、交流,培养学生的概括能力和口头表达能力,培养自我反馈、自主发展的意识.
情境三:在下列各括号中能填写适当的数使等式成立吗?如果能,请填写;如果不能,请说明理由,并与同学交流.(
)2=9,(
)2=5,(
)2=;(
)2=0,(
)2=-,( )2=-4.
探索交流后总结出以下结论:一个正数的平方根有2个,它们互为相反数;0只有1个平方根,它是0本身;负数没有平方根.
通过对具体的数的平方根的讨论交流,使学生自己总结出正数、0、负数的平方根的情况,让学生经历探索规律的过程,加深对规律的理解.
例1 求下列各数的平方根.(1)25;(2);(3)15;(4)0.09.补充例题(可以选用).下列各数有平方根吗?如果有,写出它的平方根;如果没有,请说明理由.(1);(2).练习:课本95页练习.
分析:1.判断这些数是否都有平方根;2.根据规律各个数的平方根有几个?
在处理例题时要让学生充分参与分析,在运算时特别要注意一个正数的平方根有两个,对解题方式提醒应按要求.
总结1.说说你对平方根的理解.2.开平方运算与平方运算有什么联系?有什么区别?
尝试对知识方法进行归纳、提炼、总结,形成理性的认识,
内化数学的方法和经验.
试对所学知识进行反思、归纳和总结.会对知识进行提炼,体会数学的思想和应用,将感性的认识升华为理性的认识.
课后作业习题4.1第1题.
独立完成.
巩固所学知识.
平方根(1)
教学目标
1.了解平方根的概念,会用根号表示数的平方根;2.了解开方与乘方互为逆运算,会用平方根运算求某些非负数的平方根.
教学重点
了解开方与乘方互为逆运算,能熟练地用平方根求某些非负数的平方根.
教学难点
用平方根运算求某些非负数的平方根.
教学过程(教师)
学生活动
设计思路
创设情景,感悟新知情境一:设图中的小方格的边长为1,你能分别说出图中2个长方形的对角线AB,A′B′的长吗?
积极思考,跃跃欲试.
启发学生对问题的兴趣,促进其对问题进行思考.
情境二:类似地,我们曾研究a2=2,那么a=?如果一个数的平方等于a,那么这个数叫做a的平方根,也称为二次方根.如果x2=a,那么x就叫做a的平方根,也称为二次方根.例如:2?=4,(-2)?=4,±2叫做4的平方根.10?=100,(-10)?=100,±10叫做100的平方根.13?=169,(-13)?=169,±13叫做169的平方根.一个正数的平方根有2个,它们互为相反数.一个正数a的正的平方根,记作“”,正数a的负的平方根记作“-”.这两个平方根合起来记作“±”,读作“正、负根号a”
.
思考、分析、讨论、交流.
让学生自己总结、交流,培养学生的概括能力和口头表达能力,培养自我反馈、自主发展的意识.
情境三:在下列各括号中能填写适当的数使等式成立吗?如果能,请填写;如果不能,请说明理由,并与同学交流.(
)2=9,(
)2=5,(
)2=;(
)2=0,(
)2=-,( )2=-4.
探索交流后总结出以下结论:一个正数的平方根有2个,它们互为相反数;0只有1个平方根,它是0本身;负数没有平方根.
通过对具体的数的平方根的讨论交流,使学生自己总结出正数、0、负数的平方根的情况,让学生经历探索规律的过程,加深对规律的理解.
例1 求下列各数的平方根.(1)25;(2);(3)15;(4)0.09.补充例题(可以选用).下列各数有平方根吗?如果有,写出它的平方根;如果没有,请说明理由.(1);(2).练习:课本95页练习.
分析:1.判断这些数是否都有平方根;2.根据规律各个数的平方根有几个?
在处理例题时要让学生充分参与分析,在运算时特别要注意一个正数的平方根有两个,对解题方式提醒应按要求.
总结1.说说你对平方根的理解.2.开平方运算与平方运算有什么联系?有什么区别?
尝试对知识方法进行归纳、提炼、总结,形成理性的认识,
内化数学的方法和经验.
试对所学知识进行反思、归纳和总结.会对知识进行提炼,体会数学的思想和应用,将感性的认识升华为理性的认识.
课后作业习题4.1第1题.
独立完成.
巩固所学知识.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
